基于离散元的动载冲击地压巷道围岩稳定性分析

吴宏斌，刘 阳，王桂峰，刘心强，袁开源，李 庚

(1.华亭煤业集团有限责任公司陈家沟煤矿，甘肃 平凉 744100；2.中国矿业大学矿业工程学院，江苏 徐州 221116；3.煤炭资源与安全开采国家重点实验室，江苏 徐州 221116；4.徐州大月尔科技有限公司，江苏 徐州 221116)

冲击地压具有突然、急剧、猛烈等特点，是煤矿破坏性最为严重的动力灾害之一，易造成重大人员伤亡和采掘空间严重破坏[1]。我国每年都有巷道因动力破坏而造成人员伤亡的事故发生，严重制约着煤炭资源的安全高效开采。一次冲击能导致数十米到数百米范围的采掘空间突然破坏，造成人员伤亡和设备损坏。、近年来陆续发生的山东龙郓(2018年10月20日，死亡21人)、河北唐山(2019年8月2日、死亡7人)，山东龙堌(2020年2月22日，死亡4人)等数起严重冲击地压灾害，造成了严重的人员伤亡和重大的经济损失。

冲击地压多发生在巷道内，在冲击瞬间的灾变过程中，巷道围岩整体结构失稳破坏，并释放岩体积蓄的大量能量，巷道围岩快速挤向自由空间，是一种高能量、强冲击、短历时的突变性破坏。冲击产生的直接原因是巷道周边煤岩体中有能量积聚，采矿工程中的动载干扰可以诱发煤岩体中能量的突然释放。目前，采动动载诱发冲击地压现象正在逐渐被学者承认和接受，动载诱发冲击地压的机理和支护问题研究也在不断深入。

UDEC软件是岩土工程中常用模拟软件，能够有效地模拟出岩土工程中岩石静态或动态载荷下破坏的整个过程，利用UDEC软件的优势能够更好地模拟动载作用下巷道围岩的响应特征。对于采用离散元程序进行巷道围岩稳定性的研究，KANG等[2]采用UDEC软件分析了不同锚杆支护参数条件下的巷道围岩裂隙演化规律；方刚等[3]采用离散元程序UDEC软件中随机分布三角形单元块体集合模型研究巷道开挖失稳；马振乾等[4]采用离散元程序UDEC软件研究不同顶板软弱岩层厚度下巷道围岩能量演化规律，并提出基于能量平衡的巷道支护技术原理；张军等[5]结合峰前耗散能和峰后断裂能建立的脆性评价指数，能同时反映岩石脆性破坏的难易程度和脆性的强弱，可评价不同力学条件下的脆性变化特征；熊藤根等[6]采用有限元数值模拟FLAC3D软件对不同强度叠加动载作用下，巷道围岩应力、位移及塑性区分布规律进行了研究；陈治宇[7]采用离散元程序PFC动载作用下锚固体应力波传递规律及其力学响应特性进行了研究；刘学生[8]采用有限元数值模拟FLAC3D软件对动载作用下巷道围岩能置演化及冲击地压机理研究进行了研究。目前国内外对冲击地压防治方法的机理研究仍滞后于冲击地压防治的实践，因此对冲击地压等动力灾害机理及防治方法的研究仍是冲击地压动力灾害研究的长期目标[9]。

本文以陈家沟煤矿8514工作面为研究背景，借助离散元程序UDEC软件揭示动载作用下巷道围岩的响应特征，分析了不同距离动载对巷道稳定性的影响，研究成果可进一步揭示动载作用下巷道冲击破坏的机制，对开发相关防冲支护技术及指导现场安全生产具有重要的现实意义。

1 工程概况

8514工作面开采煤层为5#煤层(图1)，煤层厚度在24.6～35.8 m之间，平均厚度为27.8 m，煤层倾角在6°～14°之间，两顺槽均布置在5#煤层中下部，均按同一方位不同坡度送巷，运输顺槽全长2 327.7 m，开口底板标高为+939.24 m，顶煤厚度为8.2～19.2 m；回风顺槽全长2 281.1 m，开口底板标高为+941.15 m，顶煤厚度为9.45～16.20 m；工作面在可采范围内均为回风侧高于运输侧，工作面倾角在3.0°～16.5°之间，工作面设计平均长度为116.7 m。8514工作面开切眼与原8513工作面开切眼内错7 m，埋深为500～600 m，工作面开切眼与停采线之间的距离为2 143 m。

图1 8514工作面位置平面图Fig.1 Gateway layout of 8514 working face

8514工作面东部为8513综放工作面，区段之间保护煤柱宽度为6 m，8513综放工作面截至2020年4月底已回采1 952 m，剩余回采长度为235 m，由于地面村庄尚未搬迁，目前封闭管理。8514综放工作面南部为+930 m水平轨道大巷、+930 m水平胶带输送机大巷、+930 m水平回风大巷。8514工作面西部为八采区边界，与九采区相邻，保护煤柱宽度10 m。8514综放工作面北部为采区边界，与十采区相邻，保护煤柱宽度为10 m。8514工作面煤层顶底板情况见表1。

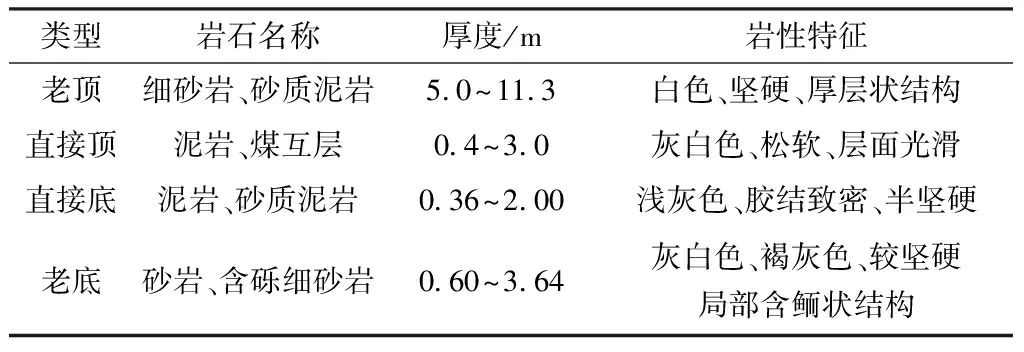
表1 煤层顶底板情况Table 1 Roof and floor condition of coal seam

2 数值计算模型的建立

2.1 模型建立

本文以陈家沟煤矿8514工作面为工程背景，通过现场观测、岩石样本取样获取岩石力学参数，并建立数值计算仿真模型。8514工作面运输顺槽设计断面为直墙圆弧拱形巷道，断面特征为净宽度5.2 m，净高度3.6 m，拱高度0.9 m，采用锚网索联合支护。

模型尺寸为长60 m，宽48 m(图2)，巷道断面为半圆拱形，在5#煤层中进行开挖，其断面参数为5.4 m×3.2 m。模型由泥质粉砂岩、粉砂岩、泥岩、5#煤层构成。静力计算模型左边界、右边界固定水平位移，底部边界固定垂直位移，按照地应力测试结果，顶部自由边界施加垂直应力均布载荷13.4 MPa，侧压系数x方向取1.20，z方向取1.74。为了更好地表现动载作用下巷道围岩变形特征，在5#煤层部分区域使用Voronoi多边形节理生成器，其他各个岩层则使用JSET统计节理生成器，节理模型如图3所示。

图2 UDEC模型Fig.2 UDEC model

2.2 模型参数选择

根据岩石力学试验结果，当载荷达到强度极限后，岩体产生破坏，在峰后塑性流动过程中，岩体残余强度随着变形发展逐渐减小[5]。因此，屈服准则采用Mohr-Coulomb强度准则判断岩体的破坏，计算公式见式(1)。

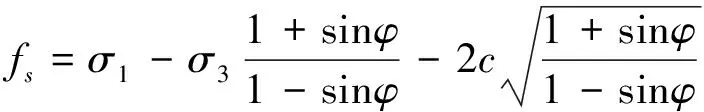
(1)

式中：σ1，σ3分别为最大主应力和最小主应力，Pa；c为内聚力，Pa；φ为内摩擦角，(°)。当fs>0时，岩体将发生剪切破坏。

根据现场地质调查和相关研究提供的煤岩体物理力学试验结果，模拟计算采用的煤岩体物理力学参数见表2。

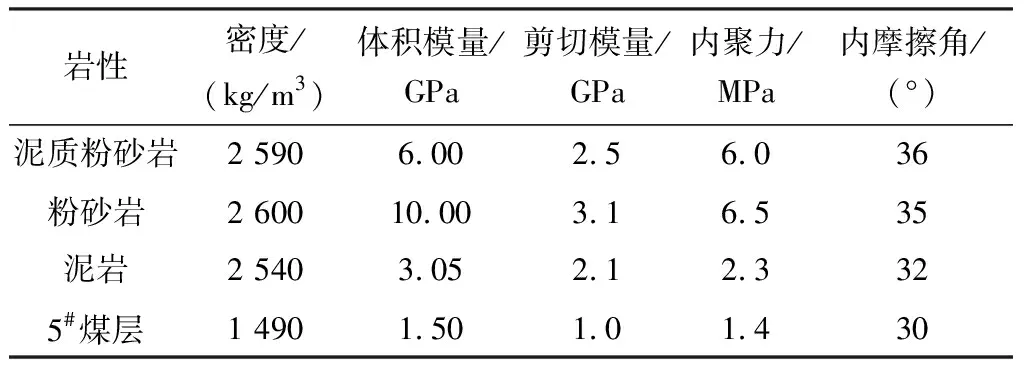
表2 UDEC数值模型岩层物理力学参数Table 2 Mechanical parameters of strata of UDEC model

2.3 动力荷载及边界条件确定

在动力分析时，由于计算模型采用有限体积来代替无限大的实际模型，在模型边界可能造成输入应力波的反射，影响计算结果的准确性。因此，模型采用黏弹性不反射边界，是一种人工边界，通过在边界上施加的切向阻尼和法向阻尼实现[10]。黏弹性人工边界具有精确度高、适应性好的优点，能够较为真实地呈现结构与周围介质之间的相互作用，在动力学相关的科学试验研究中得到了广泛的应用[11]。

震动在岩土体传播的过程能量会被消耗，如不考虑这部分的影响，则不能真实地模拟动对硐室结构的影响。 瑞利(Rayleigh)阻尼具有计算简单、适用性强等特点，一般常用于结构动力学研究分析，是常用的阻尼方式之一[12]。 模拟使用的离散元数值模拟软件UDEC以拉格朗日算法为基础，可以模拟块体之间的实际变形和位移。 UDEC软件包含强大的编程语言Fish函数，利用Fish函数，在进行模拟中可以对模型施加预期形式的应力波和控制应力波施加时间。

图4为计算模型边界条件示意图。模型四周均设为黏性不反射边界，计算中选取局部阻尼[13]。在巷道正上方的顶板煤层中施加动力扰动，用于模拟上方煤层开采时产生的应力波，动载作用时间取为0.02 s，输入的应力波采用余弦波[14]。

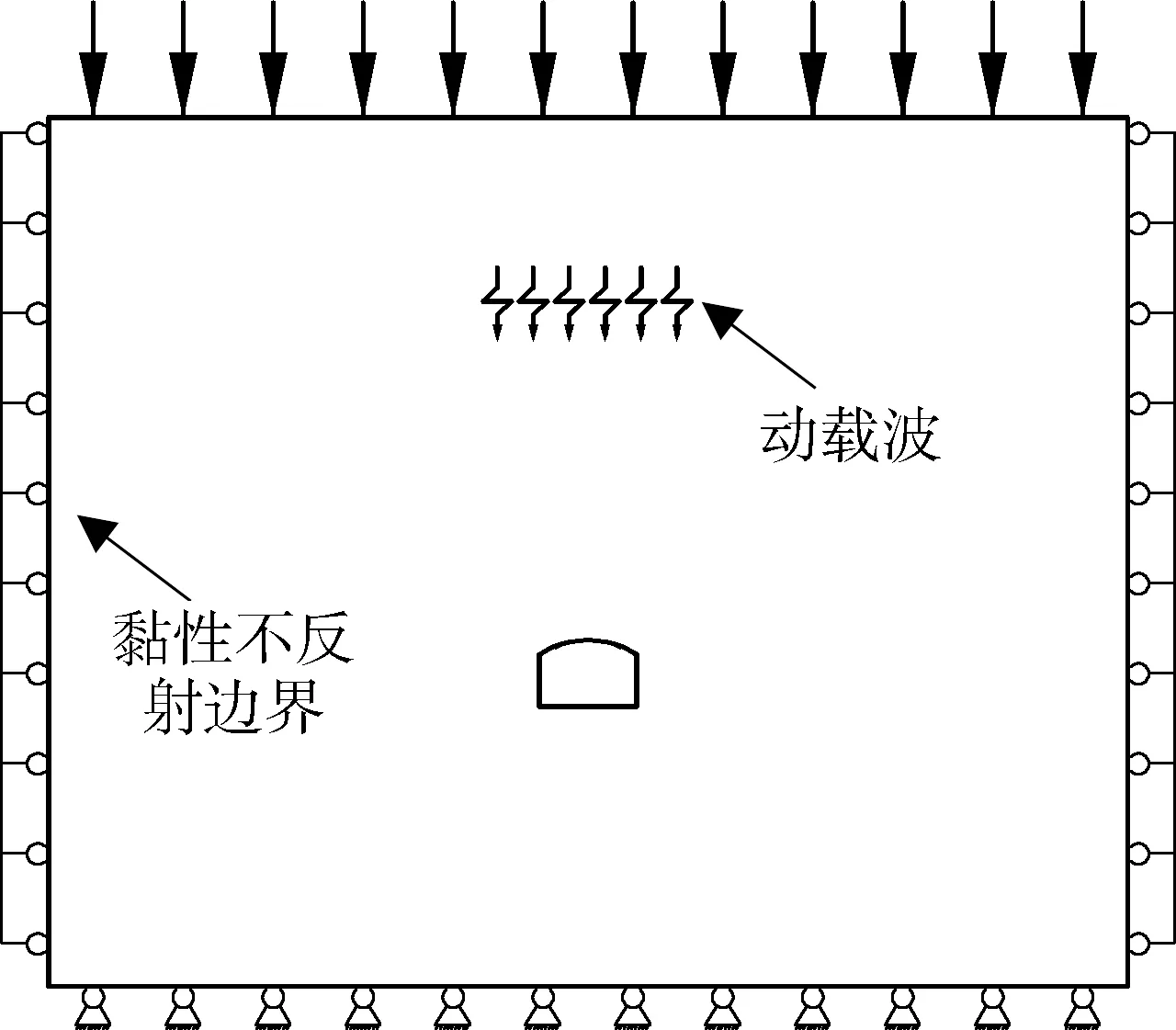
图4 数值模型动力计算边界Fig.4 Numerical model dynamic calculation boundary

3 模拟结果分析

数值计算模型在划分网格时对巷道周围20 m区域进行加密处理，可以使模拟结果更加精准，随后将模型在自重应力作用下计算至平衡，完成常规静力分析后，再对模型施加相关动载条件进行动力分析，静载模型运算平衡后，在距巷道顶部分别约10 m、20 m和30 m处10 m范围内分别施加振幅为5×104Pa的余弦波波形的动载，施加动载0.5 s后巷道周围应力分布情况如图5所示，动载施加后巷道四周中点的震动速度如图6所示。

图5 不同距离动载作用下巷道围岩的垂直应力演化规律Fig.5 Vertical-stress evolution law of surrounding rock under different distance dynamic load

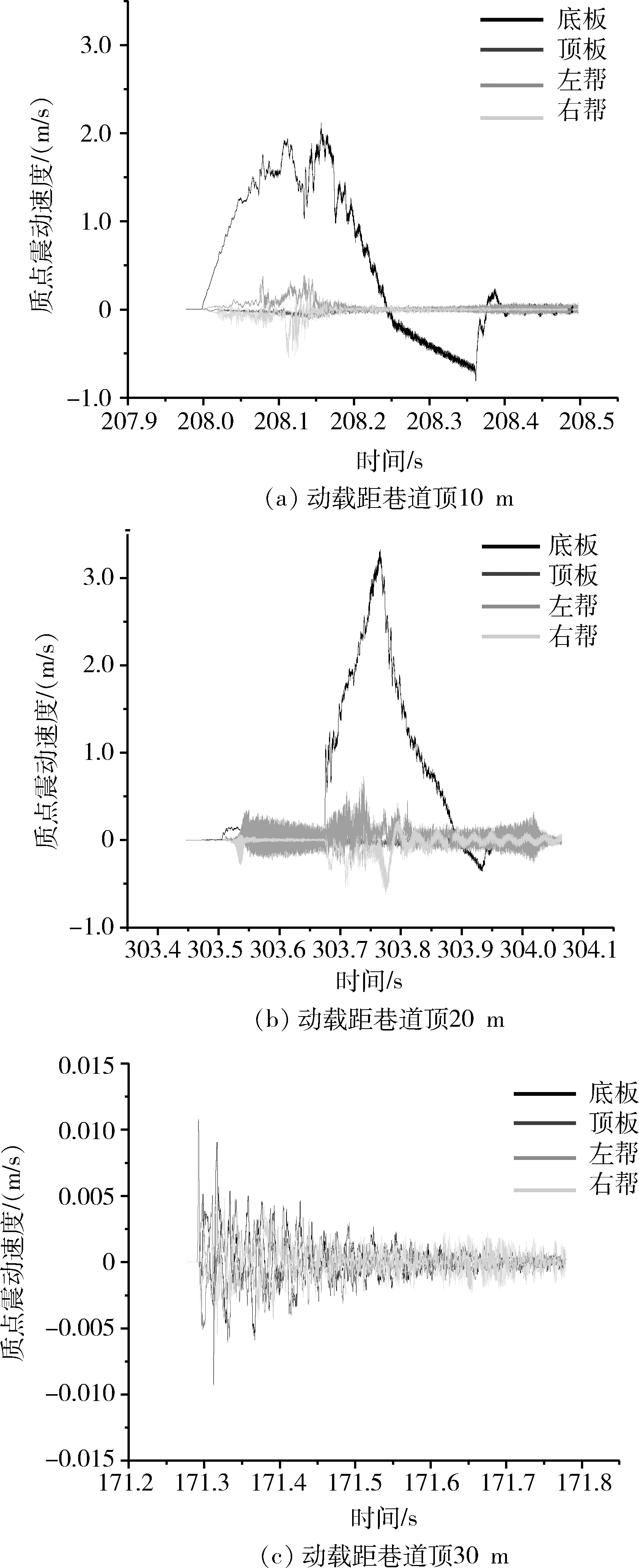
图6 不同距离动载作用下巷道震动速度演化规律Fig.6 Roadway vibration velocity evolution law underdifferent distance dynamic load

由图5可知，不同距离动载作用下巷道围岩的垂直应力演化规律。当动载距离巷道顶部为10 m时，巷道底板严重破坏，巷道顶板轻微破坏，巷道两帮基本无破坏，垂直应力在巷道两底角出现应力集中的情况，应力集中的范围较大；当动载距离巷道顶部为20 m时，巷道底板严重破坏，巷道顶板轻微破坏，巷道两帮基本无破坏，垂直应力在巷道两底角出现应力集中的情况，应力集中的范围较动载距离巷道顶部为10 m时有所减小；当动载距离巷道顶部为30 m时，巷道底板破坏情况较动载距离巷道顶部为10 m和20 m时明显改善，巷道顶板轻微破坏，巷道两帮基本无破坏，垂直应力在巷道两帮出现应力集中的情况，应力集中的范围较动载距离巷道顶部为10 m和20 m时有所增大，但应力集中强度明显减小。

由图6可知，不同距离动载作用下巷道围岩破坏范围及应力集中程度有明显变化，底板变形破坏范围会因动载与巷道顶部距离减小而增加，两者呈负相关关系。

对比图6可得出不同距离动载作用下巷道震动速度演化规律。巷道震动速度类似于正弦波的形式逐渐衰减并且存在峰值。动载距巷道顶部分别为10 m和20 m时，底板震动速度在动载作用下波动较大，出现突升，表征动力破坏，而顶板及两帮震动速度由于支护的存在，在动载作用下波动较小。动载距巷道顶部为30 m时，底板、顶板和两帮的震动速度波动峰值大小相近。

动载施加位置距离巷道顶板10 m和20 m时，巷道底板均发生了破坏。距离巷道顶板10 m时，自动载施加至巷道底板有明显变形破坏，约0.05 s；距离巷道顶板20 m时，自动载施加至巷道底板有明显变形破坏，大约0.25 s。动载施加后在巷道传播的过程中，受应力波影响区域的质点在应力波经过时因受外力扰动会发生震动，同时周围的应力环境也发生改变，应力波经过后，该区域的质点在一段时间内仍然会进行震动，随后才会逐渐降低，同时也反映出该区域应力会存在一段较为强烈调整的时间[15]。

由于巷道在动载作用下的破坏是突然发生的，运用离散元数值模拟软件UDEC进行模拟，巷道破坏时发生破坏的煤岩体之间的节理可以打开，煤岩体可以脱落并且弹射到巷道中，随之而来的是测点的质点震动速度会发生突然的升高并且会持续一段时间，此时一般代表着测点处的煤岩体在动载作用下已经脱离整体结构，也就是在动载作用下发生了冲击破坏。距离巷道顶板30 m时，自动载施加后底板一直保持完整状态，测点的震动速度就呈现出动载来到巷道附近时已经达到最大值，随后震动速度逐渐降低的形态。

4 结 论

本文利用离散单元法程序软件UDEC对动载作用下巷道围岩的响应特征展开系统研究，得到结论如下所述。

1) 随着施加动载距离的减小，在同样强度的动载应力波下，围岩裂隙扩展贯通更加充分，当达到一定程度后，引发巷道冲击动力灾害。因此，冲击地压的发生与动载荷的距离密切相关，这也是矿井在相同能量、不同距离矿震动载作用下显现情况不同的重要原因。

2) 动载距离巷道顶部分别为10 m、20 m时，底板震动速度在动载作用下出现突升，巷道发现动力破坏。 动载距巷道顶部为30 m时，巷道震动速度类似于正弦波的形式逐渐衰减并存在峰值。巷道底板破坏情况较动载距离巷道顶部为10 m和20 m时明显改善，巷道顶板轻微破坏，巷道两帮基本无破坏。

3) 距离巷道顶板20 m时，动载施加至巷道底板有明显变形破坏需约0.25 s。表明应力波经过巷道后，该区域的质点在一段时间内仍然会进行震动，随后才会逐渐降低，同时也反映出该区域在冲击破坏前应力会存在一段较为强烈调整的时间。