基于数值模拟正交试验的采空区稳定性因素的敏感性分析
2022-06-14何荣兴韩智勇邹开华
何荣兴,韩智勇,刘 洋,张 晶,邹开华
(1.东北大学资源与土木工程学院,辽宁 沈阳 110819;2.内蒙古科技大学矿业研究院,内蒙古 包头 014010)
地下矿产资源采出后形成采空区,采空区周围岩体的力学平衡被打破,在重力和次生应力作用下,会产生裂隙和变形。采空区的长期存在使一些矿区的地压活动加剧,相继从局部崩落发展到大范围的突然崩落,引起地表大范围的岩移,造成了严重的破坏。目前,采空区已成为金属非金属矿山安全生产的主要危险源[1],因此准确评估采空区稳定性状态,对于确定采空区处理方法和处理时机具有重要的指导意义。
目前,采空区稳定性评价方法主要有定性分析法、定量分析法、现场监测分析法等。采空区变形破坏总是在若干特定影响因素作用下产生的,而每一个影响因素又由若干因子组成,采空区稳定性受多种因素制约,各因素间又相互关联,决定了采空区稳定性评判是一个复杂的系统工程。因此,越来越多的学者采用数学方法对采空区稳定性进行综合评价[2-9]。在建立评价体系中,采空区稳定性因素的影响权重确定方法主要是专家打分法和1~9标度法,但二者均带有一定的主观性,影响采空区的评价结果。确定各影响因素的敏感性对确定复杂采空区失稳主控因素及相应的临界值并设计采场结构参数、为采空区稳定性综合评判体系构建过程中权重确定具有十分重要意义。国内外学者在此领域开展了大量研究工作。宋卫东等[10]从矿柱载荷、强度、失稳形式及影响因素四个方面推导出2种矿柱的安全系数计算公式,采用6因素、5水平正交试验分析矿柱稳定性影响因素的敏感性,并研究主要影响因素与矿柱安全系数之间的关系。 尹升华等[11]建立计算矩形矿柱安全系数的简化公式,采用正交极差分析对矿柱稳定性影响因素的敏感性进行评价,得到矿房宽度、矿柱宽度与矿柱安全系数间的关系曲线。随着计算机技术的发展,数值模拟在多方案理论研究方面具有明显优势,数值模拟已成为研究采空区稳定性的重要手段之一。王晓军等[12]利用FLAC3D软件完成多因素组合影响阶段矿柱上采过程数值模拟正交试验,分析了单一影响因素与顶板临界厚度的关系,利用多元非线性回归的数学方法,建立了上采过程3因素组合影响下顶板临界厚度数学预测公式。何标庆[13]利用FLAC3D软件对福建省某矿区大型采空区群的稳定性进行了模拟,结果表明采空区间柱多发生塑性破坏,采空区上下盘围岩存在冒落风险。彭超等[14]利用FLAC3D软件对某大理岩矿山采空区稳定性进行了模拟分析,结果表明采空区塑性破坏主要发生在顶板浅层围岩,采空区不会发生大规模失稳,并根据不同区域的稳定性制定相应的处理方案。
鉴于采空区稳定性受多因素影响的特点,本文综合各类岩体分级标准评价指标,能够反映岩体力学参数且容易量化的影响采空区稳定性因素,采用正交试验确定研究方案,利用霍克布朗准则,将各方案中的岩体质量指标转化了岩体力学参数,利用FLAC3D软件模拟分析影响采空区稳定性各因素的敏感性,对确定采空区稳定性评价的权重及矿山采场结构参数提供参考。
1 采空区稳定性影响因素分析及选取
影响采空区稳定性的因素较多,一般可概括为岩体质量因素、采空区规格参数和诱发因素三类。岩体质量是影响岩体稳定性的最基本因素,目前国际岩体分级标准包括Q分级[15-16]、RMR分级[17-18]、MRMR分级[19-20]以及《工程岩体分级标准》(GB/T 50218—2014),各分级标准所需的岩体质量因素见表1。不同分级标准的侧重点和选择岩体质量因素不尽相同,因此,本文选定的分析采空区稳定性影响因素能基本反映岩体质量,容易量化,而且通过这些因素可直接或间接估算出岩体的力学参数。点荷载强度或单轴抗压强度是反映岩体质量的重要指标,是大部分分级标准都不可缺少的,而且也是估算岩体力学参数的基础,二者具有良好的相关性,考虑到单轴抗压强度更加直接,因此选择岩石单轴抗压强度作为采空区稳定性的分析指标。岩石质量指标RQD、节理间距、岩体完整性系数、节理面产状、节理面条件等表征结构面特征的因素,存在相关性或是同一参数在不同方面的反映程度,根据上述原则选择岩石质量指标RQD、节理间距作为采空区稳定性因素进行分析。地下水对岩体工程稳定性和岩体本身强度具有重要影响,因此地下水因素在采空区稳定性分析中是不能忽略的。在已知节理面条件和产状的条件下,通过选定的上述因素即可获得岩体的RMR值即反映岩体质量,再利用Hoek-Brown强度准则便可估算出岩体的抗拉强度、内聚力、内摩擦角、弹性模量等力学参数。在模拟计算中还需要泊松比来确定水平应力大小和体积模量等参数,因此最终选择的影响采空区稳定性岩体质量因素包括单轴抗压强度、RQD、节理面间距、地下水、泊松比等5个参数。

表1 不同分级标准包含的岩体质量因素Table 1 Rock mass quality factors included in different grading standards
采空区稳定性很大程度上受采空区本身规格参数影响,主要包括采空区的高度、面积、埋藏深度、形状。生产实践中形成的采空区形状较为复杂,很难量化,为了便于分析量化,本文简化为规则采空区,用采空区的长宽比来定量表征采空区的形状。因此,在采空区规格参数中选择采空区的高度、面积、埋深、长宽比作为采空区稳定性评价因素。
实践表明,众多采空区灾害的发生,多是由于连续强降雨、山体滑坡、大规模爆破振动、采动扰动影响以及相邻采空区的影响等因素诱发的,可称为诱发因素,这些因素和采空区本身的稳定性无直接关系,且难于量化,因此本文不予考虑。
2 正交试验方案及力学参数估算
2.1 正交试验方案设计及数值模型建立
根据上述分析,本文选取9个因素,分别为单轴抗压强度、RQD、节理面间距、地下水、泊松比、采空区高度、采空区面积、采空区埋深和采空区的长宽比,并对各因素对空区稳定性影响程度进行分析。根据正交原则设计了“9因素4水平”的正交试验方案(表2)。利用FLAC3D软件建立各方案采空区模型,由于后续正交分析中要比较各方案的塑性区体积,为使结果具有可比性,建立模型时尽量使各模型采空区周围的围岩网格尺寸和密度保持一致,由于篇幅有限,只列出前4个方案的数值模型,如图1所示。

表2 正交试验方案Table 2 Orthogonal test scheme

图1 前四个方案模型图Fig.1 The simulation model of the four test schemes
对模型施加边界条件,模型底部采取铰支固定边界法,四周边界约束其横向位移,初始垂直应力为自重应力,根据模型尺寸以及方案中采空区的埋深,在模型顶部分别施加1.08 MPa、6.48 MPa、11.87 MPa和17.28 MPa的垂直应力,水平应力根据净水压力假设,计算公式见式(1)。
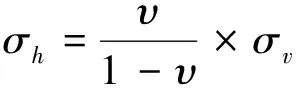
(1)
式中:σh、σv分别为围岩水平应力和垂直应力;v围岩泊松比。
本次数值计算将矿岩视作非线性弹塑性介质,采用莫尔-库伦准则作为屈服准则,其控制方程见式(2)。
(2)
式中:σ1、σ3分别为最大主应力和最小主应力;c、φ分别为材料黏聚力和内摩擦角;F为破坏判断系数,当F≥0时,材料将发生剪切破坏。
另外,材料在拉应力状态下,采用抗拉破坏强度准则。其力学模型见式(3)。
F=σt-Rt
(3)
式中:σt为材料所受拉应力;Rt为材料抗拉强度。如果拉应力超过材料抗拉强度(F≥0),材料将发生拉破坏。
2.2 岩体质量参数量化和力学参数估算
岩体质量参数对采空区稳定性的影响通过对围岩力学参数反映出来,因此各方案的岩体质量参数估算围岩的力学参数,不仅可将岩体质量参数量化,还可以为数值模拟采空区稳定性提供基础。目前,最常用的岩体参数估算方法是经验公式法,被广泛采用的方法主要有完整性系数(Kv)修正法、费森科法[21]、格吉法[22]以及霍克-布朗法[23]。 众多研究[24-25]认为Hoek-Brown强度准则比较全面地反映了岩体结构等特征对岩体强度的影响,是发展最完善的方法。Hoek-Brown岩体破坏准则表达式见式(4)。
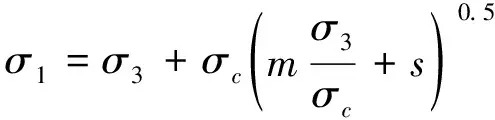
(4)
式中:σ1、σ3分别为岩体破坏时的最大主应力和最小主应力;m为岩体的Hoek-Brown常数;s为岩体材料性质的无量纲系数,m、s可用式(5)和式(6)估算。

(5)

(6)
式中:mi可根据不同类型岩体的Hoek-Brown常数表[20-21]来选取;RMR可根据岩石的强度、RQD值、节理间距以及地下水影响的综合评价岩体分类指标,其值可通过节理岩体的岩石力学分类(RMR)表计算得出[26-27]。
当σ1=0时,由式(4)可以得到岩体的抗拉强度,见式(7)。

(7)
Hoek-Brown给出岩体弹性模量Em与地质强度指标GSI的关系见式(8)。

(8)
式(8)可以用岩体分类指标RMR替代GSI值进行弹性模量估算。
Mohr-Coulomb强度准则认为岩体强度主要与岩体的内聚力c和内摩擦角φ有关,而最大主应力和最小主应力σ1、σ3之间存在线性关系,见式(9)。
σ1=σmc+kσ3
(9)

当0<σ3<0.25σc时,所做的三轴实验结果同时符合Hoek-Brown准则与Mohr-Coulomb准则,可由式(4)确定的不同σ1、σ3对式(9)回归得到岩体抗压强度σmc和k。
另外,岩体内摩擦角和内聚力可由式(10)和式(11)求解。
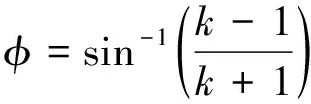
(10)
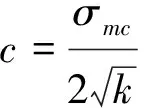
(11)
假设采空区围岩为石灰岩,节理面稍粗糙,宽度<1 mm,节理面岩石软弱,根据不同方案的岩体质量数据获得相应的RMR等相关参数,再利用Hoek-Brown准则便可估算出相应的力学参数,见表3。

表3 各试验方案的计算参数Table 3 Parameters of each test scheme
3 模拟结果分析
为了对表1的试验方案进行评价,需要制定评估指标。采空区围岩的塑性变形,可表征采空区失稳的开始,塑性区总体积的大小可评估采空区最终的稳定程度。不同采空区参数条件下,采空区顶板和边壁的塑性变形程度是不同的,有些采空区边壁岩体不断片帮导致最终采空区失稳,有些采空区失稳形式是顶板直接冒落,为评估采空区参数和失稳形式关系,顶板塑性区和边壁岩体塑性区可作为模拟结果的评估指标。因此,选择采空区塑性区总体积,顶板塑性区体积和边壁岩体塑性区体积作为各方案评估的指标。利用Fish语言编辑的塑性区体积查询小程序,可获得各方案的塑性体积,结果见表4。
对表4中的采空区模拟结果进行极差分析,结果见表5。其中,K1i、K2i和K3i分别为指标采空区顶板塑性区体积、采空区边壁塑性区体积和采空区围岩塑性区总体积在水平i下指标的偏差平均值(i=1、 2、 3、 4),Rj为对应三个指标的极差(j=1、2、3)。

表4 各试验方案的计算结果Table 4 Statistics of calculation results of each test scheme
通过极差计算得到的采空区顶板塑性区体积的影响因素敏感性主次顺序依次为:单轴抗压强度>采空区埋深>采空区面积>泊松比>涌水量>RQD>节理面间距>采空区长宽比>采空区高度;采空区边壁塑性区体积的影响因素敏感性主次顺序依次为:采空区埋深>采空区长宽比>单轴抗压强度>采空区高度>采空区面积>RQD>节理面间距>泊松比>涌水量;采空区塑性区总体积的影响因素敏感性主次顺序依次为:单轴抗压强度>采空区埋深>采空区面积>采空区高度>采空区长宽比>泊松比>节理面间距>RQD>涌水量。综合这3个指标可知,采空区埋深、采空区面积、单轴抗压强度、长宽比均排在前列,为进一步评估这4个因素随水平变化对采空区稳定性的影响趋势,将表5中各指标偏差的平均值,绘制成与对采空区敏感性最为敏感的4个因素、水平的关系趋势图,如图2~图4所示。各指标的偏差平均值大小与单轴抗压强度、采空区面积、采空区埋深和采空区长宽比因素水平变化呈曲线变化关系,采空区顶板塑性区体积偏差平均值随水平变化呈快速降低-缓慢减小或缓慢升高-快速上升的变化关系,边壁塑性区体积偏差平均值随水平变化呈先增加后降低的变化关系,围岩塑性区总体积偏差平均值随水平先变化近似呈线性增加或降低变化关系。总之,采空区埋深、采空区面积、单轴抗压强度、长宽比4个因素是对采空区稳定性影响最为敏感的,在评估采空区稳定性和设计矿房尺寸时,应将这4个因素作为重点因素。

续表4
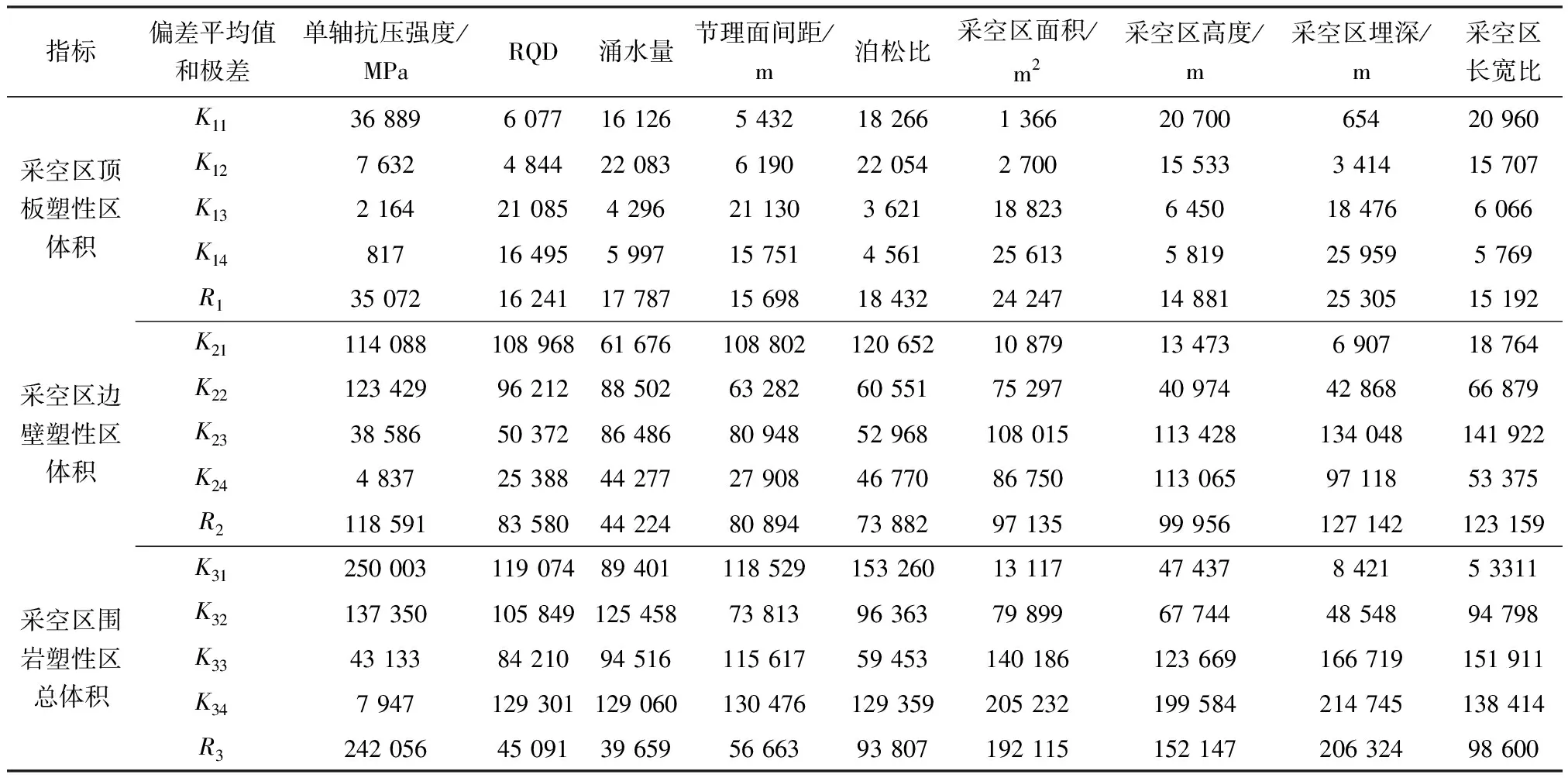
表5 各试验方案的极差分析Table 5 Extract analysis results of each test scheme
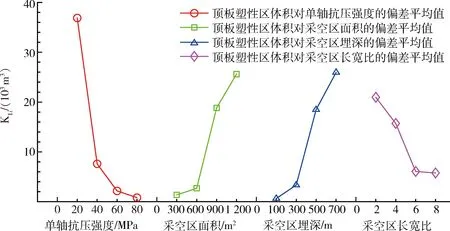
图2 顶板塑性区指标偏差平均值随因素和水平的变化趋势Fig.2 Trend of the deviation average value of volume of roof plastic zone along with factors and levels

图3 边壁塑性区指标偏差平均值随因素和水平的变化趋势Fig.3 Trend of the deviation average value of volume of sidewall plastic zone along with factors and levels
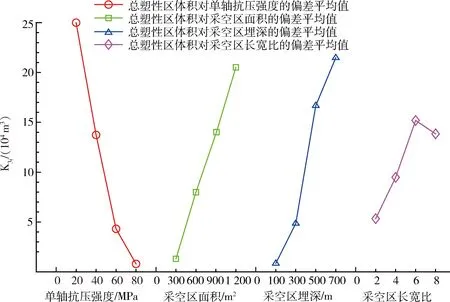
图4 总塑性区指标偏差平均值随因素和水平的变化趋势Fig.4 Trend of the deviation average value of volume of total plastic zone along with factors and levels
4 结 论
1) 在顶板塑性区体积,边壁塑性区体积和塑性区总体积评估指标下,各因素对采空区稳定性影响的敏感性不尽相同,根据不同指标下的因素敏感性顺序,采空区埋深、采空区面积、单轴抗压强度、长宽比4个因素是对采空区稳定性影响主要因素。
2) 采空区顶板塑性区体积偏差平均值随水平变化呈快速降低-缓慢减小或缓慢升高-快速上升的变化关系,边壁塑性区体积偏差平均值随水平变化呈先增加后降低的变化关系,围岩塑性区总体积偏差平均值随水平先变化近似呈线性增加或降低变化关系。
3) 对于具体矿山而言,岩体质量参数已固定,某一采深条件下的采场稳定性主要取决于采空区面积和长宽比,采场结构参数和稳定性也需要根据采深的变化进行动态评估。
