SA-PSO 混合算法的侧铣刀轴轨迹规划＊

韩军 姚晟

（内蒙古科技大学机械工程学院，内蒙古 包头 014010）

非可展直纹面由于其原理性误差的存在，数控加工难度大，所以不断减少加工误差成为学者们的研究焦点。Liu X W[1]等提出柱刀的单点偏置法，但会造成单一的欠切或者过切误差；严涛[2]等利用四点偏置法确定初始刀轴的位置，通过刀具包络面逼近非可展直纹面为优化目标，利用最小二乘法进行优化，一定程度上减小了过切误差；宫虎[3]等提等距面的概念，使得计算过程更加简便；阎长罡[4]等对圆锥刀侧铣加工非可展直纹面，提出一种基于粒子群优化算法的解决方案，该算法属于智能算法，对比于之前学者研究，该方法显著降低了包络面与设计曲面的误差；孔森[5]等提出基于MWOA 算法，利用鲸鱼算法通过引入扰动因子来不断更新适应度值较差的因子，取得较为理想的仿真效果。

模拟退火算法是一种随机寻优算法，源于固体退火过程[6]。固体退火是先将固体加热到一定温度，再使固体温度慢慢下降，使固体内部粒子排布更均匀，从而改变固体性质的过程。模拟退火算法首先规定一个初始温度,随着温度不断下降，在每一个温度停留并接受新值，结合概率突跳性不断寻优。模拟退火算法能越过当前最优值从而找到全局最优解，需要的解空间较多，局部搜索能力弱，迭代次数多。

粒子群算法源于鸟类觅食行为[7]。根据鸟类具体位置分布，在寻找食物时分享自身找到的食物信息，通过自身的信息共享使得整个鸟群找到食物最多的地方即最优解。粒子群算法简单、参数少以及收敛速度快，但容易陷入局部极值。

结合两种算法的优点，对圆柱刀刀具包络面逼近设计曲面求解最优刀轴位置。首先利用三点偏置法确定初始刀轴位置姿态，其次建立一个初始刀位下的误差判定函数，然后对初始刀轴位置进行初始种群的生成，最后利用模拟退火算法和粒子群混合算法进行刀轴位置寻优，寻找出单刀位下的最优位置。利用优化后的刀轴位置获得刀轴轨迹面[8]，进而计算得出包络误差。通过实际加工比较PSO 与SA-PSO 的效果。

1 初始刀位生成

直纹面包括2 种参数线 (u,v)，其中u线为导线，v线为直母线，直纹面为一条直线u，沿着任意轨迹曲线v生成的曲面。其方程可表述为

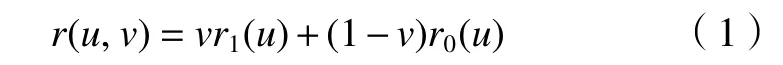
将2条导线r0(u)和r1(u)统称为r(u)，设 τ(u) 为ρ(u)点处的单位方向矢量，则直纹面r(u,v)还可表示为

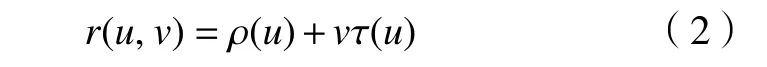
根据式（2）可得直纹面r(u,v)上任意一点的法矢为nr(u,v)，方向与如下矢量平行。

采用三点偏置法建立初始刀具位置姿态，图1为初始刀轴位置。

图1 初始刀轴位置

2 误差判定函数的建立

非可展直纹面同一母线上的法向矢量方向不同，当刀具直径大于0 时，无法使刀具滚动形成的包络面完全贴合设计曲面，这就导致在刀具加工时,会没有接触到设计曲面或者嵌入到设计曲面里面,称为非可展直纹面的原理性误差。将刀轴离散化,设Q为刀轴上一点，记在刀轴上所有的离散点的集合为Q1,Q2,Q3,···,Qn,n∈[1,+∞)为离散点采样点数。过Q1,Q2,Q3,···,Qn向设计曲面做垂线，垂足记为P1,P2,P3,···,Pn,垂足点记为 (ui,vi)。

假设所有刀轴位姿都处于最优位置，即设计曲面与包络面完全贴合，那么在每一刀轴位姿下必有

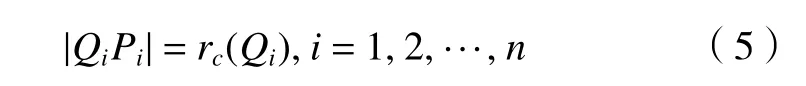
式中：|QiPi|表示刀轴不同位置点到设计曲面的距离；rc(Qi)为刀轴上不同位置点的刀具半径。

但实际情况是，由于原理性误差的存在，刀具切向设计曲面时，会有不同程度的欠切或者过切误差，这就导致理想最优位置无法实现，即||QiPi|-rc(Qi)|总大于零。所以在这种情况下，只能将问题转化为求||QiPi|-rc(Qi)|的极小值问题。若在每一单刀位情况下，||QiPi|-rc(Qi)|都为最小值，那么刀具切削时产生的包络面会无限逼近设计曲面,则原理性误差会降到最小。

根据上述分析,得出误差度量函数为

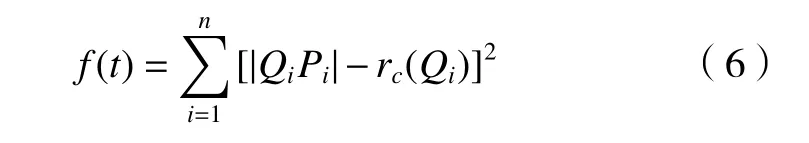
最优刀具位置姿态应是刀轴任意一点到设计曲面的距离与到刀具表面的距离平方和最小。刀具半径rc(Qi)确 定，因此问题就转化为求解 |QiPi|（刀轴一点到设计曲面的距离）。刀轴上任意一点作垂线到设计曲面上的垂足点 (ui,vi)满足以下方程

式中：ru(ui,vi)为 刀轴一点Qi在u方向的切向矢量；rv(ui,vi)为 刀轴一点在v方向的切向矢量。

式（6）实际上就是求解一个函数极小值问题，误差度量函数在现有条件下无法确定显性的函数表达式，传统方法难以进行求解，而智能算法在这方面具有显著优势。

传统方法的缺点在于只能计算单个刀具位姿在某一位置与设计曲面的位置关系，判断在这一位置是处于欠切或过切；只能使包络面精度更好地逼近设计曲面，却无法寻找到最优位置，并且计算过程复杂耗时。智能算法只需在MATLAB 中搭建曲面和刀具的数学模型，利用SA-PSO 算法对图2 中所生成的球型区域范围进行粒子寻优，随机两个粒子进行刀轴的生成，利用刀轴上给定的离散点多次调用误差度量函数进行误差判别，无需进行复杂的计算，耗时短，搜索范围大，精确度高。

图2 初始种群生成图

3 基于SA-PSO 混合算法的刀位优化

3.1 初始种群的生成

如图2 所示为最初样本种群生成图。图中两圆球是以刀具轴线两端点A0′和A1′为球心，R为半径生成。随机连接两个球体的各个位置，得到随机线段作为初始刀轴位置，重复上述步骤，可在Matlab 中生成一个群体总的数量为G的刀轴矢量数组，记为K[0],K[1],K[2],···,K[G-1]。设刀轴矢量的两端点A0′和A1′坐标分别为 (X0,Y0,Z0)和 (Xn,Yn,Zn)，对于每一矢量数组K，一对粒子的共有6 个矢量坐标，共计G个6 维矢量作为混合算法的初始种群。

3.2 基于SA-PSO 算法的优化流程

模拟退火算法的核心是蒙特卡洛判断准则，判断接受当前最小值公式为

式中：M为接受新解的概率。根据式（8）可得,当新值小于当前值时，必定接受新值；当新值大于当前值时，有一定概率被接受；当降温系数h和初始温度T不变时，新值超过当前值越多，那么新解被接受的概率越小。SA 的核心在于：不强制要求最新产生的解优于当前解。由于这种概念的引入，使得其避免产生群体粒子收敛速度过快而导致的无法获得全局最优解的问题，显示了其容易跳出局部极值的优越性。粒子群算法基于社会信息共享，通过比较当前自身适应度值与历史最好适应度值；比较当前适应度值与全局最佳适应度值，达到快速收敛的目的，但容易出现后期收敛速度过快导致迭代停滞的情况。本文通过SA-PSO 混合算法，先利用SA 算法的全局收敛性，再利用粒子群算法局部收敛速度快的特性找到最优刀轴位置。SA-PSO 算法的流程图如图3 所示。

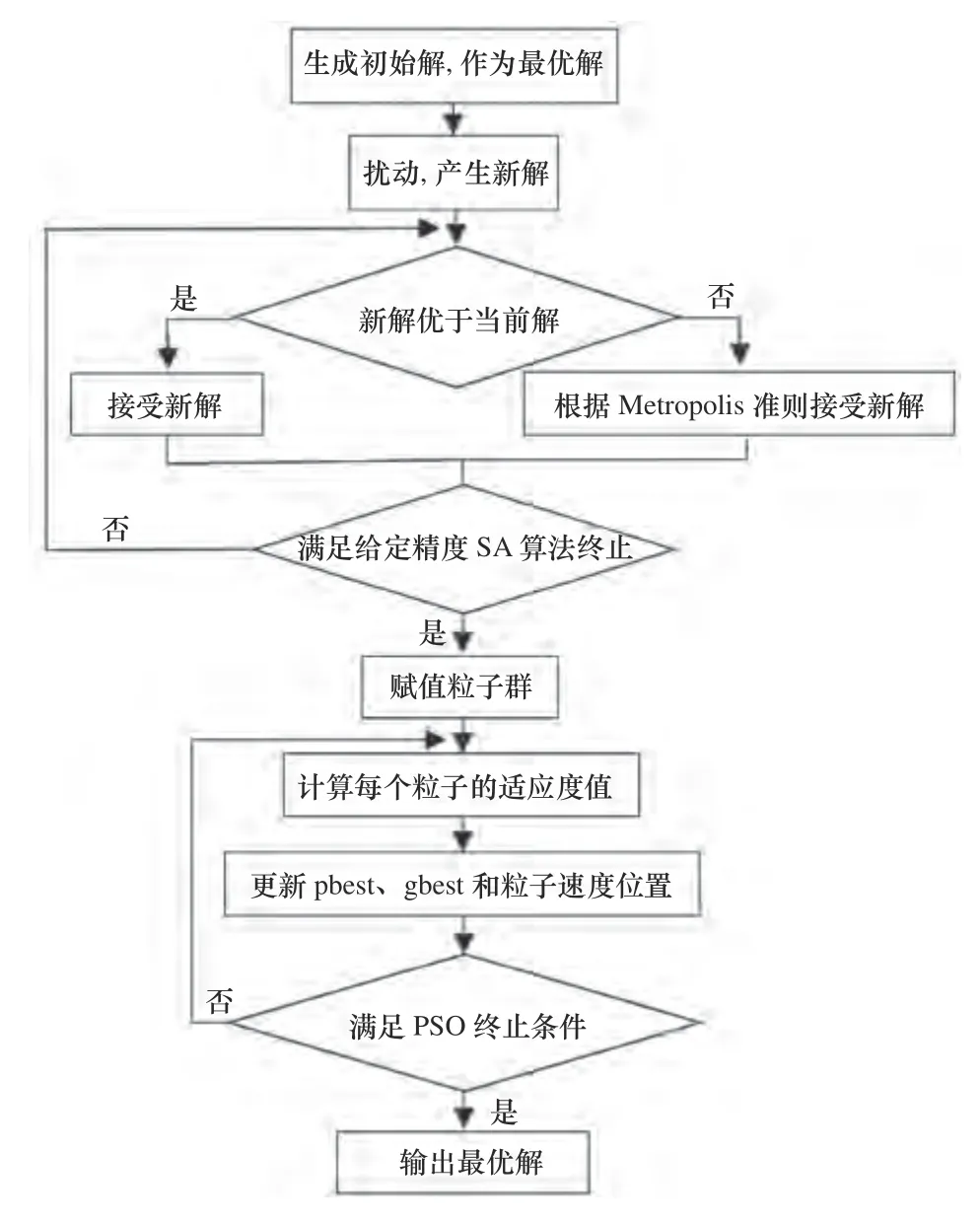
图3 SA-PSO 算法流程图

设计步骤如下：

（1）生成初始解。赋予种群粒子初始温度为T、马尔科夫链的长度，即等温过程的迭代次数L、温度下降速率h、算法终止温度TN和初始解x0。

（2）产生新解与当前解的差值。根据当前解xi进行扰动，产生一个新解xj，计算出相应的函数值E(xj)，得到 ΔE=E(xj)-E(xi)。

（3）判断新解是否被接受。若 ΔE＜0，则新解被接受；若 ΔE＞0，则新解按概率进行判断，Ti为当前温度。

（4）算法终止条件。当模拟退火算法达到给定精度时停止迭代，终止条件为

式中：ε为一个足够小的正数。

（5）赋值粒子群。将模拟退火算法算出的最优值赋值给粒子群。

（6）计算每个粒子的适应度值。将当前适应度值与历史最佳值比较，并跟新pbest。

（7）粒子位置状态更新。粒子在d维空间的速度和位置分别如下所示。

（8）重复步骤（6），再将pbest与群体最优位置离子gbest进行比较，若pbest的位置更优，则更新gbest。

（9）重复上述（7）和（8），达到迭代次数时停止计算并输出gbest。

4 包络误差的计算

4.1 圆柱刀侧铣刀具包络面误差

如图4 所示S为加工所形成的刀具包络面，S(u,v)为设计曲面，S1和S2为设计曲面S(u,v)的内外等距面，S1S2构成的包容域范围包括S1S(u,v)和S2S(u,v)两 部分。S1S(u,v)表示过切误差,即刀具加工过切部分；S2S(u,v)为欠切误差，即刀具没有加工到的部分。包络面误差即刀具包络面S无限逼近设计曲面S(u,v)时的误差。整体优化的目标就是保证包容域范围S1S2即ε极差最小。

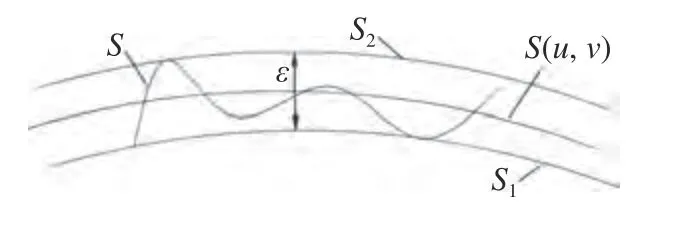
图4 圆柱刀侧铣包络误差图

4.2 侧铣加工误差计算

如图5 所示，过刀轴A'点向刀具侧壁和设计曲面S(u,v)做垂线，分别得到A点和B点，并延长A'B与刀具侧壁交于C点，B点为刀轴上A'点在设计曲面的映射点。线段BC为加工误差，当A'C＞A'B时，刀具与设计曲面过切；当A'C＜A'B时，刀具与设计曲面欠切。由上述可得刀位上某点处的误差方程为

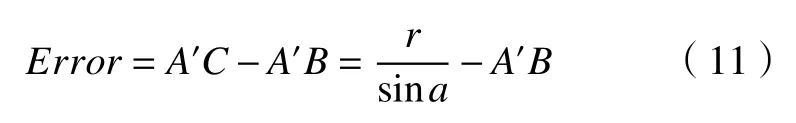
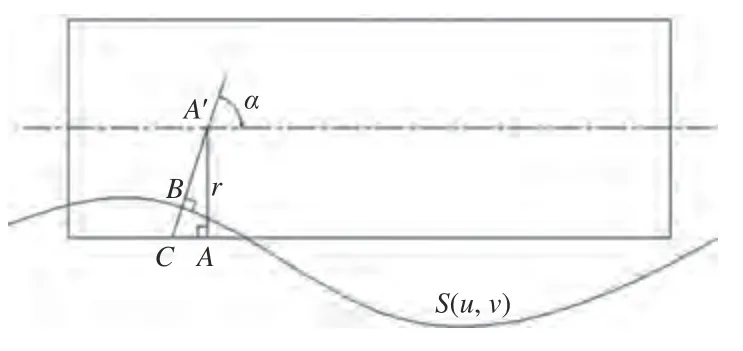
图5 侧铣加工误差计算

设计曲面为非可展直纹面，在加工阶段，刀轴上不同位置点在设计曲面的垂直点不断变化，其对应点的法向量也在做出相应变化，因此这里采用数值法进行求解[9]，具体方法是：在MATLAB 搭建的设计曲面和刀具数学模型中根据第三节内容：刀轴上的给定离散点Qn向设计曲面S(u,v)作 垂足点Pn。具体操作对应图5从A'点向设计曲面S(u,v)作的点B。利用MATLAB 进行数值计算，先确定从A'点向设计曲面作的垂足点B的具体坐标，并延长与刀具表面交于点C，这样点C的坐标也得以确定。点B和点C的坐标已知，包络误差就为BC之间的距离，可计算出包络误差的具体大小。通过判断点C在设计曲面的上方还是下方确定包络误差的正负值,正值为欠切,负值为过切。

5 对比仿真与分析

本文叶片原始数据来源于某企业整体式叶轮，将单个叶片划分为10 个叶面片体，选取第2 个区面片体为例。参数u和v分别为曲面片体的导线和母线。在第2 个曲面片体u方向上均匀选8 个刀位，在v方向的8 个刀位上，每个刀位均匀选取8 个点位作为误差度量的判断点。采用直径为6 mm 的柱刀进行仿真。叶片曲面如图2 所示。顶部导线和底部导线控制点如表1 所示。

表1 b 样条曲线控制点

在u=0处进行误差函数迭代的计算，计算结果如表2 所示。其中第3 次迭代优化结果最优。当在u其他位置时结果与其相似。

表2 单刀位误差函数优化

图6 为SA-PSO 的迭代图，SA-PSO 算法的种群数目为50，规定最大迭代次数为100 次。如图所示在第34 次迭代时，曲线趋于平缓。

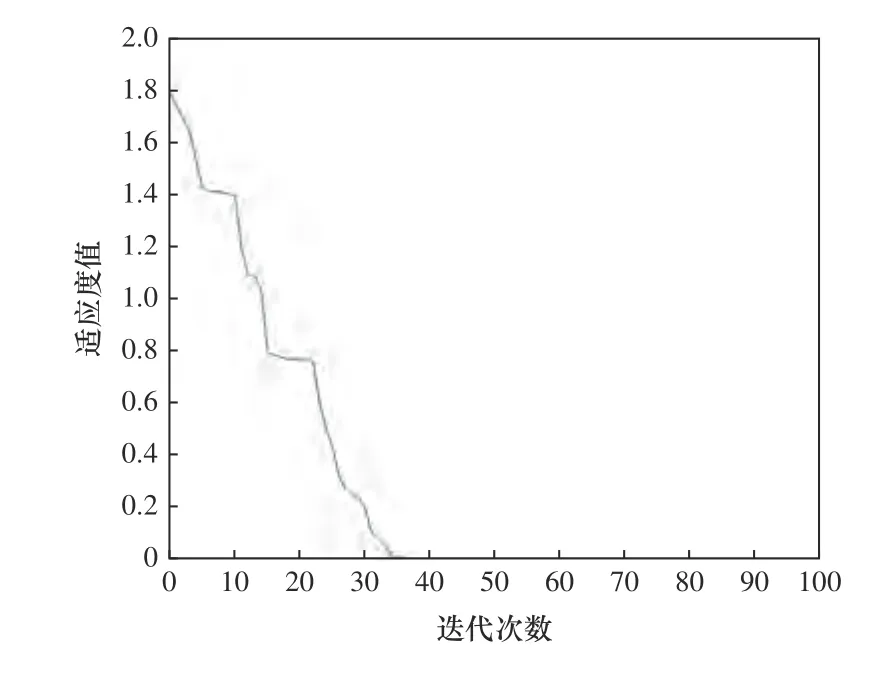
图6 单刀位优化迭代图

图7 为刀具初始位置的包络误差图，在初始位置时，包络误差范围在-0.5～0 mm，刀具与设计曲面呈过切状态。

图7 初始包络误差图

图8 为经PSO 算法优化后的包络误差图和经SA-PSO 算法优化后的包络误差图。图8a 包络误差范围在-0.015～0.015 mm，图8b 包络误差范围在-0.01～0.01 mm。两种算法优化后的刀具和设计曲面之间的关系都呈欠切和过切相间分布，且SA-PSO算法误差值明显较单一的PSO 算法有所减小。

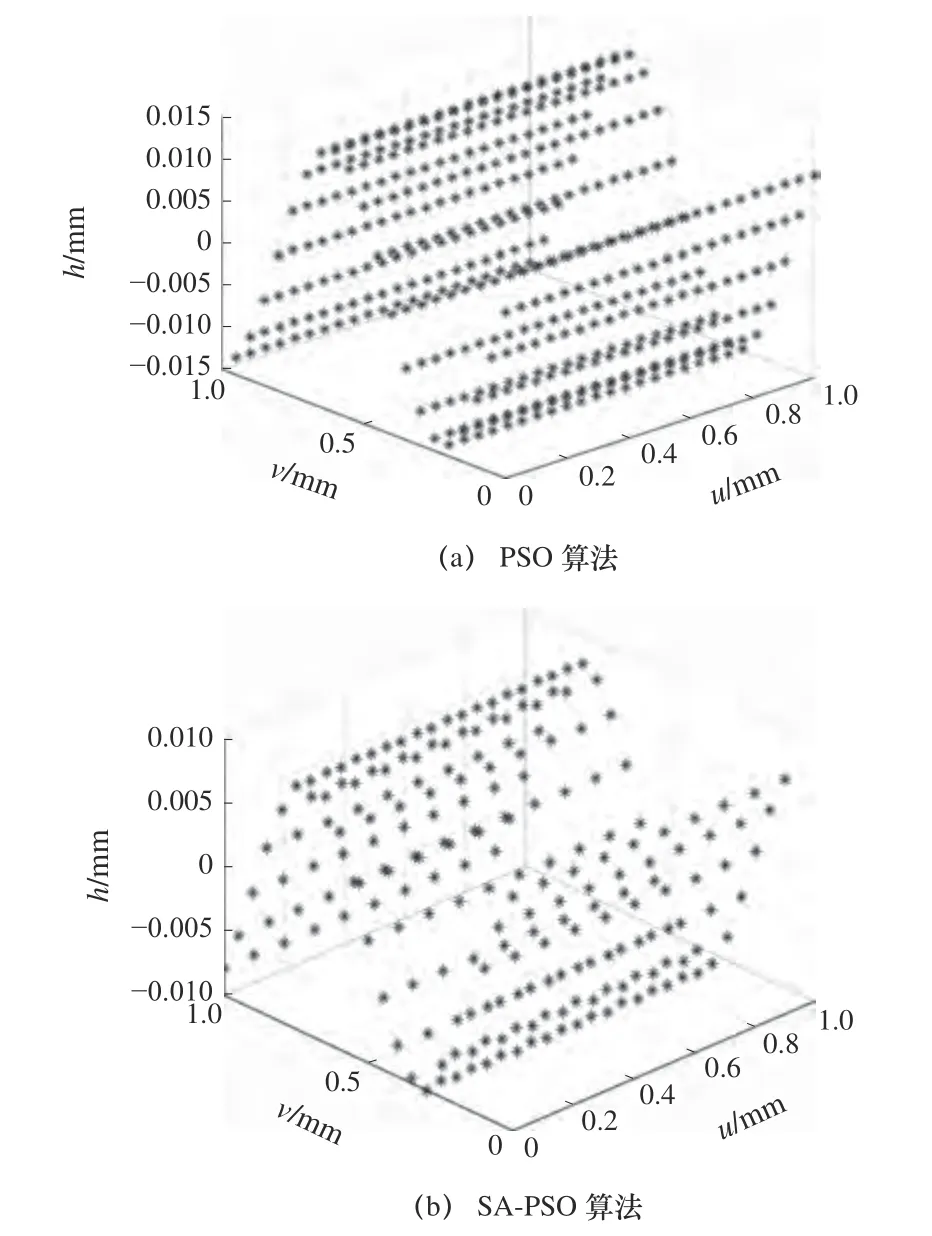
图8 包络误差图

图9 为包络误差对比示意图。图9a 为初始刀轴包络误差，呈过切分布；图9b 为算法优化后的包络误差图，呈过切和欠切相间分布，对比于初始误差减小很多。

图9 包络误差对比示意图

表3 为在PSO 和SA-PSO 算法的包络误差值。从表中可以看出，当计算到第七次时，两种算法的都达到最优解，即极差值最小，分别为0.021 3 mm和0.016 9 mm。对比于单一的粒子群算法，混合算法的极差均值减小了14.7%。

表3 包络误差值 mm

表4 和表5 分别为初始刀轴轨迹面和经SA-PSO优化后的刀轴轨迹面。

表4 初始刀轴轨迹坐标

表5 优化后的刀轴轨迹坐标

仿真结果表明，SA-PSO 算法较于PSO 算法在包络误差方面有较大的精度提升。

6 实验加工和结果分析

在型号为HS5AXIS 350 的五轴机床上进行整体式叶轮加工。机床和加工过程分别如图10 和11 所示。

图10 实验加工机床图

图11 加工过程图

刀具的选择极为重要，表6 为刀具参数表，其中T3 刀具的选择与仿真加工的刀具一致。

表6 刀具参数

整体式叶轮加工工序分为粗加工、半精加工和精加工，需更换4 把刀具。表7 为数控加工工序表。

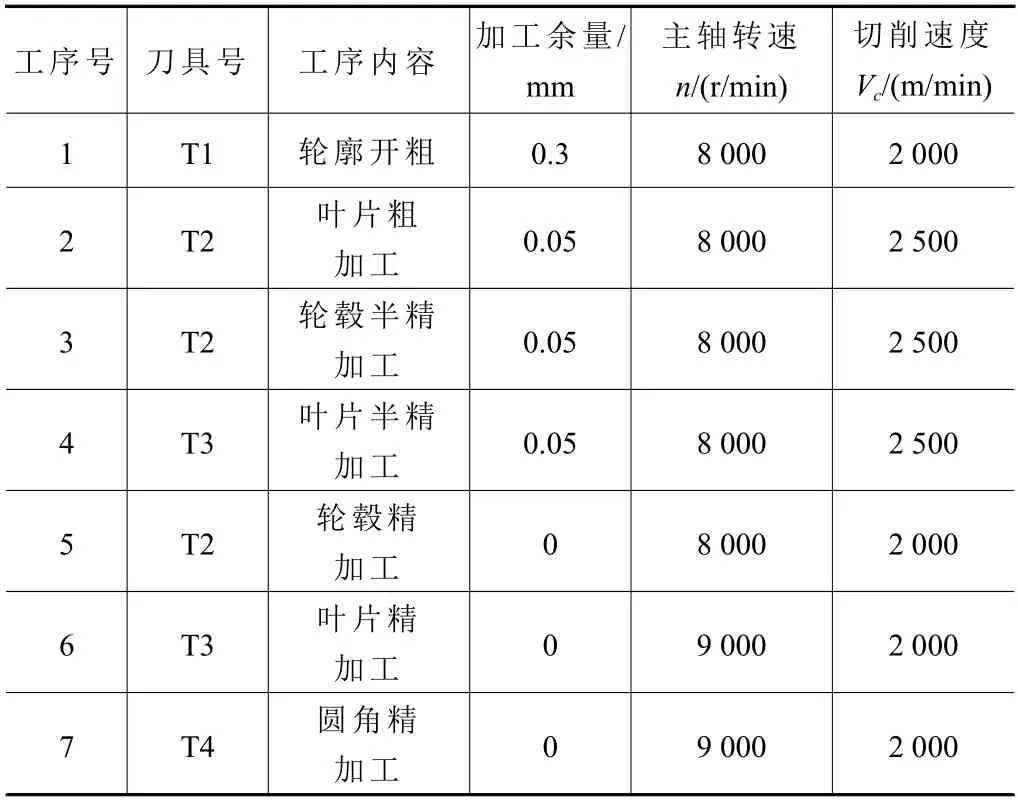
表7 数控加工工序表

图12 为叶片侧面加工比较图，图12a 为PSO算法加工，图12b 为SA-PSO 算法加工。对表7 中步骤6 即精加工后的叶片，利用图13 中的三坐标测量仪进行检测，分别选取两种算法精加工完成的叶片（表7 中步骤6）表面上与仿真位置相同的8×8 个点进行实际坐标测量，并与仿真结果所呈现坐标进行对比计算。

图12 叶片侧面加工比较图

图13 坐标测量图

将两种算法的实际加工误差进行坐标误差计算，得到如图14 所示的实际加工误差比较图。横坐标表示8 个刀位，纵坐标表示每个刀位上8 个点的误差极差值，共计8×8 个点。从图中可以看出在实际加工中，PSO 算法和SA-PSO 算法的极差值普遍大于表3 中仿真的极差值，表明实际加工与理想加工有一定的误差。但SA-PSO 算法实物加工误差比PSO 算法加工误差的绝对值更接近于0，表明SAPSO 算法的加工误差更小。

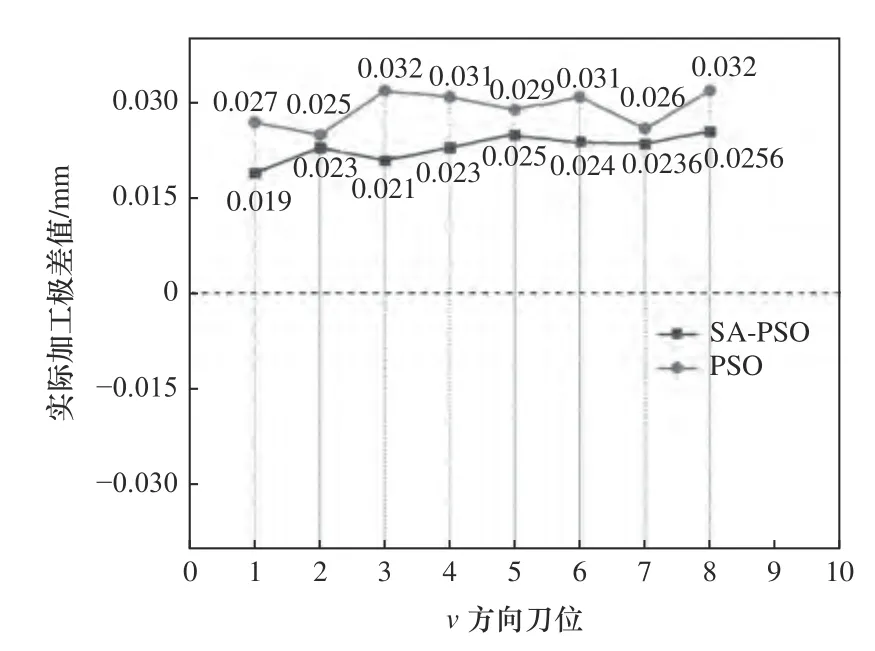
图14 实际加工误差比较图

7 结语

通过计算SA 算法和SA-PSO 混合算法的包络误差，得出在仿真加工同一非可展直纹面时SA-PSO算法比PSO 算法的包络误差的极差均值减小了14.7%；实验加工和理论值存在一定误差，但仍能为五轴侧铣加工非可展直纹面提供一定的参考价值。未来研究将考虑一定的物理因素，如铣削力、刀具刚度等。同时混合算法的提出为解决非可展直纹面加工的问题提供了新的思路。