基于参数不确定性条件下的齿轮弯曲疲劳可靠性灵敏度分析＊

2022-06-13李明凯康贺铭李永平杨溥陈雨于欢邓海龙

制造技术与机床 2022年6期

李明凯康贺铭李永平杨溥陈雨于欢邓海龙②

（①内蒙古工业大学机械工程学院，内蒙古呼和浩特 010051；②内蒙古自治区先进制造技术重点实验室，内蒙古呼和浩特 010051）

齿轮作为机械传动中应用最广泛的一种传动形式[1]，在采矿工程、装备制造、交通运输以及航空航天等诸多领域占据着重要地位。然而，受重载、高温等恶劣工况的影响，齿面点蚀、齿根断裂等齿轮疲劳失效问题时有发生，从而导致整体传动系统的精度波动、运行失稳以及可靠性降低，而在运行周期为高周乃至超高周等疲劳领域尤为显著。实际工况中，齿轮齿根弯曲应力主要导致弯曲疲劳失效，较大的齿面接触应力主要导致接触疲劳失效[2-3]；齿轮弯曲疲劳失效约占齿轮疲劳失效的1/3[4-5]。为了更为全面地评估齿轮弯曲疲劳可靠度指标以及更好地把握不同参数对齿轮弯曲疲劳的影响规律，对齿轮弯曲疲劳开展基于不确定条件下的可靠性灵敏度分析具有重要意义。

目前，众多国内外学者对齿轮弯曲疲劳可靠性进行了深入研究，并由此产生了一系列的相关理论和方法。赵永翔等[6]基于标准和可靠性曲线，分析并确定了HXDIC 大功率机车传动齿轮的抗弯疲劳强度、寿命和可靠性水平；Zhang J等[7]通过稳健性理论和方法，建立了基于齿轮接触寿命参数和弯曲强度的可靠性模型，并考虑了不可避免的强度退化因素；安宗文等[8]对风电齿轮箱中的某从动轮的接触疲劳和弯曲疲劳失效分别进行了可靠性灵敏度分析，分别确定了影响齿轮接触疲劳与弯曲疲劳可靠性的最大参数；候志林等[9]通过仿真手段，对CRHBX 型动车组体进行有限元分析，获得了影响可靠性的随机变量参数，并计算得出多失效模式下的各参数可靠性灵敏度；张艳林等[10]采用拟蒙特卡罗法(quasi-Monte Carlo，QMC)并引入Halton 序列对可靠性灵敏度进行计算，通过对齿轮接触疲劳可靠性及其可靠性敏感性的分析，验证了QMC 方法在计算效率方面的优越性。苏长青等[11]通过对飞机单角拉伸接头进行有限元分析，获得影响可靠性的随机变量参数，并计算得出在多失效模式下的各参数可靠性灵敏度。

由于加工精度、安装误差、温度变化以及振动等各项不确定因素的存在[8]，齿轮弯曲疲劳计算中的各项参数会在符合既定分布的情况下产生随机波动。尽管国内外对齿轮弯曲疲劳可靠性的研究众多，但基于一系列参数于不确定条件下的可靠性灵敏度模型依然很少。本文以渗碳Cr-Ni 齿轮为研究对象，虑及参数不确定条件的影响，为齿轮弯曲疲劳可靠性计算及灵敏度分析方法提供一定的借鉴。

1 齿轮构件及试验

1.1 齿轮构件特性

本文选用渐开线直齿圆柱齿轮作为齿轮弯曲试验构件，其模数为4，齿数为21，齿形角为25°，齿宽为20 mm，表面精度等级为6 级。齿轮的化学成分如表1 所示。

表1 齿轮的化学成分表

对齿轮材料进行表面渗碳、淬火、回火等热处理工艺，以提高齿轮的力学性能，具体流程如图1 所示。

图1 齿轮热处理工艺流程

1.2 疲劳试验

室温条件下，采用LG-300C 高频拉压疲劳试验机进行齿轮弯曲疲劳试验，脉动加载频率约为102 Hz，应力比为0.04。齿轮弯曲疲劳试验机如图2a所示，齿轮疲劳试件的夹紧方法如图2b 所示；由图可知，测试齿轮通过夹具固定在试验机的底部，冲头可以冲击到单齿啮合区域上边界点。为保证试验设备的精度和寿命的安全及稳定性，当载荷或频率下降至5%或者齿根出现可见裂痕时，及时停止试验。考虑到时间及成本条件限制，在706 MPa、744.8 MPa、784 MPa 以及823.2 MPa 这4 种应力水平下，分别记录有效数据各3 组。

图2 应力比为0.04 的齿轮弯曲试验

2 试验结果与分析

2.1 齿轮弯曲疲劳S-N 曲线

在4 种应力水平下，对齿轮开展弯曲疲劳试验，结果如图3 所示。结果表明，疲劳失效循环数在104到108周次之间，且随着弯曲疲劳寿命的增加，渗碳齿轮的弯曲疲劳强度呈连续下降趋势。此外，弯曲疲劳试验数据点在高应力区分散较小，而在低应力区分散较大。基于最大似然拟合方法和Basquin 模型对渗碳齿轮弯曲疲劳数据点进行拟合，得到渗碳齿轮的S-N拟合曲线，结果如图3 实线所示。根据拟合曲线所示，渗碳齿轮在108循环下的弯曲疲劳极限值为666 MPa。

图3 渗碳齿轮S-N 曲线

2.2 齿轮弯曲疲劳P-S-N 曲线

基于SPSS 软件，检验在不同应力水平下的对数疲劳寿命是否服从正态分布，其概率分布如图4所示。

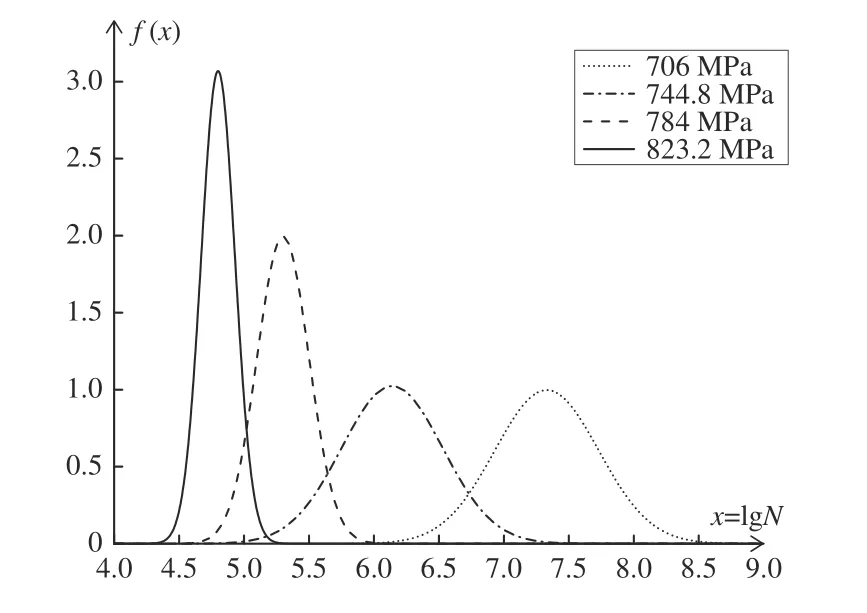
图4 各应力水平下对数疲劳寿命概率密度函数

由图4 可知，各应力水平下对数寿命基本符合正态分布，其均值、标准差等量如表2 所示。

基于表2 中各应力水平下对数疲劳寿命概率密度函数，得到不同失效概率下的疲劳寿命，即P-S-N曲线，其拟合函数为

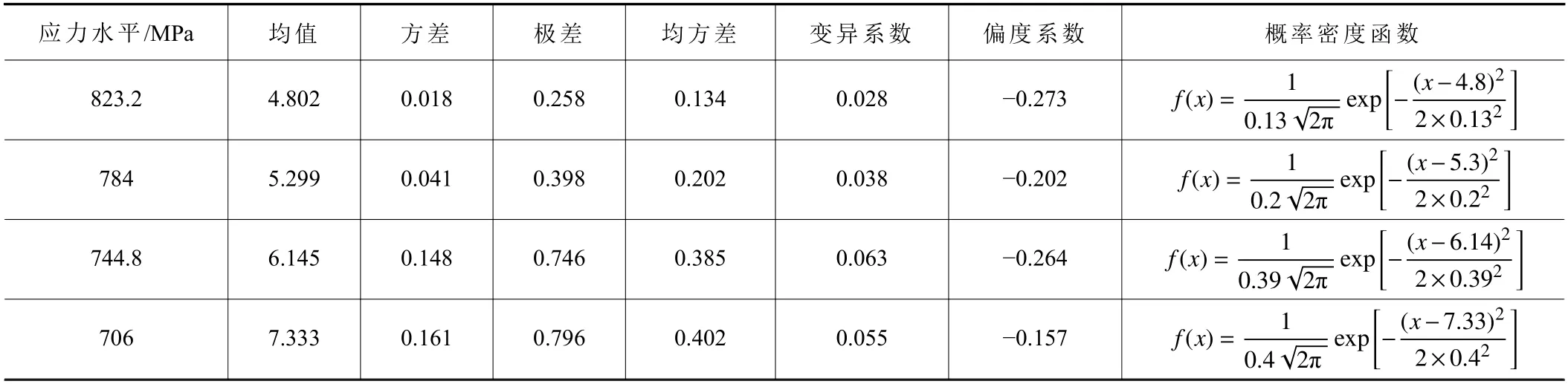
表2 各应力水平下对数疲劳寿命各项参数

结合式（1）及弯曲疲劳试验数据，可得P-SN 曲线如图5 所示；由图5 可知，渗碳齿轮弯曲疲劳试验数据点在所拟合的P-S-N 曲线之内，效果良好。

图5 渗碳齿轮弯曲疲劳P-S-N 曲线

3 弯曲疲劳可靠度模拟

3.1 应力-强度干涉模型

机械产品若要正常使用，在一定的可靠度前提下，危险部位的许用强度S应大于或等于此处的最大应力 σ；否则，认为处于失效状态。一般地，可设零件的强度、应力分布是相互独立的，强度与应力随机变量的概率密度函数可分别设为f(S)、g(σ)，模型如图6 所示。

图6 应力-强度干涉模型

则弯曲疲劳可靠度R为

式（2）所对应的计算式为[12]

3.2 虑及参数不确定性因素的弯曲疲劳可靠度模拟

单齿啮合区上界点所在的圆直径可以通过式（4）计算。

式中：de为啮合上界点所在圆直径；da为齿顶圆直径；db为基圆直径；m为模数；α为啮合角；εα为重合度。重合度εα可通过式（5）计算得出

式中：αa为齿顶压力角；αw为啮合角（分度圆压力角）。齿顶压力角的计算公式为

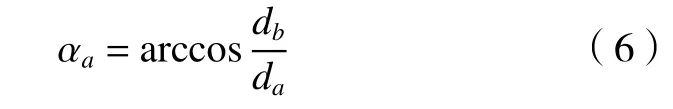
依据齿轮相关参数，结合式（4）～（6），即可得到单齿啮合区上界点所在圆直径。

根据GB/T 14230-93，当脉冲载荷加载在单对齿啮合区上界点时，直齿圆柱齿轮齿根弯曲应力计算公式为[13]

式中：T为对单个轮齿所施加的名义转矩；YF为载荷作用于单齿啮合区上界点时齿形系数；YS为载荷作用于单齿啮合区上界点时的应力修正系数(可视为常数)；b为齿宽；m为齿轮模数；z为齿轮齿数；YST为齿轮的应力修正系数；YδrelT为相对齿根圆角敏感系数；YRrelT为相对齿根表面状况系数；YX为计算弯曲强度的尺寸系数。虑及参数不确定性条件，将参数b、m、YST、YδrelT、YF、YRrelT、YX均视为服从正态分布的随机变量[14-15]。

考虑到式（2）中各个参数的不确定性以及其他计算方法的繁琐性，故根据应力-强度干涉模型，采用蒙特卡罗法进行可靠度求解计算：蒙特卡罗法以样本均值代替总体均值，以足够多的样本可靠度代替总体可靠度计算，计算结果与实际可靠度极其相近，用其进行可靠度计算也是较为广泛的数值模拟方法，且其对于功能函数的维数和分布形式均没有特殊的要求。本文中蒙特卡罗法分析流程如图7 所示。

图7 蒙特卡罗法流程图

结合MATLAB 软件，确定抽样次数为5 000 次，以保证较高的精度。虑及不确定性因素，使应力与强度在符合正态分布的条件下随机产生，由此得到的渗碳齿轮弯曲疲劳极限应力为668 MPa，与图3 中由试验数据拟合得到的疲劳极限值吻合良好。弯曲疲劳极限应力于不同可靠度下的分析结果如表3 所示。

表3 不同可靠度下的齿轮弯曲疲劳极限应力

4 弯曲疲劳可靠性灵敏度分析

4.1 可靠性灵敏度分析理论方法

然而，齿轮弯曲疲劳可靠度对各项参数随机性的响应程度不一；在不同可靠度下，研究齿轮弯曲疲劳对各项参数随机性的响应情况，即可靠性灵敏度分析。可靠性灵敏度的基本定义为失效概率Pf对随机参数xi的数学期望μxi、标准差σxi的偏导

将式(8)转为数学期望的表达式，得

采用蒙特卡罗法计算齿轮弯曲疲劳可靠性灵敏度，总期望由样本期望代替，则均值灵敏度为

同理，总标准差由样本标准差代替，则标准差灵敏度为

式中：L为蒙特卡罗法样本数，E[ ]为样本的数学期望，fx(x)为随机参数的联合概率密度函数IF(x)=为齿根失效区域F的表达函数。

由于影响齿轮弯曲疲劳可靠性灵敏度的各项随机参数具有不同的量纲，只有消除量纲对失效概率的影响，才能使各项参数对失效概率的影响程度更好地表达。因此，无量纲的均值灵敏度由式（12）可得。

由于各项随机参数均服从正态分布，则

式中：μi为对随即参数x=(x1,x2,···,xn)T中第i个分量xi引入的标准正态变量。

因此，去除量纲影响后的均值失效灵敏度为

式中：μji为第j个样本xj=(x1,x2,···,xn)的第i个分量xji所对应的标准正态化样本。

由式（15）、（16）可得到不同可靠度下去量纲参数的均值灵敏度和方差灵敏度。

4.2 基于参数不确定性的弯曲疲劳可靠性灵敏度分析

根据表3 中齿轮弯曲疲劳可靠度分别为99%、90%、50%、10%、1%时所对应的各个齿轮弯曲应力，分析各个参数对齿轮弯曲疲劳可靠性的影响状况。基于式(15)、(16)，并结合蒙特卡罗法，可以得到去除量纲后各项随机参数于不同可靠度下的均值灵敏度和方差灵敏度，如图8 所示。

图8 不同可靠度下齿轮弯曲疲劳可靠性灵敏度

结合图8 可知，本试验中影响齿轮弯曲疲劳可靠性的7 个参数的均值灵敏度在各个可靠度下的变化均有正有负，且绝对值较小，表明它们的均值变化对可靠性的影响存在正相关和负相关，且影响较为平缓；而包括b、YST、YδrelT、YRrelT、YX及m在内的共6 个参数的方差灵敏度在各可靠度下均为正值，且绝对值较大，表明随着这些随机参数的方差增大，齿轮弯曲疲劳可靠度会剧烈地增大，其影响是积极的；而齿形系数YF的方差灵敏度在各可靠度下均为负值，且绝对值极小，表明随着此随机参数的方差增大，齿轮弯曲疲劳可靠度就会极缓地减小，其影响是消极的。