表面等离子波导系统中基于远场耦合的可控单向无反射

何志伟， 金星日

(延边大学 理学院， 吉林 延吉 133002)

0 引言

1998年， Bender等[1]研究表明满足宇称-时间(parity-time， PT)对称的非厄米哈密顿也可以具有实数本征值.近年来随着研究的深入，学者们在非厄米光学系统中又发现了许多奇特的现象，如非互易光传输[2-3]、电磁诱导透明[4-5]、相干完美吸收[6-7]和单向无反射[8-17]等.2011年，Lin等[8]在非厄米光学系统中首次发现了单向无反射现象，即在由均匀电介质材料包裹的光学增益和损耗材料组成的PT对称结构中发现，当电磁波入射到该结构时，电磁波在异常点处出现了单向无反射现象.2013年， Feng等[10]利用由二氧化硅包裹的硅和锗/铬双层结构镶嵌的硅波导所组成的PT对称结构实现了单向无反射现象.基于上述研究，近年来一些学者利用表面等离子波导系统研究了单向无反射现象.例如： 2015年， Huang等[11]在非PT对称表面等离子波导-腔耦合系统中基于数值模拟研究了单频带单向无反射现象； 2016年， Huang等[12]利用具有非平衡增益损耗的表面等离子波导-腔耦合系统实现了宽带单向无反射； 2017年， Zhang等基于近场耦合[13]和远场耦合[14]，利用两个柱形共振器边耦合于金属-绝缘体-金属(MIM)表面等离子波导系统实现了单频带单向无反射现象.随后， Zhang等[15]又利用电磁诱导类透明效应的3个共振器耦合MIM表面等离子波导系统实现了双频带单向无反射； 2019年， Zhao等[16]利用两个纳米孔共振器端耦合MIM表面等离子波导系统实现了双频带单向无反射； 2020年， Yu等[17]将两个矩形电光材料共振器近场耦合于表面等离子波导系统，并通过施加外部电压实现了可控单频带单向无反射.基于上述研究，本文设计了一个由两个电光材料共振器边耦合于表面等离子波导的系统，并基于远场耦合研究了该系统的单向无反射现象.

1 模型与计算

本文基于法布里-珀罗共振原理设计了一个由两个电光材料共振器边耦合于表面等离子波导的系统，如图1所示.图中：共振器A和B的长度分别为l=280 nm和h=138 nm， 两个共振器的间距d为218 nm，共振器A与表面等离子波导的间隙n为13 nm， 共振器A、B及表面等离子波导的宽度w均为50 nm.图中灰色区域为金属银，白色区域(矩形共振器和表面等离子波导部分)是由电光材料(4-(4-二甲基氨基苯乙烯基)甲基吡啶对甲苯磺酸盐(DAST))填充的.外部电压施加在结构上下的两个银板上，用以改变上下银板间的电势差，进而改变共振器B和表面等离子波导中的电光材料的折射率.由于共振器A处于恒定电势下，因此其折射率保持不变.电光材料折射率nDAST随电压的变化关系[18]为：

(1)

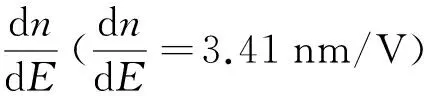
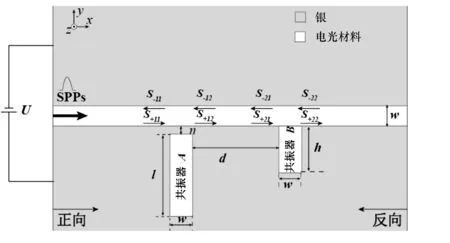
图1 共振器与表面等离子波导耦合系统的结构

下面利用传输矩阵来进一步分析系统的散射特性.基于非厄米系统(图1)的传输矩阵M为：

(2)

(3)

(4)

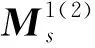
(5)

其中rf(rb)和tf(tb)分别为表面等离子波正向(反向)的反射系数和透射系数.

2 结果与讨论

利用CST数值模拟和传输矩阵分析所得的结果绘制不同电压下反射率随频率的变化关系图，如图2所示.图2中，实线和点线分别表示数值模拟获得的正向和反向反射光谱，三角线和圆线分别表示分析计算获得的正向和反向反射光谱.由图2可见，除高反射区域存在差异外(由不可避免的误差导致)，数值模拟和传输矩阵分析所得结果基本保持一致性.在图2(a)中，分析计算所采用的参数分别为ωa1=151.9 THz,ωa2=158.9 THz,Γa1=2.39 THz,Γa2=2.12 THz，γa1=8.5 THz，γa2=11.9 THz，φa=0.909π.在图2(b)中，分析计算所采用的参数分别为ωb1=151.9 THz，ωb2=147.9 THz， Γb1=2.11 THz，Γb2=2.86 THz，γb1=13.12 THz，γb2=11.69 THz，φb=0.845π.由图2(a)可以看出，当电压为2.75 V时，157.36 THz处的正向反射率接近0， 反向反射率接近0.71， 且此时出现了单向无反射现象.由图2(b)可以看出，当电压为9.47 V时，156.48 THz处的反向反射率接近于0， 正向反射率接近0.58，且此时出现了单向无反射.由此可知，通过调节外部电压可以控制单向无反射现象的出现.

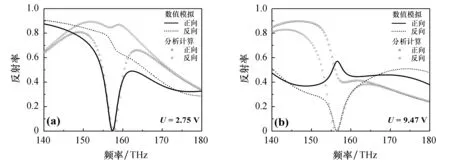
图2 不同电压下反射率随频率的变化关系

为了进一步分析单向无反射出现的机制，利用数值模拟的方法绘制系统在频率为157.36 THz和156.48 THz处的z-分量磁场分布，如图3所示.由图3可以看出，在电磁波为正向和反向入射时，两个共振器的z-分量磁场分布都出现了强激发和弱激发效应.基于法布里-珀罗共振原理可知：在频率157.36 THz处正向入射时(外部电压U=2.75 V)两个共振器诱导的磁场方向是相同的，这表明两个共振器间的相位差接近2π； 而当反向入射时两个共振器的诱导磁场方向是相反的，这表明两个共振器的相位差接近π.由此可知图3(a)和图3(b)分别对应于低反射和高反射，该结果与图2(a)所示的结果一致.在频率156.48 THz处正向和反向入射时(外部电压U= 9.47 V)，两个共振器的诱导磁场方向分别是相反和相同的，这表明两个共振器间的相位差分别接近π和2π， 因此导致了高反射(图3(c))和低反射(图3(d))的出现，该结果与图2(b)所示的结果一致.综上可知，当调整电压至2.75 V和9.47 V时，在频率157.36 THz和156.48 THz处可实现可控的单向无反射.

图3 不同电压下的z-分量磁场分布

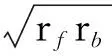
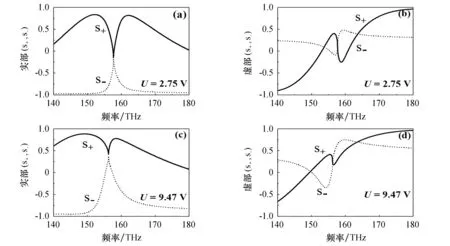
图4 不同电压下的本征值的实部和虚部曲线

图5为正向和反向的反射光谱随外部电压的变化关系.由图5(a)可知，正向低反射峰(黑色区域)出现在0～5 V的电压范围内，且在电压由0 V增加到5 V时未发生明显变化.由图5(b)可知，当电压从～5 V增大到～16 V时，反向低反射峰发生轻微红移.这是由于共振器B的折射率会随电压的增加而发生改变，进而导致共振频率发生红移.此外，正向的低反射区域(黑色)对应于反向的高反射区域(白色)，反之亦然.以上结果表明，可以在较宽的电压范围内实现单向无反射.

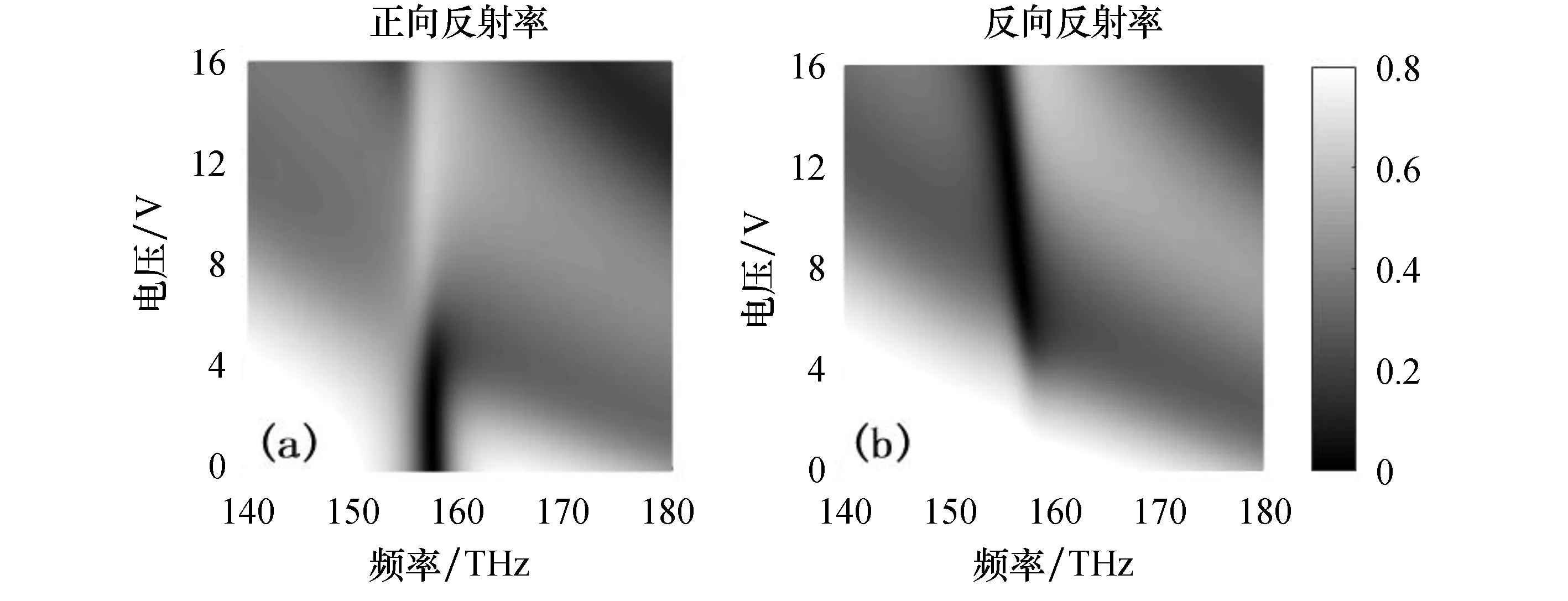
图5 反射光谱随外部电压和频率的变化关系

图6为当外部电压U为2.75 V和9.47 V时，正向和反向反射随两个共振器间距d的变化关系.由图6(a)可知，当距离从～100 nm增大到～250 nm时正向低反射峰(黑色区域)没有发生明显变化，这表明反射光谱对两个共振器间距的变化并不敏感.由图6(d)可知，随着间距d的增加，反向低反射峰(黑色区域)出现轻微的红移现象.对比图6(a)和图6(b)以及图6(c)和图6(d)可以发现，在频率～157 THz附近，图6(a)和图6(d)中的黑色低反射区域分别对应于图6(b)和图6(c)中的白色高反射区域.上述结果表明，单向无反射可以出现在较宽的间距范围内.

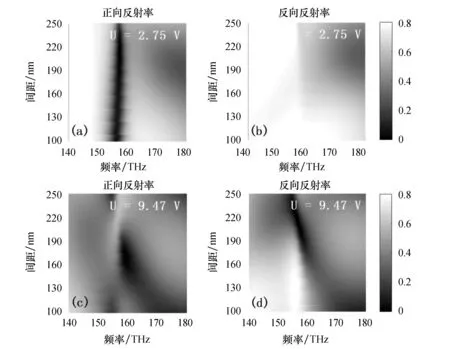
图6 不同电压下反射光谱随共振器间距d的变化

图7为反射光谱随共振器A与表面等离子波导的间隙n的变化关系.由图7可以看出：图7(a)和图7(d)中的低反射峰(黑色区域)出现在～5 nm到～25 nm的范围内，且随着间隙的增大发生明显的蓝移；图7(a)和图7(d)中的黑色低反射区域分别对应于图7(b)和图7(c)中的白色高反射区域，反之亦然.由此表明，单向无反射可以出现在较宽的间隙范围内.

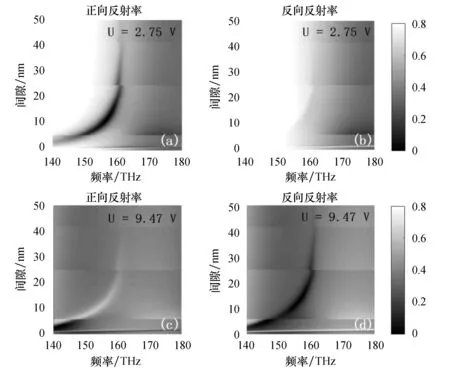
图7 不同电压下反射光谱随间隙n的变化

图8为反射光谱随共振器B的长度h的变化关系.由图8(a)可以看出，正向低反射峰(黑色区域)并未随着长度h的增加而发生明显变化；由图8(b)可以看出，当长度h超过～115 nm时，反向高反射峰(白色区域)出现轻微的红移现象，这是由于增大长度而导致共振频率减小引起的.图8(a)(电压为2.75 V)中的低反射峰出现在较宽的长度范围内(～80 nm到～150 nm)，图8(d)(电压为9.47 V)中的低反射峰出现在较窄的长度范围内(～115 nm到～150 nm).图8(a)和图8(d)中的黑色低反射区域对应于图8(b)和图8(c)中的白色高反射区域，反之亦然.以上结果表明，共振器B在较宽的长度范围内可以实现单向无反射.

图8 不同电压下反射光谱随长度h的变化关系

3 结论

通过对本文设计的一个由两个共振器边耦合于表面等离子波导组成的系统进行研究表明，当外部电压U=2.75 V(9.47 V)时，正向反射率接近0(0.58)，反向反射率接近0.71(0)，由此可知通过调节外部电压可以实现可控的单向无反射.此外研究还显示，单向无反射现象可以在较宽的电压范围、共振器间距范围、共振器A与表面等离子波导的间隙范围及共振器B的长度范围内实现.本文研究结果可为研发光二极管、电光开关、滤波器、传感器等元件提供理论参考.