中红外波段超广角抗反射微纳结构的研究
2022-08-25张艺馨张亢林鹤吴锦双沈思彤付跃刚
张艺馨,张亢,林鹤,吴锦双,沈思彤,付跃刚
(1.长春理工大学 光电工程学院,长春 130022;2.中国空间技术研究院西安分院,西安 710000;3.中国科学院光电技术研究所微细加工光学技术国家重点实验室,成都 601209;4.长春理工大学 光电测控与光信息传输技术教育部重点实验室,长春 130022)
亚波长结构作为具有渐变折射率的人工材料,通过相位累计效应实现渐变折射率[1]。以其尺寸小、抗串扰能力强[2-4]、设计自由度大等优势,广泛应用于红外导引头[5]、航天探测器、光学窗口[6-7]等光学器件中,用以减小反射引起的光能损失[8-10]。微纳结构表面的抗反射性能对入射角度响应较大,随着角度增大,抗反射性能的降低对太阳能电池等光学器件的工作效率有较大影响。但现阶段对于大角度抗反射的超构表面研究多在70°以内,且多集中于可见光以及近红外波长范围内。Bruynooghes等人[11]在350~1 150 nm 波段范围内对表面在 20°、40°和 60°入射时的抗反射性能进行了比较,当入射角为60°时,反射率在可见光波段低于10%,在近红外波段反射率较高。李资政等人[12]通过对硅表面进行湿法刻蚀得到了亚波长结构表面,其工作波段在 400~1 400 nm,入射角度为 0°~45°,整个工作谱段反射率低于5%,最低反射率在1%左右。韩国 Leem J W 等人[13]在 350~900 nm 波段范围内,研究了3°~80°入射角时亚波长结构的抗反射特性,结果表明反射率平均可达6%。
本文采用时域有限差分法(FDTD)对不同结构进行仿真,对比不同形貌结构角度-反射率曲线,并在超广角范围对结构的周期、底端直径、结构高度和顶端直径进行参数优化,分析各参数对透过率的影响。这一表面结构对实现中红外波段光学器件抗反射性能的提升,为亚波长结构在红外波段的大角度抗反射设计提供了新的思路。
1 理论模型与仿真分析
1.1 理论模型的建立
为确定仿真结构,分别对圆台、圆锥和棱台、棱锥结构在相同的周期、底端直径、结构高度情况下的反射率随入射角变化的仿真结果进行了对比。由图1所示,入射角在15°~70°范围内各结构的反射率均出现不同程度的升高,但当入射角大于70°时,四棱台结构对角度响应表现更加稳定,故在超广角范围内设计减反射结构时,选择四棱台结构作为优化对象。

图1 不同结构入射角与反射率关系曲线
以底面中心点为原点建立直角坐标系并建立仿真模型,如图2(a)所示,单元几何参数如图2(b)所示。其中入射角为θ(15°~80°),D和d分别为表面四棱台单元结构的上底边和下底边长;H为结构高度;γ为侧面与下底面夹角。在结构表面任取一点A(x,y,z),令q为点A为所在棱台侧面的垂直坐标面上的投影长度,则形貌表达式如下:


图2 亚波长抗反射结构理论模型
在计算反射率时,使用工作波段在3~5µm的平面波光源,入射角度在15°~80°,为了弥补斜入射时相位对反射的影响,在x和y方向上选择Bloch作为边界条件,而z方向上选择完美吸收边界(PML)作为边界条件。本文通过对结构高度、周期、底端直径、占空比等多个参数进行对比,选取最优设计参数,并对其进行多次仿真计算,取平均值作为最终计算结果,以确保结果的可靠性。
1.2 仿真结果对比与分析
对超广角亚波长减反射结构的反射率进行定量计算,公式为[14]:
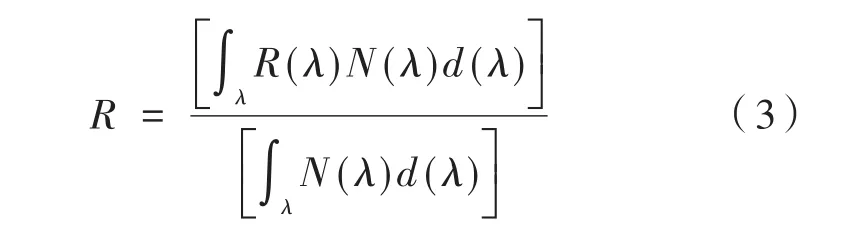
式中,λ为入射波长;R(λ)为光谱反射率;N(λ)为单位波长单位面积太阳能辐射的光子数;R为反射率。
1.2.1 15°入射时结构参数随波长变化对反射率的影响
为确定结构参数,根据控制变量的方法,首先对入射角为15°时进行讨论,研究了入射波长为3~5µm时底端直径D、顶端直径d、结构高度H以及周期Λ对反射率的影响。
当周期Λ为1.6~2.4µm时,其他参数固定(D=1.0µm,d=0.1µm,H=3.4µm)。如图3(a)所示,在工作波段内,选取了Λ为1.6µm、1.8µm、2.0µm、2.2µm、2.4µm分别进行了反射率仿真。结果显示随周期增加反射率整体逐渐升高,同时由于周期不断增大,相应的底面占空比降低,反射率升高速度增快,反射率最小极值点增大,因此可得结论:在小角度斜入射时底面占空比越高则其反射率越低。
当顶端直径d的变化范围为0.1~0.9µm时,其他参数固定(D=1.0µm,H=3.4µm,Λ=2.0µm),由图3(b)可以得到随顶端直径的增大,结构的平均反射率升高并在d>0.7µm时反射率波动较大。由于顶端直径的增大,使得结构逐渐接近四棱柱结构,可证明在中长波红外波段内四棱台结构的抗反射特性明显优于四棱柱结构。
在图3(c)中分析了底端直径D变化时对工作波段内结构反射率的影响。选择了1.0µm、1.4µm、1.6µm、1.8µm、2.0µm的底端直径进行分析,其他结构参数固定(d=0.1µm,H=3.4µm,Λ=2.0µm)。从图中可以看出随底端直径的增加,结构反射率逐渐降低。当结构的底端直径增加到近似周期大小时,平均反射率低于5%,在4.4~5µm时反射率低于1.5%。占空比与底端直径成正比,折射率梯度分布均匀,光能反射率降低。
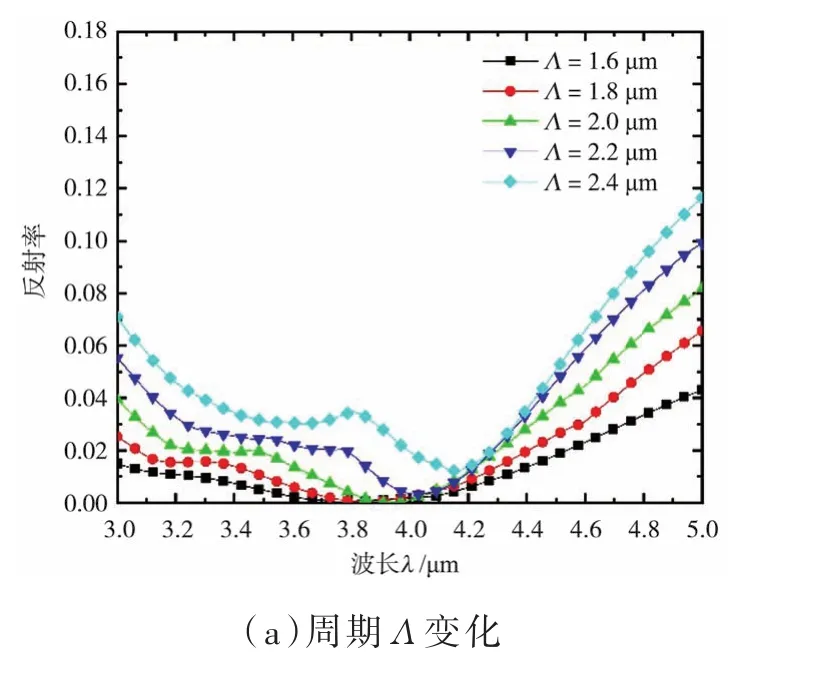

图3 入射角为15°时3~5µm反射率与亚波长结构参数的关系曲线
其他结构参数固定后(d=0.1µm,D=1.0µm,Λ=2.0µm),对H在2.6~3.4µm范围内进行分析。H对反射率的影响分析如图3(d)曲线所示,随H增高反射率逐渐降低。根据等效介质理论,H的增加使纵向结构等效膜层数增加,梯度折射率纵向变化间隔减小,介质层的菲涅尔反射减小,反射率降低。
1.2.2 入射光波为4µm时结构参数随角度变化对反射率的影响
结构参数初步确定后,为了研究超广角入射时的结构反射率以及此时各几何参数对反射率的影响,并对结构参数进行优化与仿真分析。使用FDTD-Solutions软件在入射波长为4µm时进行入射角15°~80°的扫描分析,改变结构的周期Λ、底端直径D、结构高度H和顶端直径d,并对相应的反射率进行比对。
当周期Λ为1.6~2.4µm时,其他参数固定(D=1.0 µm,d=0.1 µm,H=3.4 µm),如图4(a)所示,随着周期的增大平均反射率增高。当θ>70°时,反射率升高,速度迅速增快,在80°时透过率达到最高,距最低点升高20%以上。同时当占空比大于1/2时,反射率15°~70°之间反射率波动较大,即占空比小于1/2时,亚波长结构的光谱传输共振明显增强,有效减少了表面光能的反射损耗。
与周期对结构抗反射性能调控的机制相同,在周期等其他参量不变的情况下,底端直径通过改变底面占空比来调制表面反射率。D的取值范围范围在1.0~1.6µm,其他结构参数固定(d=0.1 µm,H=3.4 µm,Λ=2.0 µm)时,如图 4(b)的反射率曲线所示,在1.0µm≤D≤1.6µm时平均反射率与D成正比;当1.6µm ≤D≤2.0µm时则与D成反比,但平均反射率在D=1.0µm时取到最低,验证了前文周期的仿真结果,即占空比为1/2时反射率最低。
而在图4(c)的反射率曲线中可以看出,当结构高度H的变化在2.6~3.4µm范围内,且d=0.1µm,D=1.0µm,Λ=2.0µm时,随入射角度θ增大,整体反射率趋势呈先缓慢降低,在60°取得最低点,后在入射角大于70°时迅速升高。在15°~60°范围内反射率对结构高度的改变响应很小,当入射角θ大于60°时,入射角度逐渐超过布鲁斯特角(tanθB),此时H对反射率影响增大。从曲线整体来看,随结构高度的增加,平均反射率降低,且角度越大,高度对反射率的影响越明显。即与小角度斜入射时对比来看,大角度入射时反射率对于介质折射率变化平滑程度的响应更加明显。

图4 超广角反射率与亚波长结构参数随角度的变化关系曲线
图 4(d)中,顶端直径d在 0.1~0.9 µm,其他结构参数(D=1.0µm,H=3.4µm,Λ=2.0µm)不变时,d的增大使得反射率明显升高,且整体反射率的升高幅度随入射角度θ增加而增大。
从整体来看,当结构参数固定,斜入射角度15°~30°之间时,角度对于反射率的影响较小,而随着入射角度的增大,反射率明显呈上升趋势,在80°的反射率最高。而在比较周期、底端直径、结构高度、顶端直径四个结构参数后,对于大角度入射时底端直径和结构高度的容差范围较大,而占空比和底角大小对于反射率影响较大,最优结果如图5所示。

图5 中红外四棱台抗反射结构透过率随角度变化最优结果
1.2.3 比较同底角与占空比时结构形貌对反射率的影响
根据上文中的仿真数据整理发现,当结构高度与底段直径之比约为3∶1时得到结构的超广角抗反射特性最优,此时的底角γ约为83°,此时的入射光线相较于棱台斜面近似于正入射,使得大角度入射时结构可以很好调控反射率。为进一步论证超广角斜入射时占空比与底角对反射率的影响,现固定占空比即仿真周期(Λ=2.0µm)与底端直径(D=1.0 µm)以及底角(γ=82.5°),对不同结构形貌的角度-反射率曲线进行对比,如图6所示。

图6 不同形貌结构的角度-反射率曲线对比结果
为保证四种形貌结构的底角γ不变,由公式(1)可知,锥形结构的高度为3.8µm,而台结构的高度为3.4µm。但如图5结果所示,锥结构与台结构的整体透过率一致,而圆形截面结构与矩形截面结构在大角度斜入射时,平均透过率差异不大。由此可以看出,在保证占空比与底角的情况下,对于入射光波的电磁场矢量垂直于结构斜面的分量逐渐增大并被结构捕获,在内部多次反射后传播至基底,从而降低了表面反射率。
2 结论
亚波长抗反射结构被广泛应用于光学窗口。能量探测器等光学器件中,为解决由于大角度入射时光能损失的问题,本研究通过对周期、底端直径、结构高度、顶端直径进行调整,应用时域有限差分法对3~5µm的工作波段内,入射角为15°~80°的Si四棱台结构进行结构参数的优化,最终得到了在15°~80°斜入射时工作波段的平均反射率达到5%,最低反射率可达到0.01%亚波长结构表面。并分析出,对于大角度入射时结构底角与占空比为影响表面反射率的主要因素,同时也为中红外波段光学器件在大角度入射时的应用提供了新的设计思路和理论支持。
