高等数学中不定积分类问题的解决方法

杨 金 梅

(青海民族大学预科教育学院，西宁 810007)

不定积分是微分或求导的逆运算，也是应用莱布尼茨公式的知识。不定积分可以将积分学知识和微分学知识联系起来，帮助学生系统学习高等数学。不定积分的求解过程就是利用函数求导结果解出原函数，即找到被积函数的过程。因此，积分学课程一般安排在微分学课程之后。解决不定积分问题比求解微分和求导难度更大，因为只要函数可导，无论形式多么复杂，学生只需按照求导公式、导数运算法则和导数定义即可解决相关问题[1]，而解决不定积分问题时，利用公式和运算法则只能解决少数简单题目，其他问题则需要学生根据对应的解题方法，具有很大的灵活性和技巧性。

一、不定积分概述

不定积分最初是根据几何重心、立体图形体系、平面图形面积的求解需求产生的。阿基米德(Archimedes)在《方法论》中首次提出上述计算原理，将所求面积看作无穷多条线段积分构成，并利用该原理求解出部分曲边多边形的面积。随着人们对该方法研究和理解的不断深入，牛顿(Newton)和莱布尼茨(Leibniz)在17世纪总结前人研究方法，并将积分法进行推广，被大众熟知[2]。

(一)原函数与不定积分

解决不定积分相关问题要有一定的灵活性和技巧性，学生首先需要理解和掌握原函数与不定积分的概念以及二者间存在的联系，才能进一步学习不定积分计算方法，掌握解题技巧，为以后学习奠定基础。

其一，原函数定义。倘若区间I上，可导函数F(x)的导函数是f(x)，那么任意x∈I，有F′(x)=f(x)或dF(x)=f(x)dx，则函数F(x)为f(x)在区间I上的原函数[3]。

值得注意的是，上述公式成立的条件是任意x属于区间I，所以原函数存在的区间为I。上述公式成立的区间与原函数所在的区间相同。原函数的定义是学生最易忽略的地方，也是后期解决不定积分相关问题时非常容易出现漏接或错解的地方。此外，常数导数为0，如果F(x)是区间I上f(x)的原函数，则[F(x)+C]′=f(x)。因此，f(x)在区间I上有无穷个对应的原函数。

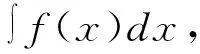
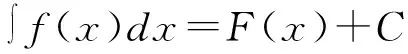
从上述定义可知，原函数与不定积分的关系，即微分运算与积分运算存在互逆的关系。

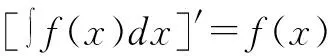
(1)

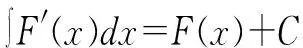
上述公式中，公式(1)表明先进性积分运算，然后进行微分运算，两种运算可相互抵消；公式(2)表明先进性微分运算，接着进行积分运算，最终还会留下任意常数C。所以，学生在实际解决不定积分相关问题时，可以对积分运算结果进行求导，判断求导结果与被积函数是否一致，以验证积分运算的正确性。此外，学生求解不定积分相关题目时应该注意，不定积分求解最终必须加上积分常数C，证明原函数F(x)存在无穷多个，表明求解得出了全体原函数。

(二)学习不定积分解决方法的重要性

在解决不定积分相关问题时，需要运用数学思想和数学逻辑思维能力。因此，学习不定积分解决方法，可以发散学生的思维，培养和提升学生的数学综合素养，为学生以后学习其他知识奠定基础。

高等数学同一题目存在多种不同解法。如果学生可以在多种解题方法中找到最佳解题方法，不仅可以提高解决问题的速率，而且可以提升解决问题的准确性，快速高效地得到结果。不定积分教学内容是一题多解的典型案例，教师引导学生学习时要提高重视程度[5]。学生不定积分相关题目时，要注意题目的特征，找到与之相适应的解题方法，然后筛选出解题过程最简单、正确率最高的解题方法，快速高效地完成解题任务。学生筛选最优解题方法的过程就是分散思维、培养数学思维的过程。教师可以根据学生应用技巧解决问题的灵活性和正确率等来了解学生学习不定积分内容存在的薄弱环节，判断学生的数学素养，在教学中采取针对性训练措施，因材施教，逐步提升学生的高等数学学习成绩，提高教学质量。

二、求解不定积分相关问题的方法

高等数学不定积分教学中，解题方法包括积分公式法、凑微分法、第二换元法、分部积分法等方法。虽然解题方法有多种，但学生初步接触不定积分时常出现使用混乱的现象，遇到不定积分题目时不知道该如何选择解题方法。正确了解和掌握不定积分解题方法的种类，并能将每种解题方法应用于实际解题过程中，是教师讲授不定积分教学内容的重难点。

(一)积分公式法

积分公式是求解不定积分相关问题的基础，无论哪种形式的不定积分题目，不管采取哪种解题方法，最终都必须使用积分公式才能得到答案。所以，学生学习不定积分内容时，首先应当牢固掌握基本积分公式。基本积分公式由不定积分定义和基本求导公式得出，学生只需要结合不定积分定义和基本求导公式，就能够掌握积分公式。积分公式法通常被称为“直接积分法”，即只需要根据不定积分的运算法则和性质，结合积分公式便可得到答案。以下15个基本积分公式可直接由基本求导公式得到，如表1所示。

表1 基本积分表

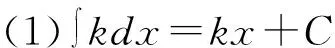
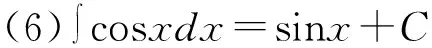
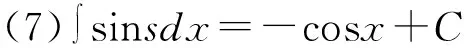
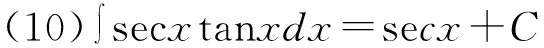
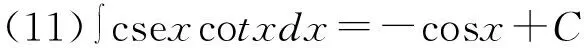
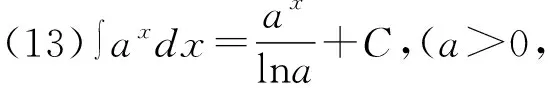
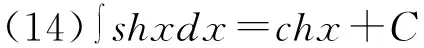
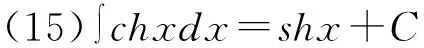
除上述直接推导出的积分公式外，部分不定积分题目需要利用三角恒等式、代数等内容将被积函数转变为代数和形式，然后结合积分性质和积分公式求解[6]。

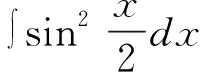
(二)凑微分法(第一类换元法)

凑微分法也被称为“第一类换元法”，是后述几种不定积分解题方法的基础，主要将复合函数相关的求导法则逆向应用于求解不定积分相关问题。因为该方法并不是真正的换元，所以凑微分这一名称直接表明了该解题方法的本质特征。凑微分法以一元函数一阶微分不变形原理为基础，利用逆向思维将目标题目进行转化，然后使用基本积分公式进行求解[7]。使用凑微分法解题的前提是熟练掌握和使用求导公式，所以学生必须牢固掌握初等函数和常见求导公式。凑微分法的解题难点在于学生需要凭借直觉思维能力，判断将被积函数哪部分进行凑微分，才能顺利解题。教师在教学过程中需要引导学生及时归纳和总结常用微分公式，并加以练习，培养学生的直觉思维能力。在实际解题中，学生可以凭借对基础知识、经验和联想的综合运用，迅速找到正确解题思路。凑微分公式如下：

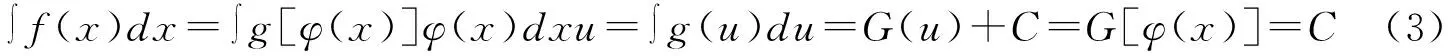
从上述凑微分公式可知，“凑”的主要目的是使,被积函数g[φ(x)]的中间变量φ(x)与积分变量dφ(x)相同[8]。

高数不定积分常见的凑微分公式：

(7)sinxdx=-dcosx

(8)cosxdx=dsinx

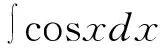
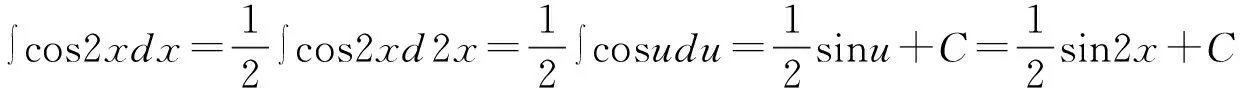
上述解题过程首先进行凑微分，然后将2x=u带入，并用基本积分公式进行积分，然后将u=2x带回，即可得到正确答案。熟练后可直接使用常用的凑微分公式得到答案。

(三)第二类换元法

第二类换元法即变量代换法，利用直接换元，可将形式较为复杂的不定积分转变为形式更为简单的积分[9]。第二类换元法可分为三角代换、倒代换和无理代换，比第一类换元法更容易掌握。虽然第二类换元法原理较为简单，但在实际解题过程中需要掌握一定的规律和解题技巧，学生必须及时转换思维，才能找到正确的解题方法。第二类换元法公式如下：

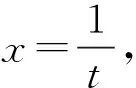
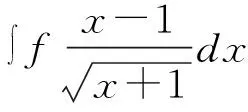
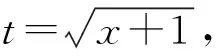
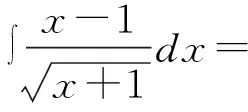
(四)分部积分法

分部积分法也被称为“循环法”，是求解不定积分的另一种方法。利用分部积分法解决不定积分相关问题的关键在于将求解难度较大的被积函数进行分离，对已进行求解的被积函数进行凑微分，然后利用分部积分公式进行求解[10]。分部积分法主要运用于被积函数为两种类型不同的函数相乘不定积分题目中，分部积分的公式为：

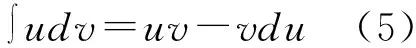
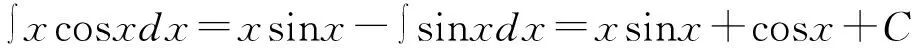
不定积分相关题目形式繁多，相应的求解方法也多。除上述四种基本求解方法外，还有部分消元法、填项法等，但万变不离其宗，解答不定积分相关问题的关键在于将目标题目中的被积函数转换为基本积分公式中存在的函数形式。此外，一题多解是不定积分相关题目的特点，教师在教学过程中可以有意识地引导学生对几种基本解题方法进行比较，帮助学生掌握解题技巧，培养学生的数学思维。

三、解决不定积分相关问题常见错误

不定积分相关题目的计算是不定积分教学内容的重点，学生必须在日常学习和练习中牢固掌握解题方法，才能为后期学习定积分、二重积分、曲线积分等知识奠定基础。由于不定积分学习和理解难度较大，部分学生对解题方法的理解流于表面，没有认识到解题方法的本质，难以做到举一反三，解决不定积分问题时常出现以下错误。

(一)自变量与积分变量混淆

一般而言，基本积分公式中的自变量和积分变量都是x，但多数不定积分题目中积分变量和被积函数并不相同，但学生在解题过程中常常会忽视这一点，混淆自变量和积分变量，导致解题错误。

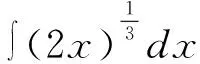
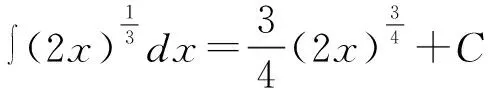
由于基本积分公式中被积函数为幂函数，且自变量与积分变量是一致的，如果上述两个条件有一个不能满足，则上述基本积分公式是不成立的。显然求解的不定积分题目并不满足第二个条件，其自变量为2x，而积分变量为x，所以，利用积分公式法得到的答案是错误的。解决上述例题有两种方法，一种是直接利用不定积分的性质解题，另一种为凑微分法。

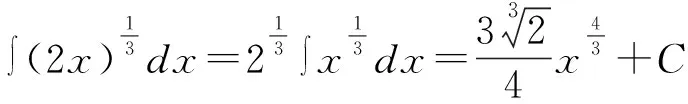
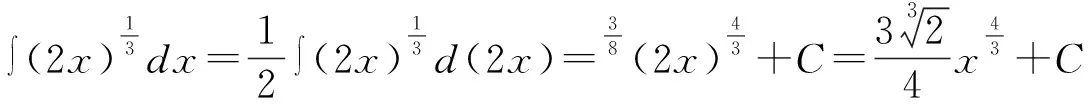
(二)不定积分性质掌握不牢固

学生在学习不定积分相关知识初期，基本知识理解和掌握不够牢固，对不定积分的性质理解存在偏差，存在根据题目自主创造积分公式的错误。不定积分的性质之一为不定积分中被积函数为有限个函数的差或和等于有限个不定积分的差或和，换言之，不定积分中被积函数为任意常数和某一函数乘积，则可将常数直接移到积分号前。

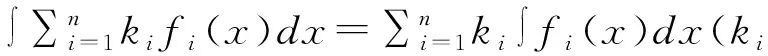
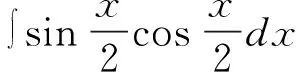
错误解法：学生会根据不定积分性质直接将被积函数分成两部分积分然后相乘。

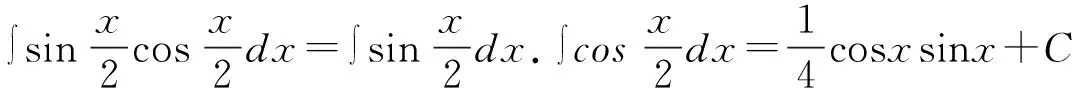
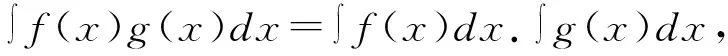
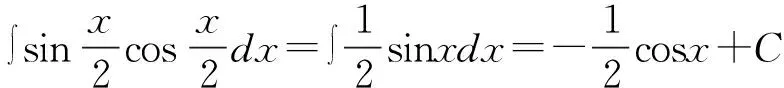
除上述错误外，学生在解答不定积分问题时还会出现利用第二类换元法解题时，忘记将变量带回；积分结果中忘记加上任意常数C；解题过程中，特别是解答分段函数不定积分问题时，忽略被积函数的定义域和连续性等问题。究其原因，都是学生对不定积分定义、性质及基本积分公式的理解和掌握不够牢固，对解题方法和技巧的运用不够熟练所致。学生需要勤加练习、总结，形成解题思维，才能够在实际应用中迅速找到正确解题思路，得到正确答案。