基于复调制细化和Adaline网络的谐波检测方法

窦嘉铭，马鸿雁,2,3

(1. 北京建筑大学电气与信息工程学院，北京 100044; 2. 分布式储能安全大数据研究所，北京 100044;3. 建筑大数据智能处理方法研究北京市重点实验室，北京 100044)

0 引言

随着现代社会电力电子技术的迅猛发展，电力系统谐波问题日益严重，对电力系统的安全稳定运行产生巨大影响，治理谐波刻不容缓[1]。只有明确掌握电网中谐波的实际情况，才能进一步对谐波进行抑制或者消除。因此，谐波检测作为谐波治理的首要环节，其重要性不言而喻。

历史上曾经出现过的谐波检测方法包括傅里叶变换、小波变换及小波神经网络、瞬时无功功率、现代谱估计、神经网络等等[2]。傅里叶变换是根据傅里叶分析的数学理论来进行计算的方法。但是由于电力系统的工频往往不是恒定值，而是在工频左右的微小范围内变化，导致傅里叶变换后的频谱存在栅栏效应和泄露现象，使得计算出的电流信号频率、相位和幅值存在较大误差，且时效性较差[3-4]。以ip～iq法为代表的瞬时无功功率方法计算量大、矢量变换复杂，存在检测准确度不高，对电网频率敏感等问题[5]。

基于人工神经网络的谐波检测方法是近20年来出现的新方法，受到关注较多。有两种不同的技术路线[6]：第一种是多层前向神经网络（MLFNN），包括BP神经网络、RBF神经网络等等[7-10]，该方法首先使用历史数据对网络进行训练，然后将获得的信号输入已经训练好的网络中，再从输出端得到谐波的各项参数。但该方法的存在易陷入局部最优、计算量大、难以解释物理意义[11]、对变化的谐波难以检测等问题，无法满足实际应用的要求[4]；第二类是包括Adaline网络在内的自适应神经网络方法。该方法无需事先对神经网络权值进行样本训练，而是先通过学习使信号的估计值与实际采样值之间的误差达到最小，然后再根据网络参数求得谐波的频率、幅值和相位[9]。但该方法最大的缺点在于需要已知系统的精确基波频率，才能进行高准确度的谐波分析。因此，部分文献引入FFT或其他方法对信号先进行预处理。文献[4]提出了一种用于电力系统谐波分析的FFT-Adaline 算法, 并应用于整数次谐波的检测。文献[12]在文献[4]之上，提出将FFT与三角基线性网络结合用于间谐波的检测，并取得了较好的效果。文献[13]提出将同步挤压小波变换（SWT）与三角基Adaline网络结合，用于检测频率相近的谐波。文献[14]提出了使用最小均值M估计(LMM)对Adaline神经网络的权重进行自适应更新，具有良好的抗噪性能。文献[15]对FFT-三角基神经网络的结构、学习率、激励函数等参数进行改进，提高了该网络应对复杂信号的能力。文献[16]提出了一种独特的主从式自适应线性神经网络，并与传统的Adaline网络进行相比，误差更小，时间更短。文献[17]提出一种结合自适应线性神经网络和X滤波最小均方算法的谐波检测算法，该算法结构简单，并且收敛性快。

上述方法均取得了一定的效果，但仍存在一些问题。一是随着不同用电设备接入电网，电力系统谐波成分愈发复杂，系统中有很大可能含有频率相近的谐波成分，这些近谐波可能会引起灯具闪变等不良后果。传统方法虽然能检测出整数次谐波，但难以对这些相近谐波进行正确分析。如果忽略掉这些频率较近的谐波，很容易影响最终谐波参数辨识的准确度；二是在神经网络方法中，经过FFT（或其他方法）预处理的信号还需要人工判断谐波个数和频率，才能输入网络进行计算，这无疑增加了人的工作量，可能会导致由人主观判断引起的参数错误，自动化程度稍弱。

因此，针对上述问题，本文提出一种复调制频谱细化（Zoom-FFT）与Adaline网络结合的谐波检测方法。该方法分为细化部分和神经网络部分。细化部分中，使用复调制频谱细化对原始谐波信号进行预处理，利用峰值检测获取峰值处谐波大致频率。神经网络部分中，将获取的谐波频率代入动量因子改进的三角基函数网络，利用神经网络运算求解谐波准确的频率、幅值和相位。最后，通过仿真研究验证了所提出方法的有效性。

1 复调制频谱细化法

针对电力系统中存在频率较近的密集频率，一般来说通过常规的频谱分析难以判定谐波数量或者难以精确确定各谐波参数[18]。因此使用改进的复调制频谱细化法对频谱信号进行处理。复调制频谱细化就是将信号进行复调制移频，将准备深入分析的频带移动到中心零频率附近进行傅里叶变换的一种信号分析方法。

经典的复调制频谱细化的方法使用的是低通滤波器。但低通滤波器限制了整个频谱细化的准确度和细化的倍数，当细化倍数增大时，低通滤波器的边缘频谱可能会产生频谱的混叠[19]。因此使用复解析带通滤波器进行改进，构成带有复解析滤波器的复调制频率细化。图1展示了复解析滤波器由实际幅频特性移动到理想幅频特性的变化。

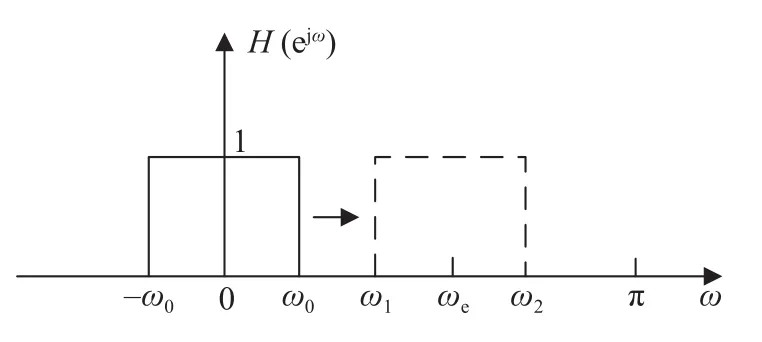
图1 复解析滤波器原理示意图

2 动量因子改进的三角基函数神经网络

对于一个含有谐波的电力系统电流信号，可以表示为：

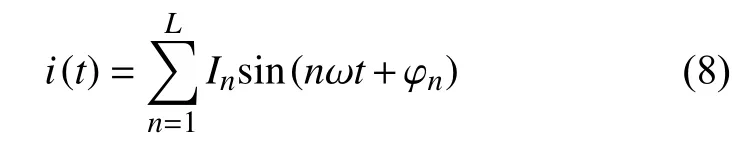
其中 ω=2πf，n为谐波/间谐波对应次数，In为第n个谐波的幅值，φn为第n个谐波的相位，L为总谐波个数。对上式的三角函数展开可得：

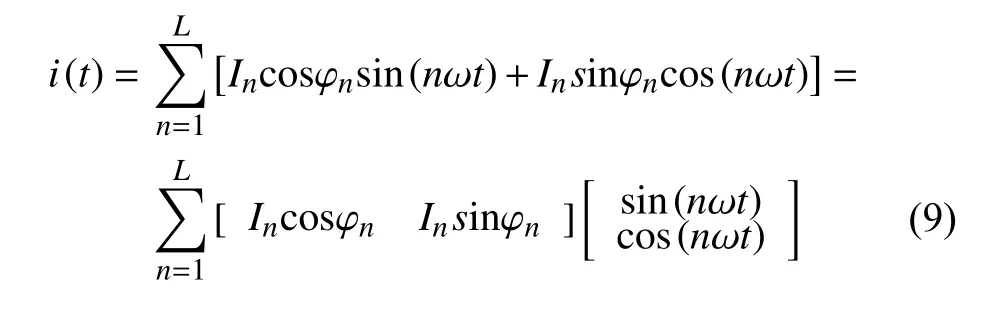
依据式(9)构造三角基函数神经网络（如图2所示），该网络与传统的BP神经网络结构和运算方式类似：网络为三层结构，包括一个输入层，一个输出层，和一个隐含层。各层的神经元个数比为1∶2L∶1，即输入层 1个神经元、输出层 1个、隐含层2L个神经元。运算方式包括前向传播和误差反向传播的两个过程，使用最速下降法调制各个层之间的权值，使用(cos, sin)的三角函数对作为其激励函数。该网络的调整过程如下：

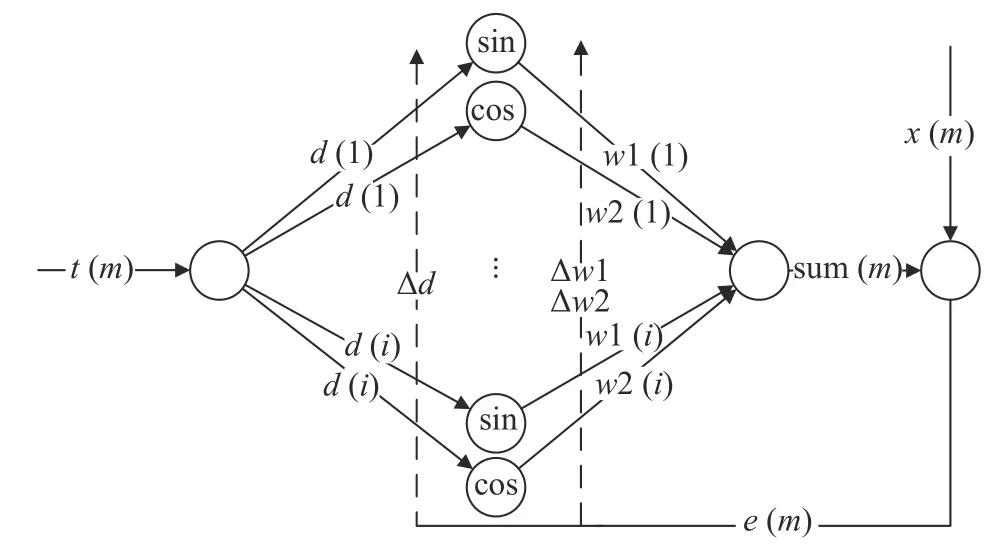
图2 三角基函数神经网络

3 算法流程

基于复解析滤波器复调制频谱细化法和三角基函数神经网络相结合的谐波检测方法的具体步骤，如图3所示。

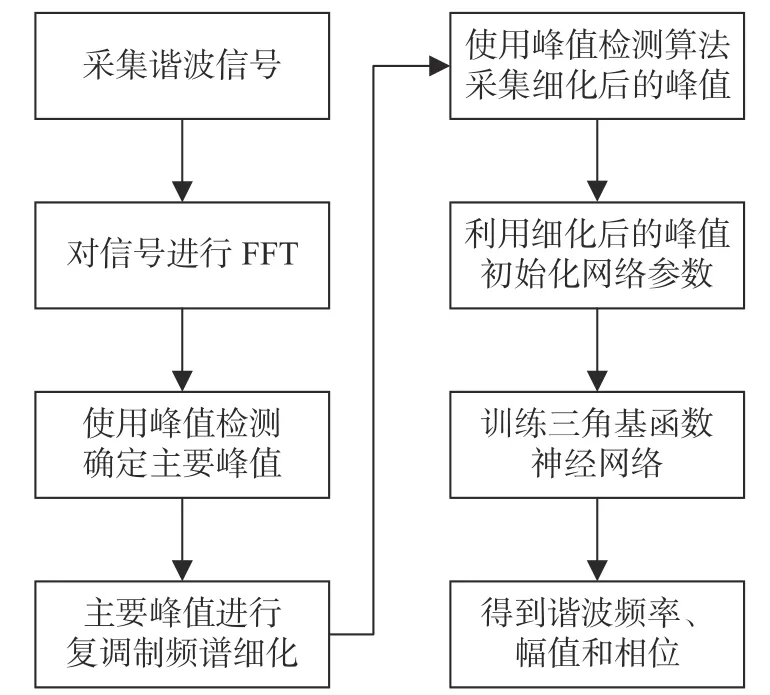
图3 算法流程

1）采集训练样本。确定信号的采样频率为fs,快速傅里叶变换长度为N，细化倍数为D，外扩系数a，按照式(7)计算得到滤波器的半阶数M。对谐波信号i(t)进行采样，得到i(n) (n=0, 1, 2, 3,···,DN+2M)。

2）对采样后的点进行快速傅里叶变换（FFT），得到该信号的频谱特性的曲线图。

3）根据步骤2）得到的频谱图，使用峰值检测算法找到图中的峰值对应的频率。

4）将步骤3）中得到的频率，作为复调制细化法的中心频率进行细化，有几个峰值就进行几次细化，并将细化过后的频带调整回实际频率处的频带，形成新的频谱图。

5）再次使用峰值识别算法统计新的频谱图峰值的个数和对应的频率，代入神经网络中作为输入层和隐含层之间的初始权值，输入神经网络中。

6）设定网络的循环次数、学习速率等可调量，使用神经网络进行运算，得到各个谐波分量的频率、幅值和相位。按照下式求得各个谐波/间谐波对应的频率Fi、幅值Ii和相位 φi。

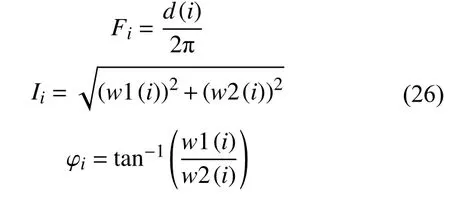
其中d代表输入层和隐含层之间的权值。

4 仿真验证

为了验证所提出的方法具有有效性和可行性，构造两组不同的算例样本进行仿真验证。

4.1 算例一

构造的电力系统谐波信号的频率、幅值和相位如表1所示。

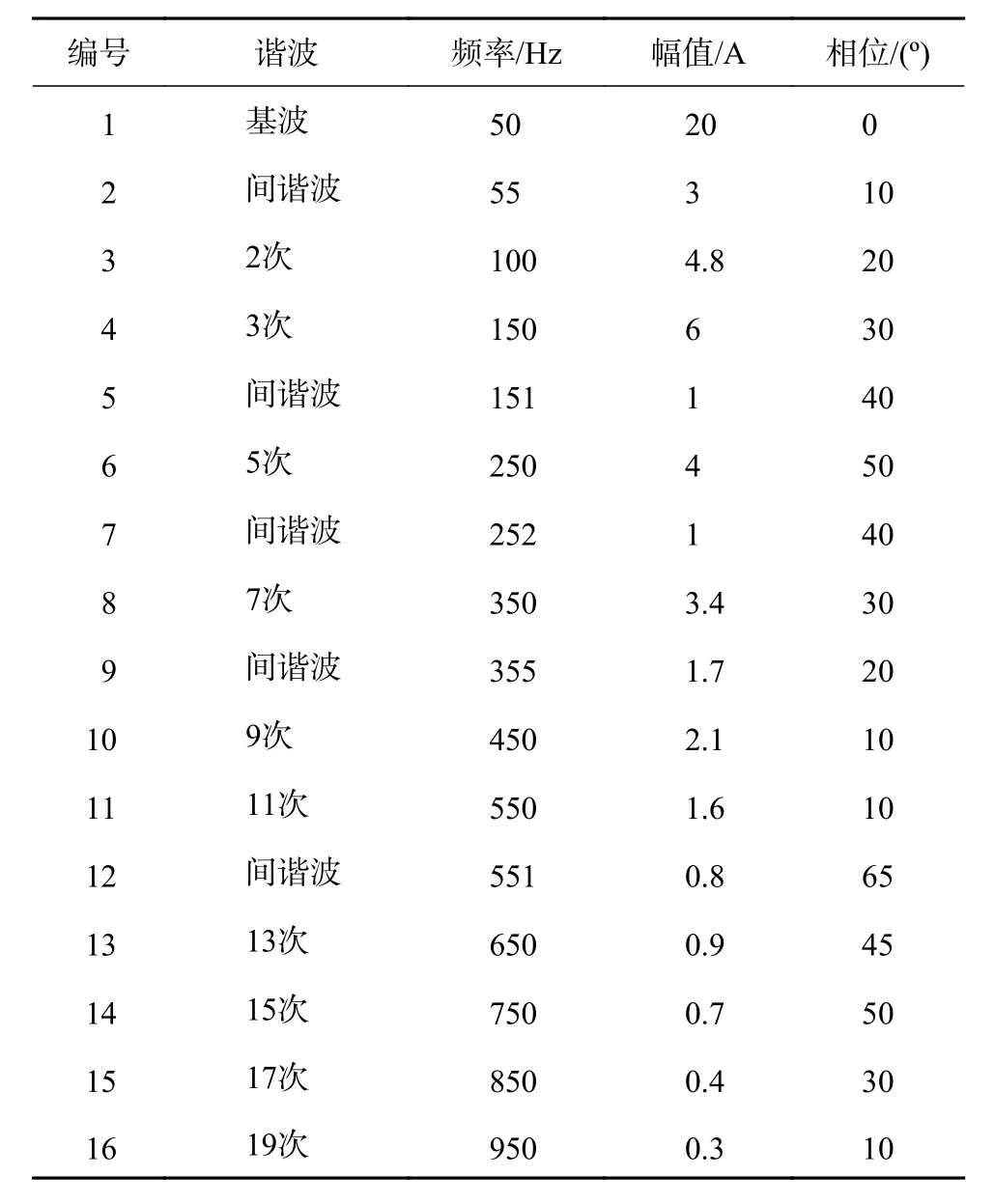
表1 算例信号参数设置

根据Shannon采样定理，快速傅里叶变换的采样频率应该大于两倍的最高频率，然而在工程上应用时，具体的谐波频率是未知的。根据国家标准GB/T 14549—1993《电能质量 公用电网谐波》[22]，测量的谐波次数一般为第2到第19次。因此，取采样频率为2 500 Hz。设置采样点数为400，傅里叶变换长度为40，可以得到图4所示曲线。从图4可以看出，峰值的个数约为6，分别对应的62.5 Hz、250 Hz、375 Hz、562.5 Hz、750 Hz、937.5 Hz，且对应的幅值也与设定的谐波幅值有较大出入。如果此时按照6个峰值个数来进行后续的神经网络运算，难以使得神经网络的准确度收敛到较为准确的结果，并且从工程上来说，难以对此类复杂且谐波成分不明确的间谐波进行有效的谐波治理。

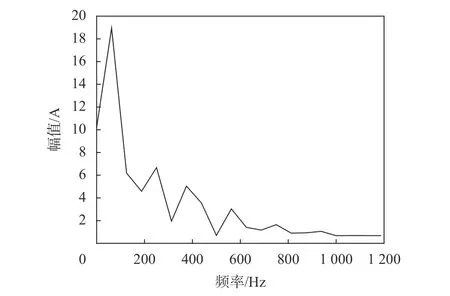
图4 快速傅里叶变换后的频谱

因此，针对上述问题，应用所提方法加以改进，组合使用复调制细化和神经网络对信号进行处理。根据步骤首先确定复调制细化的采样点数。设置采样频率fs为2 500 Hz，抽选比D为100，外扩系数a为0.3，得到最终的采样点数为ND+2M。其中M是滤波器半阶数，按照式(7)求出，并对上述步骤得到的离散谐波信号进行快速傅里叶变换。

细化前后的频谱对比如图5所示。图5（a）为细化前的频谱。可以看出，图5（a）中的频谱相对图4已经较为明确，但对于频率相近的成分仍然难以区分，需要使用细化法进一步分析。复调制细化法需要确定分析的中心位置才能进行较为细致地分析，而峰值处对应的较小频率区间是密集频谱的主要位置。因此需要对峰值周围进行分析。确定峰值的方法有很多，如奇偶拐点高斯分解法、“findpeaks”函数法等等。使用的确定峰值的方法是 “findpeaks”函数。“findpeaks”是Matlab中自带的函数，能够较为准确地探测波形的峰值，其主要原理是利用波形某一侧的值与左右相邻两侧指定个数的值进行对比[23]若是该点的值大于左右相邻的点的值，则为峰值点。设置最低峰值高度为0.01 A，在一定程度上消除噪声的影响。经过“findpeaks”函数的检测，可以识别出图5（a）中的峰值个数为13。

图5 频谱细化前后对比

将检测出来的这13个峰值对应频率分别作为复调制细化法的中心频率，进行细化，可得到图5（b）。图5（b）展示了细化后的频谱分布。经过上述的细化过程后，整个曲线能精确的反映出谐波的个数以及大致频率。以图5（a）中第四个峰值为例进行分析，图6展示了第四个峰值细化前后的对比，其中虚线是细化前的峰值，实线是细化后的峰值。可以看出，细化前频率为150 Hz左右的峰值可以细化为两个频率在150 Hz附近的峰值，这体现了该方法能够分离出密集频谱的能力。此时对图5（b）再次使用“findpeaks”函数并设置最低峰值高度为0.01 A，进行峰值检测，可以自动检测出16个对应的峰值，其对应的频率较细化前的准确度有较大提升，与实际设定的频率十分接近。但很难用肉眼识别，这在一定程度上体现了本方法具有较好的自动化水平。

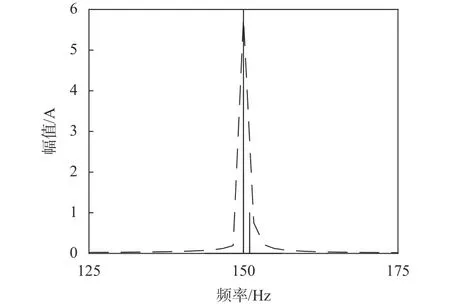
图6 250 Hz处峰值

通过神经网络进一步提高频率和幅值的准确度，并求出精确的幅值、相位和频率。利用峰值检测算法得到的频率个数为16，对应神经网络的隐含层个数的2倍；利用峰值对应的频率大小生成神经网络的输入层和隐含层的初始权值。网络的结构为1—32（2倍峰值个数）—1。由于细化过后的频率已经接近真实值，故此时只需取较少的数据样本代入网络，即可得到较为准确的结果。取快速傅里叶变换时采集的前400个点，作为网络每次循环的输入数据集。设定最大的迭代次数为200次，预设准确度为10-9。参考文献[24]中的相位和幅值的学习率为 0.016 5，频率学习率为 1.65×10-8，动量因子a=0.5。共经过0.5 s的运算，得到该信号的频率、相位和幅值，与真实值的对比如表2所示。图7展示了神经网络的误差下降情况。较快下降的误差，体现了神经网络较好的收敛效果。

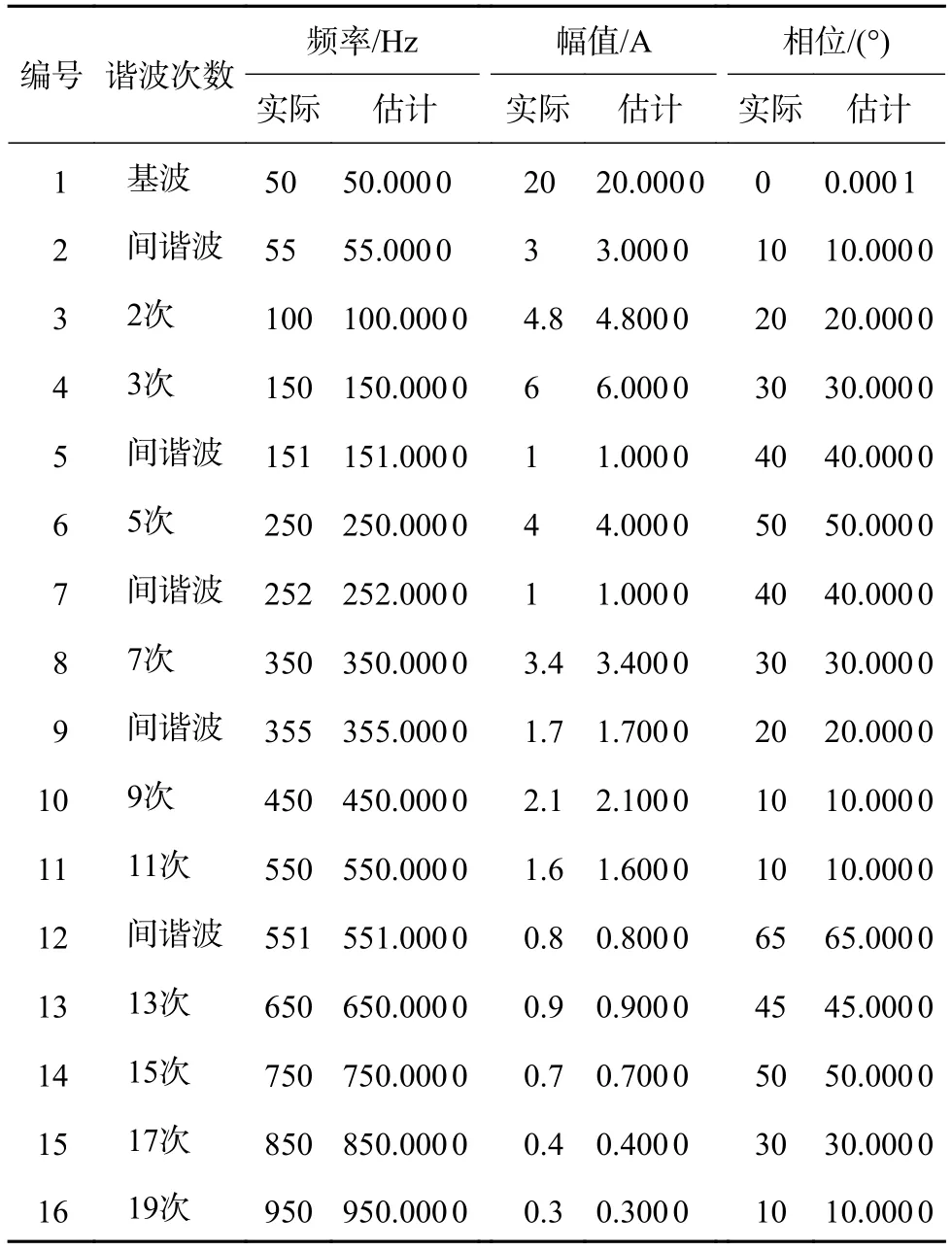
表2 所提算法估计值与真实值的对比

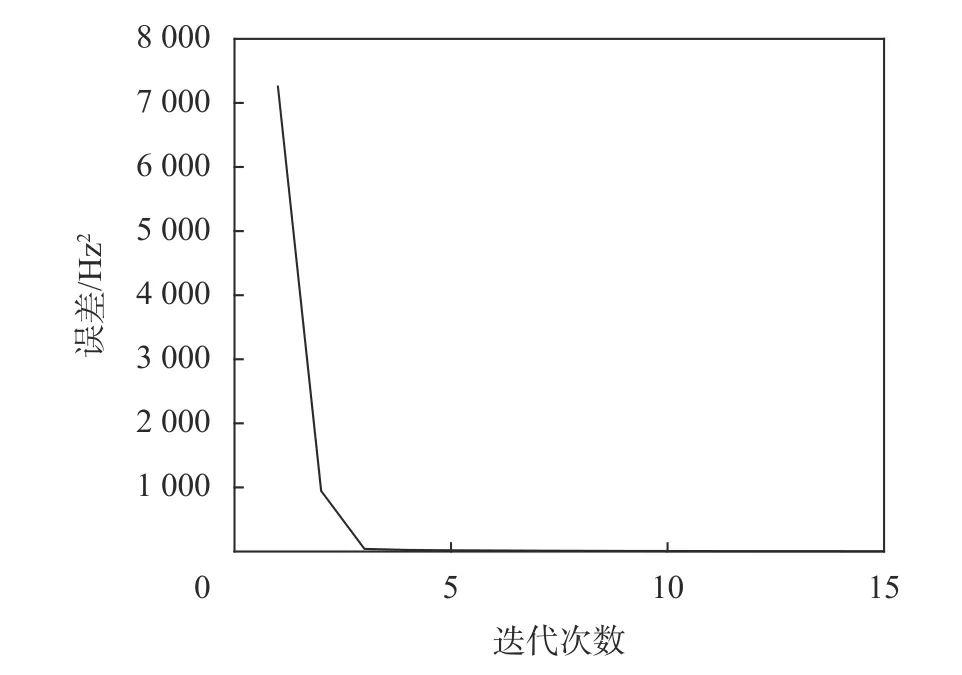
图7 神经网络的误差曲线

4.2 算例二

采用文献[25]的数据进行对比。文献[25]提出采用多谱线插值法测量频率较远的谐波，而采用带有复解析滤波器的复调制细化法测量较近的谐波。将文献[25]的仿真信号代入文中方法，进行对比。设置采样频率fs为2 500 Hz，快速傅里叶变换长度为1 500，抽选比D为100，外扩系数a为0.3。表3展示了两种方法与真实值的对比结果，可以看出所提方法谐波参数辨识结果比[25]更为准确。

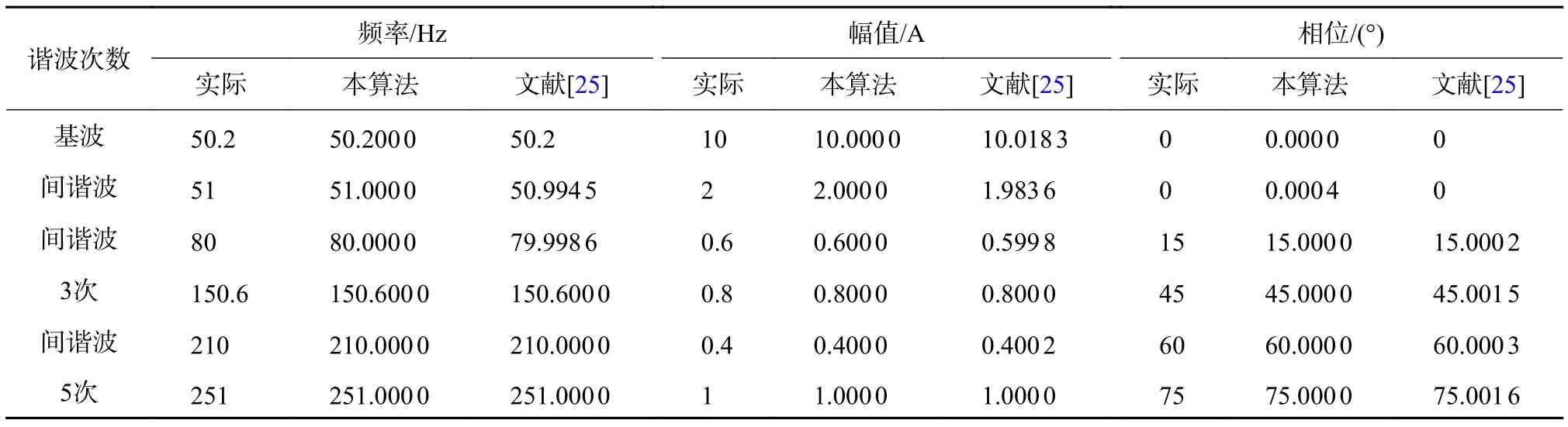
表3 所提算法与文献[25]的结果对比

4.3 讨论

根据谐波测量相关的国家标准[22-26]，对频率测量仪器的误差要求不能超过±0.01 Hz；负荷变化较快的谐波源测量的时间不大于2 min。且规定A级仪器频率测量范围为0～2 500 Hz，用于较精确的测量，仪器的相角测量误差不大于±5°或±1°。从表2、表3可以看出，使用所提算法准确度较高，达到了小数点后三位，符合相关标准要求。

所提出算法有如下特点：1）复调制细化分析具有一定优势。一方面，复调制的方法对特定频率的附近频带进行细化，可以分辨出频谱相近的间谐波（从图6可以看出）。另一方面，经过细化后的频率也更加接近谐波信号的真实频率，使得神经网络的收敛更为迅速；2）通过“findpeaks”函数（或其他类似的数学方法）识别峰值，并设定了峰值识别的最小值，从某种意义上来说消除了一定的白噪声的影响，并减少了人工识别可能造成的漏识或错识，它们可能会使得网络难以收敛到误差范围内，影响最终结果的准确程度；3）在准确度较高的情况下，运算时间短。经过细化后得到的频率更加接近频率的真实值，因此在神经网络运算时，设置较少的输入数据和较少的循环次数就能达到较好的检测效果，并且运算时间较短，算例一中对19次谐波进行检测，总用时仅为0.9 s左右。

本方法也存在一些不足和值得改进的地方：1）本方法对采样长度的要求较为严格，复调制细化分析法的采样点数要求为DN+2M，远大于一般的采样时间，难以做到现场采样现场分析，适合化工整流器、直流输电换流站等变化较慢的谐波源[22]。未来可以考虑在长期固定的电力监测系统中使用；2）峰值识别算法识别精确度的也影响总体算法的准确度，峰值识别算法有很多种，只是选取Matlab中的“findpeaks”函数进行识别。未来，随着计算能力的提升，是否还有更好的方法（如图像识别）来进行峰值辨识，且速度上能否比快速傅里叶快，还是一个值得探索的问题。

5 结束语

本文针对传统FFT-Adaline方法中，存在快速傅里叶变换过程后难以识别相近频率的问题，提出了一种复调制细化法和识别峰值算法相结合的改进方法。该方法利用改进的复调制细化法对快速傅里叶变换中的峰值，进行细化，得到更为细致的频谱图，获得新峰值的个数和相近频率，输入到Adaline网络进行训练。结果表明，该方法可以有效的解决次数相近的谐波精细化辨识的问题，对整数次谐波、非整数次谐波和频率相近谐波的参数均能正确辨识，准确度较高且时效性较好。然而本方法对采样数据的要求较为严格，下一步研究可以对此展开。