气体静压小孔节流焦耳-汤姆逊效应的测试研究
2022-06-10李东升尹健龙沈小燕
程 楼,禹 静,李东升,罗 钦,尹健龙,沈小燕
(中国计量大学计量测试工程学院,浙江 杭州 310018)
0 引 言
在超精密加工及超精密检测技术领域中,气体静压润滑节流技术相较于传统滚动轴承和油、脂滑动轴承技术相比,具有精度高、速度快、爬行小、无污染或者少污染、结构简单等优点[1-3]。在一般工程中,由于精度要求不是特别高,所以采用都是近似计算会忽略焦耳-汤姆逊效应所造成参数变化,但依然可以满足要求。然而在高精密应用的场合,考虑由焦耳—汤姆逊效应所造成的参数变化对于节流器性能的影响,就十分必要了。付坤霞等[4]建立了存在温度影响的空气静压轴承润滑模型,并计算出轴承变形量可以达到 7 .4%。但并没有对节流过程建立理论模型。程阳等[5]通过4个经典状态方程计算空气的焦耳-汤姆逊系数,并确定最合适的状态方程;邓成香等[6]分别利用4个经典状态方程计算氢气、氮气、空气和二氧化碳的焦耳-汤姆逊系数并进行纵向对比,为每种气体选择最佳的状态方程。但他们研究都只是应用在简单的小孔节流上,并没有将焦耳-汤姆逊效应应用在如气体静压节流技术等实际的工程技术当中。
本文通过以焦耳-汤姆逊效应作为切入点建立了节流器的小孔节流温降与压降理论模型,通过实验验证理论模型的准确性。
1 气体静压节流焦耳-汤姆逊效应
气体静压节流基本原理:高压气体在流入节流器后会先经过节流过程,然后在润滑过程中形成润滑气膜,最后进入大气。
节流过程中气体在经过一个狭窄通道后,由于焦耳-汤姆逊效应的作用气体压强会从供气压强ps降至节流孔出口压强pd,与此同时气体温度也会随之变化。并且温降与压降分别满足以下公式:
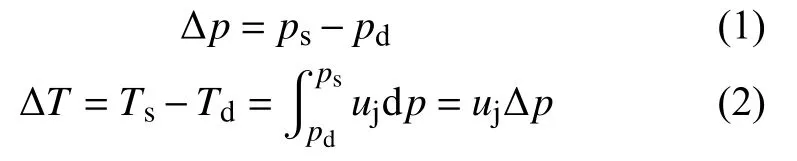
式中: ΔT——进出口温降;
Δp——进出口压降;
ps——供气压强;
Ts——供气温度;
pd——节流孔出口压强;
Td——节流孔出口温度;
uj— —焦耳-汤姆逊系数。
从式(1)和式(2)中可以看出,求解节流前后的温降 ΔT与压降 Δp,需要得到焦耳-汤姆逊系数uj,供气压强ps与节流孔出口压强pd。空气的焦耳-汤姆逊系数uj通 过SRK状态方程求得,供气压强ps是已知量,节流孔出口压强pd需要特别计算。
计算pd需要利用气体在润滑过程中满足雷诺方程这一特性。因此求解润滑气膜的雷诺方程是分析气体静压节流焦耳-汤姆逊效应前提。
1.1 雷诺方程的求解
润滑气膜非等温定常多变过程的雷诺方程:
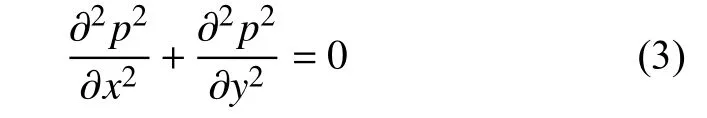
目前,有很多数值计算的方式求解雷诺方程,本文使用有限差分法求解雷诺方程[7]。
首先需要对节流器的气膜区域网格划分。由于本文中涉及到的节流器相对简单,采用等距网格划分方法,如图1所示。对x和y方向分别进行n、m等分,产生n+1、m+1个节点,整个气膜区域共产生(n+1)×(m+1)个节点。
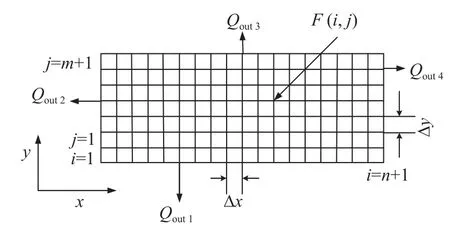
图1 气膜区域网格划分图
图1中,F表示气膜中各节点处压强的平方。根据差分原理与雷诺方程,气膜中的任意一个节点F(i,j)都可以表示为:
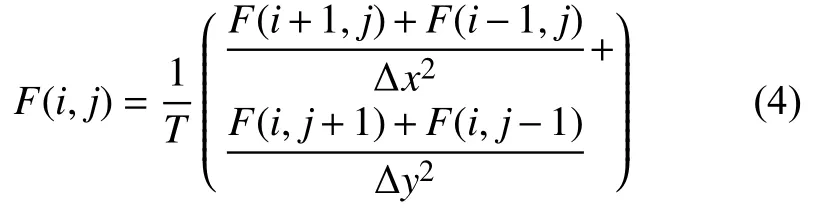
首先设定边界条件并将各个节点赋初值,代入公式(4)计算出F1(i,j)和F2(i,j)后采用超松弛迭代的方法,根据式(5)计算Fr+2(i,j)(r=1,2,3,···):
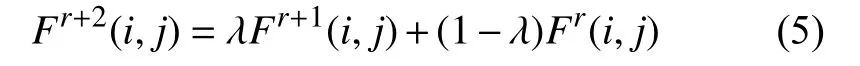
上式中 λ为加速系数,取值范围为1 <λ<2。
当满足收敛条件式(6)后结束运算,得到润滑气膜的压强分布。
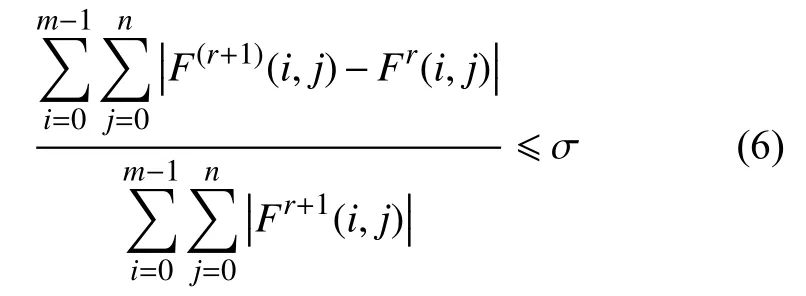
最后通过进出口流量守恒定理即流入润滑气膜的流量Qin等于流出气膜的流量Qout,如果两者相差过大则调节流孔出口压强pd重新代入公式(4)进行再次进行迭代运算,直至 |1 -Qin/Qout|≤ε(ε为一个极小的值)[8-11]。
经过上述步骤后就可以得到一个准确的pd,将其代入公式(2)中得到 ΔT。
利用上述控制方程进行求解的流程图如图2所示。
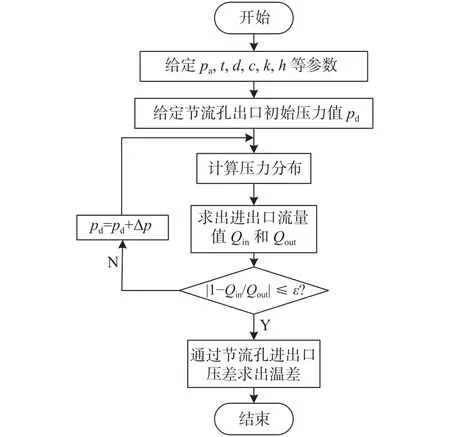
图2 计算流程图
1.2 进出口压降的理论计算
利用Matlab对100 mm×60 mm双U形节流器(大双 U)、90 mm×60 mm双环形节流器 (双环)与60 mm×30 mm双U形节流器(小双U)的节流孔进出口温降与压降进行了数值计算。本文主要计算的是供气压强为 0.3~0.5 MPa、气膜厚度为 5~15 μm时节流孔进出口温降与压降的变化曲线。
其中在气膜厚度为10 μm的条件下,计算所得到的进出口压降Δp随 供气压强ps变化曲线如图3所示。
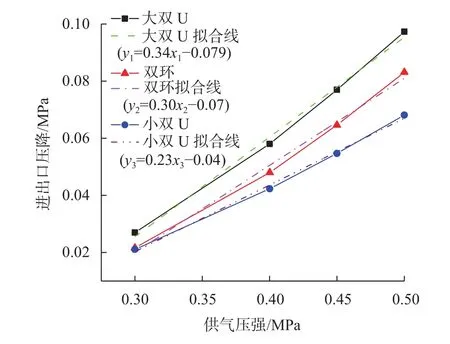
图3 进出口压降Δp与 供气压强ps的理论关系图
图3所示,大尺寸节流器的压降大于小尺寸节流器的压降,而在节流器尺寸相近的情况下大双U的压降大于双环的压降;并且三种节流器进出口压降与供气压强都是线性正相关,经过直线拟合后发现其斜率都在0.2~0.4之间。
其中在供气压强为0.5 MPa的条件下,计算所得到的进出口压降Δp随 气膜厚度h变化曲线如图4所示。
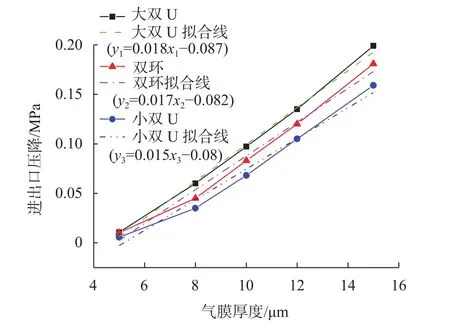
图4 进出口压降Δp与气膜厚度h的理论关系图
图4所示,大尺寸节流器的压降大于小尺寸节流器的压降,而在节流器尺寸相近的情况下大双U的压降大于双环的压降;并且三种节流器进出口压降与气膜厚度都是线性正相关,经过直线拟合后发现其斜率都在0.01~0.02之间。
1.3 进出口温降的理论计算
其中在气膜厚度为10 μm的条件下,计算所得到的进出口温降 ΔT随进口压强ps变化曲线如图5所示。
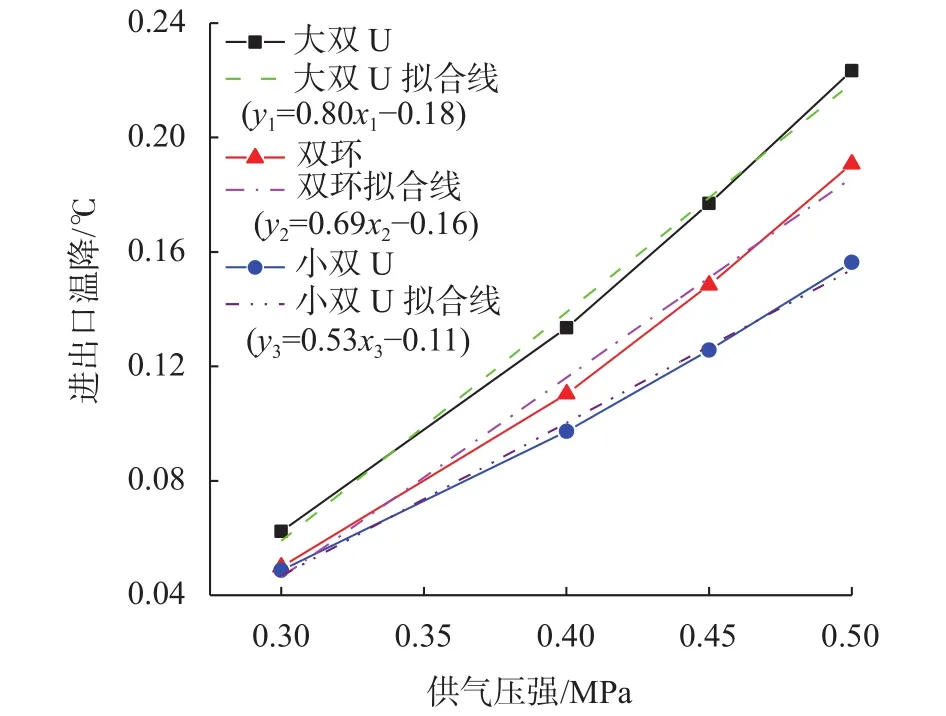
图5 进出口温降 ΔT与供气压强ps的理论关系图
图5所示,大尺寸节流器的压降大于小尺寸节流器的温降,而在节流器尺寸相近的情况下大双U的温降大于双环的温降;并且三种节流器进出口温降与供气压强都是线性正相关,经过直线拟合后发现其斜率都在0.6~0.8之间。
其中在供气压强为0.5 MPa的条件下,计算所得到的进出口温降 ΔT随气膜厚度h变化曲线见图6。
图6所示,大尺寸节流器的温降大于小尺寸节流器的温降,而在节流器尺寸相近的情况下大双U的温降大于双环的温降;并且三种节流器进出口温降与气膜厚度都是线性正相关,经过直线拟合后发现其斜率都在0.03~0.05之间。
2 压差实验
2.1 测量实验设备
本次实验所使用实验装置,如图7所示。
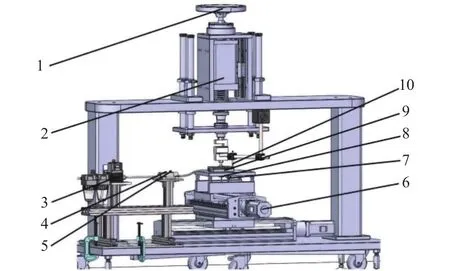
图7 实验设备图
本实验装置通过转动调节手轮控制中心体的上下移动进而做到稳定节流器并调节气膜厚度[12];通过电气调节阀来调节供气压强;通过传感器测量节流器进出口压强与温度。
2.2 供气压强对于进出口压降的影响
利用上述实验装置,对供气压强在0.3~0.5 MPa、气膜厚度在5~15 μm范围内三种节流器的进出口压降进行了测量。
其中在气膜厚度为10 μm的条件下,实验所得到的进出口压降Δp随 供气压强ps变化曲线如图8所示。
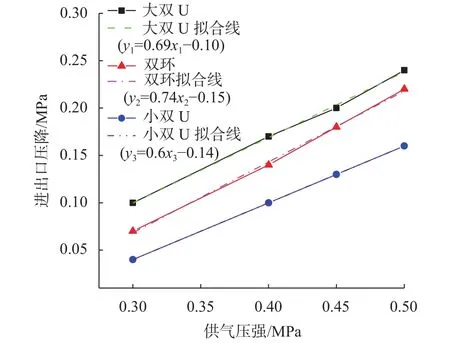
图8 进出口压降Δp与 供气压强p s的实验关系图
图8所示,大尺寸节流器的压降大于小尺寸节流器的压降,而在节流器尺寸相近的情况下大双U的压降大于双环的压降;并且三种节流器进出口压降与供气压强都是线性正相关,经过直线拟合后发现其斜率都在0.6~0.8之间。
2.3 气膜厚度对于进出口压降的影响
其中在供气压强为0.5 MPa的条件下,实验所得到的进出口压降Δp随 气膜厚度h变化曲线如图9所示。
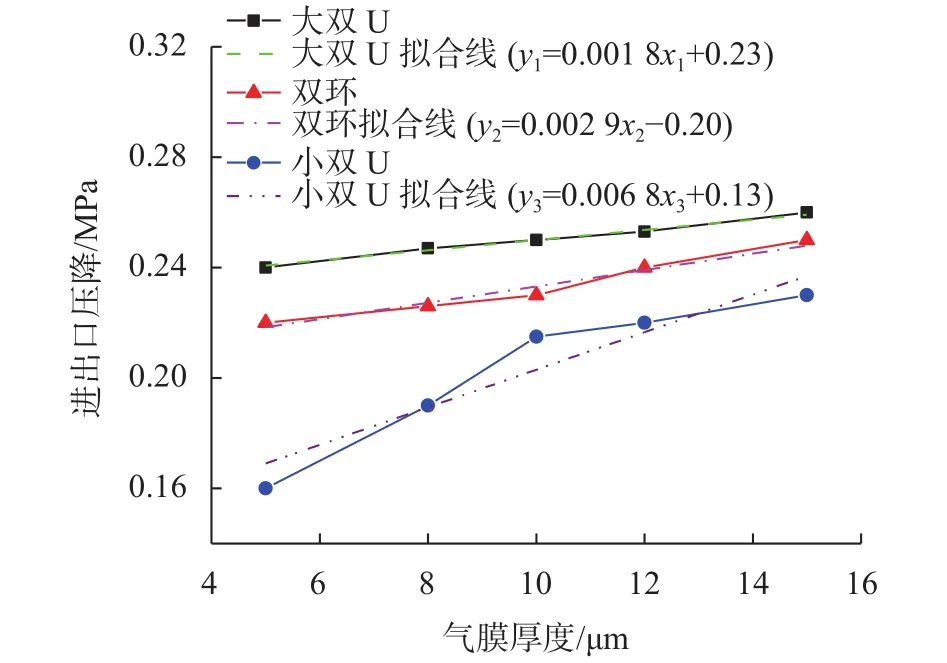
图9 进出口压降Δp与气膜厚度h的实验关系图
图9所示,大尺寸节流器的压降大于小尺寸节流器的压降,在节流器尺寸相近的情况下大双U的压降大于双环的压降;并且三种节流器进出口压降与气膜厚度都是线性正相关,经过直线拟合后发现其斜率都在0.002~0.007之间。
3 温差实验
3.1 供气压强对于进出口温降的影响
利用上述实验装置,对供气压强在0.3~0.5 MPa,气膜厚度在5~15 μm范围内三种节流器的节流孔进出口温降进行了测量。
其中在气膜厚度为10 μm的条件下,实验所得到的进出口压温降 ΔT随供气压强ps变化曲线如图10所示。
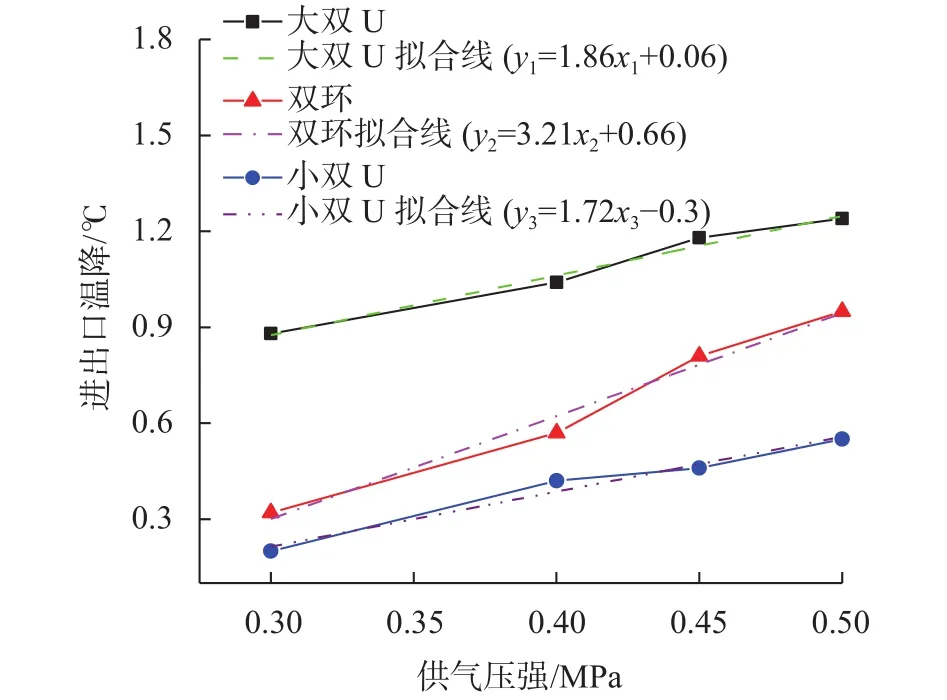
图10 进出口温降 ΔT与供气压强ps的实验关系图
图10所示,大尺寸节流器的温降大于小尺寸节流器的温降,而在节流器尺寸相近的情况下大双U的温降大于双环的温降;并且三种节流器进出口温降与供气压强都是线性正相关,经过直线拟合后发现其斜率都在1.5~3.2之间。
3.2 气膜厚度对于进出口温降的影响
其中在供气压强为0.5 MPa的条件下,实验所得到的进出口温降 ΔT随气膜厚度h变化曲线如图11所示。
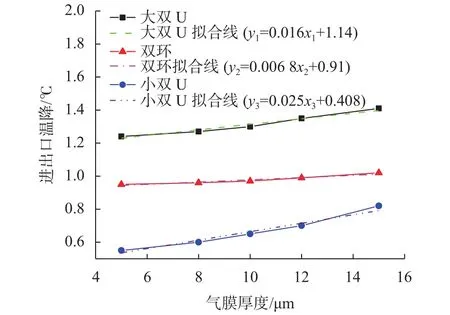
图11 进出口温降 ΔT与气膜厚度h的实验关系图
图11所示,大尺寸节流器的温降大于小尺寸节流器的温降,而在节流器尺寸相近的情况下大双U的温降大于双环的温降;并且三种节流器进出口温降与气膜厚度都是线性正相关,经过直线拟合后发现其斜率都在0.006~0.03之间。
实验与理论计算之间存在差异的主要原因:1)将实际气体看成不可压缩的气体这一假设本身就会含有一定的误差;2)在理论计算中忽略了节流器润滑气膜在流动过程中与表面产生摩擦所产生的压损;3)在利用有限元差分法进行数值计算过程中,网格划分和迭代精度选择的不同会对计算结果精度产生一定的影响;4)实验装置会使实验的环境温度不稳定,使得节流器的温降测量存在一定偏差。
4 结束语
通过以焦耳-汤姆逊效应作为切入点,研究了节流器小孔节流的温降与压降,建立了双环形节流器、大双U形节流器与小双U形节流器的小孔节流温降与压降理论模型,进行了理论计算,并通过实验进行了验证,发现:理论压降与实验压降在气膜厚度、进气口压强的相关性上具有一致性;理论温降与实验温降在气膜厚度、进气口压强的相关性上具有一致性;理论与实验都存在大尺寸节流器的温降与压降大于小尺寸节流器的温降与压降,在节流器尺寸相近的情况下双U的温降与压降大于双环的温降与压降这一特点;理论和实验都表明相对于气膜厚度而言供气压强对进出口参数的影响更大。说明了理论模型的准确性,为节流器节流孔的设计以及供气压强与气膜厚度的选择提供了理论基础。
