球窝型总压探针气动结构选型分析研究

王玉芳，董素艳，荆卓寅，赵 俭

(1. 中国航空工业集团有限公司北京长城计量测试技术研究所，北京 100095; 2. 西北工业大学，陕西 西安 710072)

0 引 言

作为接触式测量方法，总压探针凭借其方便、可靠的特点在航空航天气动流场测量领域有着非常广泛的应用。目前常用的总压探针有三种结构形式，分别为L型探针、带套筒型探针以及球窝型探针[1]。这三种结构总压探针其特点各不相同，其中L型探针结构简单，但不敏感角度小；带套筒型探针测量性能优于L型，但其结构较为复杂，尤其套筒直径相对较大，增大了其使用安装不便性；球窝型探针测量性能相对其他两种最佳，且结构简单便于安装，唯一的缺点是对加工精度要求较高。随着这些年机械加工技术的发展，球窝型压力探针的缺点被大大减小，其整体的实用性有着显著提高[2-4]。

Zilliac[5]和Timothy[6]通过一种新的压力探针结构的通用分析模型，并通过将其与三孔偏航坐标方法和七孔探针的实验测量校准数据进行比较，证明了该模型的有效性可应用于压力探针在气动流场测量中的校准。Saravana[7]采用不同的湍流模型对S管道的对应测点位置总压恢复参数进行仿真计算，并对比流场内是否加总压探针的仿真计算，结果表明，采用k-omega湍流模型仿真计算得到的总压恢复系数与实验值比较接近；同时，流域内添加总压探针模型与不添加探针模型相比仿真结果更为可靠。沈天荣[8]等采用不转动法校准L型七孔压力探针，对校准结果进行分析，发现对于大部分校准点通过插值算法得到测量结果与真实值比较一致误差范围不超过0.5%。马宏伟[9]等研究了速度梯度、近壁效应和雷诺数对压力探针测量误差的影响，结果表明，横向梯度能引起偏转角测量误差;纵向梯度能引起俯仰角测量误差；梯度使气流方向测量值向负梯度方向偏转。圆柱探针和锥形多孔探针相比，气流方向测量误差对速度梯度更敏感，纵向梯度对俯仰角测量值的影响尤其大。赵彬[10]等对超音速下总压探针进行数值仿真研究，总压探针位置、压力、马赫数等几个关键参数对总压恢复系数的影响规律，并与实验结果进行对比，结果表明安装位置对总压探针的恢复系数影响最大，探针越靠近试验段前方，总压系数绝对值越小。郑光华[11]等基于计算流体力学方法，研究了两种不同结构形式(单点、四点梳状)的总压探针对被测流场及自身总压测量值造成的影响差异。结果表明随着堵塞比的增大，各测点的总压测量误差增大；随着马赫数的增大，各测点的总压测量误差增大。Bubeck[12-13]等通过对球窝五孔探针的试验研究，发现该类型探针在近壁端测量时发现近壁测量时探针的俯仰角测量值存在误差，偏离值为5°。陈金华[14]研究了超音速流场中影响总压探针角度特性的因素及其影响规律，结果表明对于圆柱外形带圆锥内腔的总压探针，其内腔半锥角越小，敏感角度越大。冷旭明[15]等研究了总压管对超音速流场结构的影响，并得到了利用总压管测量超音速自由射流流场结构时，在一定区域内误差较小，但在超音速向亚声速过渡的区域内误差却较大的结论。

综上所述，总压探针的测量准确性对于获得流场相关参数至关重要。在实际测量过程中，由于安装误差或无法确定的气流来流方向，使得气流不敏感角对总压探针的测量误差产生重要的影响。本文依据气动压力探针的传统设计方法，同时，结合计算流体力学方法，对球窝型压力探针进行结构优化设计研究，并通过风洞实验对优化设计方案进行验证，研究出适合于工程实际应用的最佳球窝型压力探针结构方案。

1 结构优化方案

1.1 方案1——球窝型标准结构

球窝型总压探针标准结构如图1所示。其中，球窝半径R和套管直径D满足R/D= 0.4～0.6的球窝设计要求，一方面，避免球窝尺寸过小，测量过程效果不明显，另一方面，避免球窝尺寸太大，测量结果受圆柱绕流的流场影响。球窝球心到支杆端头的距离h应满足h＞2D设计要求，以避免支杆端头对球窝附近流场的影响。套管壁厚设计为c=（2/3）R，并将感压孔开在支杆上，由于没有突出部分，安装尺寸较小，同时也改善了机械强度。具体结构尺寸，球窝内径：3 mm；孔口内径：2 mm；管壁厚度：2 mm；球窝球心到支杆端头距离：6 mm；套管直径：6 mm。

1.2 方案2——球窝型偏心小内径结构

方案2结构在方案1标准结构的基础上，减小孔口内径为其1/2，同时将支杆内孔设计为偏心结构，主要为探究孔口尺寸以及偏心结构对不同敏感角下球窝附近流场的影响及测量偏差规律。具体结构尺寸如图2所示，球窝内径：3 mm；孔口内径：1 mm；球窝球心到支杆端头距离：6mm；套管直径：6 mm。

图2 球窝型偏心小直径结构

1.3 方案3——球窝型两侧削平结构

方案3结构在方案1标准结构的基础上，对球窝至支杆头部的圆柱两侧面进行削平处理，切削深度为1 mm，主要为探究球窝附近非圆柱绕流流场情况对不同不敏感角下总压探针的测量误差影响规律。同时，考虑削平两侧圆柱杆后探针的机械强度，减小其内孔孔径，增大球窝至支杆头部的管壁厚度。具体结构尺寸如图3所示，球窝内径：3 mm；孔口内径：1 mm；切削深度：1 mm；球窝球心到支杆端头距离：6 mm；套管直径：6 mm。

图3 球窝型两侧削平结构

1.4 方案4——直孔型3 mm孔径结构

方案4结构针对方案1标准结构，改变球窝型结构方式为直孔型，同时孔径改为3 mm。由于标准结构其球窝结构在加工过程中难以精确控制，满足要求的成品率较低，因此，该结构设计主要目的是考虑降低加工过程的复杂度。具体结构尺寸如图4所示，直孔内径：3 mm; 孔口内径：1 mm；切削深度：1 mm；直孔中心到支杆端头距离：6 mm；套管直径：6 mm。

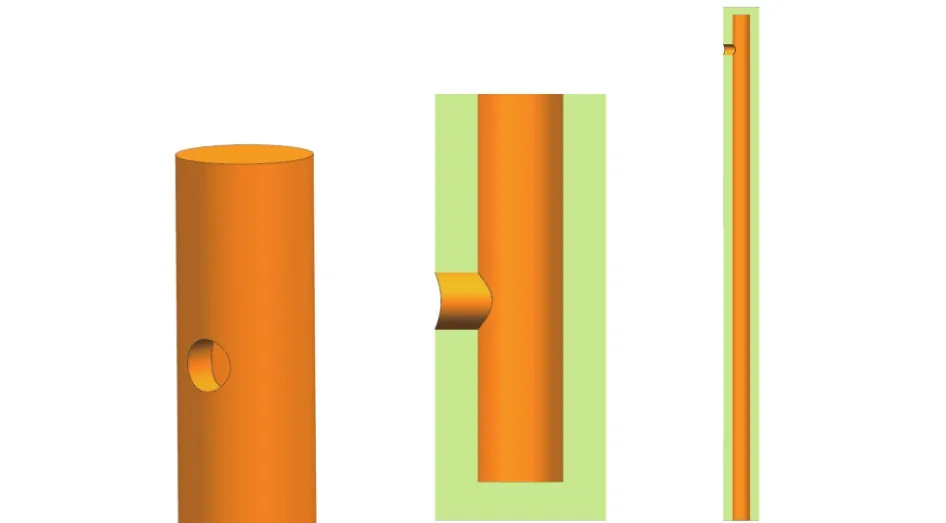
图4 直孔型3 mm孔径结构

1.5 方案5——直孔型4 mm孔径结构

方案5结构在方案4的基础上改变孔径为4 mm。具体结构尺寸如图5所示，直孔内径：3 mm；孔口内径：1 mm；切削深度：1 mm；直孔中心到支杆端头距离：6 mm；套管直径：6 mm。

图5 直孔型4 mm孔径结构

2 数值仿真方法

2.1 计算域

五种结构的总压探针仿真计算，除结构尺寸不同外，计算域及计算工况完全相同，计算域如图6所示，整个计算域的设定截取实际实验室常温风洞的对应测试流域。

图6 流场仿真计算域

2.2 网格划分

本文采用多面体网格划分，多面体网格在保证相同计算精度的同时，其网格数量相比较四面体或混合网格少3～5倍，从而使数值计算解收敛更快，并且节省计算资源；同时，对总压探针壁面以及周围流场进行网格加密如图7所示，网格最小尺寸为0.04 mm，网格最大尺寸为6.00 mm。对总压探针壁面处划分边界层，边界层层数为7层，生成网格的总数量约为600万，整体流域截面网格示意图如图8所示。

图7 总压探针网格加密展示

图8 总压探针整体流域截面网格展示

2.3 数值求解方法

本文中湍流模型采用Realizable k-e Model。主要考虑以下方面：该模型对较强压力梯度、圆柱绕流等问题计算精度更好；同时，本数值模拟亚音速流速，流动介质为理想空气，因此，湍流模型中考虑可压缩性影响。由于可压缩流动，其速度、密度、压力及能量之间的高度耦合，一方面耦合会导致解的不稳定性，同时，计算低马赫数条件下可压缩流动易引入过大的截断误差，综合考虑以上问题，该数值模拟过程采用以下离散格式：梯度基于单元体的最小二乘法差值格式；压力、密度、动量、湍动能、湍耗散率、能量的离散方法均采用二阶迎风格式，主要考虑低阶格式带来过大截断误差的缺点。采用SIMPLE半隐式格式求解。

2.4 计算工况

总压探针计算边界条件：环境温度：300.0 K；来流马赫数：0.42；来流总压：13 073.15 Pa；参考压强：101 325.00 Pa。

由于在数值仿真中不存在安装误差，气流与模型正方向偏15°，与偏–15°两种情况完全对称，因此，实际仿真时仅考虑其中一种情况：气流与模型正方向偏15°。在此基础上，建立以下6个计算工况来探究球窝型压力探针设计的最佳优化方案：

case 0：球窝型标准结构，气流方向与模型正方向偏 0°；

case 1：球窝型标准结构，气流方向与模型正方向偏 15°；

case 2：球窝型偏心小内径结构，气流方向与模型正方向偏15°；

case 3：球窝型两侧削平结构，气流方向与模型正方向偏15°；

case 4：直孔型孔径3mm结构，气流方向与模型正方向偏15°；

case 5：直孔型孔径4mm结构，气流方向与模型正方向偏15°。

3 试验验证

3.1 试验系统

如图9为北京长城计量测试研究所国家重点实验室低速风洞示意图，主要包括离心式风机、压力传感器、数字无汞气压计、数采模块、压力扫描阀等设备。离心式风机把周围空气抽到气罐中，然后经过入流管道给试验段供气。入流空气首先进入稳定段内，然后经过收缩段，流入试验段。

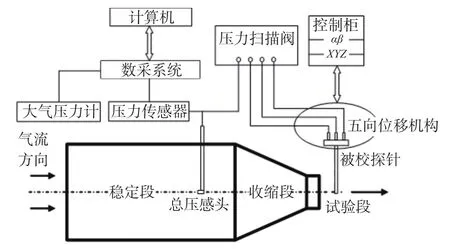
图9 校准系统原理图

3.2 测试方法

1) 对校准实验中用到的压力传感器进行现场检查；

2) 将被校支板后气流角受感部固定在位移机构上，将测量孔对准风洞试验段出口中心，测量孔到风洞试验段出口的安装距离为20 mm；

3) 连接各个压力接头至相应的压力传感器，确保沿程无漏气；

4) 按照校准系统原理图连接校准试验系统；

使用SPSS 17.0软件，利用卡方检验法对2个班的总评成绩以及期末考试试题中每种题型的得分情况进行统计学分析．所有统计分析均采用0.05显著性水平．

5) 运行风洞，调整马赫数到预定的工况；保持该工况，按要求寻找气动零点，记录位移机构在气动零点的位置，完成后调整位移机构回到机械零点；

6) 调整风洞到预定工况点，保持气流马赫数；

7) 调整位移机构改变探针方向夹角，在调整角度时，应保证探针头部位置始终位于风洞核心区内；

8) 待探针压力数据稳定后，开始数据采集，记录此时的总温、风洞总压、风洞静压、大气压、被校探针的输出压力于原始数据表格中；

9) 重复程序7)和8)，进行该工况点其他夹角的校准。

3.3 数据处理方法

3.3.1 气流马赫数Ma

式中：p0——稳定段气流总压，Pa；

3.3.2 总压系数K0

其中pb为试验段气流静压，Pa。

3.4 测试工况

本文为验证数值仿真的准确性，选择方案1中球窝标准结构探针加工成实验件如图10所示，在与2.4节case1工况相同的条件下进行不同敏感角度（–15°、–10°、0°、10°、15°）测试。

图10 压力探针结构试验件

4 结果分析

4.1 网格无关性验证

为验证数值仿真网格无关性，本文通过对球窝型标准结构气流偏转角为0°、15°两种流域分别划分200万、400万、600万、800万网格数量进行仿真。

如图11所示，可以看出在球窝型标准结构气流偏转角为0°时，测压偏差随网格数量的增大而变化较小，其相对变化范围在1%以内，因此，该仿真条件下，200万网格模型即可达到仿真结果与网格数量无关；而在球窝型标准结构气流偏转角为15°时，随着网格数量的增大，测压偏差逐渐减小，且在网格量600万后，测压偏差的变化范围保持在1%以内。因此，本文采用600万网格探针模型网格划分及加密方法对其余探针模型的不同工况进行网格划分及数值仿真即可实现仿真结果与网格数量无关。

图11 不同气流偏转角下网格数量对测压偏差影响

4.2 仿真结果验证

为验证数值仿真方法的准确性，本文对试验件测试结果与600万网格量模型同工况下仿真结果进行对比。如表1所示，总压为114 398 Pa，来流马赫数0.42情况下，气流偏转角从–15°到15°测试结果。可以看出，在总压及马赫数不变的情况下，随着气流偏转角绝对值的增大，测点压差也随之增大，流速随之减小，这一规律符合可压缩气体动量方程；且随着气流偏转角的增大，其总压系数随之增大，尤其在气流偏转角大于10°时，气流偏转角±15°总压系数约为气流偏转角±10°的3倍，且其值远大于0.1%。同时，由于试验过程安装误差等原因，导致相同气流偏转角不同偏向的情况下总压系数不同，负向偏转角总压系数大于相同角度正向偏转角的值，且随着偏转角度越大，不同转向之间的误差越大。

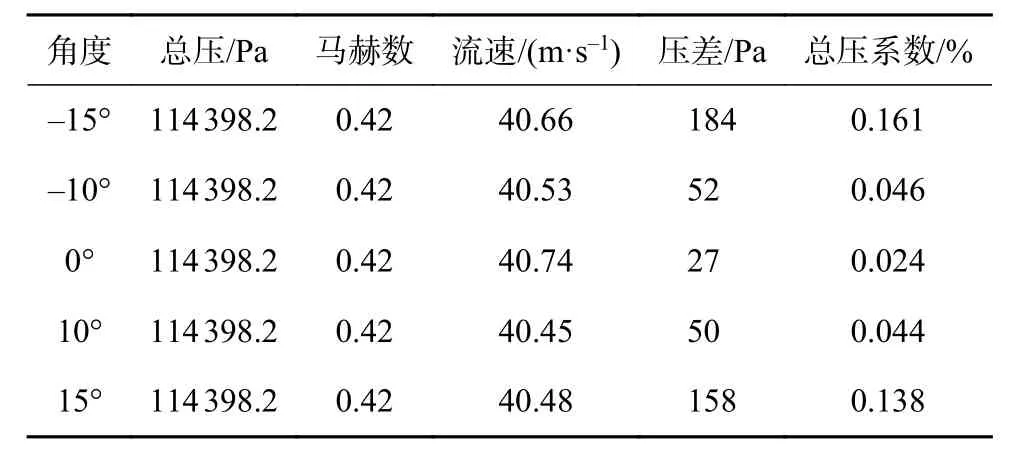
表1 不同气流偏转角下测试结果

因此，本文在验证数值仿真结果时为消除这种实验误差，对正向偏转角与负向偏转角取平均值与仿真结果对比，如图12所示。可以求得，在气流偏转角为0°时，数值仿真结果与试验结果相对误差为3.70%；在气流偏转角为15°时，数值仿真结果与试验结果相对误差为4.91%。综上，数值仿真结果与试验结果相对误差小于5%，表明数值仿真所采用的计算方法正确可信。

图12 不同偏转角下总压系数测试值与仿真对比

4.3 不同结构数值仿真结果分析

对球窝型偏心小内径结构总压探针进行数值计算，分别给出纵向截面的总压云图、静压云图，横向截面的速度云图，球窝附近的速度矢量图，如图13～图16所示。

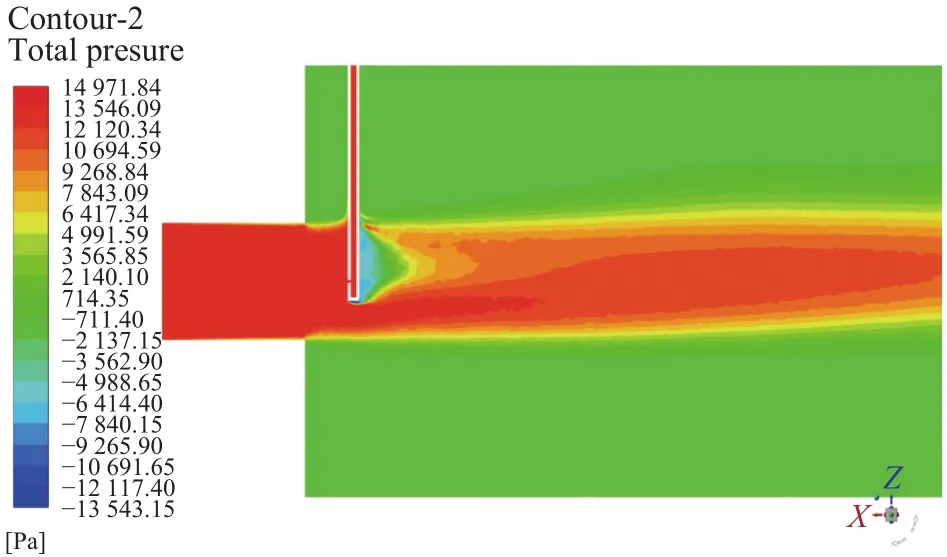
图13 纵向截面总压云图

图14 纵向截面静压云图

图15 横向截面速度云图

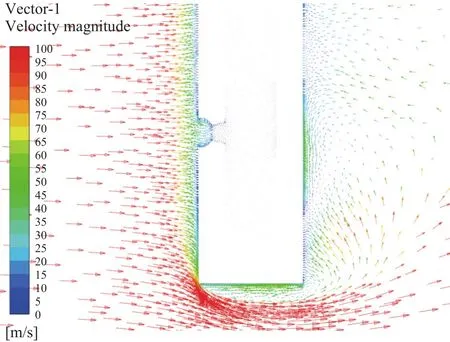
图16 纵向截面速度矢量图

由图13、14、15可知，在总压探针支杆正对来流部分，由于气流受到滞止作用，使得支杆前面正对来流处速度降至约0，根据总压定义，可以认为此处压力升高至接近来流总压；在圆柱支杆的过渡区，气流速度增大压力降低；在圆柱支杆后方，由于气流受到支杆的阻挡产生絮流区，速度再次降低，压力随之升高；由于圆柱支杆的对称结构，使得流场静压在压力探针两侧对称分布。

由图16可知，由于总压探针球面的收缩，对进入到圆柱支杆内的气流产生滞止作用，使得气流流经球窝面后速度快速降低；同时，由于球面的曲面作用，气流在球窝面后形成一个涡，其中，涡内速度在5.0 m/s左右；涡后杆内速度再次减小，低于3.0 m/s。

在相同计算边界条件下，对不同结构的总压探针在气流偏转角15°情况下进行数值模拟计算，其仿真结果如图17、图18及表2所示。其中，图17为五种不同结构总压探针中截面速度云图，由图可知，不同方案总压探针流场内的速度差异较为明显。图18为五种不同结构总压探针球窝内部平均速度，结合图18和表2，方案2与方案1数据对比可知，球窝型偏心小内径结构相比标准结构，球窝内速度明显减小，且其总压系数亦明显减小，表明偏心小内径结构能够有效减小气流在球窝内的压力损失，从而减小总压系数。方案3与方案1数据对比可知，球窝型两侧削平结构相比标准结构，其总压系数减少幅度约为10%，主要是由于球窝两侧削平虽减小气流流经圆柱杆两侧的耗散损失，表明该损失不是影响总压系数的主要因素。方案4与方案5数据对比可知，直孔型压力探针总压系数受直孔孔径的影响非常大，且随着孔径的增大，总压系数减小，在孔径为4 mm时，其总压系数为0.079%。

图17 气流偏转角为15°时不同结构总压探针的速度云图

图18 气流偏转角为15°时不同结构总压探针球窝内平均速度对比图

表2 不同气流偏转角下测试结果

综上分析，球窝内平均速度可用来表征球窝型压力探针总压系数特性，且球窝内平均速度越小，球窝型压力探针总压系数越低，其总压测量恢复特性越好。因此，本文中方案2球窝型偏心小内径结构在气流偏转角15°下其总压恢复特性最佳，且满足工程应用中总压系数小于0.1%的标准。

5 结束语

本文首先根据典型的总压探针设计方法，设计出五种结构形式的总压探针，并在亚声速、常温、常压条件下对这五种典型的总压探针进行数值仿真，通过仿真得到的压力分布、速度分布等流场特性分析总压探针的测压特性，选出不敏感角及测压准确度最优的总压探针进行后续加工，进行实验验证。通过对球窝型标准结构、球窝型偏心小内径结构、直孔型孔径3 mm结构、直孔型孔径4 mm结构、球窝型两侧削平结构五种不同的总压探针在相同亚音速条件下进行数值模拟，分析其各自的流场特性，并计算出总压系数。计算结果表明，气流偏转角对总压的测量结果是有影响的，相对于正吹而言，有偏转角的测点总压偏低，总压系数也相对大些，这与理论分析结果相同。经比较，气流角度对球窝型偏心小内径结构的影响相对较小，其他结构依次是直孔型孔径4 mm结构球、球窝型两侧削平结构、球窝型标准结构、直孔型孔径3 mm结构。因此，球窝型偏心小内径结构的压力探针受气流偏转角度的影响相对较小，测压准确度较高，可以作为现场测试的最佳结构方案。