基于ABAQUS的两弯两矫拉矫机对超高强钢延伸率的影响研究

2022-06-09李碧玲李新龙韩志勇

冶金设备 2022年2期

李碧玲李新龙韩志勇

（1：中冶京诚工程技术公司北京 100176；2：北京科技大学机械工程学院北京 100083）

1 前言

目前，钢铁仍然是汽车车体的主体材料，也是性价比最高的材料。据国际上对汽车用钢的研究［1-3］，用在汽车上的高强钢（High Strength Steel，HSS）是指抗拉强度在270MPa～780MPa之间，而其抗拉强度在780MPa以上的钢称为超高强钢（Ultra High Strength Steel，UHSS）。超高强钢作为一种优秀的车用轻量化材料，其发展和应用为节能减排提供了重要途径。

常见板形缺陷一般是断续出现的单、双边浪（中浪相对少见）、弓背等，且缺陷严重程度不一，复杂多变。高强钢尤其超高强钢变形抗力高，其浪形缺陷的矫平是当前板带钢生产企业的一个重要技术难题［4-6］。

国外关于拉矫机研究最具代表性的是英国学者MORRIS等［7，8］，他们针对模拟拉伸弯曲矫直装置，进行试验研究和相应基于ABAQUS有限元的仿真，针对“一弯”式拉矫过程，在建模过程中考虑了Bauschinger效应（包辛格效应），并对比各向同性硬化和随动硬化准则，发现采用随动硬化准则模型的计算结果更接近试验结果；随后又针对“一弯”式拉矫过程，计算拉矫后带材残余应力，发现带材中部残余应力分布比较均匀而边部分布较为复杂；在此基础上再次模拟试验研究了在“多弯”式拉矫过程中带钢屈服极限和弯曲辊包角等因素对带钢板形的影响，并根据试验数据统计回归建立了数学关系式［9］。但是上述研究只在于拉矫机理的认识和分析，不够全面也无法指导实际工业生产。

当前行业内应用的拉伸弯曲矫直设备主要有两弯一矫与两弯两矫两种辊系布置方式，均包含弯曲单元和矫直单元。两弯两矫拉矫机具有矫直范围大、精度高、速度快、使用灵活等优点被越来越广泛的应用在实际生产中，但相关的理论研究分析相对较少。入口张力及各单元辊系的插入深度对拉矫机弯曲矫直过程中带钢延伸率的影响具有重要的研究意义，对实际生产过程中工艺参数的设定具有重要的指导意义。本文利用有限元ABAQUS软件建立拉伸弯曲矫直过程的有限元仿真计算模型，对两弯两矫拉矫机组的入口张力及各工作辊系插入深度的设定进行研究，分析总结张力大小及插入深度对超薄带高强带钢纵向延伸率影响的规律特点。

2 二维有限元仿真模型的建立

2.1 模型的简化与假设

首先对两弯两矫设备进行研究分析，即两个弯曲单元和两个矫直单元结构，研究其在矫直过程中的应力应变变化历程，通过抽象简化和假设拉伸弯曲矫直过程的力学模型，将前后张力辊及支撑辊等进行简化处理，在模型建立过程中的张力均布施加在带钢头部和尾部的端面处，将实际工作中工作辊的复杂移动简化为模型中参考点的位移载荷约束，在此基础上采用有限元ABAQUS建立拉伸弯曲矫直过程的有限元仿真计算模型。分析超高强钢在弯曲矫直过程中经各工作单元前后的张力变化过程。其两弯两矫辊系布置简化图如图1所示。

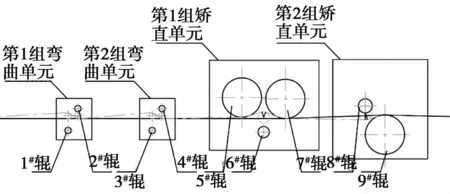
图1 两弯两矫辊系布置简化图

图1中两弯两矫结构从左向右依次为弯曲单元、弯曲单元、矫直单元、矫直单元，从左到右对各工作辊进行标号为1＃，2＃…9＃，其中2对弯曲辊（1＃—4＃辊），辊径大小均为45mm，2＃与4＃辊简化为与带钢上表面相切，5＃和7＃工作辊辊径大小为280mm，7＃工作辊与带钢上表面相切，6＃工作辊辊径大小为60mm，8＃工作辊辊径大小为80mm，9＃工作辊辊径大小为280mm。

对两弯两矫二维有限元模型进行如下简化处理：

（1）各工作辊均为理想圆柱体，不考虑工作辊的磨损及加工误差，忽略工作辊的圆角等特征，工作辊无弯曲变形，考虑到工作辊较带钢变形较小，各工作辊均设置为刚性辊；

（2）研究的带钢力学性能沿板宽方向及板厚方向力学性能一致，及每一横向截面和纵向截面的力学性能及材料的应力应变关系一致；

（3）忽略在带钢发生弹塑性变形过程中由于正向加载引起的塑性应变强化导致带钢在随后反向载荷出现屈服极限降低的现象，即忽略包辛格效应。

（4）假定研究段带钢无初始缺陷，包括板形缺陷和内应力缺陷影响。

2.2 模型的建立

利用ABAQUS有限元软件建立两弯两矫二维有限元模型，模型的建立过程主要包括部件及属性设置、分析步设置、相互作用及载荷设置、网格划分、模型优化等过程，以下介绍模型的建立过程。

（1）几何模型

其两弯两矫二维有限元仿真几何模型如图1所示，带钢运行方向从左向右。在实际拉矫设备工作过程可以近似看作是一个无线连续工作的过程，但在有限元仿真模拟弯曲矫直过程时只能选取其中的一段进行研究，其中带钢总体长度为6400mm，对比弯曲矫直前后研究段带钢长度选取中部处的400mm，各工作辊辊系布置在长度方向的跨度为2500mm，在二维模型中带钢沿运行方向移动3200mm，方可得到完全经过两弯两矫矫直设备后的研究段带钢的矫后应力应变状态。考虑到模拟带钢在穿带时的咬入过程难度较大且实际工作过程为连续弯曲矫直过程，故初始时设置带钢头部长度为3000mm区域内与各工作辊相切，即带钢的上下表面分别与各工作辊相切，便于带钢拖动。

（2）部件及属性设置

定义部件各弯曲辊和矫直辊等为可变形实体单元，在相互作用中约束为刚体，将工作辊简化为圆环形状，如图2所示，相比较设置为解析刚体或离散刚体的优点在于能够更好的模拟工作辊与带钢的接触问题。定义部件带钢为可变形体，带钢的厚度规格为0.7mm、1.2mm，屈服强度700MPa～1500MPa，带钢弹性模量E为210GPa，泊松比μ为0.3。

图2 矫直单元局部放大图

（3）分析步设置

分析步类型设置为静力通用，有限元仿真模型分为6个步骤：

分析步1：本分析步主要是对带钢施加入口张力，设置带钢头部沿X方向移动自由度的约束，在带钢尾部施加特定值的均布张应力载荷，选择载荷中的压强，单位为MPa，张力可由张应力与截面面积相乘得到，分析步时间长度设置为1。

分析步2：本分析步主要是对各工作辊设定初始插入深度为0.01mm以确保与带钢建立稳定的接触，分析步时间长度设置为1。

分析步3：增大各工作辊的插入深度以达到设定值，分析步时间长度为1。

分析步4：设置带钢头部沿运行方向的速度约束，速度大小为1000mm／s，分析步时间长度设为3.2，带钢沿拉矫方向运动3200mm，运行过程中各工作辊为从动辊。

分析步5：采用生死单元方法使研究段带钢的带头与带尾分别与带钢整体分离，在此分析步中将施加在整体带钢尾部的张力设置为未激活状态，将研究段带钢尾部Y方向移动自由度约束，X方向设置一极小速度0.001mm／s保持带钢非常缓慢的运动视为静止，此时带钢内应力释放重新达到新的平衡点。

分析步6：此分析步的作用主要是将分离后的研究段带钢得到充分的变形，以得到完全稳定后的矫直后带钢的应力应变状态。

（4）相互作用及载荷设置

两弯两矫二维有限元模型的相互作用设置主要包括工作辊系与待矫直带钢的接触作用及生死单元法的设置，在模型中设置各工作辊分别与带钢的上下表面接触属性为表面与表面接触，主表面为工作辊外侧表面，从表面分别为带钢的上下面，接触作用属性法向行为“硬”接触，考虑到各工作辊为从动辊，故设置切向行为无摩擦。生死单元的设置建立在分析步5中，选择研究段带钢的头部和尾部的区域如图3所示。

图3 生死单元设置区域

（5）网格划分

网格划分设置沿板厚方向划分为6层（选定某一工况，在厚度方向上划分不同层次网格，计算结果显示表面厚度方向划分6层以上网格结果趋于稳定，考虑计算效率问题厚度方向选定为6层）。沿板长方向设置单元尺寸为5，单元总数为5124，单元形状为线性四边形为主，选择自由网格划分技术，设置进阶算法即在合适的地方使用映射网格，单元类型选择四结点双线性平面应力四边形单元（CPS4R），属性为减缩积分沙漏控制。

3 入口张力和插入深度对延伸率的影响

3.1 入口张力对拉矫过程中的延伸率的影响

在拉伸弯曲矫直设备工作过程中，张力既是力能参数，又是工艺参数，在工作过程中调节前后拉力辊速度差的直接效果就是拉力变化，其间接效是延伸率的变化，因此张力是对拉矫机弯曲矫直过程中塑性变形及矫直质量的重要影响工艺参数。

因研究对象主要为超高强钢，在研究张力的影响规律时，选择带钢规格为屈服强度为1200MPa，厚度取值为0.7mm和1.2mm，板宽为1560mm，各工作辊的插入深度分别为42mm，42mm，48mm，-10mm，21mm（插入深度给定值是以各工作辊分别与带钢上下表面相切时为基准，其中42mm为1＃与3＃辊在带钢发生弯曲变形时向上插入深度，48mm为6＃辊在设备工作时向上插入深度，-10mm为7＃辊在设备工作时向下插入深度为10mm；21mm为9＃辊在矫直设备工作时向上插入深度）。研究弯曲矫直过程中张力在10t～70t时带钢塑性延伸应变及残余应力的影响规律，设置入口张力为10t，20t，30t，40t，50t，60t，70t，在板厚为1.2mm 时分别对应的应力为53.42MPa，106.84MPa，160.26MPa，213.68MPa，267.09MPa，320.51MPa，373.93MPa。之后在此应力基础上计算厚度为0.7mm 下的应力应变情况。

在有限元模拟结果中可以得出带钢的相应的出口张力大小，在带钢厚度分别为0.7mm及1.2mm下不同入口张力的计算结果如图4、图5所示。

图中εm表示带钢中心层纵向塑性延伸，εa表示带钢平均塑性延伸应变，εmax表示带钢纵向最大塑性延伸应变。

由图4及图5结果所示，板厚为0.7mm时，当入口张力低于213.64MPa时，带钢中心层纵向塑性延伸应变为0，当入口张力在213.64MPa～373.87MPa时，带钢纵向塑性延伸应变逐渐增加；板厚为1.2mm时，当入口张力在低于160.23MPa时，带钢中心层塑性延伸应变为0，当入口张力在160.23MPa～373.87MPa范围时，带钢中心层纵向塑性延伸应变逐渐增加。

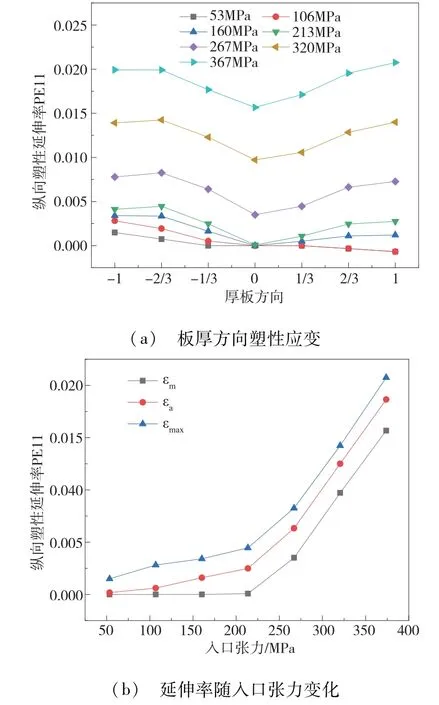
图4 板厚为0.7mm时带钢矫后塑性变形规律

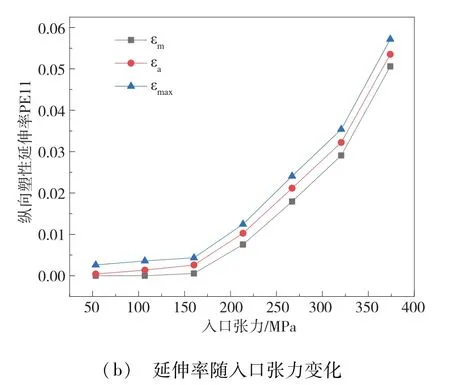
图5 板厚为1.2mm时带钢矫后塑性变形规律

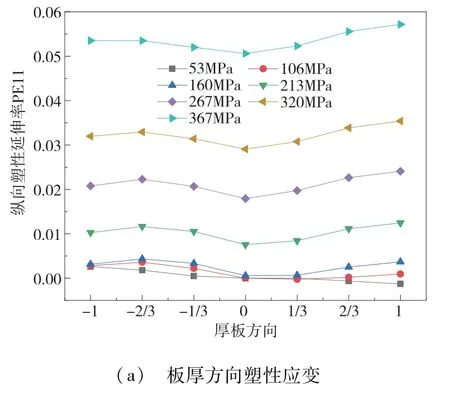
可以得出结论，随着入口张力的增大，带钢纵向塑性延伸是增大的，但是其影响规律并非是线性变化的，存在最小张力的阈值，即当张力小到一定程度，带钢中性层不会发生塑性变形，而当张力大于此阈值时，最终张力的增大其纵向塑性延伸显著增大。

3.2 插入深度对拉矫过程中的延伸率的影响

插入深度是对拉矫机弯曲矫直过程中塑性变形及矫直质量的重要影响工艺参数，弯曲单元的主要作用是消除和改善初始板形缺陷，矫直单元主要是改善由于初始及弯曲单元产生的横向与纵向翘曲，因此分析各弯曲单元和矫直单元中分别给定不同的压下量产生的影响具有重要的意义，研究在带钢弯曲矫直过程中带钢的应力应变状态，对实际带钢板形拉矫过程插入深度的设定提供一定的理论指导。

以屈服强度1200MPa，厚度为1.2mm的带钢为研究对象，张力为213.64MPa，研究15种不同压下方式对应力应变的影响规律总结，主要分为三组，其中第一组的方式1-5的d1，d2，d3参数设置相同，仅改变参数d4，d5，研究插入深度d4，d5对矫后带钢延伸率分布的影响；第二组和第三组设置d1，d2，d3，d4相同，研究d5对矫后带钢的影响。不同组别之间可以对比d1，d2，d3带来的影响，其插入深度计算工况如表1所示。

表1 插入深度工况设定表

针对屈服强度为1200MPa，厚度为1.2mm规格的带钢，其不同插入方式的计算结果如图6、图7及图8所示，其中C1层为带钢上表面，C7层为带钢下表面，依次均布划分为C2至C7层。

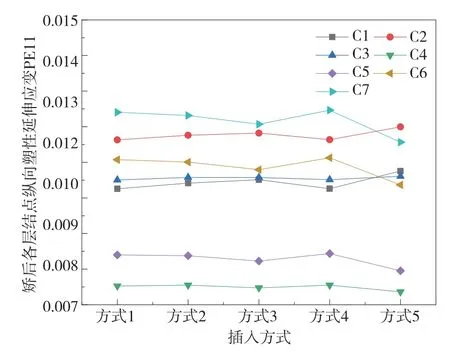
图6 方式1-5矫后板厚方向塑性变形规律

图7 方式6-10矫后板厚方向塑性变形规律

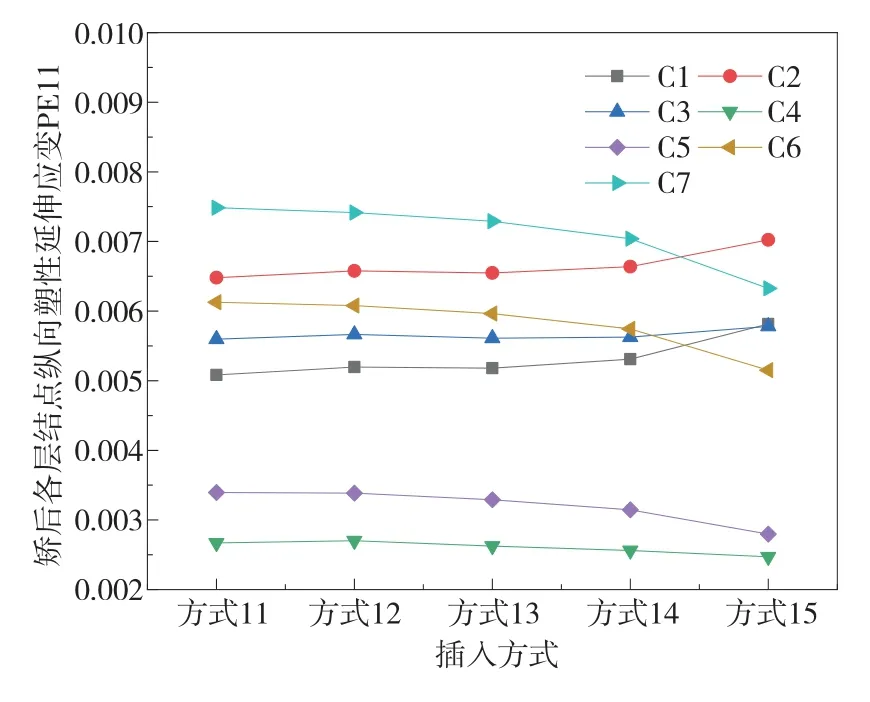
图8 方式11-15矫后板厚方向塑性变形规律

根据图6结果可得，整体来看压下方式1到方式5各层结点纵向塑性延伸应变波动不大，其中中心层纵向塑性延伸应变最小，其余各层的纵向延伸率大小较中心层大，C7层的纵向塑性延伸应变最大为0.0123，C2层的纵向塑性延伸应变次之为0.0117，此后依次为C6、C3、C1、C5层，中心层纵向塑性延伸应变最小为0.0075，可以看出在高强钢弯曲矫直过程中带钢沿板厚方向的纵向延伸分布并非由中心层向带钢上下表面逐渐增大，其原因为带钢在经过拉伸弯曲矫直过程由于受到弯曲辊组和矫直辊组的共同作用。对比方式1、方式2和方式3可得，在d1，d2，d3，d4保持不变的插入深度，改变d5的插入深度由方式1的21mm到方式2的20.5mm再到方式3的20mm，可以发现带钢沿厚度方向各层结点的纵向塑性延伸应变变化不大，故单独调节d5对带钢板厚方向的各层单元结点的纵向塑性延伸应变影响不大；由方式4和方式5对比可得，调节d4和d5的值，由图可知各层结点纵向塑性延伸应变出现波动，并且厚度方向的纵向延伸应变大小发生改变，塑性应变值由大到小依次为C2，C4，C1，C3，C6，C5，C7。

由图6、图7及图8结果对比显示，可以看出方式6-10、方式11-15在弯曲矫直过程中厚度方向各层单元结点纵向塑性应变及纵向残余应力变化趋势及规律与方式1-5近似，在此不在赘述，但值得注意的是，以带钢中心层的纵向塑性延伸εm为指标，可以发现方式1-5带钢中心层纵向塑性延伸应变约为0.0075；方式6-10带钢中心层纵向塑性延伸应变约为0.0051；方式11-15带钢中心层纵向塑性延伸应变约为0.0026；由此可以得出改变插入深度d1、d2、d3，对带钢在拉矫过程中纵向塑性延伸应变影响较大。