拉盖尔-高斯光束入射石英基底石墨烯涂层的透射光强分布特性研究

张艺伟,王明军,王 姣

(1.西安理工大学自动化与信息工程学院,陕西 西安 710048;2.陕西科技大学电子信息与人工智能学院,陕西 西安 710021)

1 引 言

在近几十年来,拉盖尔-高斯光束是目前研究较多的涡旋光束之一,因其具有的许多光学特性。使其在光学微操控[1]、光信息传输[2-4]、驱动微粒旋转成像[5]、激光光学[6]、雷达目标探测[7-9]等领域的应用得到了广泛的研究。而其中涡旋光束在不同介质中传输特性的研究也成为了当下该光束研究的一大聚焦点。目前,多研究涡旋光束在介质传播过程中的反射光强和透射光强的场分布特性,例如:将涡旋光束通过石英基底来进行实验研究其光强分布变化。在实际应用中,把其光场强度的分布在一定程度上进行改变,来得到有不同外形的光强分布[10]。

石墨烯材料是由碳原子构成的新型二维平面薄膜材料[11]。其碳骨架周围分布着丰富的点资源,导致电子之间容易形成π-π堆叠,形成多层的石墨结构,而且其具有相对较强的光吸收特性,这些独特的光学特性使得石墨烯材料在光学领域具有广泛的应用前景[12-13]。

目前,国内外学者对于涡旋光束经过不同介质后的传输过程中,对其光强分布特性进行了深入研究。Salla等[14]将涡旋光束通过做实验进行研究得到了改变拓扑荷数后散斑的变化。李新忠等[15]对涡旋光束照射毛玻璃之后的光场进行了研究。关于石墨烯材料的研究发现,石墨烯材料的非线性响应与其层数和石墨烯薄膜厚度相关,Hendry[16]已证实在石墨烯层数小于6时,其非线性系数随层数和厚度呈线性增加趋势。潘登科等人[17]研究了石墨烯的透射系数与化学势之间的关系。石墨烯在光学领域中的特性使研究学者们对其进行研究,从上述研究概况可以看出目前关于石墨烯在光学领域基本上讨论的都是平面波入射情况,关于拉盖尔-高斯涡旋光束入射石墨烯涂层的界面情况较少报道。

本文利用角谱衍射理论和数字滤波技术,将石墨烯涂层覆盖于石英基底上模拟为一组双层粗糙面进行仿真,研究分析了拉盖尔-高斯光束通过该模型的透射光强分布特性,通过改变石英基底的方向自相关长度,石墨烯涂层的厚度,拉盖尔-高斯光束的拓扑荷数这三种参数,详细讨论了其对光强分布特性的影响,并进行了实验验证。研究结果对于激光入射多层膜结构器件的应用具有一定的意义。

2 拉盖尔-高斯光束通过石英基底石墨烯涂层的双层模型的理论基础

建立物理模型如图1所示,拉盖尔-高斯光束垂直入射双层石英基底石墨烯涂层粗糙面上。

图1 拉盖尔-高斯光束通过双层石英基底石墨烯涂层Fig.1 The Laguerre-Gaussian beam passes through a graphene coating on a two-layer quartz substrate

使拉盖尔-高斯光束沿z轴传输,当z取0时,其光场强度为[18]:

(1)

通过粗糙表面后的光场为[19]

Enh(r,φ)=E(r,φ)exp[-ik(n-1)h(r,φ)]

(2)

式中,k为波数;n为粗糙表面的折射率;h(x,y)为粗糙表面的高度分布函数。通过粗糙表面后的光场可由角谱衍射理论表示为[20]:

(3)

式中,fx,fy为空间频率;F-1{·}为傅里叶逆变换;F{·}为傅里叶变换。由式(2)可知,得到通过粗糙表面后的光场,需要得到粗糙表面的高度分布函数。本文通过数字滤波技术,模拟出高斯分布条件下粗糙表面的自相关函数,其自相关函数为以下形式:

(4)

式中,σ为表面均方根高度;βx为x方向上的相关长度;βy为y方向上的相关长度,因为石墨烯材料为各向异性,当介质表面特性为各向异性时,相关长度取βx≠βy。滤波器的传递函数H(wx,wy)为:

(5)

式中,C为功率谱密度;Gz(wx,wy)为功率谱密度函数。其高度分布函数为:

h(x,y)=F-1{Z(wx,wy)}

=F-1{H(wx,wy)A(wx,wy)}

(6)

(7)

式中,e是电子量；ħ是约化普朗克常数；τ=0.1 ps是弛豫时间；w=2f是角频率；T是温度；μc是石墨烯的化学势；KB是玻尔兹曼常数。根据石墨烯的电导率可等效出石墨烯层的折射率[22],即:

(8)

式中,εg为石墨烯层的相对介电常数;Δ为单层石墨烯的厚度;ε0为真空介电常数。可通过石墨烯电导率来表示其相对透过率,由菲涅尔定理[23]得到为:

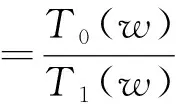
(9)

拉盖尔-高斯光束透过石墨烯表面的透射光场公式为:

E2=E(r,φ,z)τg

(10)

先将拉盖尔-高斯光束通过单层石墨烯粗糙面的光场E1利用式(3)推导得到,当E1经过石墨烯厚度后透过光场为E2由式(10)推导得到,最后通过将E2代入式(3)得到再次入射石英基底粗糙面的光场为E3,E3为拉盖尔-高斯光束通过所建立模型传输的透射光场。

3 仿真与实验结果分析

3.1 石英基底对拉盖尔-高斯光束光强的影响

模拟拉盖尔-高斯光束原始光强,光束的拓扑荷数l=1、波长为λ=632.8nm、径向粒子数为0,束腰半径w=2mm。如图2所示:

图2 拉盖尔-高斯光束光强图Fig.2 Laguerre-Gaussian beam intensity diagram

取不同方向相关长度βx=0.02 mm,βy=0.02 mm、均方根高度为σ=0.01 mm数值模拟高斯粗糙面,如图3所示。

图3 高斯粗糙面Fig.3 Gaussian rough surface

将上述图2模拟仿真的拉盖尔-高斯光束入射到图3所示的石英粗糙表面上,得到拉盖尔-高斯光束通过粗糙表面后的光强分布图4。由图4可以看出,拉盖尔-高斯光束透过粗糙表面的光强强度减弱。当光束光强经过粗糙面后,受粗糙面的影响光斑变得不再光滑,在光束光斑上出现了黑色斑点,将该仿真现象在本文中称为暗斑。

图4 拉盖尔-高斯光束通过石英粗糙表面的光强分布Fig.4 Intensity distribution of a Laguerre-Gaussian beam passing through a random rough surface

3.2 单层石墨烯涂层对拉盖尔-高斯光束光强的影响

对拉盖尔-高斯光束垂直入射单层石墨烯粗糙面的模型进行了数值模拟。令入射光束的波长为λ=632.8 nm、束腰半径w=2 mm、径向粒子数为0、表面均方根高度σ=0.01 mm、传输距离为200 mm的值一定。取方向相关长度βx=0.01 mm,βy=0.02 mm值一定。如图5所示,(b)、(f)取厚度Δ=1 nm,(c)、(g)取厚度Δ=5 nm,(d)、(h)取厚度Δ=20 nm。(a)～(d)为拓扑荷数l=1,(e)～(h)为拓扑荷数l=3。

图5 不同拓扑荷数下,拉盖尔-高斯光束通过不同厚度单层石墨烯粗糙表面的光强分布Fig.5 The intensity distribution of Laguerre-Gaussian beam passing through the rough surface of graphene monolayer with different thickness under different topological charge numbers

在图5中光束光斑始终保持圆环状,中心强度为0,当涡旋光束通过单层石墨烯粗糙面时,改变拓扑荷数,仅对拉盖尔-高斯光束光斑的尺寸大小有影响,拓扑荷数和光斑尺寸成正比；改变石墨烯的厚度,拉盖尔-高斯光束透过石墨烯表面后的光强强度随着石墨烯厚度的增加而减弱,石墨烯的厚度与光强强度成反比。

3.3 石英基底石墨烯涂层的双层结构对拉盖尔-高斯光束光强的影响

如图6所示,双层石墨烯涂层石英基底粗糙面,石英的厚度为2 mm,设置石墨烯薄膜的厚度为Δ=20 nm和方向相关长度βx=0.01 mm,βy=0.02 mm的值不变,(a)～(c)为拓扑荷数l=1,(d)～(f)为拓扑荷数l=3,(b)、(e)为通过单层石墨烯表面后的光强,(c)、(f)为通过双层石墨烯涂层石英基底粗糙面的光强。对比了通过单层石墨烯和双层石墨烯涂层石英基底粗糙面时,光束的光强分布变化。

图6 不同拓扑荷数下,拉盖尔-高斯光束通过不同厚度双层石墨烯粗糙表面的光强分布Fig.6 Intensity distribution of Laguerre-Gaussian beams passing through rough surfaces of layered graphene with different thickness under different topological charge numbers

图6中改变拓扑荷数,其对拉盖尔-高斯光束的影响与通过单层石墨烯的光斑变化相同,均对光束空心分布影响微弱,增加一层石英介质相较于单层石墨烯粗糙面,透射光束强度大幅度减弱,可以看出光强分布强度等变化主要由不同介质或介质的不同厚度所影响。

图7中取石墨烯涂层的厚度Δ=20 nm,因石墨烯材料特殊的各向异性,所以取βx≠βy,(a)～(c)为拓扑荷数l=1,(d)～(f)为拓扑荷数l=3。(b)、(e)为不同方βx=0.02 mm、βy=0.06 mm时光强分布。(c)、(f)为不同方向相关长度βx=0.03 mm、βy=0.09 mm时光强分布。

图7 不同拓扑荷数下,拉盖尔-高斯光束通过不同相关长度双层石墨烯粗糙表面的光强分布Fig.7 Intensity distribution of Laguerre-Gaussian beams passing through the rough surfaces of double-layer graphene with different correlation lengths under different topological charge numbers

图7中改变拓扑荷数,其对拉盖尔-高斯光束的影响与通过单层石墨烯的光斑变化相同,当光束通过单层石墨烯时,取不同的方向相关长度,拉盖尔-高斯光束透过石墨烯粗糙面后的光强随着相关长度取值增大而减弱,光强与方向相关长度成反比。受粗糙面影响变大,光强分布中暗斑明显变大变多。当光束通过双层石墨烯涂层石英基底时,光束透过粗糙表面的光强相比于单层石墨烯粗糙面明显减弱,光斑受粗糙面影响对比于单层石墨烯薄膜变化明显。

3.4 拉盖尔-高斯光束通过石英基底石墨烯涂层双层结构的实验研究

本文为研究拉盖尔-高斯光束光束透过基于石英基底石墨烯涂层双层结构的光学特性,设计了一组实验进行验证,其实验原理图如图8所示。

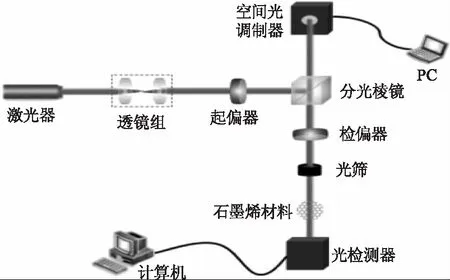
图8 实验原理图Fig.8 Experimental schematic diagram

本文运用控制变量法,在实验中只改变拉盖尔-高斯光束透过不同厚度的石墨烯涂层,实验所采用的设备有:石墨烯材料激光装置,包括基台,基台上固接有发射链路和检测链路,发射链路和检测链路呈垂直直角关系,检测链路包括石墨烯材料,发射链路通过发射信号给检测链路,检测链路完成对石墨烯材料的检测。

实验中使用波长为λ=632.8 nm的激光器,透镜焦距f=200 nm。其发射链路包括顺次连接的激光器、第一透镜、第二透镜、起偏器、分光棱镜,检测链路包括顺次连接的终端、光检测器、石墨烯材料、光筛、检偏器、分光棱镜、空间解调器SLM,发射链路和检测链路通过分光棱镜呈直角连接。首先,激光器发射高斯光束到第一透镜和第二透镜,第一透镜和第二透镜透射使得高斯光束准直扩束,然后透过起偏器和分光棱镜发生反射和透射,将反射的光束再一次垂直入射到空间光调制器SLM中,最后得到了拉盖尔-高斯光束。

产生的拉盖尔-高斯光束再透过分光棱镜射出,再经过检偏器和光筛,通过调节光筛来筛选出光强最强、分布最均匀的光束,将其打到每组实验中的石墨烯涂层材料上。

透过石墨烯涂层的光束再入射到光检测器中,再通过终端中的BeamGage软件将信息直接传输出来。其实验现场图和结果如图9和图10所示。

图9 实验现场图Fig.9 Experimental field diagram

图10 涡旋光束光强图Fig.10 Optical intensity diagram of vortex beam

图10(a)为通过一个长宽2.5 cm×2.5 cm,厚2 mm的空白石英基底后的光强图。图10(b)为通过一个长宽2.5 cm×2.5cm,厚2 mm的石英基底涂抹了5 nm厚石墨烯涂层后的光强图。图10(c)为通过一个长宽2.5 cm×2.5 cm,厚2 mm的石英基底涂抹了20 nm厚石墨烯涂层后的光强图。

由图10可以看出,在同一条件下,随着材料厚度改变,其光束的光斑图像明显地看到由亮变暗。经过石英基底的光束的光斑光强最强。经过5 nm厚石墨烯涂层石英基底的光束的光斑光强相较石英基底变暗。经过20 nm厚石墨烯涂层石英基底的光束的光斑光强最弱。当光束光强经过粗糙面后,受粗糙面的影响光斑变得不再光滑,在光束光斑上也出现了黑色斑点。

4 结 论

本文利用角谱衍射理论,研究了拉盖尔-高斯光束通过石英基底石墨烯涂层这组双层结构的透射光强分布特性,仿真计算了拉盖尔-高斯光束经过不同方向自相关长度的石英基底、不同厚度的石墨烯涂层后的光强分布,结果表明:石墨烯涂层的厚度和石英基底的方向自相关长度对拉盖尔-高斯光束的空心分布几乎没有影响；拉盖尔-高斯光束通过石墨烯涂层的光场强度随着石墨烯涂层厚度的增加而逐步变弱,光场强度与厚度成反比,当厚度大于20 nm时,衰减明显变大,石英基底石墨烯涂层这组双层结构对比于单层石墨烯涂层衰减更为显著。当石英基底的方向自相关长度增大时,光场分布受其影响变大,光场中的暗斑明显变大变多。暗斑的变化仅与的方向自相关长度有关。与单层和双层粗糙面模型无关,实验和理论的光强变化一致。本文的研究结果对于石墨烯在光学、光电子领域的应用和发展具有一定的价值。