一种基于激光雷达探测的风场多特征反演方法
2022-06-09张旭晖李健兵
周 洁,高 航,张旭晖,李健兵
(1.国防科技大学电子科学学院,湖南 长沙 410073;2.海军91236部队,辽宁 葫芦岛 125100)
1 引 言
风是日常生活中最常见的一种自然现象,对人类生产生活产生巨大的影响,风中蕴含巨大的破坏能量,一旦感知不当,就将造成严重的人员伤亡和经济损失。2021年3月23日,“长赐号”货轮在苏伊士运河河口南端6海里处疑遭瞬间强风吹袭,造成船身偏离航道,触底搁浅。搁浅事件造成了巨大损失,全球12 %的国际贸易通道被该货轮“切断”,经济损失估计超过数十亿美元。2015年6月1日2130左右,重庆东方轮船公司所属“东方之星”游轮上行至长江水域湖北荆州市监利县大马洲水道44号过河标水域处,遭遇严重垂直切变和水平切变灾害性天气,导致游轮翻沉,442人遇难[1]。2018年8月28日,首都航空JD5759航班在澳门机场着陆时出现“海豚跳”,在双发不同程度受损、前起落架断裂情况下复飞备降深圳,事故原因查明是突遇严重风切变[2]。
在众多灾害性风场气象当中,低空风切变及湍流是国际上公认的严重危害飞行安全的风场现象。低空风切变通常是指近地面600 m高度以下风矢量(风向、风速)在水平和(或)垂直距离上的变化[3];湍流是指风速的时间不规则性和空间的不均匀性由各种尺度的漩涡连续分布叠加形成[4]。目前,用于风切变和湍流探测技术主要包括测风仪、气象雷达、风廓线雷达以及激光雷达,其中激光雷达被认为晴空条件下较优的风场探测系统。
采用激光雷达对风切变和湍流探测的扫描策略有多种,主要包括平面位置显示器(Plan Position Indicator,PPI)、距离高度显示器(Range Height Indicator,RHI)[5]、多普勒波束摆动(Doppler Beam Swinging,DBS)[5]、凝视[6]、滑动路径扫描(Glide Path Scan,GPScan)[7]等方式。常见的扫描方式,只能够实现对于单一高度角或者方位角区域风切变和湍流的探测,且存在空间覆盖范围和数据更新率之间的矛盾,为克服该问题,国内外开展了相关研究。2011年,陈柏纬等人基于下滑道扫描方式,利用F因子实现了对风切变的精准预测,并采用纵向结构函数实现了低空湍流预警算法,其扫描周期比传统的PPI扫描短,从而提高了预警效率[8],但无法同时实现对于机场三维风场的探测。2015年,Sathe在常规5波束DBS扫描方式基础上,通过最小化风场矢量测量随机误差矩阵构建了六波束扫描方式,并在此基础上实现了对风场廓线和湍流参数的快速探测反演[9],但该方法采用固定高度角扫描,无法感知全域三维空间,只能提供风场廓线信息;2008年,Banakh和Smalikho基于RHI扫描方式,采用径向速度谱反演湍流耗散率[10],2019年,采用2高度角PPI扫描方式,实现了对于非均匀湍流特征参数的探测和反演[11],该方法实现了对于各向异性湍流的探测感知,但其空间垂直采样率不足。2017年,Norman等人位于葡萄牙开展湍流观测实验,利用一部采用垂直凝视方式和二部RHI扫描方式的激光雷达,利用修正的多普勒谱宽方法实现了对湍流和风切变以及低空急流的演变过程的探测[12],该实验基于多部激光雷达协同探测,原始数据准确性提升,但经济成本和多雷达协同方式难度增加。
综上所述,现有各种扫描方式只能实现特定的风场特征获取,为同时实现大范围三维风场、湍流强度、风切变的反演,亟需提出一种兼顾空间覆盖范围、时空分辨率及鲁棒性的激光雷达体积扫描方法。本文提出一种晴空条件下的多用途的测风激光雷达体积扫描策略及风场特征获取方法,采用交替多个特定高度角的圆锥扫描方式,基于局部线性风场假设条件,在郎需兴等人二维风场反演方法基础上[13],通过径向风速的处理实现三维风场的反演(后称为3D-VPP方法);通过计算特定高度角下飞机下滑道区域F因子强度,实现对风切变强度的评估和预警[7,14-15];利用35.3°高度角圆锥扫描,采用部分傅里叶分解算法,快速计算湍流动能强度廓线分布情况;应用均匀湍流假设,通过计算径向速度结构函数,建立湍流耗散率与径向速度纵向结构函数关系式,从而计算该区域湍流耗散率分布情况[11]。通过仿真比对实验,验证了本方法对于机场周边风切变和湍流的探测反演具有较好的性能。
2 方法介绍
2.1 体积扫描方式
在晴空条件下,激光雷达通过大气气溶胶粒子后向散射信号的多普勒频移获得扫描空间中风场的径向速度。激光雷达体积扫描示意如图1(a)所示,在多个高度角作PPI(Plan Position Indicator)扫描,该扫描方式可以获得更大的扫描波束覆盖范围,可为精细的风场反演算法提供足够的数据支撑。
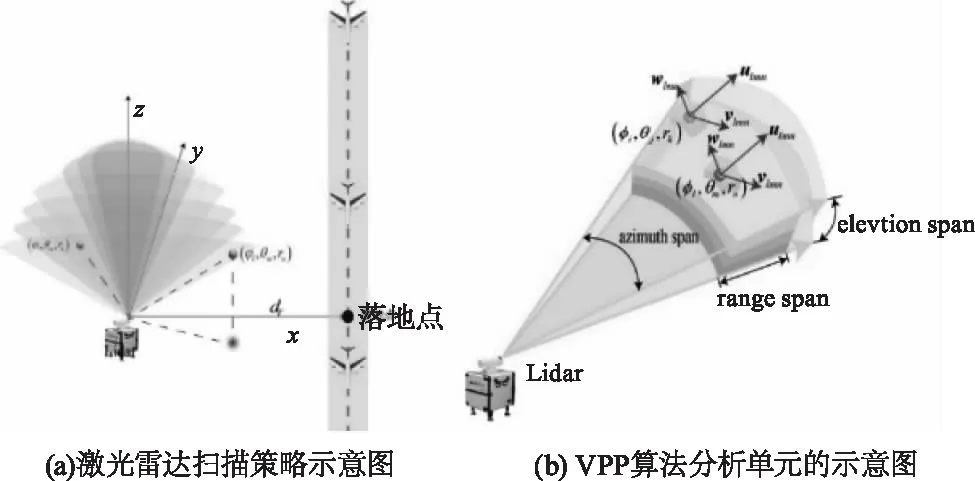
图1 激光雷达扫描策略和VPP算法分析单元的示意图Fig.1 Schematic diagram of lidar scanning strategy and schematic diagram of VPP algorithm
激光雷达应部署在飞机降落点附近,确保激光雷达与飞机下滑道之间无障碍物遮挡,激光雷达有效探测距离Rmax能完全覆盖飞机下滑道所有区域。进行体积扫描时交替采用多个不同高度角PPI扫描的方式,其中包含φ=1°,3°,35.3°,90°这4个特定的高度角,1°高度角主要实现对于近地面风场的探测,3°高度角主要实现对于飞机下滑道区域风切变的探测,35.3°高度角主要实现对于湍流的探测和湍流动能强度的快速计算,90°高度角作为垂直风速参考。其余高度角可按照φ=1°、3°、8°、15°、25°、35.3°、45°、90°进行配置,若特定区域需进行重点扫描,可进行加密配置,但需满足2个相邻高度角之差Δφ<10°,最大高度角根据所测空域高度需求及Rmax而确定(45°满足600 m以下空域探测需求)。激光雷达旋转角速度、扫描扇区大小可根据关注的探测空间区域而调整,在每个高度角采取完整PPI或者扇区PPI扫描方式获得各高度角的径向速度信息。
基于该扫描方式,在保证探测精度的同时,兼顾数据更新率,可以同时实现风场三维速度反演、下滑道的风切变识别、湍流动能强度和耗散率廓线的有效探测。
2.2 风场反演算法
在2.1节提出的体积扫描方式基础上,采用3D-VPP方法实现对于探测空域的三维风场的反演。建立以激光雷达为原点的笛卡尔坐标系(x,y,z)和球坐标系(φ,θ,r),如图1(a)所示,x,y,z分别为垂直机场跑道方向、平行跑道方向和垂直方向上距激光雷达的距离,φ为高度角,θ为方位角,r为到激光雷达的径向距离。在激光雷达扫描空间中,将高度角跨度插值为φi∈[φl-Iδφ,φl+Iδφ],方位角跨度为θj∈[θm-Jδθ,θm+Jδθ],径向距离跨度为rk∈[rn-Kδr,rn+Kδr]的连续区域作为分析体积单元Almn,其中O(φl,θm,rn)是该分析单元的中心,δφ,δθ,δr分别为激光雷达的高度角、方位角和径向距离分辨率,lmn表示扫描空间中的第lmn个探测单元,示意图如图1(b)所示。2I+1,2J+1,2K+1分别为分析体积单元内高度角、方位角和径向分辨单元的个数,φi,θj,rk分别为分析单元内任意一点的高度角、方位角、径向距离。
设分析单元中心点速度为(ulmn,vlmn,wlmn),ulmn表示径向速度,vlmn表示水平切向速度,wlmn表示ulmn,vlmn所在平面法向的垂直速度。对于较小尺度的分析单元,可以认为单元内所有速度相等,则分析单元内任一点P(φi,θj,rk)的径向速度Vobs(φi,θj,rk)与中心点风速在其径向上的风速投影F(φi,θj,rk)可以表示为式(1)。
使分析单元内观测到的径向风场Vobs(φi,θj,rk)与各径向的投影风场F(φi,θj,rk)之间差的平方和最小建立目标函数式。目标函数分别关于vlmn,wlmn作变分处理,并令∂H/∂vlmn=0和∂H/∂wlmn=0,可以得到使H取极小值时的vlmn,wlmn速度的大小,ulmn,vlmn,wlmn的表达式可以表示为式(2),将反演速度转为笛卡尔坐标系中速度(u,v,w)。
F(φi,θj,rk)=ulmn[cosφlcosφicos(θm-θj)+sinφlsinφi]-vlmncosφisin(θm-θj)+
wlmn[cosφlsinφi-sinφlcosφicos(θm-θj)]
(1)
(2)
2.3 下滑道风切变算法
假设飞机下滑道是具有一定尺度的管道区域,以3°飞机下滑道为轴选取附近30 m范围内的风场数据,示意图如图2所示。激光雷达到跑道的距离为dT,着陆点与激光雷达到跑道垂足的距离为dL,激光光束与跑道的夹角为Θ,下滑道上径向数据点到y轴的距离为dH,且dH=(y-dL)tan3°。

图2 飞机下滑道区域的示意图Fig.2 Schematic diagram of the aircraft glide path

2.4 湍流特征参数反演算法
基于均匀湍流假设条件,在湍流惯性副区当中,可以采用统计学方法进行相关湍流特征参数的计算和反演,其中湍流动能强度和湍流耗散率是最主要关注的量。本方法对机场上空完成一次扫描时间仅需几分钟,且PPI扫描水平投影半径满足远大于湍流场外尺度条件,因此认为湍流特征没有发生明显变化,符合静态、均匀条件。
2.4.1 湍流动能强度算法


(3)
其中,〈·〉θ表示按方位角取平均值,使2/tan2φ=1,φ=35.3°,可快速地获取湍流动能强度计算公式(Turbulence Kinetic Energy,TKE):

(4)
2.4.2 湍流耗散率算法

(5)
其中,tδr=R1-R2要满足tδr≤Lv;δr为径向距离间隔;t=0,1,2,…,Lv为湍流外尺度;R1,R2为到激光雷达的径向距离;k=0,1,2,…,K;N为有效速度波动总次数;θm=m·δθ为方位角,δθ为方位角精度,m=0,1,2,…,M;E(R1,R2)为测量误差的无偏估计,本文采用脉动速度差的协方差计算测量误差。
基于Kolmogorov的局地均匀各向同性湍流理论,当径向距离间隔r≪Lv时,其结构函数可以近似表示为[4]:
Dv(r)=Cvε2/3r2/3
(6)
其中,Cv≈2为Kolmogorov常数;ε为湍流耗散率,将计算得到的速度结构函数公式(5)与公式(6)联立,可得到相应的湍流耗散率强度。
3 比对结果和分析
3.1 仿真设置
仿真激光雷达在每个仰角上作完整的PPI扫描,设置扫描仰角为φ=1°、3°、8°、15°、25°、35.3°、45°、90°,在每个仰角上,雷达扫描的方位角范围为θ0+m·δθ,其中θ0=0°,δθ=5°,m=0,…,72,探测单元到激光雷达的径向距离为r0+k·δr,其中r0=0 m,δr=10 m,k=0,…,100,扫描示意图如图1所示。为了充分验证本方法对于在复杂风场探测性能,仿真风场包含均匀项、湍流项及风切变项3部分,具体仿真风场为:
(7)
其中,X,Y,Z∈L×M×N分别为探测单元在以激光雷达为原点的笛卡尔坐标系(如图1所示)中的x,y,z坐标;Uturb是采用伪小波方法[18],给定湍流耗散率为5×10-4m2/s3仿真所得到的湍流速度,如图3(a)所示。Ushear是根据风切变的流体力学特征,结合小尺度气象学通过函数拟合方法[19],给定垂直初始风速为10 m/s强度下所获得的三维低空风切变速度,如图3(b)所示。

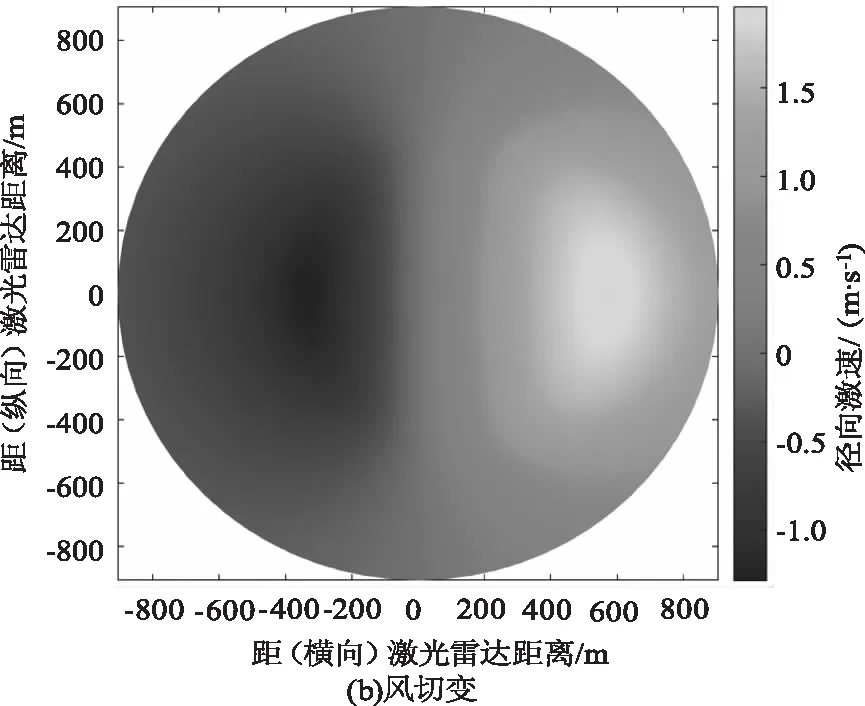
图3 湍流和风切变仿真示意图Fig.3 Simulation of turbulence and wind shear
3.2 仿真结果分析
根据仿真的背景风场,采用本方法分别对反演的三维风场、风切变F因子、湍流动能强度以及湍流耗散率进行计算,并与真值进行了比较。
3.2.1 三维风场反演算法验证
图4给出了采用本方法反演的三维风场与仿真风场的对比情况,使用相关系数和均方根误差用于定量表征风速分量的反演误差。从图4中可以看出,采用3D-VPP方法反演的水平风场与仿真风场吻合度较高,相关系数可达0.9以上。因该方法直接使用径向速度作三角变换计算其他风场分量,因此经反演后合成的径向速度与初始径向速度相同,但使用该方法反演垂直风速时误差较大,修改背景风场中风切变类型为线性风场,其他条件保持不变时,此时各高度角垂直风速之间具有较强相关性,再次使用本方法反演垂直风速时性能较好,均方根误差可控制在0.7 m/s,性能相对于非线性风场具有较大提升。为验证本方法的反演性能,采用VAD方法基于线性风场假设对各高度层二维风速进行反演,并与仿真风速进行比对,图4(c)、(d)所示,VAD方法与3D-VPP方法相比,反演精度较低,相关系数均小于0.7,对于非线性风场反演较差。

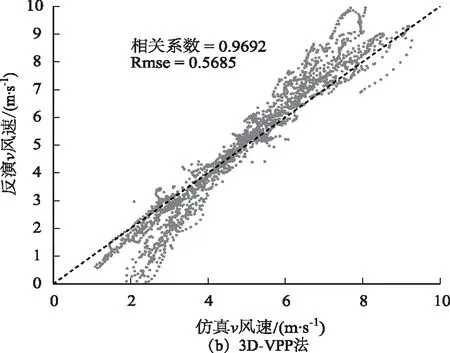

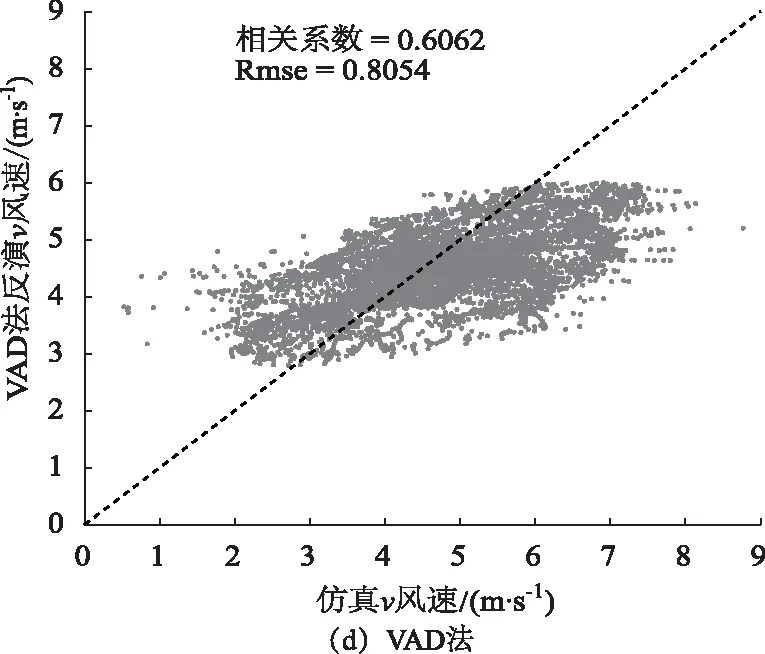
图4 仿真获取的风场水平分量和3D-VPP、VAD方法反演的结果的比较Fig.4 Comparison of wind field obtained by 3D-VPP and VAD method
2020年9月到11月,利用部署于长沙黄花机场的激光雷达开展了风场探测实验,激光雷达的系统参数及扫描策略见表1,按本扫描方式完成一次体积扫描需要约3 min。为了对本方法反演的水平风速进行验证,通过与在同一时间段、同一场地进行探测的探空气球观测数据进行比较,追踪气球轨迹获得不同高度上的水平风速以获得风速的廓线信息。
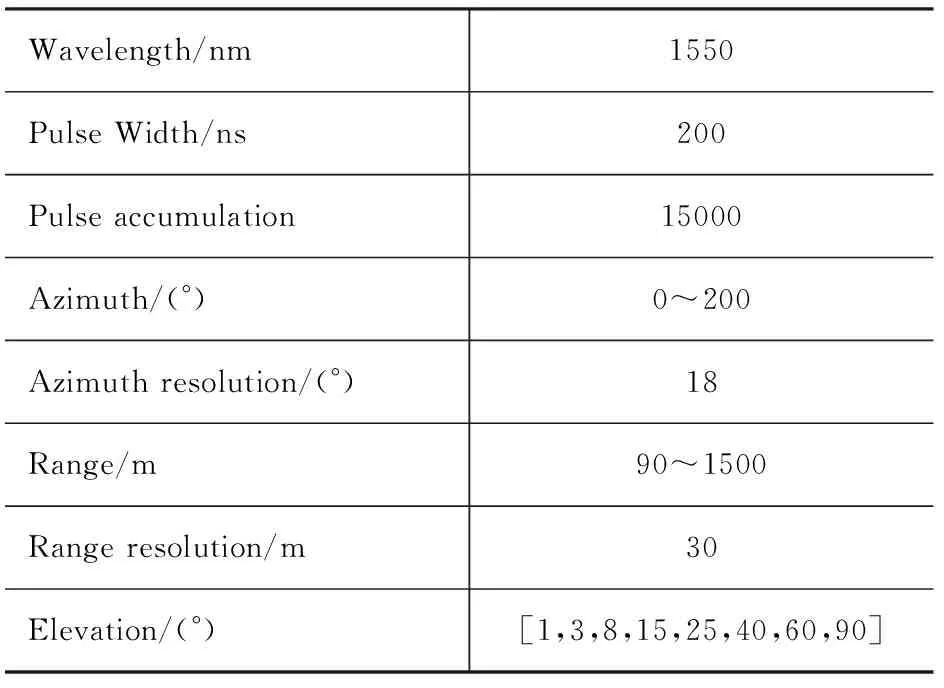
表1 外场实验中激光雷达的系统参数及测量参数Tab.1 System parameters and measurement parameters of Lidar
通过与探空气球测量得到的水平风速进行比较,验证反演算法反演水平速度的性能。图5中给出了探空气球和本方法得到的x,y方向上的水平风速的比较。横坐标为探空气球获得的水平风速的大小,纵坐标表示本方法反演得到的风速的大小,其中反演得到的u与探空气球数据的比较结果见图5(a),v的比较结果见图5(b)。可以发现对于水平速度的反演,采用3D-VPP方法可得到较理想的结果(与探空气球获取风速的一致性高),反演水平速度与探空气球实测速度相关系数均可达0.97以上(u方向为0.9866,v方向为0.9748),为进一步验证算法反演水平风速的性能,还需积累更多的探空气球数据。


图5 本算法反演得到的水平速度与探空气球数据的比较结果Fig.5 Comparison between the retrieved horizontal wind speed(u,v)and the pilot balloon observed data
3.2.2 风切变反演算法验证
激光雷达-降落点连线与飞机跑道夹角Θ小于30°,取跑道所在方位角上的3°高度角的径向速度作为飞机的迎头风。由于激光雷达只能直接获取径向风速数据,只有通过VVP、VPP以及变分法反演才能得到垂直风速,因此在过去关于下滑道风切变F因子的计算中,大多是采用忽略垂直风速,只考虑迎风梯度近似为F因子整体数值。如表2所示,若垂直风速与飞机进场速度(通常为75 m/s)比值大于0.1时,若此时仍忽略垂直项将导致误差增大,计算结果极易偏离真值,一旦超出国际惯例F因子±0.105风切变阈值,将会出现“虚警”或“漏警”情况,此时不能只考虑迎风梯度计算相应结果。

表2 风切变F因子在有、无垂直风速项的误差Tab.2 Errors of wind shear F factor with or without vertical wind speed
为提高计算精度,本方法加入通过3D-VPP方法反演得到的垂直风速,使计算结果更加贴近真实数值。如图6所示,该方法计算所得F因子与仿真结果高度吻合,相关系数超过0.98,均方根误差为0.013,而无引入垂直风速计算的F因子均方根误差大约是本方法的2倍,验证了使用本方法计算F因子具有较高的准确性,对于风切变预警具有较强应用价值。


图6 仿真获取的F因子强度和3D-VPP方法反演的F因子的比较Fig.6 Comparison of the F factor obtained by simulation and 3D-VPP method
3.2.3 湍流反演算法验证图
图7(a)、(b)给出了仿真风场和反演风场条件下,在35.3°高度角上采用部分傅里叶分解算法,计算所得的湍流动能强度高度廓线以及两者相关性情况。从仿真结果来看,两者具有较强相关性,均方根误差控制在0.03以内,在不同高度层两者变化趋势基本一致,且各高度误差均较小,因此采用本方法能够较准确地表征湍流动能强度情况。调整背景湍流场强度,按照强中弱3个等级,采用同样方法分析,分别得到图7(a)、(c)、(d),从3幅图中可以看出,无论在强中弱背景湍流场,采用本方法均能获得较好的湍流动能强度结果,反演误差均较小。但在强湍流条件下,如图7(d)所示,采用本方法获得的湍流动能强度均方根误差要远大于中弱湍流场环境,误差要大一数量级,因此本方法在中弱湍流强度情况下具有更佳的性能。
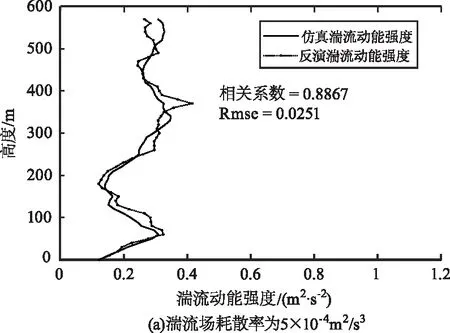



图7 仿真和反演计算所得湍流动能强度对比结果Fig.7 Comparison of turbulence energy intensity obtained by simulation and retrieval
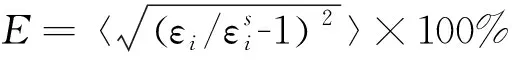

图8 仿真和反演计算所得湍流耗散率对比结果Fig.8 Comparison of turbulence dissipation rate obtained by simulation and retrieval method
比较本方法在不同湍流强度背景下的反演能力如表3所示,分别设置湍流耗散率为5×10-4m2/s3、1×10-3m2/s3、5×10-3m2/s3、1×10-2m2/s3背景湍流场,采用相同方法进行仿真和反演,可以看出本方法在中低湍流场条件下反演准确度都较高,相对误差能控制在25 %以内,在强湍流场背景下,使用本方法误差较大。

表3 仿真和反演湍流耗散率对比结果Tab.3 Comparison of turbulence dissipation rate obtained by simulation and retrieval method
4 结 论
本文提出一种晴空条件下的多用途的测风激光雷达体积扫描策略及风场特征获取方法,交替采用多个特定高度角的PPI扫描方式,通过3D-VPP方法由径向风速实现三维风场的反演。基于反演风场,在3°高度角下滑道区域,采用F因子强度评估风切变的存在;利用35.3°高度角圆锥扫描,采用部分傅里叶分解算法计算湍流动能强度;应用均匀湍流假设,计算径向速度结构函数,从而计算该区域湍流耗散率分布情况。
本文通过实验仿真,构建包含均匀风场、风切变以及湍流的背景风场,通过对比反演与仿真数据发现:本方法反演的三维风场与仿真风场吻合度较高,水平方向上反演精度更高;引入垂直风速计算风切变F因子,验证垂直风速与飞机进场速度(通常为75 m/s)比值大于0.1时,垂直风速项将对整体产生较大影响;采用部分傅里叶分解算法计算湍流动能强度时,在中弱湍流强度情况下具有更佳的性能;采用径向速度方位结构函数计算湍流耗散率时,在中弱湍流场时反演准确度较高,对于强湍流条件下湍流耗散率的反演方法,将在后续工作中进一步进行探索研究。
通过实验验证了本方法可有效兼顾空间覆盖范围、时空分辨率及鲁棒性,既能实现对飞机下滑道区域的重点探测,也能实现对于近场湍流强度的准确感知,还可实现对大范围三维风场的反演。
