智能牵引机动力系统功率匹配与自适应控制
2022-06-09
(1.华北水利水电大学 机械学院,河南 郑州 450045;2.河南电力博大科技有限公司,河南 郑州 450000)
引言
牵引机在国家电网高压输电架线施工过程中,有效的保障了施工质量以及施工效率。但牵引机工作环境较为恶劣,牵引的电缆线负载波动较大,导致发动机无法在最佳状态下工作,使发动机的输出功率与液压泵的吸收功率不匹配,无法实现自适应控制,造成油耗损失过大且影响工作效率。
目前,关于牵引机动力系统功率匹配的研究较少,大部分动力系统功率匹配的研究集中于液压挖掘机领域。在国内,王欣等[1]对发动机-液压泵功率匹配系统的关键部件进行分析,提出利用PID控制,通过检测液压泵和发动机的输出功率,按不同的工况分别对液压泵的恒功率设定值和发动机转速进行调节。杨世平等[2]利用数学建模的方法对挖掘机液压动力系统进行仿真分析,利用模糊控制实现了将发动机控制在目标转速附近,提高了发动机的燃油利用率。在国外,普遍采用电子控制技术,对发动机和液压泵同时进行检测和控制,并采用多段功率分档模式,达到动力总成功率匹配[3-6]。
综上所述,通过实现动力系统功率匹配与自适应控制来提高设备操作性能和降低油耗,已经引起广泛的研究和关注。但是,在国家电网现有施工装备中,关于牵引机的动力系统功率匹配与自适应控制研究仍存在很大空白。因此,本研究首先分析牵引机在工作过程中,导致动力系统功率不匹配的具体原因;随后对发动机和液压泵等关键元件及零部件进行原理分析,提出利用模糊控制策略解决动力系统功率不匹配存在的问题,并建立相应的模糊控制规则;最后利用MATLAB/Simulink分别建立发动机模型、液压泵模型和模糊控制器模型,将三者连接成简化的牵引机动力系统仿真模型,利用软件仿真证明动力系统加入模糊控制策略后,能有效解决现阶段动力系统功率不匹配的问题。
1 动力系统研究
牵引机动力系统的核心是发动机与液压泵,发动机驱动液压泵输出高压油,高压油再驱动液压马达带动牵引轮完成绳索牵引[7]。但导线的舞动导致牵引轮所受的负载不断变化,发动机从而出现严重的转速波动且油耗量急剧上升,有时甚至导致发动机熄火,不仅造成能源浪费还存在安全隐患。
1.1 牵引机动力传动系统
牵引机传动系统原理如图1所示,当牵引轮的负载产生波动时,波动转矩将经各个元器件传递到双向变量液压泵2,导致液压泵的负载随之变化,此时发动机1也会受到影响,由于发动机无法自主调整至合适的转速和转矩,可能导致其出现“大马拉小车”或“小马拉大车”的非正常工作状态[8]。
在架线施工现场,操作员通常根据经验判断负载的波动变化,手动控制油门旋钮使牵引机的工作状态满足施工要求。从负载波动产生到牵引机再次稳定工作,此过程中发动机转速波动较大,且未充分利用斜盘

1.发动机 2.双向变量液压泵 3.液压控制回路 4.牵引卷筒5.末级减速器 6.主减速器 7.制动器 8.双向液压马达图1 牵引机传动系统原理图Fig.1 Tractor transmission system schematic diagram
式轴向柱塞泵排量可调的特点去适应负载波动。
1.2 发动机工作特性
牵引机的发动机通常采用柴油发动机,柴油发动机的核心参数有转速、转矩、油耗量等。为进一步分析发动机工作特性,需根据发动机原理建立其数学模型,但由于发动机纯理论数学模型较为复杂,通常采用台架试验数据进行分析。基于某型号发动机[9]的台架试验数据,利用MATLAB软件绘制其三维曲面图形,如图2所示。
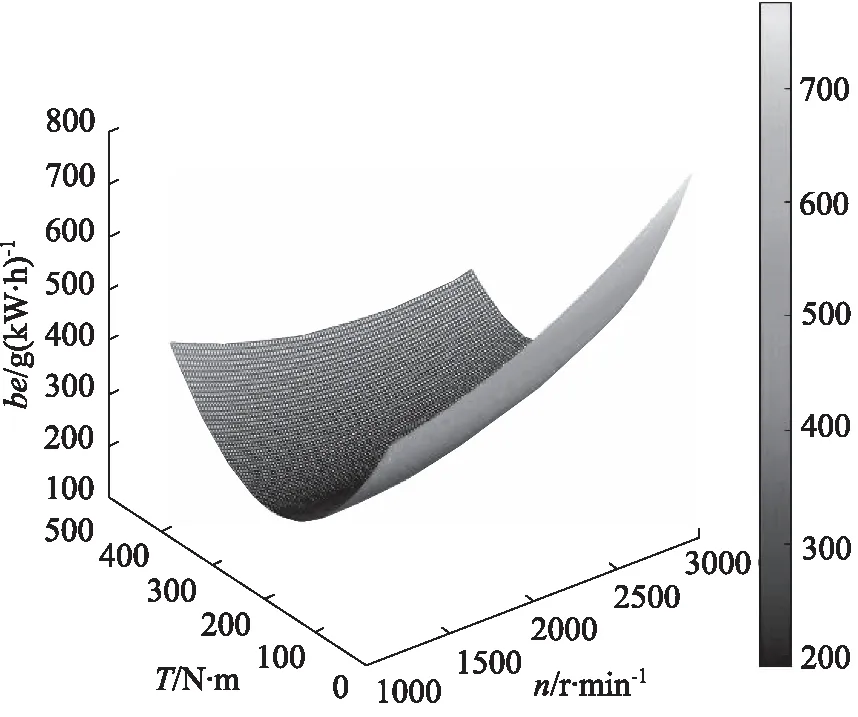
图2 等燃油消耗曲线三维拟合Fig.2 Equal fuel consumption curve 3D fitting
分析图2可知,若使发动机与液压泵完成功率匹配,且将发动机转速设定在最佳油耗曲线附近工作,同时使发动机满足牵引机对动力输出的要求,即可解决牵引机目前所遇到的技术难点。
发动机只需开机设定油门大小,即可完成由启动到稳定等一系列动作,若工作负载有波动(例如牵引机所牵引的绳索因外界环境变化,导致张力变大或变小),发动机所受到的负载转矩也会产生波动,此时发动机的机械式调速器会自行调速[10-11]。但是,牵引机的油门开度设定之后,即使工作负载发生波动,若传递到发动机的负载转矩未发生波动,则油门开度无需调节,只需控制传递到发动机的负载转矩即可稳定发动机转速。
如图3所示,当油门开度处于工作状态3时(状态1,2,3,4,5分别表示油门开度的5种程度),假设牵引机空载工作,则发动机转速稳定在n3处,当负载逐渐增大时,负载会沿着曲线3逐渐向C点、B点移动,相应的转矩由0 N·m增加至MeC,再增加至MeB。且研究表明,发动机调速特性与其转矩和油门开度有关[12],即:
Me=f(n,θ)
(1)
式中,Me—— 发动机的输出转矩
θ—— 发动机的油门开度
n—— 发动机的转速

图3 发动机调速曲线Fig.3 Engine speed curve
由于转矩、转速和油门开度之间的纯数学模型较为复杂,通常采用查表的方法确定,同时可根据达郎伯理论推导出柴油机工作时的动态数学模型,并与转矩模型结合建立发动机整机模型,其中发动机动态数学模型方程如下[13-14]:
(2)
式中,Md—— 发动机主转矩
Mc—— 负载转矩
J—— 发动机转动惯量
当牵引机的发动机所受负载转矩波动较小时,发动机掉速会导致发动机油耗量增加,偏离最佳工作点,影响施工效率。且发动机转速和转矩发生变化时,会导致发动机输出功率变化,进而产生发动机功率与液压泵功率不匹配的现象;当发动机负载转矩波动较大时,发动机掉速情况严重,可能导致发动机熄火,产生施工安全性问题。虽然油门开度对发动机转速起主导控制作用,但在牵引机稳定工作时,若无较大负载突变,油门开度通常希望保持不变。因此,当工作负载发生波动时,若在油门开度不变的情况下仍能保持发动机转速稳定,即可保证动力系统功率相匹配。
1.3 液压泵工作特性
牵引机通常采用斜盘式轴向柱塞变量泵,为分析斜盘式轴向柱塞泵的特性,以某型号变量泵为例进行分析,如图4所示。斜盘式轴向柱塞变量泵,最大的特点是可通过变量活塞缸双向调节泵的输出排量。补油泵给控制油路提供压力后,控制压力传递给控制阀,先导控制压力作用于Y1,Y2时,控制阀通过改变阀孔油路的开闭改变控制油压流动方向,压力油作用于变量活塞缸两端的活塞,使其两端产生压力差推动变量活塞动作,改变斜盘倾角使泵的排量发生变化[15]。而先导控制压力是可调节的,因此可以通过对控制阀的调节,改变液压泵的斜盘倾角,实现对液压泵排量的控制。
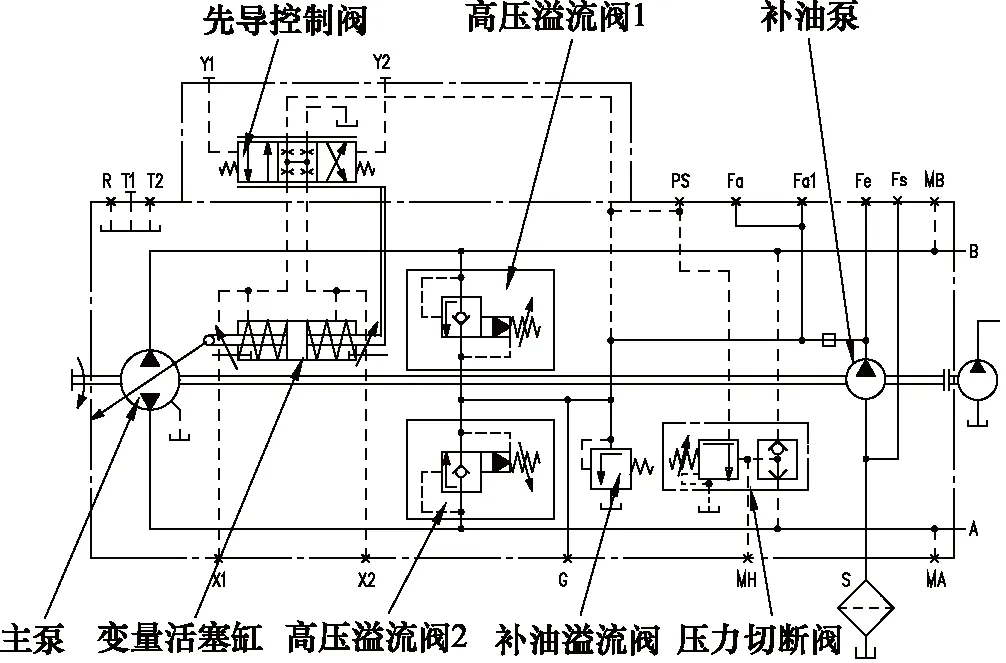
图4 某型号变量泵控制原理Fig.4 A type of variable pump control principle
变量泵的输出功率公式为:
P=pq=pVnp
(3)
式中,P—— 功率
p—— 压力
q—— 流量
V—— 排量
np—— 液压泵转速
变量泵通过联轴器与发动机直接相连,通常与发动机转速相同[16]。
变量泵的排量可按下式计算:
(4)
式中,d—— 柱塞缸直径
D—— 柱塞在刚体上的分布圆直径
δ—— 斜盘倾角
z—— 柱塞数(一般常规柱塞数取7,9或11)
变量泵的输出转矩公式为:
(5)
式中,M—— 变量泵的实际输出转矩
η—— 机械效率(通常取0.92~0.96)
当负载产生波动时,导致液压泵出口压力p发生变化,排量q保持不变时,根据式(3),可知液压泵的功率P则发生变化,此时负载波动直接导致了液压泵的功率发生波动。
综上所述,由于负载波动导致液压泵出口压力和功率发生变化,一方面使发动机远离最佳工作点;另一方面使发动机输出功率改变,导致液压泵功率与发动机功率不匹配。若能在工作负载发生波动时,保持油门开度不变的情况下,通过改变液压泵排量V,使发动机所受到的负载转矩保持不变,进而使转速保持稳定(始终在最佳工作点附近),同时保证牵引机能满足工作负载施工要求,即可实现牵引机动力系统功率匹配和自适应控制。
2 动力系统匹配建模分析
牵引机动力系统匹配核心在于调节转速稳定,同时使设备自动满足施工负载变化要求。当发动机输出功率一定时,则假设液压泵的输入功率保持不变,此时斜盘式轴向柱塞泵可通过改变排量V去适应液压泵出口压力p的变化(出口压力p由负载决定)。因此系统建模的核心即为调节液压泵的排量V,使其能在负载多变的情况下自动调节,从而间接稳定发动机转速,实现牵引机动力系统功率匹配与自适应控制。
2.1 发动机与液压泵的功率匹配策略
如图5所示,当牵引机启动之后,且保持一定的油门开度,牵引机尚未开始进行牵引工作,此时发动机空载运行,转速处于n0点。当负载逐渐增大至稳定时,发动机处于A点且稳定工作,假设此时为最佳工作点,发动机转速为nA,转矩为MeA,功率为PE.A,液压泵处于A′点且稳定工作,液压泵流量为qA′,出口压力为pA′,功率为PA。
当牵引机负载发生波动时(以负载增大为例),此时液压泵出口压力增大,即液压泵工作点由A′移动到点B′,液压泵流量不变仍为qA′,出口压力由pA′变成pA″,液压泵功率由PA变为PB。发动机由于负载转矩发生变化,需减速增矩满足工作负载需求,工作点由A点移动到B点,转速由nA降低到了nB,发动机输出功率由PE.A变为PE.B,根据发动机油耗模型可知,发动机将远离最佳工作点。
负载发生波动时,虽然液压泵与发动机的功率同时发生了变化,但仍存在2个问题:①二者功率无法像A点与A′点稳定状态时的正常匹配,此时功率匹配发生了波动;②未充分利用斜盘式轴向柱塞泵排量可调的特性,并且新工作点增加了发动机的油耗量,可能出现“大马拉小车”的现象。
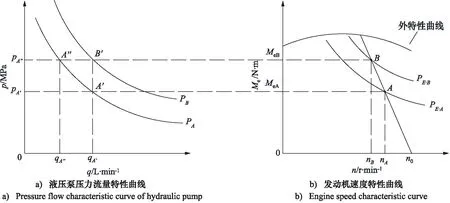
图5 发动机与液压泵功率匹配Fig.5 Engine and hydraulic pump power matching

表1 控制策略Tab.1 Strategy making
可以通过调节流量,使液压泵工作点由B′移动到A″,此时液压泵功率再次变为PA,由于液压泵是通过改变流量满足工作负载要求的,则发动机的负载转矩就无需变化,无需发动机进行减速增矩,因此发动机负载转矩可再次变回MeA[17]。发动机与液压泵工作点整个动态变化过程如表1所示。
2.2 控制系统模型建立
由式(3)和式(4)可知,液压泵在使用过程中,当转速一定时液压泵的流量q由斜盘倾角δ决定,即公式为:
(6)
式中,q—— 流量
d—— 柱塞缸直径
D—— 柱塞在刚体上的分布圆直径
δ—— 斜盘倾角
z—— 柱塞数(一般常规柱塞数取7,9或11)
η—— 机械效率(通常取0.92~0.96)
将牵引机负载波动看作自变量,经过中间环节液压泵的处理,则发动机转速为因变量。因此可以通过检测因变量(发动机转速)的变化,将变化结果作为反馈去调节中间环节液压泵的特性参数,形成一个闭环控制系统,最终实现因变量的稳定控制。结合发动机与液压泵的硬件特性,提出控制方案如图6所示。
发动机油门开启之后且工作负载较稳定时,转速将稳定在发动机提前设置好的最佳工作点,同时需根据不同发动机的特性,在不同油门开度下均设置一个最佳目标转速。若负载发生波动时,可以通过传感器数据计算出当前转速与目标转速的差,并将转速差作为控制器调节液压泵比例电磁阀的依据。在比例电磁阀的控制下,柱塞泵斜盘倾角δ发生变化并改变排量,此时液压泵所需的输入转矩将逐渐恢复初始状态。

图6 控制系统原理Fig.6 Principle of control system
液压泵输入转矩由发动机输出转矩提供,当液压泵所需输入转矩逐渐恢复时,发动机输出转矩也将逐渐恢复初始稳定状态,当发动机输出转矩逐渐变化时,则发动机转速将沿着调速特性曲线(图3)逐渐变化,直至转速与转矩稳定下来。因此,通过控制液压泵排量的变化,间接调节发动机的输出转矩,使转速按照调速特性曲线变化,进而调节发动机转速稳定,是控制系统的核心。
2.3 功率匹配核心控制算法
若利用传统控制方法对某个系统进行控制时,需要建立控制系统的数学模型、模型的结构、阶次等参数[18]。仔细分析牵引机动力系统,发动机与液压泵的数学模型建立起来较为复杂,无法建立较为精确的数学模型。对于数学模型十分复杂的控制系统,可以采用模糊控制的方法实现对系统的控制[19-21]。模糊控制系统的建立主要包括输入变量和输出变量、模糊子集隶属函数、模糊控制算法规则以及比例因子。

表2 输入输出模糊子集Tab.2 Input and output fuzzy subsets

表3 模糊控制规则表Tab.3 Fuzzy control rule table
此模糊控制设计的输入变量选取发动机转速差E和转速差的变化率EC,输出变量是控制变量泵排量变化的斜盘倾角δ,隶属函数选取三角形隶属函数。其中发动机转速差E选定8个模糊子集,转速差的变化率EC选定7个模糊子集,斜盘倾角δ选定7个模糊子集,如表2所示。
利用模糊控制系统可将发动机与液压泵建立联系[21],解决动力系统功率匹配目前存在的问题。
3 基于MATLAB/Simulink模型仿真分析
根据牵引机操作员的经验指定模糊规则,其中模糊控制规则如表3所示。
由于牵引机的发动机与液压泵功率匹配现场试验建立较为复杂,若缺乏正确的理论指导会浪费大量的人力物力。因此利用Simulink仿真模型对发动机和液压泵进行数学模型的建立[22],一方面能简化整体系统模型的搭建,提高牵引机动力系统的设计速度,为搭建现场试验模型提供理论依据;另一方面能验证模糊控制算法,对比加入控制算法之后是否达到预期效果。
3.1 发动机Simulink模型建立
柴油发动机转轴的主转矩与油门开度有关,若建立油门开度与主转矩的理论数学关系较为复杂,可利用发动机台架试验数据,根据式(1)、式(2)建立Simulink查表功能,能极大减少建模工作量并达到预期效果,发动机仿真模型如图7所示。

图7 发动机仿真模型Fig.7 Engine simulation model
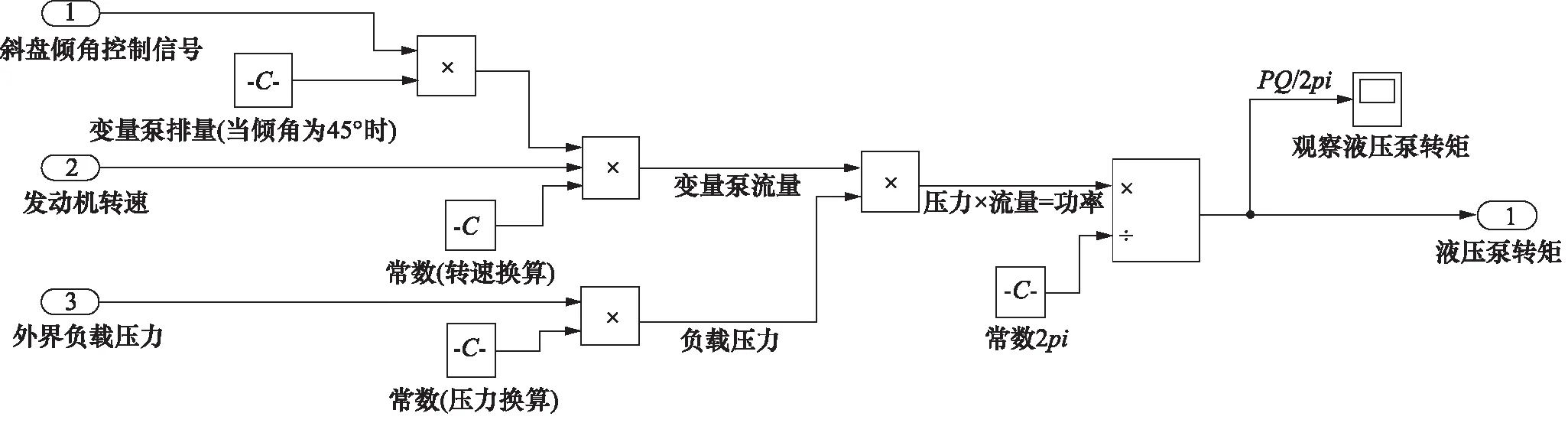
图8 液压泵仿真模型Fig.8 Hydraulic pump simulation model
3.2 液压泵Simulink模型建立
由于变量泵主要由先导压力控制阀、伺服电液比例阀、斜盘等主要零部件组成,因此需对其进行原理分析与数学模型的建立,之后再利用拉普拉斯变换求出其传递函数,得出较为精确的机电液控制系统关系[23-24]。由于功率匹配核心在于匹配策略与控制算法是否可行,对于变量泵的仿真模型而言,建立一个根据输入液压泵转速、外界负载和斜盘倾角控制信号,输出液压泵转矩即可。因此可根据式(3)~式(6)建立简化后的变量泵仿真模型,仿真模型如图8所示。
3.3 牵引机动力系统功率匹配仿真模型
整个动力控制系统核心主要分为三部分:发动机、液压泵和模糊控制器。仿真模拟按牵引机现场施工操作员的操作进行,输入条件为油门开度(保持油门开度在某一开度下)、发动机目标转速(根据不同的油门设置不同的目标转速)、牵引机所牵引的外界负载,需实时监测发动机实际转速,观察其是否发生波动、是否稳定在目标转速附近。牵引机动力系统功率匹配与自适应控制系统仿真模型如图9所示。
3.4 仿真结果分析对比
仿真条件将油门开度设置为80%,发动机目标转速设定在1300 r/min,仿真时间设定为10 s,在1.5,3.8,7.0 s附近分别给液压系统加入模拟负载干扰信号,模拟负载干扰信号设置如图10所示,得到的仿真结果如图11所示,图11a为未加入控制算法时的仿真结果,图11b为加入控制算法后的仿真结果。
对比仿真结果可以得出,未加入控制系统时,负载导致发动机转速波动范围较大,与牵引机实际工作情况一样,转速在1250~1360 r/min范围内变化。加入控制系统以后,转速基本稳定在1300 r/min,波动较小。

图9 动力系统功率匹配与自适应控制仿真模型Fig.9 Power matching and adaptive control simulation model of powertrain

图10 负载波动信号Fig.10 Load fluctuation signal
4 结论
(1) 通过对发动机与液压泵的工作特性分析,根据发动机台架试验数据和变量泵的结构参数,建立了发动机与液压泵的数学模型,为牵引机动力系统功率匹配的设计提供了理论基础;
(2) 根据动力系统功率匹配原理,提出通过检测发动机转速变化并建立相应的模糊控制规则,利用模糊控制系统控制液压泵排量变化,使动力控制系统形成一个闭环控制系统,以保持发动机转速稳定;
(3) 利用Simulink软件建立牵引机动力系统整体仿真模型,成功验证了加入模糊控制系统后,在工作负载发生波动时,发动机能自主适应负载变化并将实际转速稳定在目标转速附近,解决了发动机动力系统功率不匹配的问题。

图11 发动机输出转速Fig.11 Engine output speed
