水平冷凝管在水膜作用下稳态传热数值模拟

钱颖燕 周亚素 张恒钦

1 东华大学环境科学与工程学院

2 上海良机冷却设备有限公司

1 引言

蒸发式冷凝器可以看作是将水冷式冷凝器和冷却塔结合的高效换热设备。它利用水膜蒸发将管内制冷剂冷凝时的热量带走，再通过空气强制对流排出热量，具有节能、节水、冷凝效果好，占地面积小等优[1]。目前，国内外研究人员对蒸发式冷凝器也进行了大量的研究工作。从文献[2～5]可以知道对于蒸发式冷凝器管外水膜的研究较多。从唐广栋[6]的研究可以得出，不考虑污垢热阻，管内冷凝热阻大约占了总热阻的25%～35%，水膜热阻约占了25%～40%，气液界面热阻约占23%～40%，而管内冷凝热阻和水膜热阻是比较容易通过手段减小的两个热阻，因此也有必要对蒸发式冷凝器管内冷凝换热进行研究。而对于水平管内冷凝，开展的换热性能研究[7～15]多为一侧为制冷剂，另一侧为冷却水或空气，很少涉及管外降膜蒸发换热的研究。

基于此，本文运用 EES（Engineering Equation Solver）软件编程计算，模拟水膜作用下水平冷凝管内换热性能，研究了冷凝管长度和冷凝温度对出口干度，换热量和管内换热系数的影响，为蒸发式冷凝器的设计及性能优化提供一定的参考。

2 水膜作用下水平冷凝管模型

水平冷凝管在水膜作用下的传热过程主要可分为两个阶段，第一阶段是管内制冷剂冷凝放出热量，并通过管壁将热量传递给管外水膜。第二阶段则是管外水膜将热量传递给空气，这是一段复杂的传热传质过程。

制冷剂在冷凝管内一般由过热区、两相区和过冷区组成。本文采用分布参数模型对水膜作用下的水平冷凝管进行稳态建模。按制冷剂流动方向沿管程将换热管划分为若干个微元段，选这些微元段为控制体进行求解。

2.1 模型假设条件

为了简化模拟，需要做出以下假设：

1）管内制冷剂沿轴向作一维流动，不用考虑径向流动。

2）管内制冷剂冷凝温度为一定值[16]。

3）忽略轴向导热，只考虑径向换热。

4）忽略不凝性气体影响。

5）忽略管内外污垢热阻的影响[16]。

6）制冷剂进口蒸汽为对应压力下的饱和气体。

7）管外喷淋水和空气均匀流过冷凝管。

2.2 基本换热方程

水膜作用下冷凝管段的简化模型如图1 所示。按制冷剂流动方向沿管程将冷凝管划分为若干个微元段，微元段示意图如图2 所示。

图1 水膜作用下冷凝管段物理模型示意图

图2 水膜作用下冷凝管微元段示意图

1）微元段制冷剂侧换热方程式可表示为：

式中：Qc为总换热量，kW；mr为制冷剂蒸汽流量，kg/s；hri为入口制冷剂蒸汽的比焓，kJ/kg；hro为出口制冷剂液体的比焓，kJ/kg。

2）管内制冷剂换热量经过管壁传递给管外水膜，最终热量由空气带走。

微元段换热量可表示为：

式中：K为制冷剂到管外空气的总传热系数，W/(m2·K)；A0为总的传热面积，m2；tr为微元段管内制冷剂侧平均温度，℃；twa为空气的平均温度，℃。

忽略污垢热阻后的制冷剂到管外空气的总传热系数可表示为下式：

式中：αi为管内流体对流换热系数，W/(m2·K)；do为换热管外径，m；di为换热管内径，m；λ为管材的导热系数，W/(m2·K)；αw为管壁与水膜间的传热系数，W/(m2·K)；αj为水膜与空气之间的当量对流换热系数，W/(m2·K)。

根据以上公式，由于能量守恒，可以推导出水膜作用下冷凝管微元段长度dL的计算式：

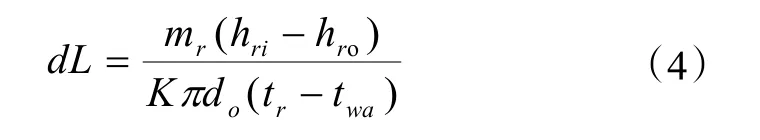
2.3 换热系数的计算

1）管内制冷剂侧换热系数αi

对于单相区，管内制冷剂侧换热系数采用 Dittus-Boelter[17]公式来计算：

式中：αi为管内流体对流换热系数，W/(m2·K)；Gr为制冷剂质量流速，kg/(m2·s)；μr为制冷剂动力粘度系数，Pa·s；λr为制冷剂导热系数，W/(m·K)；cp,r为制冷剂比热容，J/(kg·K)。

对于两相区，管内制冷剂侧换热系数则可按下式计算[18]：

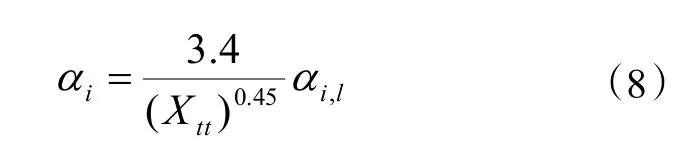
Xtt为两相区换热修正系数，计算可按下式：

式中：αi,l为全部为液体时制冷剂的换热系数，W/(m2·K)，按式（5）计算；x为制冷剂的干度；ρr,v、ρr,l分别是制冷剂气相和液相的密度，kg/m3)；μr,v、μr,l分别是制冷剂气相和液相的动力粘度，Pa·s。

2）管壁与水膜间换热系数αw

Parker 和 Treybal[19]在 McAdams[20]等人得出的管壁与水膜之间的换热关系式的基础上，进一步得出了适用于水平管管外水膜与管壁之间的换热，可如下表所示：

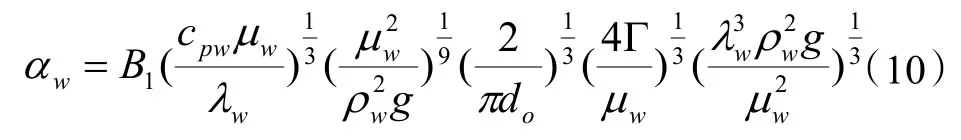
式中：B1为常数，本文取0.332；cpw为喷淋水的定压比热容，kJ/(kg·K)；μw为水的动力粘度，kg/(m·s)；λw为水的导热系数，W/(m·K)；ρw为水的密度，kg/m3；g为重力加速度，m/s2；Γ 为管外喷淋水的喷淋密度，kg/(m·s)。

3）水膜与空气之间的当量对流换热系数αj

张祉祐[21]针对管外水膜与空气间的换热，把喷淋水与空气的换热看成是显热交换和潜热交换两部分作用，并在此基础上引入当量换热系数，以便与管内流体和管外水膜间的传热系数统一起来。

水膜与空气对流换热系数关联式为：

式中：C，m为常数，与空气流动状态 Rea和管束排列方式有关，本文C取0.52，m取0.5；Pra则为空气的普朗特数。

根据文献[21]可得出当量换热系数αj表达式为：

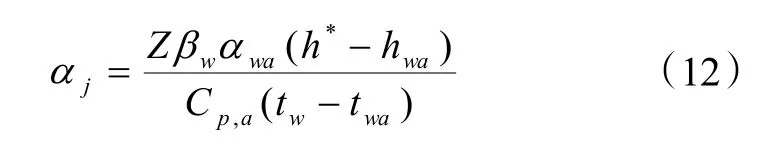
式中：Z为与喷淋水膜有关的系数，本文取0.96；βw是水膜与空气间接触面积的修正系数，取1.3～1.5；h*是与喷淋水温度相对应的饱和空气的比焓，kJ/kg；hwa为湿空气的平均比焓，kJ/kg；Cp,a为湿空气的比热，kJ/(kg·℃)；twa为空气的平均温度，℃。

3 理论计算流程

本文模拟的水平冷凝管相关参数如表1：

表1 水平冷凝管相关参数

计算中给定管外喷淋水喷淋密度为0.047 kg/(m·s)，喷淋水温21℃，空气干球温度25℃，湿球温度19.5℃，迎面风速2.9 m/s。

模拟计算所用的稳态分布参数模型程序中所用的迭代算法为二分法。具体的算法过程如下：

1）假设制冷剂出口焓值hro。以给定冷凝压力的制冷剂饱和气体焓值作为二分法的上限，喷淋水进口温度下的制冷剂液体焓值作为二分法的下限。取上下限值的算术平均作为制冷剂出口焓值的迭代初始值。

2）从冷凝管出口开始对微元段进行编号计算。

3）将假定的制冷剂出口焓值和冷凝温度所对应的饱和制冷剂液体焓值比较。如果出口焓值小于饱和液体焓值，则制冷剂处于过冷状态，计算过冷区长度。反之，制冷剂处于两相状态，计算两相区长度，将过冷和两相区中每个微元段长度相加得到冷凝管计算管长。

4）将计算管长与实际管长进行比较。如果计算管长大于实际管长，说明假设焓值过小，则以假定焓值取代二分法的下限。如果计算管长小于实际管长，说明假定焓值过大，则把二分法的上限替换成假定焓值，重新计算，即转向（2），假定焓值根据算数平均值计算。如果满足要求，则结束计算，输出结果。

具体计算流程图如图3：

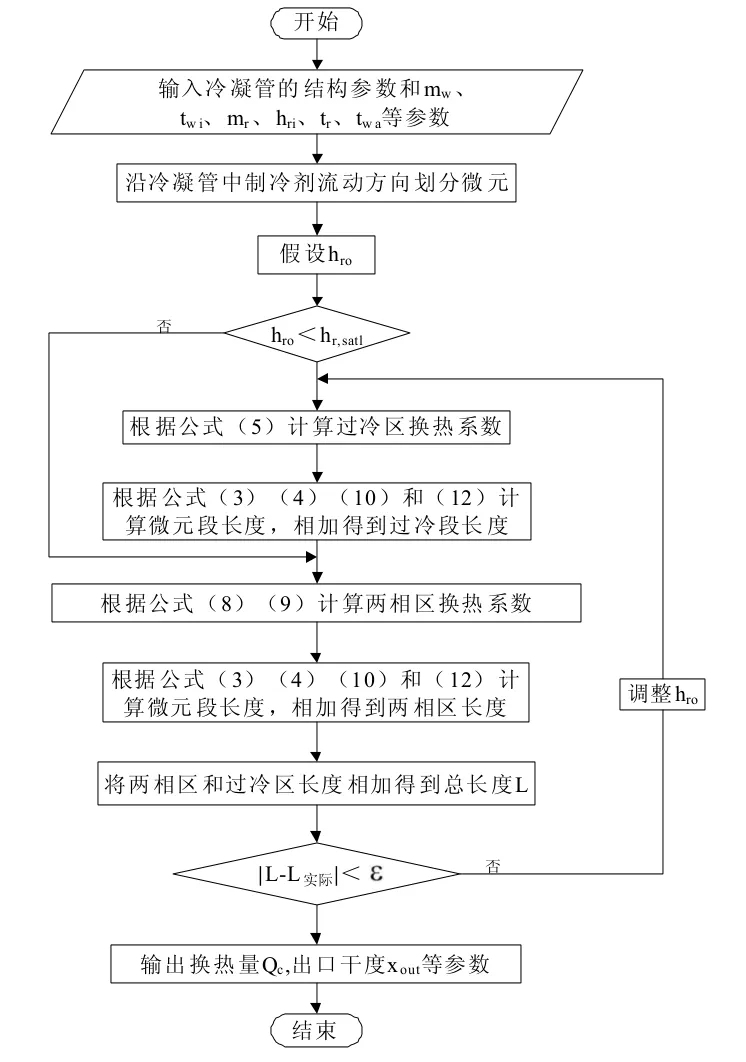
图3 水膜作用下水平冷凝管数值计算流程图

4 数值计算结果与分析

4.1 冷凝管长度对出口干度，换热量及管内平均换热系数的影响

本节在冷凝温度40℃的条件下，模拟了不同冷凝管长度（4～5.7 m）对出口干度，换热量及管内平均换热系数的影响。

对于冷凝器而言，选择合适的管长使冷凝管出口干度达到0，可以有效降低铜的用量和成本，同时也降低了能耗，提高经济性。图4 所示为水平冷凝管长度对出口干度的影响，由图可知，冷凝管出口干度随着管长的增加不断减小。由于冷凝管越长，相同制冷剂质量流量下换热时间越长，换热越充分，因此出口干度越小。制冷剂质量流量从0.0044 kg/s 增加到0.0078 kg/s，冷凝管长度增加35.7%，才能使出口干度达到0，在其它参数不变的条件下，当制冷剂质量流量增大时，主流速度也增大，制冷剂蒸汽与管壁之间换热不充分，出口干度增大，因此需要增加管长来延长换热时间使制冷剂蒸汽充分冷凝。

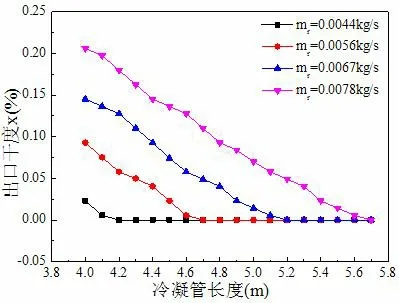
图4 冷凝管长度对出口干度的影响

图5，图6 分别为水平冷凝管长度对管内平均换热系数和换热量的影响。从图中可得知：随着冷凝管长度增加，管内平均换热系数基本不变，波动范围在4 W/(m2·K)内。换热量随冷凝管长度增加先不断增大，后增加趋势变缓。当管长增到一定长度时，出口干度达到0，管内制冷剂已全部冷凝成液体，继续增加冷凝管长度，长度增加部分的换热从潜热换热变成显热换热，换热量较小，因此换热量增加幅度变小。在制冷剂质量流量为0.0078 kg/s 时，管长从4 m 增加到5.7 m，换热量增大了26.4%。

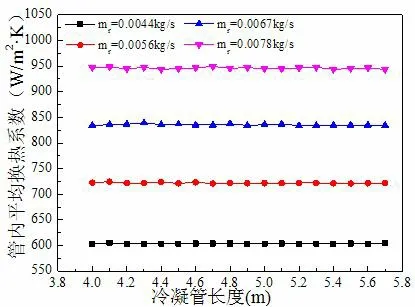
图5 冷凝管长度对管内平均换热系数的影响

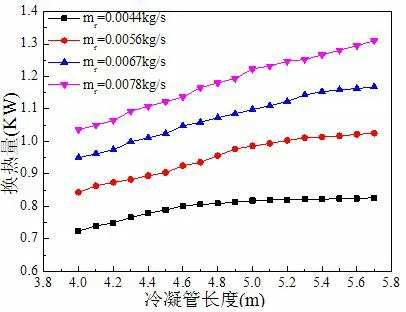
图6 冷凝管长度对换热量的影响

4.2 冷凝温度对出口干度，换热量及管内平均换热系数的影响

在管长为4.6 m 的条件下，模拟了不同冷凝温度（35℃～42℃）对出口干度，换热量及管内平均换热系数的影响。

图7 所示为不同制冷剂质量流量下，冷凝温度对出口干度的影响。

从图7 中可以看出，冷凝温度越高冷凝管出口干度越小，因为冷凝温度升高导致传热温差变大，增加了传热驱动力，加强了换热效果，所以出口干度减小。在制冷剂质量流量为0.0078 kg/s 时，冷凝温度从35℃增加到42℃，出口干度减小了88.7%。

图7 冷凝温度对出口干度的影响

图8 为不同制冷剂质量流量下，冷凝温度对换热量的影响。

图8 冷凝温度对换热量的影响

从图8 中可以看出：

1）同一冷凝温度下，换热量均随着制冷剂质量流量的增大而增大。因为质量流量增大使得制冷剂流速增大，气液界面剪切力变大，液膜变薄，热阻变小，从而增强了换热效果。在冷凝温度为40℃时，制冷剂质量流量从0.0044 kg/s 增加到0.0078 kg/s，换热量增加了42.5%。

2）制冷剂低质量流量下，冷凝温度对换热量的影响比高质量流量下的影响小。当质量流量为0.0044 kg/s 时，冷凝温度从35℃增至42℃，换热量增加了34.4%；当质量流量为0.0078kg/s 时，冷凝温度从35℃ 增至42℃，换热量增加了48.2%。这是因为随着冷凝温度升高，传热温差增大，增大了传热驱动力。在低质量流量下，随着冷凝温度升高，制冷剂蒸汽密度增大，导致流速降低，冷凝液膜厚度增加，热阻增大，会减小换热量，但相对而言，传热温差对换热量的增加作用更强，因此换热量随着冷凝温度升高而增大。而在高质量流量下，冷凝温度变化对液膜厚度影响不明显，所以高质量流量时，换热量随冷凝温度的变化趋势比低质量流量时明显。

图9 是不同制冷剂质量流量下，冷凝温度对管内平均换热系数的影响。

图9 冷凝温度对管内平均换热系数的影响

从图9 中可以看出：

1）其它参数条件不变时，管内平均换热系数随制冷剂质量流量的增大而增大，冷凝温度为40℃时，质量流量从0.0044 kg/s 增加到0.0078 kg/s，管内平均换热系数增加了56.8%。

2）与换热量相反，其它参数不变时，管内平均换热系数随冷凝温度的升高而减小。在制冷剂质量流量分别为0.0044 kg/s，0.0056 kg/s，0.0067 kg/s 和0.0078 kg/s 时，冷凝温度从35℃增至42℃，管内平均换热系数分别减小了7.14%，7.30%，7.29%和6.48%。

5 结论

本文利用 EES 软件模拟计算了在水膜作用下水平冷凝管的换热情况，得出如下结论：

1）冷凝管出口干度随着管长的增加不断减小。当制冷剂质量流量从0.0044 kg/s 增加到0.0078 kg/s 时，冷凝管长度增加35.7%，才能使出口干度达到0。管内平均换热系数随冷凝管长度增加基本不变。换热量随冷凝管长度增加先不断增大，后增加趋势变缓。当制冷剂质量流量为0.0078 kg/s 时，管长从4 m 增加到5.7 m，换热量增大了26.4%。

2）冷凝温度越高冷凝管出口干度越小。在制冷剂质量流量为0.0078 kg/s 时，冷凝温度从35℃增加到42℃，出口干度减小了88.7%。制冷剂低质量流量下，冷凝温度对换热量的影响比高质量流量下的影响小。当质量流量为0.0044 kg/s 时，冷凝温度从35℃增至42℃，换热量增加了34.4%。当质量流量为0.0078 kg/s 时，冷凝温度从35℃增至42℃，换热量增加了48.2%。与换热量相反，其它参数不变时，管内平均换热系数随冷凝温度的升高而减小。