沿程加热气泡泵流动沸腾模拟研究
2022-06-09孔则赟杨洪海段文利陈玉萍黄欣宇
孔则赟 杨洪海 段文利 陈玉萍 黄欣宇
东华大学环境科学与工程学院
1 引言
气泡泵是无泵吸收式制冷循环的核心部件。图1 为气泡泵运行示意图。工作流体由低位储液器进入气泡泵底部,工质受热气化形成气液两相流,在压差和浮力共同作用下将工作流体提升到高位储液器,高位储液器的循环工质再流回低位储液器,形成一个循环[1]。
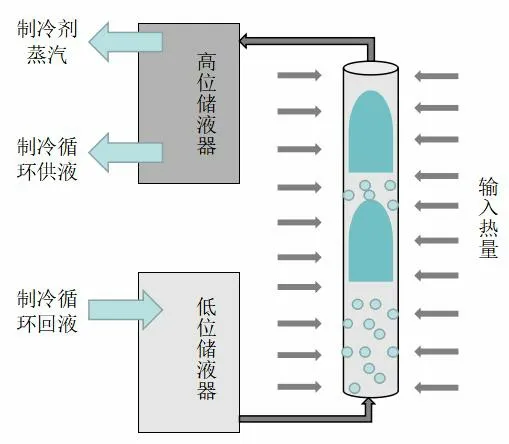
图1 气泡泵运行原理的示意图
目前,国内外学者对于沿程加热在实验研究方面:B ernd[2]进行了不同加热类型对气泡泵的泵送性能影响的实验研究,结果表明加热类型对泵送性能有很大影响。加热的相对长度越短,泵送比就越高。Pfaff[3]研究了溴化锂-水吸收式制冷机中气泡泵的震荡问题。研究发现减小气泡泵提升管内径、增大加热功率、气泡泵的震荡周期缩短。实验研究有其局限性,尤其是在加热方式和可视化方面很难做到两全其美,而数值模拟研究能有效应对这个问题。Benhmidene[4,5]建立了在恒定热流下沸腾混合氨水的一维双流体模型,运用数值模拟气泡泵在不同管径和热流密度下性能进行研究,发现最佳运行工况下热流密度管径有关。S oo W.Jo[6]在 Benhmidene 基础上采用双流体模型进行多维数值模拟,发现热流密度越高或者直径越小时泵送比越高。
沿程加热气泡泵实际运行中的加热量以及进口质量流量与管径耦合。所以本文在现有研究基础上,以水为工质,采用CFX-19 建立二维模型研究沿程加热气泡泵流动沸腾情况,并进一步研究最佳加热量与管径和进口质量流量的关系。
2 控制方程及计算模型建立
本研究采用两流体模型,关键需要湍流方程封闭,解决此封闭模型需要:相间动量,相间能量,相间质量传输模型及壁面沸腾模型。由于双流体模型所涉及的方程数量很多,为节省计算成本,通常采用迭代算法,即先求解动量方程,然后在此基础上求解其他方程。因此动量方程的准确性就直接或间接地决定了整个数值计算结果的准确性。
2.1 相间动量传输方程
气液两相间的动量运输表示为界面力的形式,界面力包括曳力FD和非曳力,其中非曳力包括升力FL、壁面润滑力FW和湍流耗散力FTD等。单位体积内两相间总的作用力为以上力之和,取l或v分别表示液相和气相:
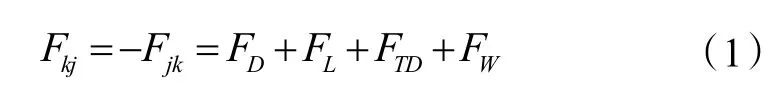
式(1)中右侧各项则参照文献[11-12]推荐的公式计算。
2.2 相间质量传输方程
在气泡泵中气相由液相汽化产生,液相只要达到运行压力下的饱和温度即可产生气泡,反之冷凝。假定气相在两相流中始终处于饱和温度,传热传质发生在气液两相的界面上。质量传输有用户自定义质量传输,质量传输选择热相变模型,并给定其饱和温度。单位体积内相间传质速率表示为:

式中:Avl表示气液两相界面面积,Tsat表示饱和温度,hvl为气液两相界面处焓值。
2.3 相间能量传输方程
气液两相间的质量,动量和能量都是通过两相界面进行传递,由于产生的气泡弥散在液相中,因此将气相看作离散相,液相看作连续相。界面传热模型选用 Two Resistance Model 模型。连续相选择 Ranz-Marshall 模型,离散相选择zero resistance 模型。Ranz-Marshall 的关系式为:
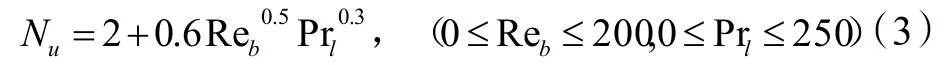
式中:Re为雷诺数,Pr为普朗特数。
2.4 壁面沸腾模型
ANSYS CFX 采用 Kurul 等提出的壁面热流分配模型,即伦斯勒理工模型(RPI:R ensselaer Polytechnic Institute)[13],模型对汽化核心密度、气泡脱离直径、气泡脱离频率、气泡等待时间等进行了描述。通过固体壁面传递给流体的总热流量Qwall分为三部分:对流传热QF,淬冷传热QQ及蒸发传热QE。

由于所研究的气泡泵是以中心线为轴对称的竖直圆管,本文主要研究在轴向方向上的物理特性,不关注圆周方向变化,可以假定在圆周方向上物性参数梯度为零。另外,取1/4 垂直圆管为计算域来模拟整根垂直管,这样可以减少网格数量,降低计算量,在两个对称切面上设置对称边界条件,忽略管壁厚度,模型如图2 所示。采用 ANSYS 中的 ICEM CFD 软件对模型进行网格划分,竖直管整体采用六面体网格划分,使模拟更加容易收敛。高度方向上网格长度为1 mm,进出口采用Y 形网格划分从而提高网格质量,壁面处网格进行了适当加密,宽度加密为0.1 mm,网格总数量46 万。当能量方程的残差值小于10-4时认为计算结果达到要求。进口处网格分布如图3 所示。
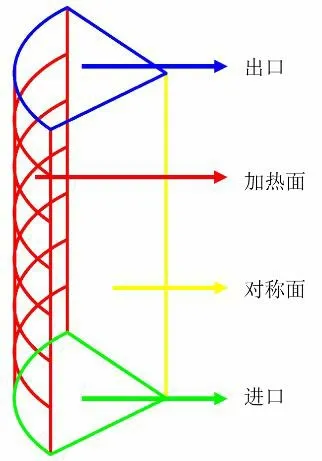
图2 模型简化示意图

图3 进口处网格划分示意图
在竖直管道入口处的质量流量和温度设为均匀分布,出口设定压力边界条件。壁面上气泡在生成过程中存在滑移现象而不受剪切力作用,而液相在边界层满足无滑移条件。
在研究以水为工质的气泡泵文章中,沿程加热式气泡泵管长一般在1000 mm[6-8],4~16 mm[9-11]的管径被学者所研究,其中6~12 mm 的管径较为符合实际应用,进口质量流量多在10~90 kg/m2·s[4-6,9]。综合考虑本文研究问题,结合学者研究以及实际应用,所以气泡泵参数如表1 所示。

表1 气泡泵模拟的参数
3 模型验证
为证明本论文采用的模型具有合理性,需验证模型有较高的准确性,将 Raoudha Garma[12]模拟方案带入本论文采取的模型进行数值建模计算,具体参数见表2,并将得到的结果与 Raoudha Garma 的结果进行对比,对比工况如图4、5 所示。
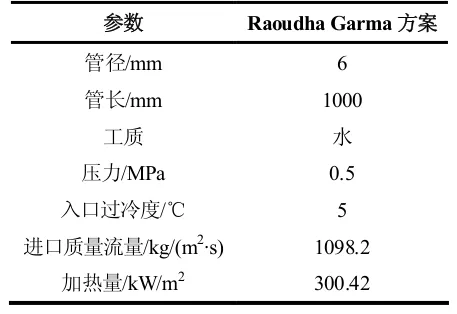
表2 验证工况参数表

图4 空泡份额模拟结果对比

图5 速度模拟结果对比
由图4、5 中可以看到,两者的变化趋向基本一致,因此,建立该模型可以用来进行下一步研究。
4 模拟结果与分析
4.1 出口液相表观速度分析
在不同管径(D=6、8、10、12 mm)、不同进口质量流量(G=20、40、60、80 kg/(m·2s))、不同热流密度下(0.5~ 75 kW/m2),模拟出口液相表观速度的变化,然后将模拟的结果数据进行拟合,探究不同管径不同热流密度的出口表观速度变化规律。从图6 中可以看出随着热流密度的增加,液相表观速度先增大后减少,存在一个最佳热流密度使液相表观速度达到最大值。并且发现随着管径的增大,最佳热流密度的值也在不断的增大。这是由于当工质进入气泡泵中,吸收热量迅速气化,生成的气泡在浮力作用下向上运动。管径的增大会导致总质量流量的增大,单位时间内进入管内的工质变多,因此需要更大的热量才能让其气化。随着管径的增大,所能承受的热流密度值再不断增加,使液相速度最大的最佳热流密度值也就随之不断增大。
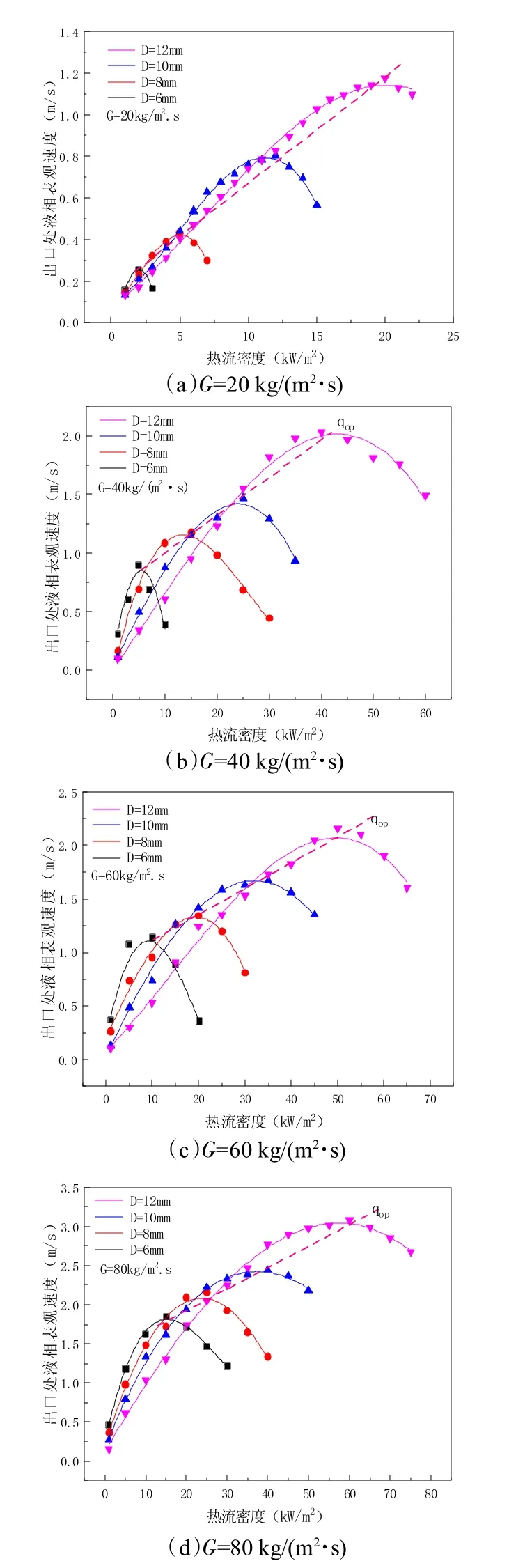
图6 不同加热量下出口处液相表观速度随管径的变化
4.2 泵送比分析
图7 为相同工况下泵送比与热流密度的关系图。泵送比是液相速度与气相速度的比值,可以用来表示单位蒸汽量能够提升液体量的大小[6],从而可以用泵送比来直观反应气泡泵提升能力的大小。整体来看,泵送比随着热流密度的增加先增大后减小,与出口液相表观速度变化相似且对于同一管径来说,出口最大表观速度对应的热流密度同时也是泵送比最大值所对应的的热流密度。随着管径的增大,泵送比最大值反而随之减小。与 Soo W.Jo[6]结论相同。

图7 泵送比随热流密度的变化
泵送比的提升是由于热流密度的增加或者半径的减小,因为更大的热流会带来更大的浮力。当热量开始输入时,气泡泵中不断有气泡生成,且随着热量不断增加,气液两相速度趋于一致,此时泵送比达到最大。而随着热流密度继续变大,液相只能贴附在气泡泵管壁流动从而速度降低,气体则会形成气柱,气相速度继续增大,泵送比则会减小,不能更好的提升流体。增加热量的输入会产生更大浮力,也会进一步加速提升液体。气泡泵直径增加,具有更大半径长度比的气泡泵由于半径方向上热阻的增加,反而削弱传热效率。
4.3 滑速比分析
滑速比即气相和液相速度的比值,滑速比与泵送比互为倒数,当滑速比接近为1 时,气泡泵提升能力最大。在以上研究基础上,选取管径D=6 mm,进口流量G=40 kg/(m2·s)下的气泡泵进行模拟,在同一管径下,随着轴向高度的增大,滑速比反而下降(图8)。从而可得,随着轴向高度的增加,气相速度与液相速度逐渐一致。对比不同热流密度,随着热流密度的增大,滑速比反而减小,且气泡泵从进口到出口的滑速比减小速率增大。所以增加加热量,滑速比随之减小,即气泡泵提升性能越好[6]。在同一热流密度下,滑速比沿轴向方向逐渐减小,当热流密度为5 kW/m2和6 kW/m2时,出口滑速比近似于1。此时气相速度与液相速度基本相等,气泡泵此时提升性能达到最佳。可以根据滑速比设计气泡泵提升管的长度,当气泡泵提升管直径为6 mm。滑速比为1.2 时,对于6 kW/m2的热流密度,气泡泵提升管最佳长度为0.5 m,而对于5 kW/m2的热流密度气泡泵提升管最佳长度则为0.75 m。
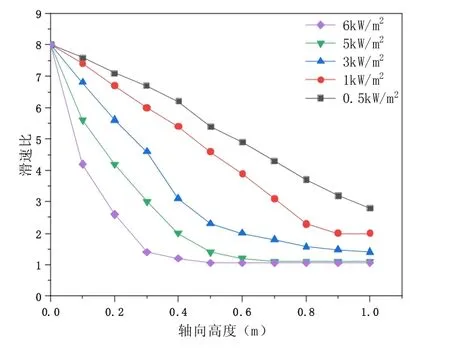
图8 滑速比沿轴向方向的分布
4.4 空泡份额分析
截面平均空泡份额作为流态转变参考值从而可以识别流态,泡状流,弹状流,搅拌流和环状流转变为空泡份额参考值分别为0.3、0.55、0.8[13,14]。图9 为以D=6 mm 为例,轴向方向上截面平均空泡份额的分布情况。可以看出随轴向高度的增加,空泡份额持续增加,且增加幅度逐渐放缓。随着热流密度的增加,相同高度的轴向截面空泡份额呈逐渐增大的趋势。在整个轴向的变化过程中,0 m 到0.1 m 的增长幅度最为迅速,而之后空泡份额的增加幅度逐渐放缓,这是由于当饱和水在1atm 下进入气泡泵时,有热量输入,将迅速达到过热状态,随着热量的持续加入,气泡不断的产生、脱离,从而使管内的空泡份额急剧增加。气泡碰撞频次随着热量不断地输入而增加,小气泡聚合成弹状大气泡。管壁与管中心液体被气泡隔离开,管壁热量输入被气泡阻隔,难以加热管中心液体[15]。所以在进口段外空泡份额增加速度变缓。

图9 空泡份额沿轴向的分布
根据图8 可知,在D=6 mm 时,泵送比在热流密度为5 kW/m2时达到了最大值,而根据图9 显示的结果,在热流密度为5 kW/m2时管内以搅拌流为主。当热流密度为1 kW/m2时,管内出口处的流态是弹状流,但泵送比却高于10 kW/m2时所对应的环状流。这说明不同流态对泵送比有显著影响,根据此次研究的结果,可以发现就提升能力而言,搅拌流 >弹状流 >环状流。这是因为环状流时会形成连续的气柱,液相被气柱挤压到管壁上,此时液体很难依靠气柱的浮力向上运行,因此随着热流密度的增加,提升能力反而下降[4-5]。
如图10,当q=10 kw/m2时,模拟不同管径相同热流密度对空泡份额的影响。整体来看,随轴向高度的增加,空泡份额持续增加,且增加幅度逐渐放缓。热流密度相同时,空泡份额随着管径的增加反而减小。当在q=10 kw/m2时,管径为6 mm 的提升管内部大部分已经达到环状流,而管径为12 mm 的提升管管内流态大部分为泡状流和弹状流。管径的增大会导致质量流量的增大,单位时间内进入管内的工质变多,所以需要更多的热量才能让其气化。
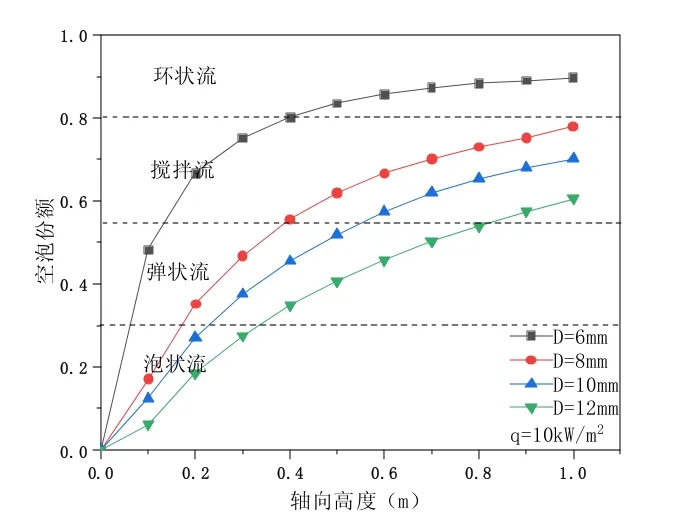
图10 q=10 kW/m2不同管径截面平均空泡份额
4.5 沿程液相表观速度的变化规律
如图11,在进口质量流量G=40 kg/(m2s),管径D=6 mm 时,小加热功率(q=1、3、5 kW/m2)下,液相表观速度随高度的增加不断增大,近似线性增大。但是,在大加热功率((q=6、8、10 kW/m2)下,液相表观速度随高度的增加先增大到达最大值后减少,呈现抛物线变化趋势,且液相表观速度出现最大值所对应的轴向高度随着热流密度的增大而减小。

图11 液相表观速度沿轴向高度的变化
气泡泵内的流态发生变化是造成液相表观速度的减少的原因。在大加热功率下,液相表观速度随高度的增加呈现抛物线变化趋势,这是因为垂直管内有环状流出现。热流密度增大,气泡数量增加。热流密度过大,导致气泡泵内气泡数量急剧增加,管内流动扰动增强,虽然管内换热增强,但是由于流态发生变化,由提升能力较强的搅拌流、弹状流向环状流转变,液相表观速度降低,相应的液相提升量减少。热量不断输入,管内流态会随着热流密度的增大而不断变化,热流密度越大,越容易有环状流的出现从而导致液相表观速度降低。
4.6 最佳热流密度
最佳热流密度(qop)为提升液相最多时所对应的热流密度值。如图6 中的虚线,发现在图中将拟合后的抛物线的顶点进行连接,不同管径下的最佳热流密度值接近线性变化。改变图6 中的流量,发现出口液相表观速度的变化与图6 趋势相类似,即最佳热流密度与管径和进口质量流量都有关,为找到三者之间的关系,将不同管径的最佳热流密度点进行拟合,最终结果如图12 所示。

图12 不同进口流量下最佳热流密度随管径的变化
如图12 所示,相同进口质量流量G下,最佳热流密度与管径D的线性关系可以表示为:

根据图12 可以得到不同进口质量流量下所拟合直线信息,见表3。最佳热流密度与管径D成线性关系,而未知数斜率a和截距b的变化与进口质量流量G的大小有关。在每个质量流量下都存在一个最佳热流密度。
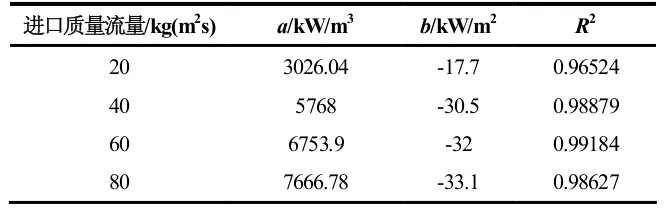
表3 a、b值和图5 拟合直线回归系数R2
不同的进口流量下拟合直线的斜率和截距不同,将数据进行拟合,如图13、14,得到拟合曲线表达式:
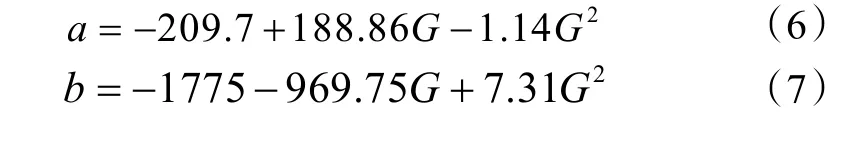

图13 a值随进口质量流量的变化拟合曲线

图14 b值随进口质量流量的变化拟合曲线
将式(6)和式(7)代入式(5)可得到最佳热流密度与进口质量流量和管径的关系式:
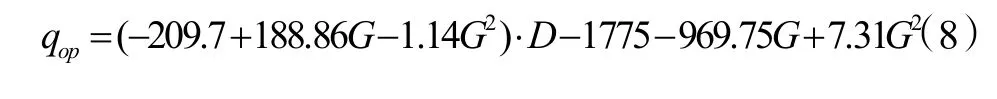
5 结论
本文利用两相流理论建立稳态气泡泵两流体模型,以1atm 下饱和水为工质,采用 CFX-19 模拟研究沿程加热气泡泵流动沸腾,本文主要研究结论如下:
1)出口处液相表观速度随热流密度的增大是先增大后减少,呈现抛物线变化,存在一个使得出口液相表观速度达到最大的最佳热流密度。
2)在同一管径下,滑速比沿着轴向方向逐渐减小,不同热流密度,随着热流密度的增大,滑速比反而减小,且气泡泵从进口到出口的滑速比减小速率增大。
3)泵送比随着热流密度的增加先增大后减小,与出口液相表观速度变化相似且对于同一管径来说,出口最大表观速度对应的热流密度同时也是泵送比最大值所对应的的热流密度。随着管径的增大,泵送比最大值反而随之减小。
4)在气泡泵轴向,截面平均空泡份额的变化趋势是先迅速增大,然后逐渐变缓。出口液相表观速度随热流密度的增大呈现抛物线变化,结合流态分析,得出最佳提升性能下的流态为搅拌流。
5)在小于最佳热流密度下液相速度在气泡泵轴向接近线性增加。热流输入大于最佳热流密度时,液相速度在轴向上的变化是先增大后减少,存在一个最大值,呈现抛物线趋势变化。
6)最佳热流密度与进口质量流量成二次函数关系,与管径成一次函数关系。
