管内扭带插入件强化沸腾换热技术的研究现状及展望

黄沈杰 熊 通 汪根法 刘 杰 徐占松 晏 刚

(1 西安交通大学能源与动力工程学院 西安 710049；2 浙江同星科技股份有限公司 新昌 312521；3 陕西重型汽车有限公司 西安 710043)

工业生产对紧凑高效换热系统的需求促使人们研究换热器的强化换热技术。传热强化技术可以分为主动强化、被动强化和复合强化3种[1]。主动强化需要外部能源提高传热速率，被动强化主要对换热器件的表面进行几何修改。扭带内插是一种历史悠久的强化换热技术，使用历史可追溯至1896年[2]。R. M. Manglik等[3]指出管内扭带插入件在蒸汽发生器、烟气热回收装置、家用加热器中都有应用；D.P.Shatto等[4]指出扭带在海水淡化装置中也有应用。

扭带插入物的制造简单、成本低[5]、便于安装和拆卸[1]，在相同的换热负荷下换热设备的体积更小，节省投资[6]。在制冷系统中，换热器尺寸的减小能够节省材料成本、减少制冷剂的灌注量和泄漏量[7]。扭带内插还能克服蒸发管中的局部干涸、管底沉油、沉垢等现象[8]。虽然对于紧凑型换热器而言，管外空气侧的传热热阻占据主导地位，但R.S.Reid等[9]研究证实，管内侧的传热强化也会导致整体传热系数的显著改善。因此，管内扭带插入件作为一种被动强化的换热技术受到很多学者的关注和研究。

图1所示为管内扭带插入件示意图，扭带的扭率被定义为扭带扭转180°的长度H与扭带宽度D之间的比值。通常情况下，扭带与管壁之间的间隙应尽可能地小。因为大间隙会产生旁通流，使扭带内插的性能下降[10]。

图1 管内扭带插入件示意图[11]Fig. 1 Twisted tape insert in the tube[11]

Varun等[10]就管内扭带插入件这一强化换热技术进行了综述，但并未专门就扭带在沸腾换热中的应用作出详细叙述；D.P.Shatto等[4]就管内扭带插入件在沸腾换热中的应用进行了综述，但该文章发表于1996年，未能涵盖之后的研究成果。本文将主要评述管内扭带插入件在沸腾换热中的应用，从原理、参数分析、评价方式、关联式等角度分析这些文献的研究成果，且能涵盖最近二十多年的研究成果，弥补了前人的不足。管内扭带插入件在制冷系统蒸发器中具备良好的应用潜力，能够使蒸发器向小型化、紧凑化发展，实现节能、节材的效果。因此，本文能够为扭带在制冷系统蒸发器中的应用提供一定的参考。

1 管内扭带插入件对沸腾换热产生强化作用的原理

扭带本质上是一种扰流原件。扭带内插入管中，将原本在管内流动的单股流体分成两股，迫使这两股流体按照扭带的形状旋转流动。

根据R. M. Manglik等[3]的观点，扭带在单相流中的强化换热原理主要体现在5个方面：

1)流动长度增加：扭带的插入能够使流体延长流动路径，从而使管内流体与外界的换热更加充分；

2)涡流效应：扭带的插入使流体沿管内轴向流动的速度矢量与沿着扭带形状流动所产生的速度矢量相叠加，产生涡旋流，破坏管壁的流动边界层；

3)翅片效应：扭带与管壁的紧密结合使外界的热量能够传递至扭带，使扭带充当了翅片的作用，扩展了管内流体与外界的传热面积；

4)水力直径减小：扭带的插入使管内流体被分成了两股水力直径较小的流体，增大了湿周；

5)截面堵塞：扭带的插入使垂直于流动方向的管内横截面积缩小，在流体的质量流量一定的条件下，流体的流速增大。

而在沸腾换热这一两相流的条件下，管内扭带插入件能够强化换热的原理还有很多。

扭带的插入能够使流型从分层流提早转变为环状流，使管内工质与管壁的接触面变大，达到强化换热的效果[2,4,12]。K.N.Agrawal等[13]也指出扭带插入引起的离心力使液相工质向壁面移动，而气相位于管子中间流动，有助于流型转变为环型流。

M.A.Akhavan-Behabadi等[14]指出扭带插入到蒸发器的末端能够推迟蒸干现象的发生。A.E.Bergles等[15]指出涡流发生器在雾状流条件下能够促使液滴在壁面上沉积，增加润湿表面的长度；基于该结论，M.K.Jensen[16]建议在高干度区使用扭带。M.A.Kedzierski等[17]观察到扭带的插入能使壁面的局部蒸干面积增大，但同时在高干度区，扭带对液滴沉降的促进作用又能延迟完全蒸干现象的发生。

T.S.Mogaji[18]指出，扭带的旋流作用能够充分混合制冷剂和制冷系统中的润滑油，使润滑油避免聚集在壁面上，降低传热热阻；扭带的扰动也能使R407C等共沸制冷剂中的组分充分混合。D.P.Shatto等[4]指出在加热条件下流动的流体，扭带给予流体的向心加速度能够使密度较高的较冷流体移动至外围，取代较低密度的较热流体。

2 扭带强化沸腾换热的实验研究

大部分学者采用在管壁外侧贴电加热片的方式研究管内扭带插入件强化沸腾换热的效果。该方式简单易行，便于对沸腾换热的外界热流密度掌握和调节。学者们采用的测试对象均为一根单管，目前还没有学者对管内扭带插入件在整个蒸发器中的换热强化性能进行研究。表1所示为各学者的实验参数汇总。

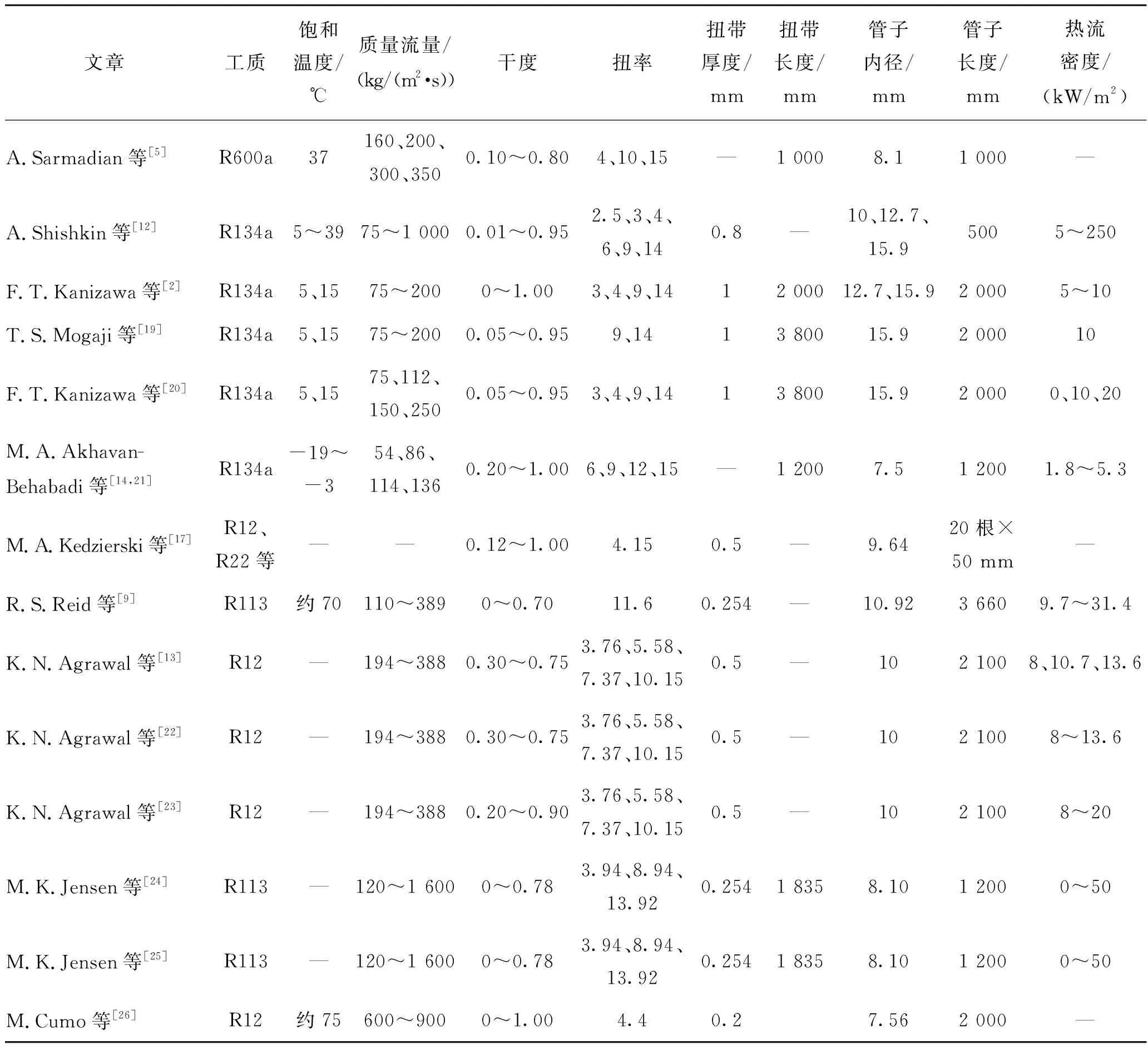
表1 扭带强化沸腾换热的实验数据汇总Tab. 1 Summary of experimental data of twisted tape insert to enhance boiling heat transfer

3 扭带内插效果的影响因素分析

任何强化换热的技术都是一把双刃剑，在起到强化换热效果的同时，也会给系统压降带来负面影响，管内扭带插入件也不例外。所以，表面传热系数和压降是学者在扭带内插效果中主要关注的因变量，只关注扭带内插带来的换热增益是片面的。在制冷系统中，压降过大会导致压缩机功耗增大，给制冷系统的整体性能带来不利影响。但D.P.Shatto等[4]指出可以通过减小换热器尺寸来克服由扭带插入引起的换热器压降增大。参数方面，扭带的扭率、内插管的管径等结构参数和工质的质量流量、干度、在管内沸腾的饱和温度等流动参数是学者研究的主要自变量。

扭率是所有研究扭带内插的学者普遍研究的一个重要参数，正如图1所示，它代表了扭带的扭曲程度。通常而言，扭率越小，即扭带的扭曲程度越大，管内工质被扰动得越剧烈、与管壁的接触越充分，工质与管壁的传热系数越大、管内的压降也越大。F.T.Kanizawa等[20]和K.N.Agrawal等[23]均指出，随着扭率的增大，两个扭率之间的压降梯度(指单位管长的管内压降)之差会减少。但也有一些例外情况，F.T.Kanizawa等[2]和T.S.Mogaji等[19]均观察到当质量流量较小时，管内工质的流动处于层流状态，若扭带的扭率又较大，对工质的扰动作用微弱，则扭率大小对换热效果几乎没有影响。

扭带内插管管径的大小也会影响换热效果和压降。一般而言，管径越小，表面传热系数和管内压降越大。在管内质量流量一定的条件下，管径越小意味着管内工质的流速越大，工质与管壁的换热越充分、产生的摩擦压降也越大。研究管径对于扭带内插管换热效果的学者较少，仅F.T.Kanizawa等[2]研究了12.7 mm和15.9 mm两种管径对于扭带内插效果的影响。可能是由于制冷空调领域通常使用的换热器管径较少，所以学者只研究一些固定型号的管径。

一般情况下，管内流动工质的质量流量与沸腾换热的表面传热系数及管内的压降均呈正相关。因为质量流量越大，工质的流速越大，越有利于沸腾换热过程中的对流沸腾，表面传热系数越大；质量流量越大，管内工质的沿程阻力损失和局部阻力损失也越大，管内的压降越大。例外情况仍然存在，A.Shishkin等[12]指出干度在质量流量对表面传热系数的影响程度中起到的作用，在低干度区，核态沸腾在沸腾换热中占主导作用，表面传热系数几乎不受质量流量大小的影响；而随着干度的增大，对流换热占主导地位，此时表面传热系数受质量流量的影响显著。

关于干度的研究也较多。一般情况下，沿着管内工质的流动方向，工质的干度会逐渐增大。而随着干度的增大，表面传热系数逐渐增大，直至管壁出现蒸干现象后，表面传热系数会急剧下降。但也有研究指出[2,18-19,27]，在低质量流量下，由于管内流动处于分层流状态，表面传热系数随干度的变化趋势不显著。此外，M.K.Jensen等[24，26]的实验数据也表明，在低干度区，核态沸腾效应占主导地位，管内扭带插入件在该条件下无法较好地发挥强化换热作用。当干度增大时，扭带内插管内的单位长度压降呈先上升后下降的趋势，其峰值一般出现在高干度区。F.T.Kanizawa等[2]指出，这与管内流型的变化有关。当管内流型由环状流转变为雾状流时，压降出现峰值。何燕[1]通过数值计算也发现了压降随干度的增大呈先增大后降低的趋势，当干度增大时，气液相的平均密度增大，在质量流量一定的条件下，工质的流速增大，从而使摩擦压降增大；而在雾状流区域，管壁出现干涸现象，此时液态工质不再以管壁上的液膜形式出现，而是以雾状液滴的形式存在，因此，摩擦压降显著下降。

饱和温度对压降和表面传热系数的影响也需要一分为二地看待。饱和温度一般与压降呈负相关。一方面，饱和温度降低会导致气相制冷剂的密度降低，在质量流量一定的条件下，其流速得到增大；另一方面，饱和温度降低也会引起液相黏度增大，导致压降增大。饱和温度与表面传热系数的关系不是十分明确，T.S.Mogaji[18]观察到较低的饱和温度能产生较高的表面传热系数，推测这是因为饱和温度的降低使气相流速增大，强化了换热效果，F.T.Kanizawa等[2]实验发现在15.9 mm管中，当质量流速较低且干度高于0.15时，也是饱和温度较低的工况拥有较高的表面传热系数；但在F.T.Kanizawa等[2]大部分的实验工况下，饱和温度的增加反而会导致表面传热系数增加。笔者推测，这是因为饱和温度的增加会导致管内流体与管外的平均传热温差减小，从而增大了表面传热系数。

4 扭带内插效果的评价方式及对应的扭带内插适用条件

管内扭带插入件作为一种强化换热方式，我们需要知道其达到最佳使用效果的结构条件和流动条件。

4.1 热力学第一定律评价方式

大部分学者采用热力学第一定律的评价方式，即从换热增益和压降惩罚的角度评价扭带内插的效果。

换热增益是指在相同的工况条件下，扭带内插管的局部表面传热系数与无扭带光滑管的局部表面传热系数之比，如式(1)所示。

(1)

式中：ht为扭带内插管的局部表面传热系数，W/(m2·K)；hs为无扭带光滑管的局部表面传热系数，W/(m2·K)；PF1为性能因子(performance factor)1，即换热增益。

压降惩罚是指在相同的工况条件下，扭带内插管的单位长度上的局部压力损失和无扭带光滑管的单位长度上的局部压力损失之比，如式(2)所示。

(2)

式中：Δpt为扭带内插管的局部压力损失，Pa；Δps为无扭带光滑管的局部压力损失，Pa；PF2为性能因子2，即压降惩罚。

也有一些学者[5]为了从换热和管内压降(或泵送功率)的角度综合考虑扭带内插的效果，提出了性能因子3，即综合性能PF3，其物理意义为换热增益与压降惩罚的比值，也可以理解为单位管内压降(或单位泵送功率)下的表面传热系数之比，如式(3)所示。但K.N.Agrawal等[13]指出在蒸气压缩制冷系统中，相对于泵送功率而言，采用管内压降作为对比对象更加合适。

(3)

学者们主要应用的热力学第一定律评价方式就是PF1、PF2和PF3。其余应用较少的评价方式不再一一列出。

通常情况下，PF1、PF2的值大于1，因为扭带的插入必定会增强换热、增大压降；而等泵功(或等压降)下的传热系数之比——PF3的值可能会大于1、也可能会小于1。学者们把PF3的值大于1作为扭带内插管优于无扭带内插管的判据[5]，即该情况下使用扭带内插技术是有利的。

4.2 热力学第二定律评价方式

此外，也有极个别学者从热力学第二定律的角度分析扭带内插的最优条件。S.G.Holagh等[11]从熵产的角度评析了管内扭带插入件的最佳适用条件。式(4)为单位管长上的熵增。式(5)为S.G.Holagh定义的熵产数。根据该作者的定义，当熵产数小于1时，即表征内插扭带管的性能优于无扭带光滑管[17]。

(4)

(5)

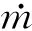
4.3 综合分析

表2汇总了各文献评价扭带内插性能的指标，以及由这些评价指标分别得出的评价结论。

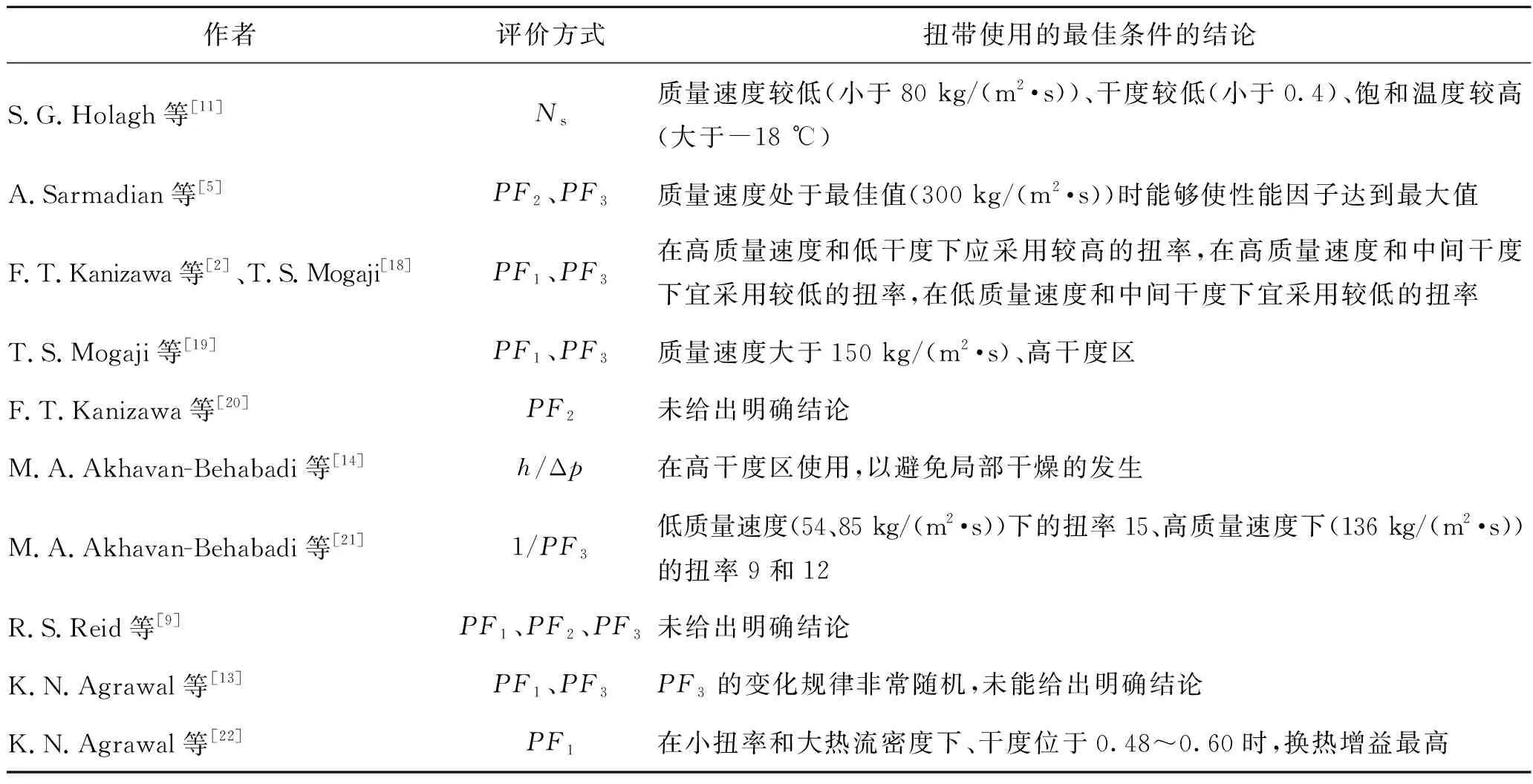
表2 扭带内插效果的评价方式与评价结论汇总Tab. 2 Summary of evaluation methods and evaluation conclusions of twisted tape insert

事实上，这些评价指标的运用没有适用工况范围的限制，只有学者使用的频次高低之别。在管内扭带插入件强化沸腾换热的研究领域，最受认可、最广泛应用的评价方式是表征综合性能的性能因子PF3。由表2可知，有60%的文献均应用了该评价方式。PF3得到广泛应用的原因可归结为两点：一方面，这一热力学第一定律的评价方式的推导过程简单、结果呈现方式也直观。相比之下，热力学第二定律的评价方式具有推导过程繁琐、获取数据复杂、物理意义不直接、结果表达不直观等缺点，因此在扭带内插强化沸腾换热的评价方法中应用得很少。目前，仅有S.G.Holagh等[11]在文献中应用了熵产的热力学第二定律的评价方式。另一方面，相比于其他热力学第一定律的评价方式，PF3的指标更加全面科学。PF1只考虑了扭带内插给换热带来的强化作用，忽视了这一技术给系统功耗带来的不利影响；类似地，PF2这一评价方式只表征了扭带内插带来的压降增大倍数，无法反映扭带内插这一强化换热技术的本质。而PF3兼顾了被动强化换热技术对换热效果产生的正面作用和对流动压降产生的负面作用，避免了PF1和PF2片面评价的缺点。

事实上，不止在扭带内插领域，在其他强化换热技术中，类似PF3以换热增益与压降惩罚的比值定义评价指标是一种非常通行的做法。这在文献[7,28-30]中均有所阐述。一种更普遍的做法是分别以努塞尔数和阻力系数代替式(3)中的表面传热系数和压降。在式(3)中，K.N.Agrawal等[13]指出应以PF3大于1作为扭带使用有益的判据。但通常情况下，扭带内插引起的压降的扩大倍数远大于其引起的换热增益的倍数，如在A.Sarmadian等[5]的实验中，PF3在0.44～1.09之间，绝大多数工况条件下PF3均在1以下。因此，该条件过于苛刻，使用PF3作为判据不尽合理、对工程实际的指导意义较小。而一种较为合理的扭带内插效果的评价方式是适当减小压降惩罚的影响。文献[28,30]均论述了努塞尔数之比与阻力系数之比的三分之一次幂作为评价指标的合理性，因此，在后续研究中可采用类似的思路，适当缩小式(3)中压降之比的指数。

目前为止，在各种评价方式下，各学者得出的扭带最佳适用条件的结论十分不统一，甚至会相互矛盾。原因可归纳为以下三点：

1)沸腾换热是一种非常不稳定的、完全湍流的两相流过程，并且扭带的插入又增加了湍流现象，使流动条件更加复杂[5]。流动条件的复杂性决定了实验结果的不唯一性和不确定性。

2)不同的评价指标也会使研究者得出不同的扭带最佳使用条件的结论。例如，就干度这一参数而言，S.G.Holagh等[11]的数值计算结果证实了较低的干度(小于0.4)是扭带使用的最佳条件之一，此时内插扭带管的熵产小于无扭带平直管的熵产；K.N.Agrawal等[22]的结论指出扭带在中等干度区(0.48～0.6)使用最佳，此时换热增益PF1最大；M.A.Akhavan-Behabadi等[14]和T.S.Mogaji等[19]均认为扭带在高干度区使用最佳，理由分别为能够防止局部干燥的发生和综合性能因子PF3最高。

3)各实验工况在数量上的有限性也导致各学者得出的结论对于实验工况的高度依赖性。换言之，限于实验条件，对于影响扭带内插效果的大多数变量而言，学者们无法研究该变量在不间断连续变化条件下对扭带内插性能的影响，只能将各变量以离散化的方式进行实验研究。很多情况下，对质量流量等变量而言，学者选取的离散程度较大或选取的离散变量的变化范围较小。因此，各学者总结出的各变量对扭带内插管性能的变化规律及对应的扭带内插最佳适用条件高度依赖于选取的实验工况。单个学者的结论难以避免因实验工况受限而造成的片面性和不完整性，而多个学者分别得出的结论则难以避免互相不统一、甚至相互矛盾的情形。

5 扭带内插强化沸腾换热的关联式

5.1 表面传热系数关联式

目前为止，学者们拟合内插扭带管表面传热系数关联式的方法可分为三类：双面兼顾法、换热增益法、直接拟合法。

1)双面兼顾法

扭带对两相沸腾管内流体的扰动作用和对壁面流体边界层的破坏作用一方面抑制了核态沸腾下汽化核心的生长和成型，另一方面又加大了对流换热强度。因此，“双面兼顾法”通过选取合适的核态沸腾抑制因子和对流沸腾增强因子，再分别把这两个因子与学者选取的液态对流换热表面传热系数关联式和核态池沸腾的表面传热系数关联式进行乘数叠加，并引入渐近指数n，最后得到内插扭带管内沸腾换热的表面传热系数。“双面兼顾法”的通用计算式如下：

ht=[(hnbS)n+(hcF)n]1/n

(6)

式中：ht为内插扭带管内沸腾换热的表面传热系数，W/(m2·K)；hnb为核态池沸腾换热的表面传热系数，W/(m2·K)；hc为液态对流换热的表面传热系数，W/(m2·K)；S为核态沸腾抑制因子；F为对流沸腾增强因子。

在预测内插扭带管沸腾换热的表面传热系数关联式时主要应用双面兼顾法的学者有M.K.Jensen等[24]、F.T.Kanizawa等[6]、A.Shishkin等[12]。

第一位是M.K.Jensen，M.K.Jensen等[24]以J. C. Chen[31]的模型为基础加以修正，得到关联式(7)～式(12)。式(10)和式(11)分别为不同学者给出的关于对流沸腾增强因子F的两种预测式，M.K.Jensen认为采用任意一种都能获得合理的预测结果。何燕[1]文章中关于M.K.Jensen换热关联式的引用存在错误之处在于保留了式(7)中的单相轴流表面传热系数hl，而没有依据M.K.Jensen文中的原意将其替换为扭带内插入单相流的表面传热系数hc。

ht=hnbS+hcF

(7)

(8)

(9)

(10)

F=[(dp/dz)t/(dp/dz)s]0.444

(11)

S=(kl/hlFX0)(1-e-hlFX0/kl)

霍译：Almost without thinking where she was going,she made her way to the House of Green Delights.

(12)

式中：kl为管内液体的导热系数，W/(m·K)；Dh为水力直径，m；Re为雷诺数；Pr为普朗特数；cp,l为液体的比热，J/(kg·K)；ρl为液体密度，kg/m3；σ为表面张力，N/m；μl为液体的动力黏度，kg/(m·s)；hfg为汽化潜热，J/kg；ρg为气体密度，kg/m3；ΔT为壁面温度与工质饱和温度之差，K；Δp为ΔT引起的蒸气压力之差，Pa；hl为管内液体与外界的表面传热系数，W/(m2·K)；Fe为表征翅片效应的参数，具体取值见文献[6]；α、χ、X0分别为一些中间变量，计算方式见文献[24]。

第二位是F.T.Kanizawa，F.T.Kanizawa等[6]基于管内流型提出了预测内插扭带水平管流动沸腾的表面传热系数模型。将流动分为3个区域：流动沸腾区(干度低于蒸干开始时期的干度)、蒸干区(从蒸干开始至蒸干结束)和雾状流区(干度高于蒸干完成时的干度)，在这3个区域分别预测关联式。F.T.Kanizawa在流动沸腾区采用的预测方法即双面兼顾法，在蒸干区和雾状流区，在L.Wojtan等[33]提出的平直管沸腾换热的表面传热系数关联式的基础上直接改进。

在流动沸腾区，基于Liu Z.等[32]提出的无扭带平直管内的表面传热系数关联式，并结合扭带产生的旋流对核态沸腾的抑制作用和对对流换热的增强效应，F.T.Kanizawa提出了表面传热系数关联式(13)。

ht=[(hnbS)2+(hcF)2]1/2

(13)

式中hc计算式参考式(8)，hnb计算式如式(14)所示：

(14)

式中：φ为热流密度，W/m2；m为一与pr有关的中间变量，计算方式见文献[6]；fw为与表面材料有关的无量纲数[6]；pr为对比压力；Ra为表面粗糙度，μm；M为摩尔质量，kg/kmol。

而对流增强因子和核态沸腾抑制因子分别为：

(15)

(16)

式中：Prl为管内液相工质的普朗特数；Π2为文献[6]定义的表征管径大小的无量纲数；x为干度；Rel0为液态形式混合流的雷诺数。

(17)

(18)

(19)

式中：hmist为雾状流区的表面传热系数，W/(m2·K)；Prg为气态工质的普朗特数；kg为管内气体的导热系数，W/(m·K)；d为管子内径，m；G为管内工质的质量速度，kg/(m2·s)；μg为气体的动力黏度，kg/(m·s)。

而在中间的蒸干区，F.T.Kanizawa仍以L.Wojtan等[33]的无扭带直管的雾状流区域的关联式为基础，得到如下关联式：

(20)

式中：hdryout为蒸干区的表面传热系数，W/(m2·K)；ht为式(13)的两相区表面传热系数，W/(m2·K)；xdi、xde分别为蒸干区起始、结束的干度。

第三位是A.Shishkin，A.Shishkin等[12]指出F.T.Kanizawa等[6]提出的关联式适用于中等或较低的质量流量和热流密度，但与高质量流量和高热流密度下的实验数据不相符。同样地，采用双面兼顾法，A.Shishkin将表面传热系数ht视为核态沸腾与强迫对流换热叠加的结果，提出了在高热流密度(q≥100 kW/m2)和高质量流量(G≥400 kg/(m2·s))下的表面传热系数关联式(21)～式(25)。

ht=[(hnbS)3+(hcF)3]1/3

(21)

(22)

(23)

S=1.0

(24)

(25)

式中：Nunb为核态沸腾的努塞尔数；Re*为气泡混合雷诺数，定义方式见文献[12]；y为扭率；Kp为无量纲数，表征压力与表面张力的联系，定义方式见文献[12]；Nuc为对流换热的努塞尔数；t为扭带的厚度，m。

2)换热增益法

换热增益法即通过实验数据观察影响内插扭带管与无扭带平直管的表面传热系数之比的物理因素，引入一些无量纲数将这些因素参数化，通过实验数据拟合出表征换热增益与各参数的函数关系的关联式。目前，只有K.N.Agrawal等[22]应用了该方法。

K.N.Agrawal通过实验分析得出换热增益主要取决于扭率、热流密度和质量流量等3个参数，并认为扭带内插引起的换热增益是通过强制对流效应和旋流效应体现的。通过引入两个无量纲数——沸腾数Bo、雷诺数Re来体现强制对流效应，引入扭率y来体现旋流效应。K.N.Agrawal给出了预测精度十分近似的两个关联式，即式(26)和式(27)。两个关联式推导过程的区别是式(26)是纯粹的经验关联式，式(27)的推导过程充分考虑了旋流作用的物理表达，并分开考虑了此类流动中存在的螺旋对流效应和离心对流效应。

(26)

(27)

3)直接拟合法

直接拟合法的方法与步骤和换热增益法的类似。学者们通过文献调研、实验观察等方法确定对内插扭带管沸腾换热的表面传热系数有主要影响的物理量，将这些参数无量纲化以确保关联式对不同实验工况的可推广性，再通过实验数据拟合的方式确定关联式中的各项系数，得到旋流状态下的努塞尔数与各物理量的函数关系式。常被选用的无量纲数有雷诺数Re、沸腾数Bo、普朗特数Pr、韦伯数We等。运用直接拟合法的学者有M.A.Kedzierski等[17]和何燕[1]。

M.A.Kedzierski等[17]以R12、R22、R152a、R134a、R290、R290/R134a(44/56)、R134a/R600a(81/19)等7种制冷剂的实验数据为基础，拟合出如下努塞尔数关联式：

α1=0.993-1.181x+0.899x2

α2=1.108-2.366x+1.451x2

α3=-2.383+5.255x-1.791x2

α4=-3.195+6.668x

α5=1.073-2.679x+1.443x2

(28)

式中：Nup为纯质或共沸工质的努塞尔数；Sw为旋流参数，定义方式见文献[17]。

而对于R32/R152a和R32/R134a两种非共沸混合制冷剂，M.A.Kedzierski等考虑了每种非共沸混合制冷剂的露点温度和泡点温度之差Td-Tb以及每种非共沸混合制冷剂中的两种组分的饱和温度之差TLV-TMV，引入了无量纲数Θ，定义为：

(29)

得出的努塞尔数关联式为：

α1=-0.58+5.67x-2.825x2

α2=-2.793x

α3=1.204-3.335x+1.946x2

α4=0.338+0.353x

α5=0.839

(30)

式中：Num为非共沸混合制冷剂的努塞尔数；xg为气体的摩尔分数；xl为液体的摩尔分数。

此外，何燕[1]从F.T.Kanizawa等[2]、T.S.Mogaji等[19,27]、K.N.Agrawal等[22]、R.S.Reid等[9]的文献中提取表面传热系数的实验数据，拟合出了努塞尔数的关联式：

(31)

式中：Rel为液态工质的雷诺数；MH2为氢气的摩尔质量，kg/kmol；Welo为假设全为液态工质所计算得出的韦伯数。

5.2 压降关联式

内插扭带管沸腾换热的压降预测关联式以扭率倒数法为主，而其余非应用该方法的关联式基本也是在扭率倒数法的基础上进行合理变形后得出的。

1)扭率倒数法

扭率倒数法的模型最简单、接受程度最广、应用也最广泛。研究者们通过实验发现，当扭带插入两相沸腾的管中时，压降会随之增大，且压降的增幅与插入扭带的扭率呈反比。用扭率倒数法预测关联式的步骤如下：学者以无扭带平直管中的沸腾换热的压降关联式为基础，并根据学者自己的内插扭带管管内沸腾压降的实验数据，计算出在相同工况条件下的内插扭带管中的压降数值与无扭带平直管中的压降数值的比值。最后，再以式(32)的形式，拟合出C和n的数值，得到表征内插扭带管内的沸腾压降与无扭带平直管内的沸腾压降的比值和扭带扭率的函数关系式。

(32)

式中：Δpt为内插扭带管内的沸腾压降，Pa；Δps为无扭带平直管内的沸腾压降,Pa。

应用扭率倒数法的学者有T.A.Blatt等[34]、K.N.Agrawal等[23]、M.K.Jensen等[25]、和M.A.Akhavan-Behabadi等[14]。

T.A.Blatt等[34]以R12的旋流实验数据为基础，拟合出如下关联式：

(33)

K.N.Agrawal等[23]结合R. C. Martinelli等[35]提出的平直管内的沸腾压降关联式，拟合实验数据，得到关联式(34)。

(34)

M.K.Jensen等[25]在选用的无扭带平直管内压降关联式的基础上，为小扭率条件下的内插扭带管的压降预测和大扭率条件下的压降预测分别选用了不同的关联式，以使内插扭带管中的摩擦因子与无扭带平直管中的摩擦因子之比恒大于1。两个关联式适用扭率的分界点为11.25。

(35)

式中：ft、fs分别为内插扭带管和无扭带平直管中的摩擦因子。

M.A.Akhavan-Behabadi等[14]以L. Friedel[36]描述的平直管中的两相流的压降为基础，结合其本人实验所得的压降数据，得到关联式(36)。

(36)

2)其他方法

相比于扭率倒数法，其他关联式的预测方法除了保留扭率这一重要参数外，还添加了弗劳德数Fr、干度x以及其他流体物性参数，以使学者预测的该关联式更加契合其实验数据。

F.T.Kanizawa等[37]收集了文献中R134a的沸腾换热和空气、水的单相流动的实验数据，并通过引入弗劳德数体现重力和惯性力的作用，得到内插扭带管与无扭带管之间的摩擦因子的比值的关联式。

(37)

F.T.Kanizawa等[20]根据实验结果，将扭带内插管分成两个区域来预测压降。在第一个区域中，液体惯性力和重力相平衡，使流型呈现出停滞流、分层流和间歇流等形态。在第二个区域中，轴向动量和离心加速度迫使密度较高的液相工质移至管壁，使该区域的流型以间歇流、环形分层流和环形流为主。将两个区域的压降予以加和后，得到关联式(38)。

(38)

式中：Frl为液体工质的弗劳德数；Π为表征轴向惯性力与径向惯性力比值的无量纲数，定义方式见文献[20]。

何燕[1]从F.T.Kanizawa等[2,20]、M.A.Akhavan-Behabadi[14]、T.S.Mogaji等[19]公开发表的内插扭带管内流动沸腾的文献中提取了摩擦压降的实验数据，并根据这些数据修正了F.T.Kanizawa等[20]的模型，提出了压降关联式(39)。

(39)

6 总结

管内扭带插入件是一种廉价的、易于制造的强化换热技术，能够使制冷设备中的蒸发器提高传热效率，有利于换热器向小型化和紧凑化的方向改进，便于企业节约生产成本。本文归纳总结了现有的国内外文献对管内扭带插入件这一被动强化换热技术在两相沸腾换热中的研究，得到如下结论：

1)传热强化原理剖析

管内扭带插入件的强化换热原理有很多，如流动长度增加、涡流效应、翅片效应、水力直径减小、截面堵塞。在沸腾换热的两相流中，扭带具有促使流型转变为环型流、延迟完全蒸干现象的发生、避免使润滑油聚集在壁面上等能够达到强化换热效果的作用。

2)性能影响因素分析

影响内插扭带管强化换热性能的参数可以分为管径、扭率等结构参数和质量流量、干度、饱和温度等流动参数。通常而言，质量流量、干度的变化与表面传热系数和压降的变化呈正相关；而管径、扭率、饱和温度的变化与表面传热系数和压降的变化呈负相关。

3)扭带评价指标归纳

扭带的使用能够增大管内侧的表面传热系数，但也会使管内压降增大。目前，扭带内插效果的评价方式主要有从换热、压降角度考虑的热力学第一定律的评价方式和从熵产角度考虑的热力学第二定律的评价方式。单位管内压降(或单位泵送功率)下的表面传热系数之比是应用最多的评价指标。

虽然管内扭带插入件这一强化换热技术已经取得了一些初步的研究成果，但仍存在一些值得进一步研究的问题：

1)最佳使用结论不一，有待后续研究

沸腾换热是一种带有相变过程的两相流，扭带的插入又增加了湍流现象的发生，且各学者的实验工况条件有限、选取的评价指标不一，因此，目前人们得出的关于扭带使用的最佳条件的结论很不统一、甚至相互矛盾。扭带使用的最佳干度、最佳扭率、最佳质量流量仍不够明确，有待进一步研究。

2)实验装置较为单一，需要整机实验

目前，管内扭带插入件强化换热的实验研究对象均为单根直管，还没有学者在完整的翅片管换热器或完整的制冷装置上研究扭带插入带来的换热强化作用或给制冷装置性能带来的提升效果。此外，考虑到变频压缩机在制冷系统中日益广泛应用，在该变流量、多工况的条件下，扭带在换热器内插入的最优长度、最优数量、最优扭率还有待后续探索。

3)实验管径较为传统，有待与时俱进

近年来，针对一些新型环保制冷剂，制冷学界和产业界兴起了在换热器上使用3、5 mm等小管径换热器的趋势，而目前为止，学者研究的扭带内插管的直径大多为10、12.7、15.9 mm等较大管径。因此，有必要在小管径换热管(或整个小管径蒸发器)内开展管内扭带插入件强化沸腾换热的探索。