地铁列车协同操纵的节能优化方法

黄德青，蔡汉林，王青元，江 明，金 波，崔佳诺

（1.西南交通大学 电气工程学院，四川 成都 610031；2.西南交通大学 唐山研究生院，河北 唐山 063000；3.北京全路通信信号研究设计院集团有限公司，北京 100070）

截至2020年底，我国城市轨道交通全年总牵引能耗高达84亿kW·h，由于地铁占城轨交通运营总线路长度的78.8%，且承担了大城市主要公共交通运输任务，是城市轨道交通中的耗能大户[1]。因此，降低地铁系统总运行能耗对节能、环保以及践行国家的“双碳”政策都有着非常实际的意义。

列车牵引时会从牵引网吸收能量，电制动时则会向牵引网回馈再生能。通过列车间牵引过程和制动过程的重叠，可实现再生能的回收利用。目前，实现地铁列车协同操纵节能运行的研究主要包括优化列车操纵策略、优化时刻表[2−3]以及建立一体化节能优化模型[4]或2阶段优化模型[5−6]，对列车操纵策略和时刻表一并优化。由于对列车时刻表的改动可能会影响地铁系统的正常运营，调整时刻表的方法有其局限性。因此，诸多学者在不调整时刻表的前提下对列车协同操纵节能优化问题开展了一系列研究。文献[7]研究了2列列车协同运行控制方法，在前车采取4阶段运行策略（最大牵引-巡航-惰行-最大制动）的情形下，后车根据前车制动时间采取4阶段运行策略或5阶段运行策略（最大牵引-巡航/惰行-最大牵引-惰行-最大制动）来吸收前车产生的再生能。文献[8]在定时约束下，以前行列车和追踪列车总运行能耗为目标，利用遗传算法对2列列车操纵策略进行求解，实现了2列列车协同运行。文献[9]提出1种在线的列车协同控制方法，通过地铁控制中心实时地计算剩余再生能并进行分配，分配到再生能的列车通过增加1个牵引阶段对再生能进行吸收；由于再生能分配函数难以获得，该方法有一定的实现难度。文献[10]提出了1种根据变电站潮流，在最大能力曲线中加入惰行工况和最大牵引工况的列车运行曲线优化方法，该方法计算时间较短且能够降低变电站能耗。文献[11]提出了1种同供电区段下的实时协同控制模型，以4阶段运行策略为基础，在列车停站时利用协同进化算法同时优化多列车的运行曲线，但在考虑同一运行方向3列列车的情景下，该方法求解时间相对于实时计算的要求仍有不足。文献[12]基于滚动优化思想，实时地对单列列车的操纵策略进行优化，并依据其余列车的制动过程，在改进的4阶段运行策略基础上适当地增加1次牵引工况来提升再生能利用率，该方法具有较快的求解速度，但没有考虑整个供电区段的节能效果。

在既有时刻表的约束下，通过优化单车操纵策略实现多车协同操纵节能运行的研究仍较少，并且存在以下问题：（1）现有研究所取得的节能效果都是基于局部节能而言，没有考虑全局的优化效果；（2）大多数研究往往只考虑列车与其他1列或2列列车进行启发式地协同，没有考虑多列列车制动的情形和再生能的最优利用。

本文旨在通过优化各列车部分运行区间的操纵策略以提高再生能的利用效果，进而降低总运行能耗。基于分解思想，将列车群协同操纵全局优化问题转化为多车环境下的单车节能操纵优化问题；并在此基础上，设计1种在非均匀离散三维状态空间内寻优的动态规划算法对列车操纵策略进行求解，使得列车能够根据实际线路条件和可吸收再生能的时间分布最大程度利用再生能。

1 优化思想与假设

通过优化各列车操纵策略，可提升再生能利用率，降低总运行能耗。由于将全局所有列车操纵策略作为1个整体进行优化会导致模型复杂、求解困难，基于分解思想，可将优化问题转化为多个子问题[3]，即在一定时间内将1列或多列列车作为1个子系统，对子系统内列车的操纵策略进行优化，从而实现协同操纵。则全局总运行能耗Eglob可以转化为由多个子系统总运行能耗Esy1，Esy2，…，EsyN叠加组成，即：Eglob=Esy1+Esy2+…+EsyN，N为子系统个数。优化每个子系统总运行能耗，即可降低全局总运行能耗。

因此，下文在微观层面上以降低运行能耗为目标，利用列车运行过程中的外部功率表征其他列车的影响，对列车所在区间的操纵策略进行优化（如图1所示），以增大整体的再生能利用效果，并降低总运行能耗；在宏观层面上，根据一种运行图时域等效切分规则，缩小优化时间范围，并结合供电区段内未利用再生能的时间分布特征，选定各列车应优化操纵策略的区间，从而得到微观层次的优化对象。

为了简化研究问题，本文作出如下假设。

（1）回馈到牵引网的再生能只被同一供电区段内的列车吸收，不考虑其他供电区段的影响。

（2）由于牵引网阻抗非常小，忽略牵引网上的阻抗和电能损失[11]。

（3）不考虑储能设施，多余的再生能以热能形式散失。

2 基于多车环境的单车优化方法

2.1 优化模型

考虑到安全因素，只有发车间隔时间Th满足Th＞T−Tmin+tb时（tb为列车由线路最高限速停车制动时的制动时长，Tmin为区间最小运行时间），才对列车操纵策略进行优化。该约束是在前车准点运行，后车最大能力运行时的极端情况下给出的。由于地铁列车限速较低，区间运行时分短，一般来说该约束极易满足。

2.2 求解算法

本文模型适合利用动态规划算法在位置-速度-时间三维状态空间内求解，但由于“维数灾难”的问题，动态规划在三维状态空间内寻优时需要耗费大量计算的时间。基于文献[13—14]分别给出的在位置-速度二维空间上搜索的快速动态规划算法，设计1种在非均匀离散三维状态空间内寻优的动态规划算法，能够加快运算速度并获得优质解。

1）确定搜索状态

以线路中部位置离散间隔大于线路两端位置离散间隔的离散方式将线路非均匀离散为K个子区间（避免控制力频繁切换），并将第k个子区间终点位置xk作为第k个决策阶段（k=1，2，…，K）；以相同速度离散间隔Δv均匀离散速度，得到I个速度等级，则第i个速度等级的列车速度v=iΔv（i=0，1，…，I）。位置-速度空间离散形成网格，位置点xk与速度等级i构成网格上节点状态φ(k，i)。因而，列车在发车时刻t0的状态为φ(0，0)，到站时刻t0+T的状态为φ(K，0)。为了确定列车实际可达的节点状态，利用最大能力曲线限定列车在不同位置处的最大速度等级，进一步排除列车运行过程受实际约束而不可达的节点状态，如图2所示。

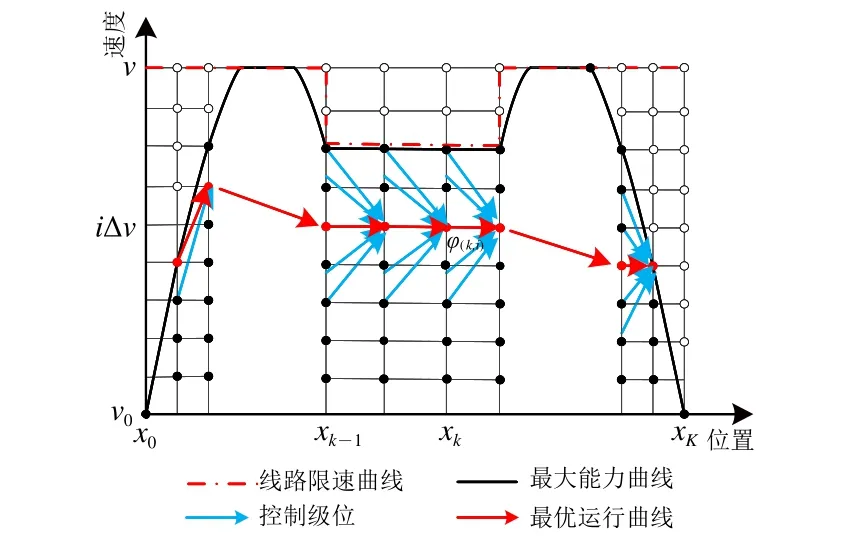
图2 动态规划状态转移示意图

2）单步状态转移

前向动态规划算法从第1阶段开始，求解至第K阶段，从而得到由φ(0，0)转移至φ(K，0)的最优操纵策略（即最优控制变量序列）。

为了减小动态规划算法计算量，采取遍历控制[15]的方式，将控制变量u∈[−1，1]均匀离散得到多个控制级位，从而使得列车能够进行最大牵引、部分牵引、惰行、部分制动和最大制动等多种运行工况。以第k-1阶段至第k阶段的单步状态转移过程为例，根据列车在第k阶段所处节点状态φ(k，i)以及控制级位可求得列车在第k-1阶段所处的实际运行状态（转移过程如图2中蓝色箭头所示），并将所求得状态近似为第k-1阶段处的邻近节点状态[13−14]。

保留φ(k，i)所在运行时间域内每个时间格的最优策略，记录其相关信息（净能耗、运行时间、上一阶段处状态、控制变量等）。当求解到第K阶段处时，在转移至φ(K，0)的所有策略中选取满足|t0+T−t(K，0)|＜ε的最优策略作为输出结果，ε为实际到站时刻与规定到站时刻的最大误差限。更具体地，三维状态空间内的搜索过程如图3所示。

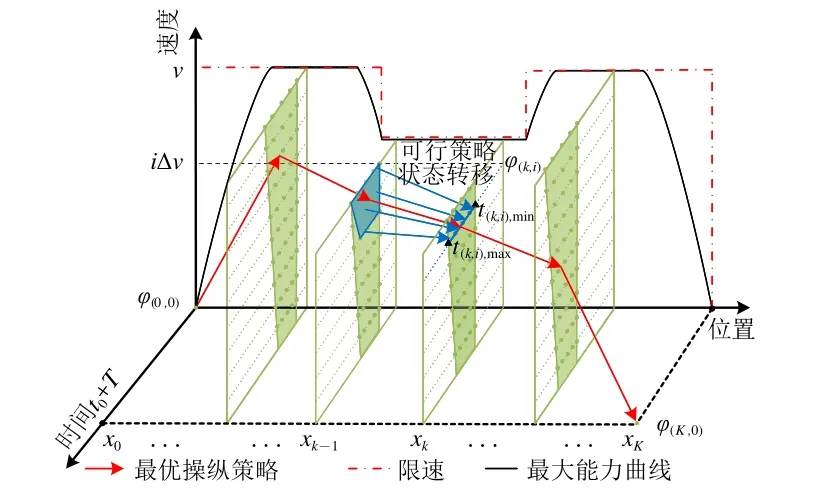
图3 三维状态空间内算法搜索过程

本文动态规划算法根据每个状态所在运行时间域调节Δt，能够有效减小计算量，并得到较为节能以及准点的操纵策略。最后，动态算法程序的步骤总结如下。

步骤1：离散位置−速度状态空间，确定可达搜索区域；离散控制变量u，得到多个控制级位；设置k=1，Et*，net(0，0，1)=0。

步骤2：利用各个控制级位计算第k阶段每个状态处的可达策略集。

步骤3：若k=K，在φ(K，0)处的所有可达策略中选择满足约束|t0+T−t(K，0)|＜ε的最优策略，结束程序；否则，根据式（9）筛选第k阶段每个状态处的可行策略。

步骤4：根据式（10）划分第k阶段每个状态所在运行时间域，并利用式（11）保留每个时间格的最优策略，转至步骤2，进行第k+1阶段的计算。

3 协同操纵全局优化

对运营时间内所有列车的操纵策略进行优化无法保证求解效率，基于分解思想，将全局优化问题进行分解，针对性地优化部分列车在局部时间域的操纵策略。

3.1 运行图时域等效切分

在发车间隔、各区间运行时分和各站停站时间固定的情形下，地铁列车运行图时域等效切分示意图如图4所示。

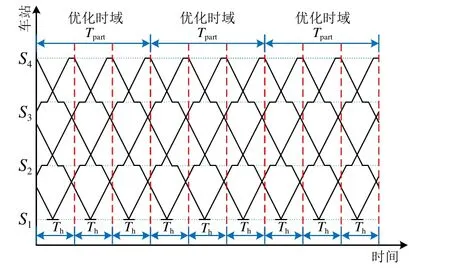
图4 运行图时域等效切分示意图

基于图4所示运行图，各车站具有等时间间隔发车和来车的特点。在此基础上提出1种运行图时域等效切分规则。

每列车的操纵策略相同时，每个时长为Th的时域内列车总运行能耗相等。相同原理，当优化时域时长Tpart为Th整数倍时，即Tpart=aTh（a∈N∗），将运行图全时域以等时间间隔Tpart分割成多个优化时域，并保持不同优化时域对应列车操纵策略一致，则每个优化时域列车总运行能耗是相等的。全时域总运行能耗Eall可近似写为

式中：Epart为单个优化时域总运行能耗，θ为优化时域总数量。

由式（12）可知，当Epart为最小值时，Eall也会是最小值。因此，只需要对单个优化时域内列车操纵策略进行优化，并将操纵策略传递到其他优化时域对应列车，便可完成在全时域内列车操纵策略的优化。

3.2 多列车运行分解

基于前文假设，供电区段功率为供电区段内所有列车运行的总功率[3]。未利用再生能在供电区段上的时间分布可由供电区段功率来获得。依据未利用再生能的时间分布特征，选定各列车运行时应降低运行能耗的区间，从而将全局优化问题进一步分解。为保证再生能的有效利用，各列车所被选定的运行区间应满足的选择条件为：①列车在区间内具有能耗优化空间（即出站牵引时整个供电区段需要从变电站吸收电能）；②列车在区间内运行时供电区段存在未利用再生能；③每个时刻，最多只选择优化1列列车的操纵策略。

最后协同操纵优化方法的流程如下。

步骤1：基于运行图时域等效切分规则，确定优化时域，获取该优化时域供电区段功率数据和时刻表。

步骤2：随时间轴遍历供电区段功率数据，搜索所有存在未利用再生能的时间段（可对到站时刻进行搜寻）；若不存在，结束程序。

步骤3：依据供电区段内未利用再生能所在的时间段，选定各列车运行时应降低运行能耗且处于优化时域内的区间（可对车站发车时刻进行搜寻）；若不存在，结束程序。

步骤4：利用基于多车环境的单车优化方法求解各列车被选定区间的操纵策略；优化完成后，更新供电区段功率数据和各列车操纵策略，并将操纵策略传递到其他优化时域对应列车，转至步骤2。

4 案例分析

4.1 案例基本信息

案例所选取线路为北京亦庄线某供电区段，其内4个车站分别为：荣昌东街（RC）、同济南路（TJN）、经海路（JH）、次渠南（CQN）。具体采用的线路、列车牵引/制动特性以及基本阻力特性相关信息见文献[16]。

列车发车间隔时间为240 s，优化前各列车按牵引能耗最优操纵策略运行。供电区段内各区间运行时分和停站时间如图5所示。图中：D1和D2为列车车次。

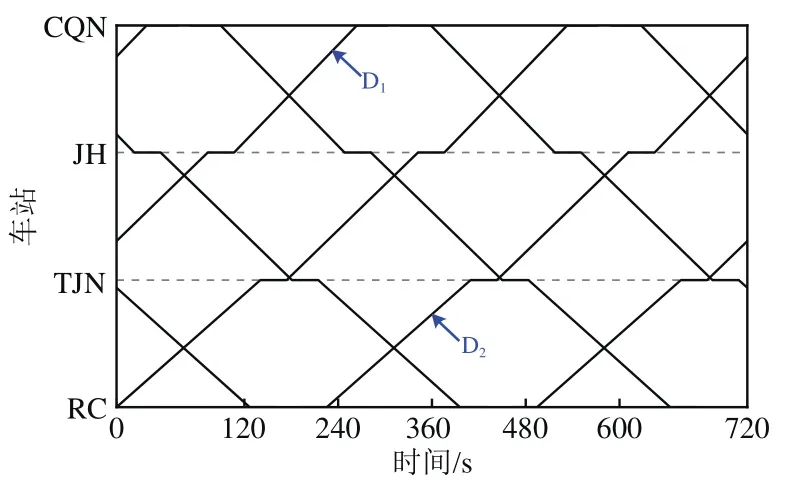
图5 供电区段列车运行图（部分）

4.2 单车操纵优化节能

为了说明本文基于多车环境的单车优化方法的节能性，一方面在供电区段内无再生能可利用的情形下，分别采用本文方法与文献[13]中方法（对照法1）进行节能对比分析；另一方面，在存在再生能可利用的情形下，分别采用本文方法、牵引能耗最优操纵策略（优化前）以及文献[10]中方法（对照法2）进行节能对比分析。

在无再生能可利用时，采用本文方法与对照法1分别求解3个区间列车操纵策略，所得列车运行能耗见表1（由于对照法1未考虑辅助功率，此处列车辅助功率为0 kW）。表中：能耗比为本文方法与对照法1运行能耗的比值；RC-TJN为平缓坡道区间，JH-CQN为长大上坡道区间，CQN-JH为长大下坡道区间。

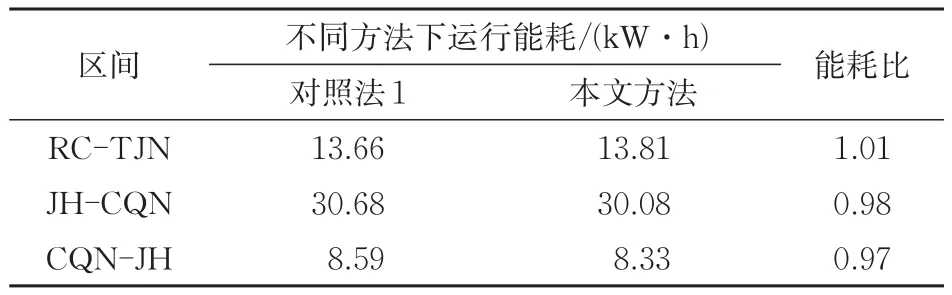
表1 无再生能时运行能耗优化对比

由表1可知：在无再生能利用时，采用本文方法与采用对照法1所得到的运行能耗十分接近。这意味着即便在无再生能的情形下，本文方法同样具有很好的节能效果

在存在再生能可利用时，为评估本文方法的节能效果，依据区间坡道的不同，选取2个典型的实例进行优化分析。实例1为D1列车在区间JHCQN运行，辅助能耗为11.67 kW·h；实例2为D2列车在区间RC-TJN运行，辅助能耗为13.67 kW·h。2个实例分别采取本文方法和对照法2进行优化，并与优化前进行比较，不同操纵策略下列车运行能耗见表2。

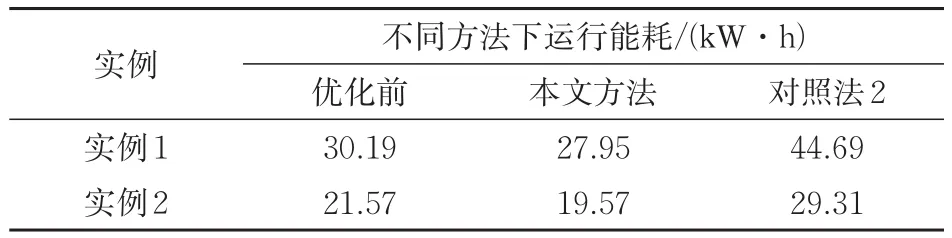
表2 有再生能时运行能耗对比

由表2可知：采用本文方法时，实例1与实例2列车运行能耗相较于优化前分别下降7.42%与9.27%；而由于供电区段内列车可利用再生功率较小，对照法2对比优化前出现了运行能耗增加的情况。

为了进一步说明，本文方法与对照法2优化上的同异，不同操纵策略下，实例1列车的运行过程如图6所示。

图6 不同操纵策略下实例1列车运行过程

从图6可以看出：对照法2是通过预先设定列车运行策略，增加列车之间牵引-制动重叠时间来达到节能目的，但为了克服陡坡的附加阻力以及满足准点运行的约束，对照法2过于延长了列车的最大牵引工况时间，从而使得运行能耗比优化前有所提升；本文方法在综合考虑实际线路条件和可吸收再生能时间分布的基础上，确定列车运行过程中所应施加的最优控制级位，使得列车不仅能够以合理的运行工况经过坡道，同时也能极大程度利用可吸收再生能，因此能有效降低运行能耗。此外，从图6（a）可以进一步看出，和优化前的运行曲线相比，为了兼顾列车准点运行和再生能的吸收，本文方法和对照法2都会导致列车出站牵引时的末速度更低，而停车制动时的初速度更高。

从上述分析中可以得出：基于多车环境的单车优化方法能够根据列车运行时的实际线路条件和可吸收再生能的时间分布得到较为节能的操纵策略。

为了探究列车利用再生能时的节能控制方式，以实例2为例，对平缓坡道区间列车操纵策略的优化进行分析。实例2中，列车在采用本文方法操纵策略和优化前操纵策略后的运行过程如图7所示。

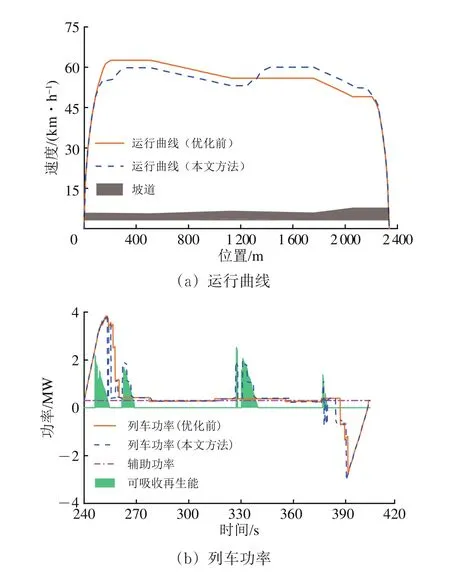
图7 不同操纵策略下实例2列车运行过程

从图7可以看出：与仅采用最大牵引工况利用再生能的研究[7，10]相区别，采用本文方法操纵策略后，在再生能存在的时段，列车功率与可吸收再生功率十分接近；而在无再生能的时段，列车操纵策略则与优化前基本一致。这表明：在列车利用再生能时，根据实际可吸收再生功率来决定对列车所需要施加的牵引力是1种较为节能的操纵方式，能够避免因列车功率与实际可吸收再生功率偏差较大而造成的不必要能量损耗。

4.3 全局优化节能

采用协同操纵优化方法对供电区段内上下行所有列车进行协同优化。方法中优化时域为图5中列车运行的时间范围（Tpart=720 s）。方法共迭代优化了3次，优化前后优化时域能耗对比见表3。

表3 优化前后能耗对比 kW·h

由表3可知：优化后，总再生能耗提升约10.98%；为了克服列车在运行过程中增加的运行阻力能耗，总牵引能耗相对于优化前提升1.80%；综合总再生能耗和总牵引能耗提升的影响，最后列车总运行能耗节约4.01%。

优化前后供电区段功率对比如图8所示。图中：供电区段功率正值为未利用再生功率，负值则为从变电站吸收电能。

图8 优化前后供电区段功率对比

由图5和图8可以看出：在0～650 s内，通过优化列车操纵策略，供电区段内的再生能基本被吸收殆尽；而在其他时间段，由于不存在优化操纵的列车，因而供电区段的功率没有发生变化。这说明协同操纵方法能够有效地减少供电区段未利用再生能，但受限于分解优化会导致问题难以找到最优解的局限性，无法保证再生能全部得到利用。

为了更直观地展示经协同操纵优化方法优化后列车之间的协同效果，200～600 s供电区段内所有列车的运行曲线如图9所示（优化过程中只有上行列车操纵策略被选定优化）。

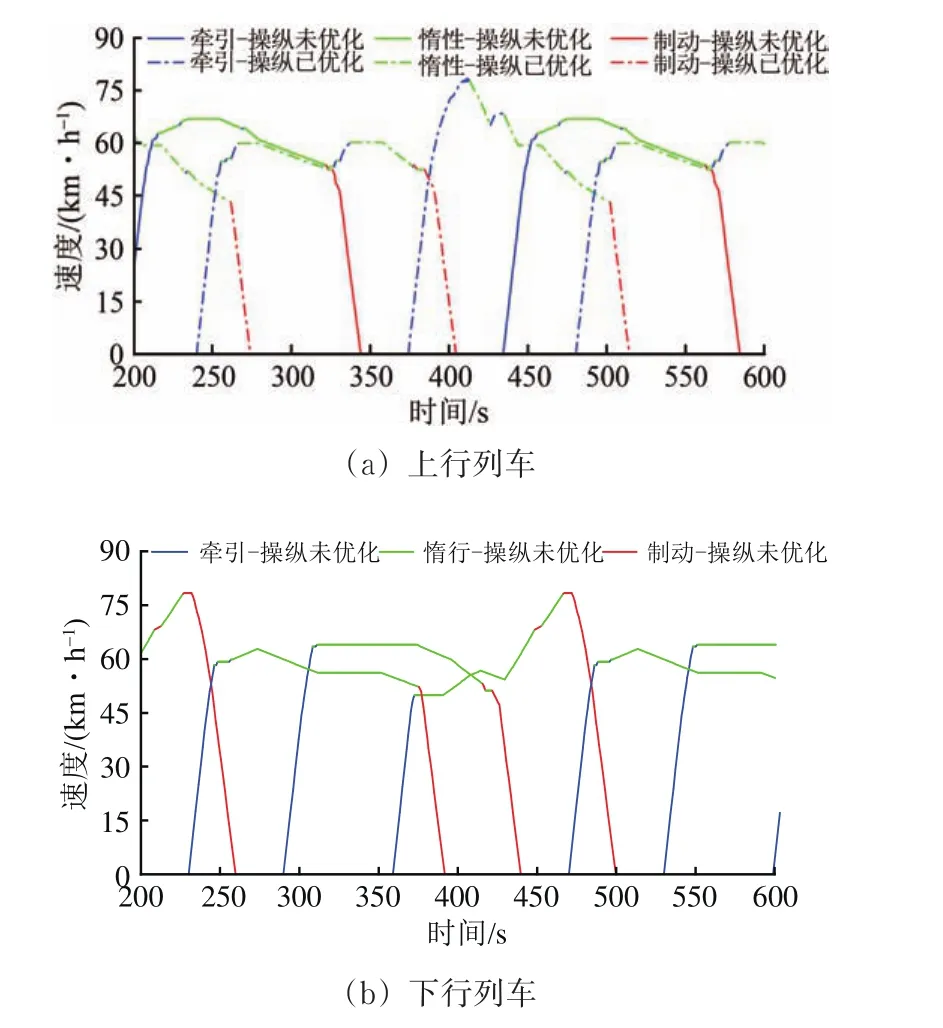
图9 列车协同运行曲线

从图9可以看出：为实现列车间的协同操纵，各列车在其他列车制动的时间段进行了合理的牵引过程，以利用再生能；而在没有列车制动的时间范围，除了出站牵引阶段和停车制动阶段，列车基本保持惰行工况，以降低牵引能耗。因此，协同操纵优化方法能够在不调整时刻表前提下实现列车之间较优的协同节能效果。

5 结 语

考虑多车环境下单车运行节能优化，以外部功率表征其他列车的影响，构建外部功率确定下的节能操纵优化模型，并设计1种在非均匀离散三维空间内寻优的动态规划算法精确求解，从而实现单车操纵优化。案例分析表明：基于多车环境的单车优化方法能够根据列车运行时的线路条件和可吸收再生能的时间分布得到较为节能的操纵策略，有效降低列车运行能耗；在列车利用再生能时，依据可吸收再生功率的实际大小来决定对列车施加的牵引力是1种较为节能的操纵方式。

基于分解思想，提出1种运行图时域等效切分规则，缩小了协同操纵优化的时间范围，并进一步结合供电区段内未利用再生能的时间分布特征，选定各列车应降低运行能耗的运行区间，将协同操纵全局优化问题分解为了一系列多车环境下单车区间操纵优化的子问题。协同操纵优化方法通过迭代地分解全局优化问题，并对子问题进行求解，实现列车间的协同操纵。案例分析表明：在不调整时刻表的前提下，与优化前总牵引能耗最小运行方式相比，采用本文协同操纵优化方法，能够实现列车之间较优的协同节能效果，有效地提升总再生能耗，并降低4.01%的总运行能耗。

由于文中对直流牵引供电系统的模型进行了简化，这可能会影响计算结果，下一步将考虑采用实际的供电系统模型对多列车操纵策略进行协同优化。