基于功率曲线时域特征和变分模态分解的S700K转辙机运行状态诊断算法

魏文军，李 政，武晓春

（1.兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070；2.兰州交通大学 光电技术与智能控制教育部重点实验室，甘肃 兰州 730070）

S700K转辙机作为实现线路转换的关键设备，广泛应用于高速铁路中的提速道岔，其若发生故障，将会严重影响高速列车行车安全[1]。道岔动作过程由室内控制电路和室外动作设备共同作用完成，为保障道岔正常动作，铁路部门主要采用故障维修和计划检修2种策略，但这2种策略也存在着检修过剩、维修经验不足和安全风险大等问题[2]。如果能对S700K转辙机在整个运行周期内的运行状态进行实时监控与诊断，在故障发生前及时检修，在故障发生后及时定位并维护，则可大大提高道岔检修和维护的效率，降低因转辙机故障而导致列车事故的概率。近年来，已有大量关于S700K转辙机智能故障诊断的研究[3−6]，但主要集中在故障发生后的问题分析定位等方面，关于转辙机整个运行周期内的状态诊断研究则相对匮乏。

为实现S700K转辙机在整个运行周期内的状态诊断，首先需要提取反映其状态的信号特征，然后基于特征信息进行运行状态诊断分析。在特征提取方面，杨菊花等[7]对S700K转辙机电流和功率曲线进行哈尔小波变换，然后与原始数据组成原始特征矩阵，再经BP神经网络训练实现特征矩阵的降维，但训练参数选择困难，同时输入曲线受迭代次数的影响，运算速度较慢。黄世泽等[8]选用几种典型曲线，利用弗雷歇距离定义相似度函数，将样本曲线之间的相似度作为特征信息，但对典型曲线的要求较高，信号特征单一。申中杰等[9]提出利用不受个体差异影响的时域特征相对均方根值作为特征指标，但存在信号提取不充分，不能体现信号之间细小特征的问题。

在运行状态诊断方面，陆桥等[10]提出基于灰色关联分析的转辙机故障诊断方法，受转辙机个体差异和外部环境的影响，存在门限值选择困难、实用性差等问题。许庆阳等[11]根据转辙机连续运行功率数据特点，提出利用隐马尔科夫模型建立转辙机故障类型映射数据集，但需要大量关于转辙机正常和故障的监测数据，而现场中转辙机故障的实际监测数据很少。

利用变分模态分解 （Variational Mode Decom⁃position，VMD）可提取得到滚动轴承振动信号故障信息[12]。与哈尔小波变换、弗雷歇距离定义相比，该方法在状态特征提取中具有自适应强、运算速度快，特征提取充分等优势。排列熵（Permuta⁃tion Entropy，PE）是衡量信号复杂度的方法，对信号突变敏感，已成功应用于航空发动机、变压器等设备的振动信号特征提取[13−14]。将VMD和PE相结合，能够有效提取设备的S700K转辙机功率曲线的细小状态特征。建立在统计学理论基础的模糊聚类分析，能够利用所提取样本特征间的相似度实现小样本数据分类，现已成功应用在电力等行业的设备状态诊断中[15−16]，在转辙机运行状态诊断时可借鉴采用该方法。

本文提出关于S700K转辙机运行状态诊断算法：首先，从信号集中监测设备中获取S700K转辙机功率曲线，计算信号序列的有效值、峰值因子和峭度因子，并将其作为时域特征值；然后，利用VMD算法进行原始信号频域分解，并结合排列熵算法计算不同模态分量函数，得到4个频域特征值；最后，将S700K转辙机在不同运行状态下的时、频域7个特征值组成特征数据集，并作为输入矩阵进行模糊聚类分析，实现S700K转辙机全周期运行状态（正常、亚健康、故障和严重故障）诊断。以现场实例进行验证分析，该算法能够有效诊断S700K转辙机的运行状态。

1 状态诊断算法

1.1 VMD算法

VMD算法是最早由Dragomiretskiy等人提出的自适应信号处理方法[17]，在一定约束条件下，通过不断迭代更新模态函数的中心频率和有限带宽，实现原始信号频率的有效分解。与经验模态分解（EMD）相比，VMD解决了模态混叠的问题，具有较强的鲁棒性。VMD的分解过程可分为变分约束问题构造和求解2大步骤，具体如下。

（1）变分约束问题构造。假设k为分解后模态函数的个数；t为原始信号的时间变量；u（kt）为模态函数，每个模态函数的中心频率为wk，有限带宽为D。变分约束问题可描述为模态函数分量的有限带宽之和最小，并且各模态函数分量相加等于原始信号（ft）。

VMD算法的求解流程如图1所示。图中：b为迭代次数。求解时，通过式（4）和式（5）的“鞍点”更新模态分量uk（t）和中心频率wk，中间变量拉格朗日算子λ（t）也随之不断更新。最终，在噪声容忍度为σ、收敛精度为ε下，获取k个带宽之和最小的模态函数分量。

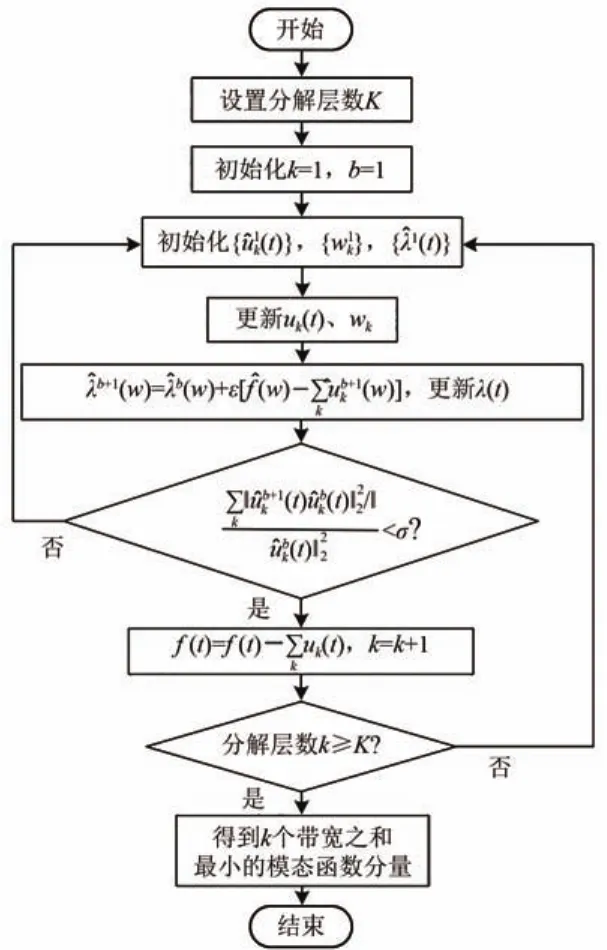
图1 VMD算法流程图

1.2 排列熵(PE)

从熵值的定义可知：熵值越大，表示信号序列越复杂；熵值越小，表示信号序列越不规则。

在实际应用中，时延参数τ、嵌入维度m的选择对计算量和计算精度有影响，为提供信号序列有效特征信息。根据文献[20]取采样序列s≥5m！。监测中心对S700K转辙机的采样周期为40 ms，采样序列s等于采样时间除以采样周期，以S700K转辙机正常运行为例，采样时间为7 s，则采样序列s为175，m取值为4，τ一般小于2。

1.3 模糊聚类分析

采用传递包算法建立S700K转辙机运行状态诊断模型。首先利用研究对象的特征指标构建初始模糊特征矩阵；然后为消除不同量纲之间的影响，对其进行标准化处理；之后引用指数相似系数法构建模糊相似矩阵；最后当模糊等价矩阵中置信因子ϖ从大到小变化时形成动态聚类图。具体算法步骤如下。

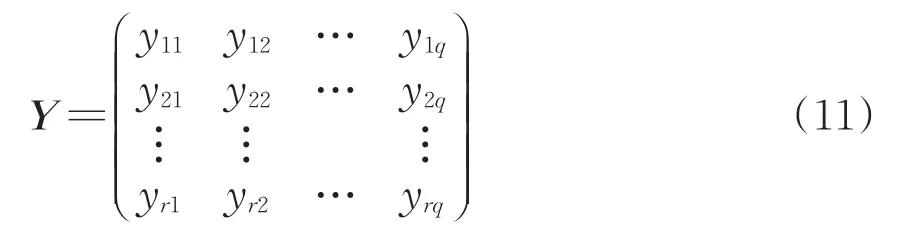
1）步骤1：建立初始模糊特征矩阵Y

设论域U={y1，y2，…，yr}为S700K转辙机r个不同运行状态，每个运行状态下有q个指标表征其特征，即

由此，可将初始模糊特征矩阵表示为

2）步骤2：模糊特征矩阵标准化处理Y″

在实际应用中，为实现不同量纲指标之间的数据比较，需要对初始模糊特征矩阵进行标准化处理，使得矩阵数据落到区间[0，1]上。变换方式由以下2步完成。

（1）标准化，计算式为

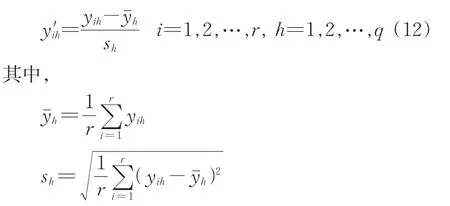
（2）极差化，计算式为

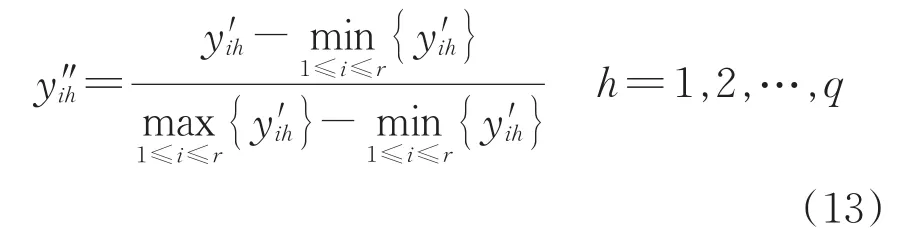
3）步骤3：构建模糊相似矩阵R

为定量描述样本之间的相似程度，引用聚类统计量来计算数量指标，通常用于聚类统计量的计算方式有：夹角余弦法、海明距离法、切比雪夫法以及指数相似系数法等方法。本文选用对细小特征敏感的指数相似系数法建立模糊相似矩阵，即

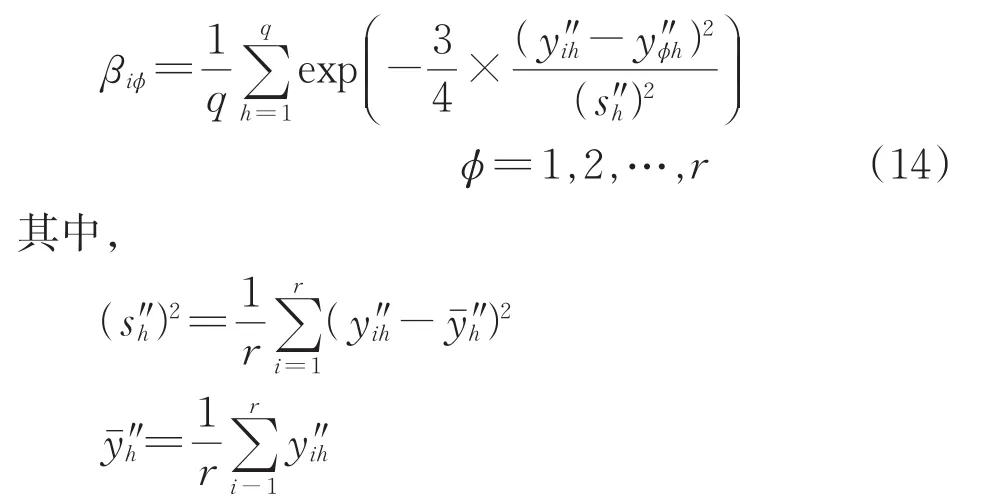
对模糊标准矩阵Y″中计算不同行之间的聚类统计βiφ，其中i和φ为模糊标准矩阵所在行数，并以聚类统计βiφ建立模糊相似矩阵R。

4）步骤4：形成动态聚类图

上述建立的模糊相似矩阵不一定具有传递性，为实现聚类分析，采用传递包算法建立模糊等价矩阵R*。在模糊相似矩阵R中，当经过次传递包计算后，使得。其中利用平方法计算传递包，即

模糊等价矩阵R*具有传递性，当其中的聚类统计量βiφ随置信因子ϖ∈[0，1]从大到小变化时，由式（16）形成动态聚类图。

当置信因子由1到0变化时（计算机自动按0.001的步长减小），针对动态聚类图中故障库（已知状态类型）和测试库的聚类情况，通过自动匹配分类样本集和测试集中的曲线类型，进而实现S700K转辙机运行状态诊断的目的。

2 转辙机运行状态诊断方法

S700K型转辙机在转换过程中，输出功率P与转辙机推力F之间的关系为

式中：Re为等效力臂，N·m−1；n为转速，r·s−1；η为转换效率，%。

根据S700K转辙机型号可知其电机的等效力臂，转速和转换效率为定值，由式（17）得到其输出功率和推力间呈正比关系。由此判定：S700K转辙机动作功率曲线特征与转换过程的运行状态具有一致性，体现着其机械性能，是状态诊断的重要指标；同时S700K转辙机功率曲线具有非线性、非平稳的特点；每1种运行状态下的动作功率曲线特性也不相同。因此可将其功率曲线用于状态诊断。

功率曲线的有效值体现了其能量特征，曲线波动越大，对应的值越大；峰值因子用于衡量曲线冲击特性，检测曲线峰值；峭度因子描述了信号序列的概率密度，用于对比曲线异常持续时间。因此选取S700K转辙机在不同运行状态下的典型功率曲线，计算其有效值、峰值因子和峭度值3个因子作为时域特征值。对于时域特征不明显的曲线，利用变分模态分解算法进行频域分析，并将4个不同模态函数的排列熵作为频域特征值。以时、频域共计7个特征值进行模糊聚类分析，能够实现S700K转辙机的运行状态诊断。诊断过程如图2所示。

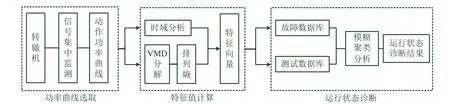
图2 S700K转辙机运行状态诊断示意图

由图2可知，S700K转辙机状态诊断流程主要由功率曲线选取、特征值计算和运行状态诊断3步组成。具体如下。

1）功率曲线选取

通过监测流过启动继电器（1QDJ）的电压和电流实现对S700K转辙机功率曲线的采集，将S700K转辙机运行状态分为正常、亚健康、故障和严重故障4种；在每种运行状态下，按照转辙机的故障程度和动作异常阶段选取典型样本功率曲线；经整理每种运行状态下有多个典型样本功率曲线，由此来建立故障数据库。

2）特征值计算

以信号序列X={x(ζ)|ζ=1，2，…，s}表示1条针对S700K转辙机的功率曲线，其有效值μ1、峰值因子μ2和峭度因子μ3计算式分别为

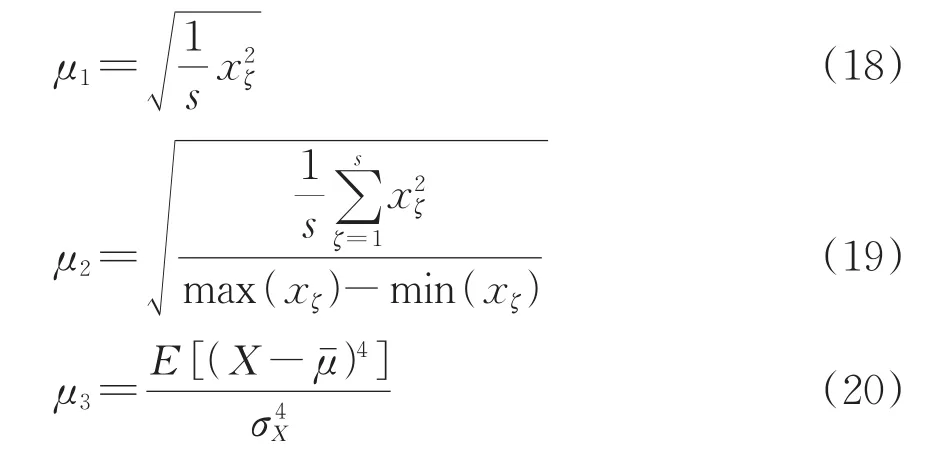
对功率曲线进行频域分析时，利用VMD算法将功率曲线分解为4个具有不同频率特征分解分量，并计算每1模态函数分量的排列熵，用于描述每1层分解分量的信号复杂度。

3）运行状态诊断

经时域、频域分析将其7个特征值作为对应功率曲线下的特征向量，将测试曲线和故障数据库中典型样本功率曲线进行模糊聚类分析，实现S700K转辙机运行状态诊断。

3 实例计算与分析

3.1 S700K转辙机功率曲线

以兰州铁路局集团有限公司信号集中监测中心关于S700K转辙机功率曲线的历史样本数据为例，在正常运行状态下，动作功率曲线分为解锁、转换和锁闭3个阶段；亚健康运行状态下，动作功率曲线开始出现振动和不平稳现象，但能够完成转换；故障状态下，转辙机完成转换后，无法正常表示功率曲线；在严重故障状态下，转辙机无法完成正常转换。

以不同运行状态下的典型样本功率曲线建立故障曲线库，如果测试曲线在故障曲线库中没有记录，则将其作为样本曲线加入库中，比如，1条新的测试曲线对应的状态是1种亚健康，则将其命名为“亚健康3”加入库中。S700K转辙机全周期运行下的典型样本功率曲线如图3所示，对应分析见表1。

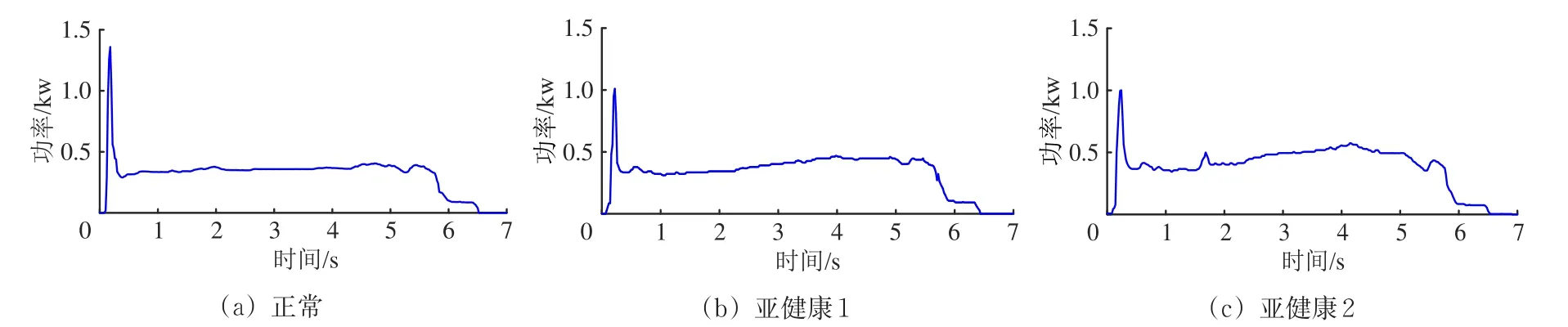
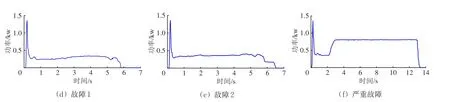
图3 S700K转辙机典型样本功率曲线

表1 S700K转辙机典型样本功率曲线分类及其特征

3.2 功率曲线的时域特征值计算

对图3所示的6种典型样本功率曲线进行时域分析，即采用式（18）—式（20）分别计算其3个时域特征值，结果见表2。定义指标数值之间的相差阈值超过±1时，认为曲线之间有显著差异；每种功率曲线至少要有1种特征值之间的相差阈值超过±1，后续的状态诊断算法才能有效进行。从表2可知：部分运行状态间的特征值相差阈值超过±1，时域特征差异较为明显；部分运行状态间的时域特征差异不明显，如表中的“正常”状态和“故障2”状态。对于时域特征值差异不明显的功率曲线，仅采用时域特征值对转辙机状态进行模糊聚类诊断，则可能造成诊断错误，因此还需要引入频域指标。

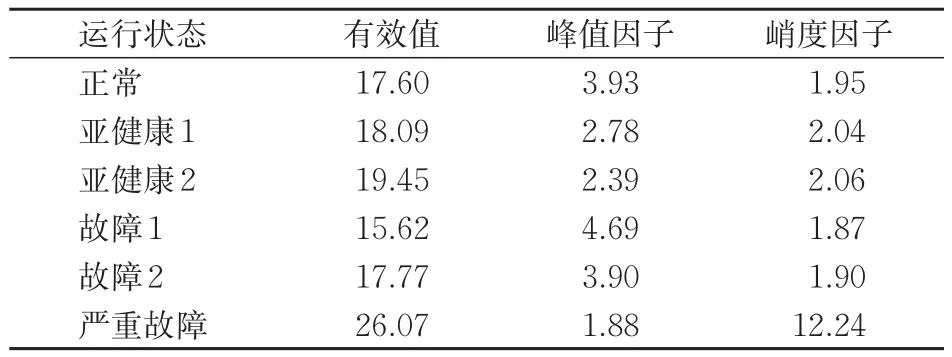
表2 典型样本功率曲线时域特征值

3.3 功率曲线的频域特征值计算

采用VMD算法进行频域分析，并结合排列熵算法表征其特征值。在进行VMD分解之前，需要先确定分解层数K和惩罚因子α。参考文献[21]选取分解层数方法，对“亚健康1”状态下的功率曲线进行局部均值分解（LMD）后，分解后得到5个乘积函数分量（Product Function，PF），以具有明显波动信息的分解分量作为分解层数，分解结果如图4所示。

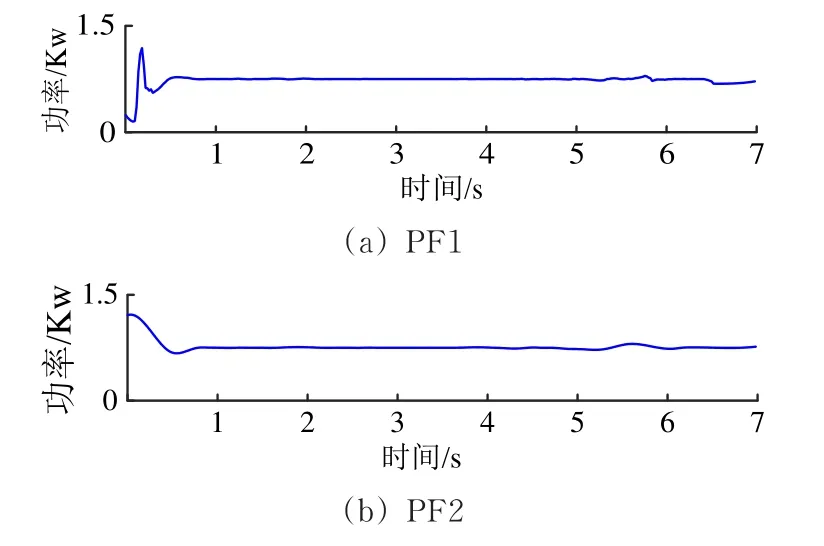
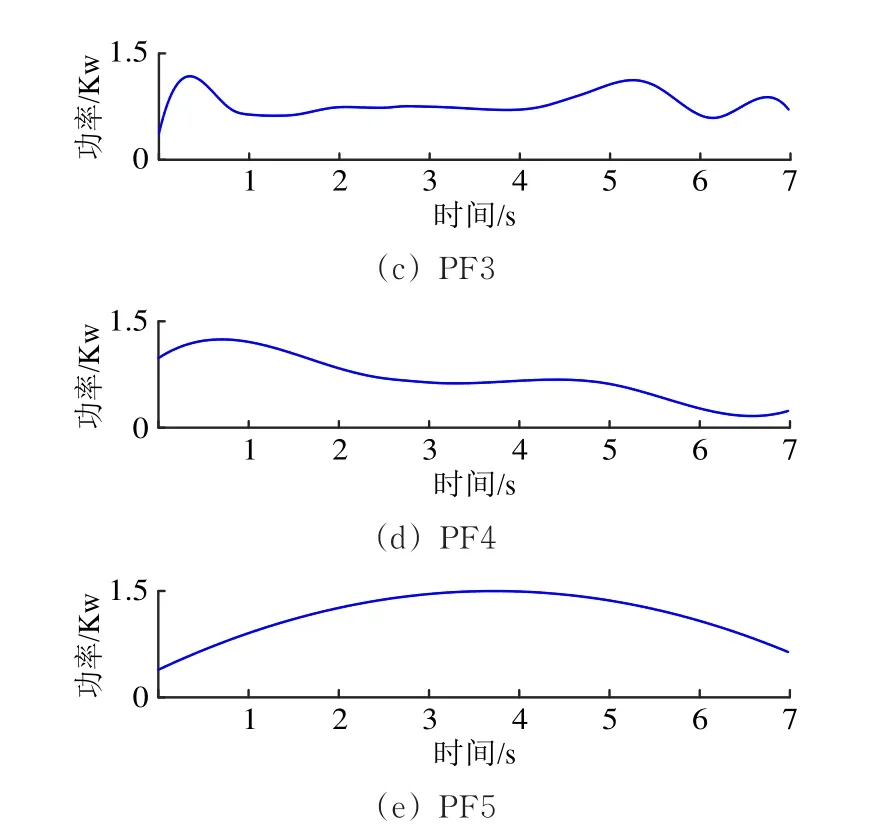
图4 S700K转辙机“亚健康1”运行状态下功率曲线的LMD分解

由图4可知：当分解到PF5分解时，信号序列中没有足够的极值点，可以判定前4层为主要有效信息。以中心频率法实验不同惩罚因子α的取值，当选择α=1 000时，此时中心频率的差异大，信号识别度高。因此取K=4，α=1 000对不同运行状态下S700K转辙机功率曲线进行VMD分解。

对图3所示的6条功率曲线，按照图1中流程图进行VMD处理，分解后得到4个有限带宽的固有模态函数（BIMF）。不同运行状态的同一BIMF频率分布中心相似，且频谱幅值的差异性较小，这里仅给出“亚健康1”和“亚健康2”运行状态下动作功率曲线的模态函数分量BIMF1—BIMF4，如图5和图6所示，对应频率分布如图7和图8所示。

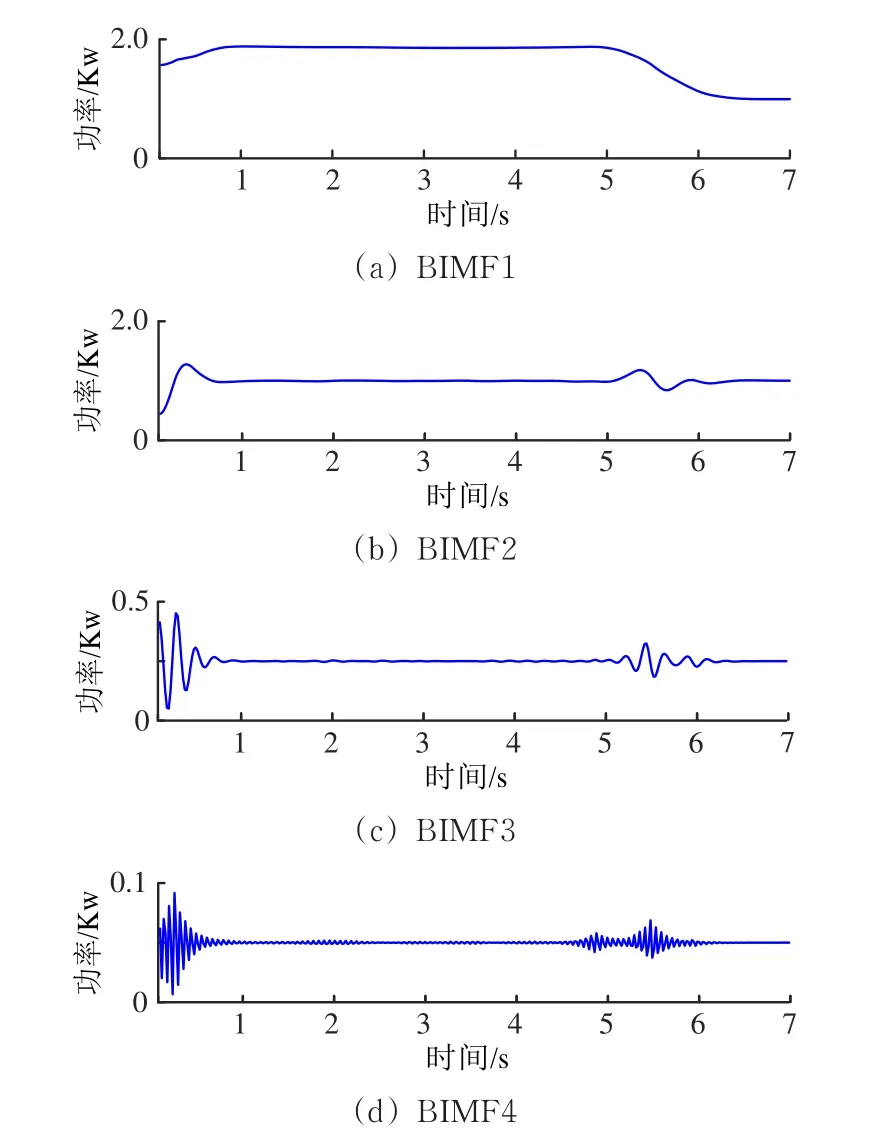
图5 “亚健康1”状态下动作功率曲线的模态函数分量

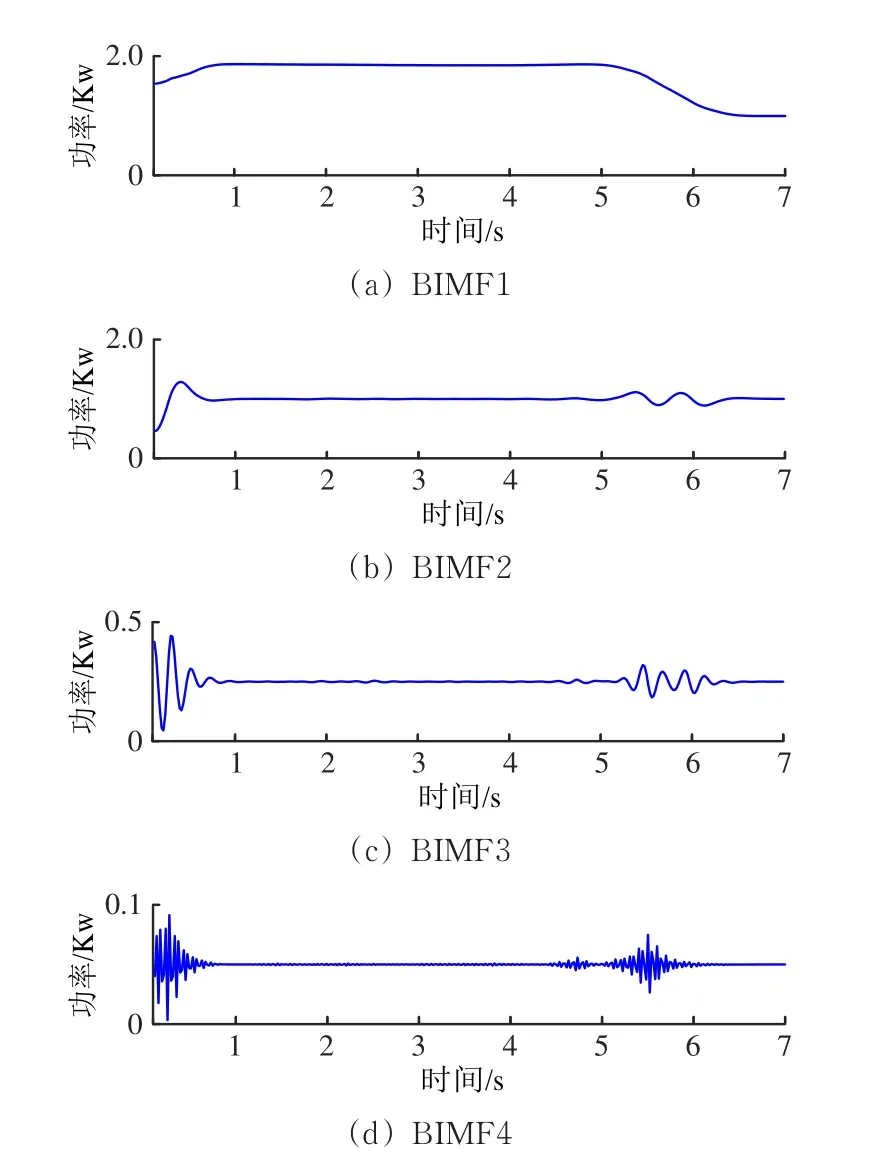
图6 “亚健康2”状态下动作功率曲线的模态函数分量

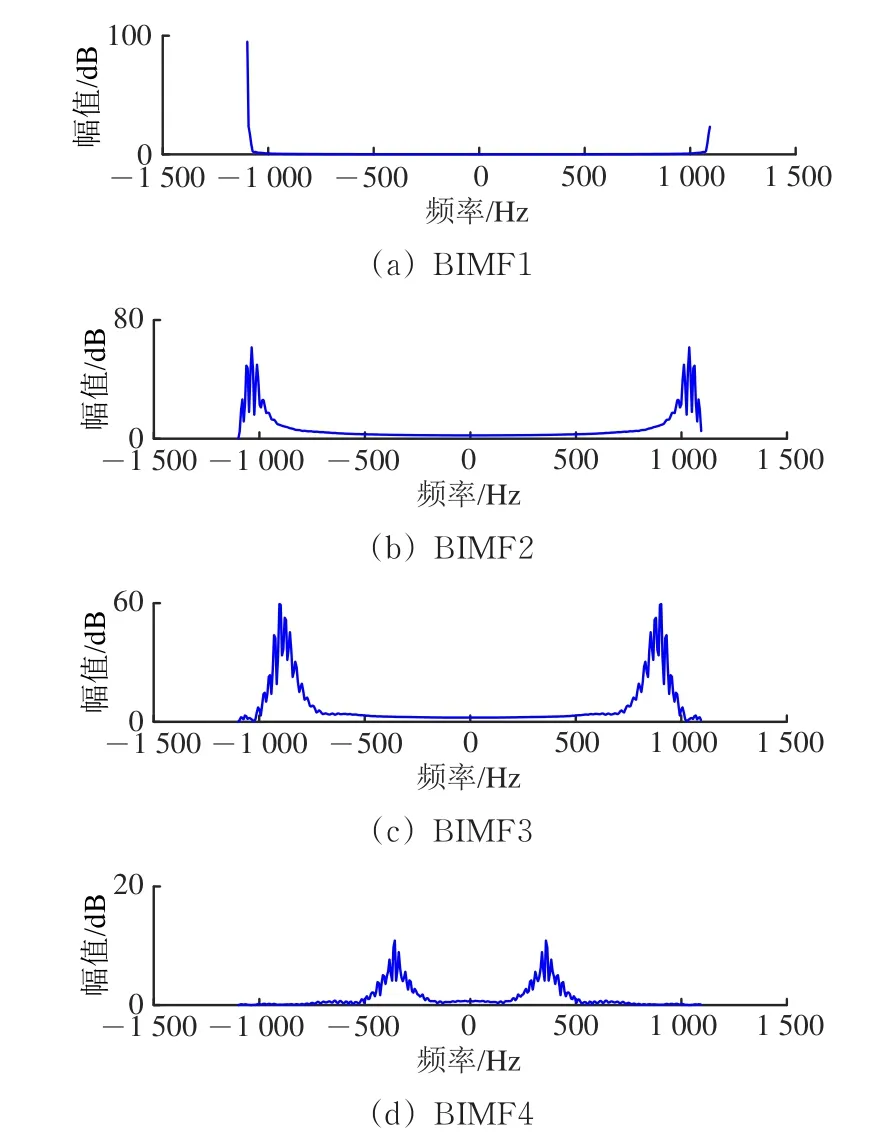
图7 “亚健康1”状态下模态函数分量的频率分布

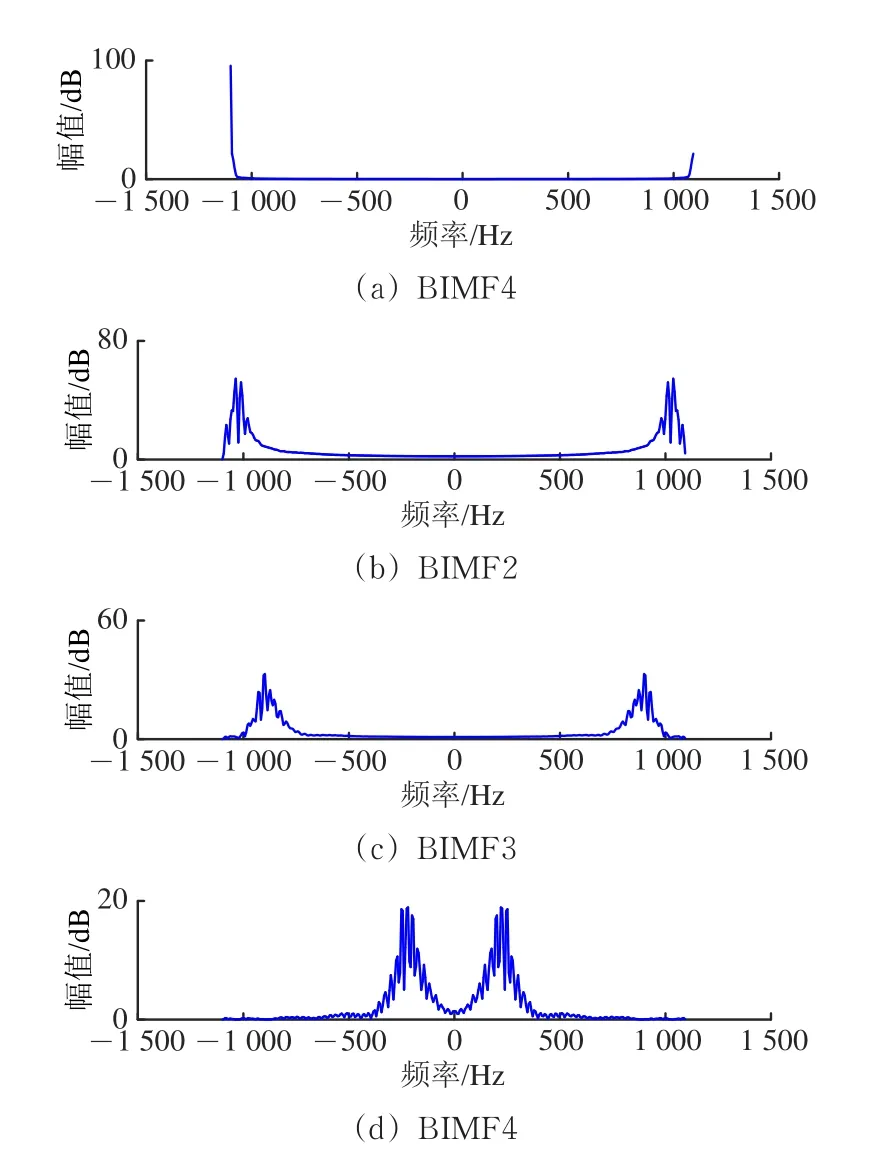
图8 “亚健康2”状态下模态函数分量的频率分布

由图7和图8可知：同一运行状态的不同BIMF函数频谱分布中心不同，如图7中BIMF1包络谱的中心频率高于1 000，BIMF2—BIMF4的中心频率依次降低。为充分表征不同运行状态下VMD分量的有效特征，引用排列熵（PE）计算模态分量，用于描述各分量的信号复杂度。图3所示的6条样本功率曲线的排列熵见表3。

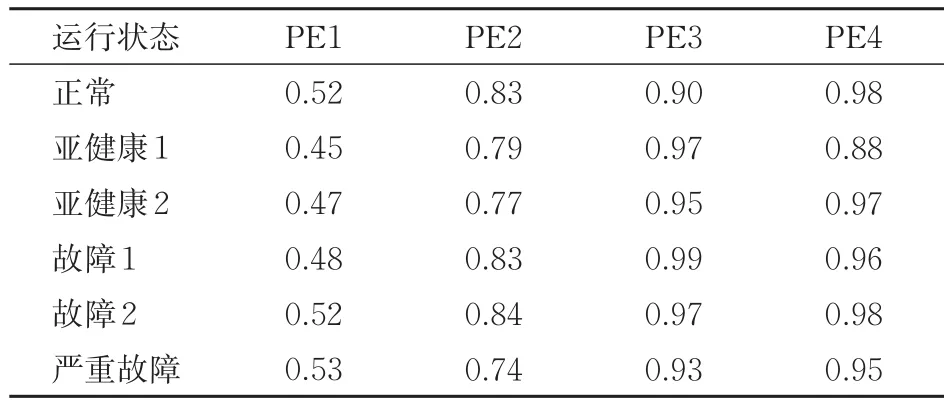
表3 典型运行状态下功率曲线频域特征值

将同一固态模态函数分量下的不同状态类型的熵值作为参数，形成柱状图如图9所示。由图9可以看出：亚健康状态中回路电流过大和转换阶段振动的BIMF4分量排列熵值存在一定差异，故障状态中二极管短路和整流堆开路的BIMF1分量排列熵值存在一定差异。由此可知，根据不同运行状态下功率曲线时、频域特征值的差异性，利用时域特征结合VMD排列熵的频域特征作为状态特征时，能够有效提取S700K转辙机的运行状态特征参数。

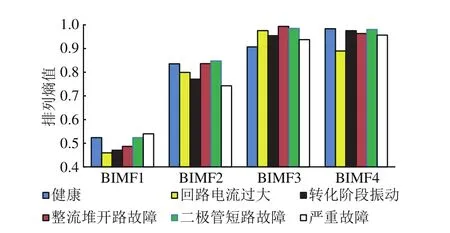
图9 S700K转辙机运行状态VMD分量排列熵柱状图

3.4 S700K转辙机模糊聚类分析

对于图3所示的6条功率曲线，分别以f1—f6表示由其7个特征值构成的特征向量，并进行模糊聚类分析，具体步骤如下。

步骤1：建立初始模糊特征矩阵Y

步骤2：采用式（12）和式（13）对式（21）进行标准化处理，得到的模糊标准矩阵Y″为

步骤3：采用式（14）对模糊标准矩阵Y″进行相似度计算，建立模糊相似矩阵R为

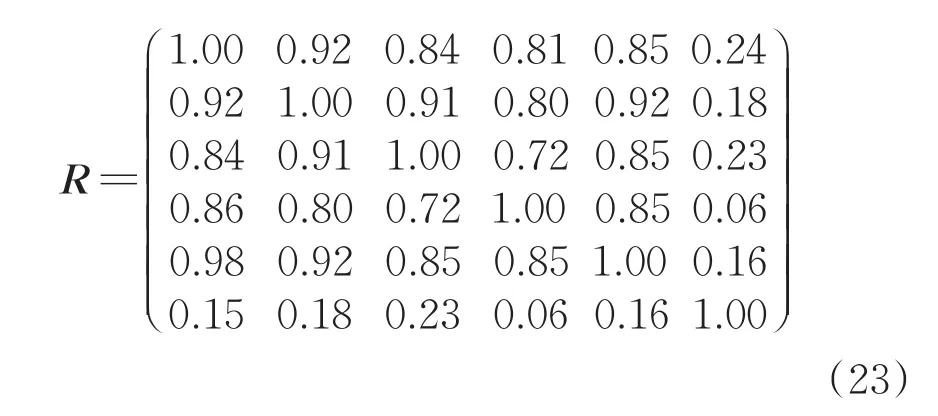
步骤4：形成动态聚类图，用传递包法建立模糊等价矩阵R*，即t（R）=R*；利用式（16）建立相应等价布尔矩阵Rϖ，当置信因子ϖ从大到小变化时进行聚类，并形成动态聚类图，完成S700K转辙机运行状态诊断。

3.5 实例应用

为验证S700K转辙机运行状态诊断方法的有效性，随机选取兰州铁路局集团有限公司信号集中监测中心关于S700K转辙机在“亚健康2”状态和“严重故障”状态下共2条动作功率曲线作为待检曲线，命名为待检曲线1和待检曲线2，其动作功率曲线如图10所示，经时、频域分析后的特征值见表4。

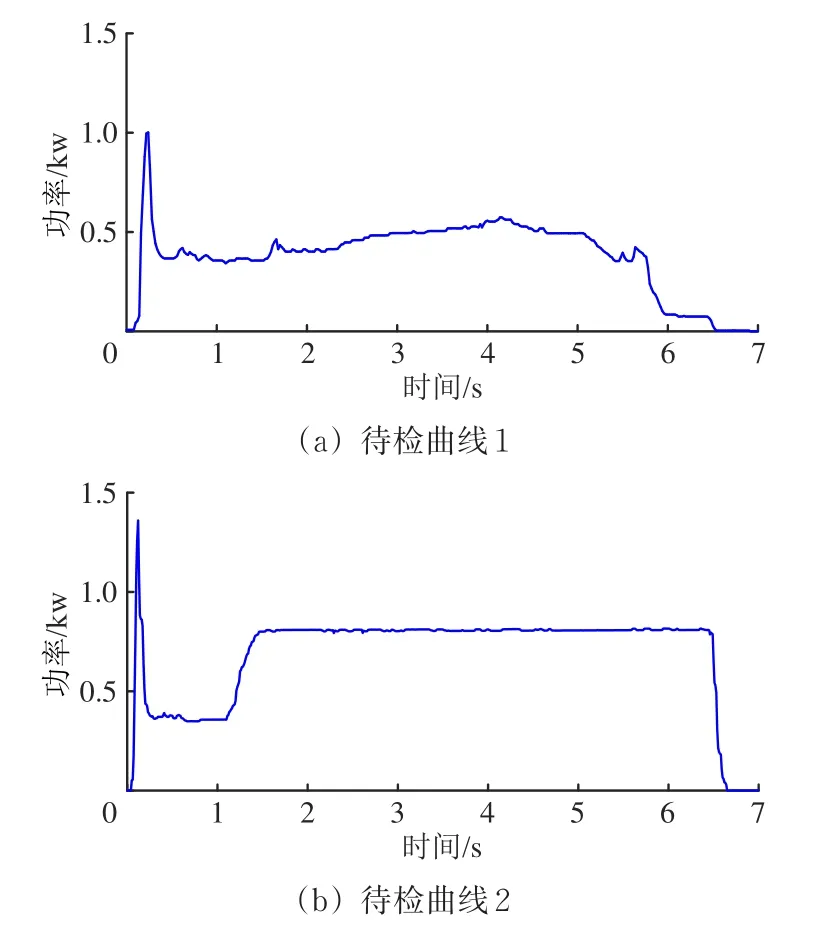
图10 待检动作功率曲线

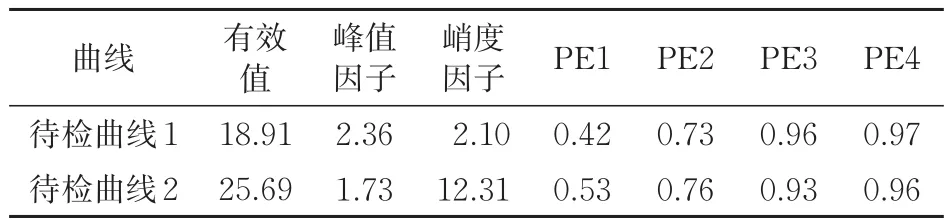
表4 待检动作功率曲线时频域特征值

以fd1和fd2分别表征由表4中S700K转辙机待检功率曲线的时、频域特征值构成的特征向量，并且输入S700K转辙机运行状态诊断模型进行模糊聚类分析，形成动态聚类图如图11所示。

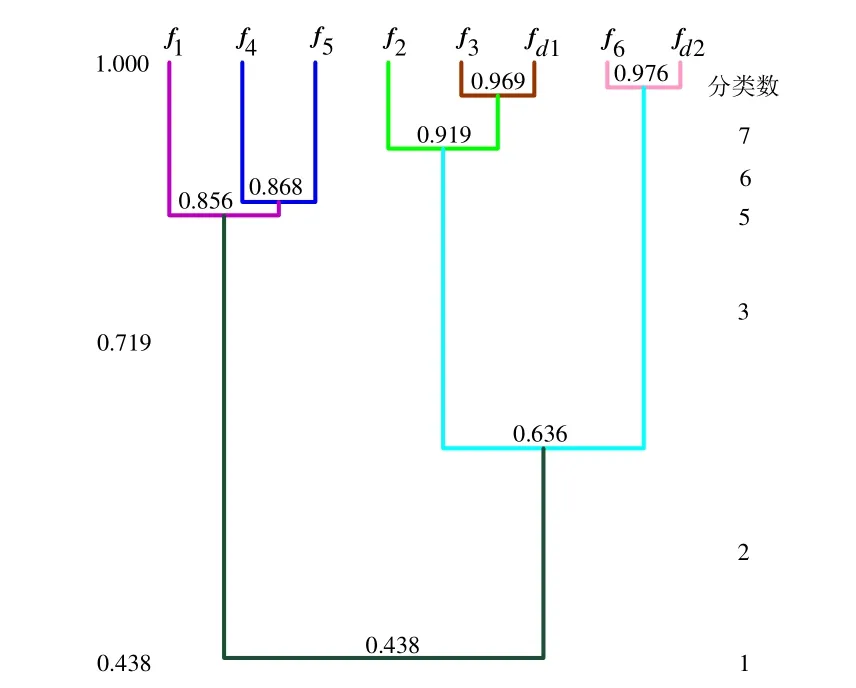
图11 测试集运行状态诊断动态聚类图

由图11可知：左侧为置信因子ϖ的取值，当ϖ从1变化到0时，等价布尔矩阵Rϖ相同的列被归为一类，最终右侧分类数归为一类；当置信因子ϖ变化到0.969时，f2和d0分为一类，则测试样本d0和故障库中典型样本功率曲线f2属于同一运动状态，因此d0被诊断为“亚健康2”运动状态；同理，当置信因子变化到0.976时，测试样本d1和故障库中典型样本功率曲线f5属于同一运动状态，因此d1被诊断为严重故障运动状态，符合现场检测结果。

选取60组曲线，采用本文方法，以MATLAB软件对功率曲线进行诊断，并将诊断结果与现场工作日志进行对比，本文算法诊断率为98.33%，说明提出的方法具有一定的实用意义。由于程序运行时间和故障库的大小有关，经测试故障库为30条曲线时，运行时间不超过1.5 s，从而证明了该算法的时效性。

4 结 论

（1）针对S700K转辙机运行状态与其动作功率曲线之间的关系，提出时域特征结合VMD排列熵频域特征的S700K转辙机运行状态模糊聚类分析算法。

（2）为提取功率曲线细节分量，利用有效值、峰值因子和峭度因子指标来计算曲线时域特征，并结合VMD分解后的排列熵作为其特征，实现了功率曲线微小特征信息的表征。

（3）S700K转辙机全周期运行状态诊断中，模糊聚类分析算法不需要训练，即可实现对状态类型的诊断识别，适合S700K转辙机样本少的特点。

（4）实例结果表明该算法的诊断率为98.33%，实现了S700K转辙机全周期运行状态（正常、亚健康、故障和严重故障）诊断，为其维修、维护提供了理论支持。