基于动车组车载变压器频率响应优化模型的故障定位

吴振宇，周利军，王东阳，张桂南，于兴宇，江飞明，周 猛

（1.西南交通大学 电气工程学院，四川 成都 611756；2.中国铁道科学研究院集团有限公司 机车车辆研究所，北京 100081）

车载变压器作为动车组核心的电气设备之一，担负着电能供应和电压等级转换的任务[1]。相比于陆地变压器，车载变压器的运营环境更加恶劣（受限于动车组有限的空间，车载变压器的铁芯与绕组采用卧式结构装载于列车底部[2]），因此动车组的高速运行使得变压器长期经受频繁的机械振动[3]，这使得车载变压器绕组移位的风险显著上升。如若未及时检测出绕组移位故障，并开展相关检修工作，随着运营里程的增加绕组的累积移位将显著增加，会影响到车载变压器乃至动车组的安全稳定运行，因此绕组状态的高效准确检测至关重要。

变压器绕组常规的检测方法包括2大类：在线检测方法与离线检测方法。振动法是最常见的在线检测方法，优势在于检测时不影响变压器正常运行，缺点在于针对特定绕组故障的灵敏度有限[4−5]。短路阻抗法和频率响应法是使用较为广泛的离线检测方法[6−7]，其中短路阻抗法由于评判指标简单直观，方便比较，在现场工程检修中得到广泛应用，不过缺点在于无法提供足够的特征信息用于进一步研究，因此仅能够用于初步诊断变压器状态。相比于上述方法，频率响应法作为一种成熟的绕组状态评估方法得到广泛应用，即通过在变压器绕组一端施加正弦扫频信号，在另一端测量响应信号，通过计算得到幅相曲线作为该方法状态评估的依据。为了建立变压器绕组状态的差异化与幅相曲线的关联性，国内外学者开展了大量研究，同时形成了一系列标准可供现场参考[8−10]。

华北电力大学和西南交通大学的学者分别建立了改进型的传输线模型和集总参数电路模型[11−12]，可用于模拟各种频率响应曲线。澳大利亚的学者开展了绕组故障与等效电路参数的关联性研究，为故障诊断奠定理论基础[13−14]。然而以上研究在绕组故障诊断中单纯依据工程人员分析曲线的变化规律，这种经验分析法的主观性较大，无法推广应用。为此，需要进一步提取曲线的更多特征，用于提高故障诊断的准确性。现有研究将曲线转化为多个维度（包括二值化图像、传递函数和极坐标图），借此可以提供更多的特征信息用于开展进一步分析，例如：二值化图像的质心偏移可用于区分故障位置[15]，传递函数的W指数可实现故障程度的判定[16]，极坐标图的纹理特征可用于区分故障类型[17]。联合上述特征参量与人工智能算法，可以实现绕组故障的智能识别，将极大地提高故障诊断的准确性[18−21]。相比于陆地变压器，高速铁路动车组车载变压器采用分裂式绕组结构，4组绕组在油箱内部并联连接。现有研究中频率响应分析（FRA）仿真模型和诊断方法无法直接适用于该类变压器，难以实现绕组状态评估以及确定故障位置，这影响了故障诊断的准确性。

本文针对高速铁路动车组车载变压器，联合MATLAB软件与Maxwell软件，考虑相间电容参数矩阵，建立频率响应优化模型，并通过实际测试与仿真曲线的对比验证建模方法的有效性；在此基础上，针对车载变压器特殊绕组结构提出了一种故障定位方法，联合多端口测试数据判定故障位置并基于优化模型完成验证。

1 车载变压器频率响应优化模型

1.1 绕组结构

针对高速铁路动车组车载变压器开展研究，型号为JQDFP-6300/25。变压器额定容量为6 300 kV·A，变比为25 kV∶1.8 kV。动车组动力系统要求车载变压器的高压绕组对牵引绕组的阻抗电压为21%。为满足该要求，高压绕组和牵引绕组采用分裂式绕组结构，分为结构高度完全对称的4组绕组，其中牵引绕组处于内侧，高压绕组处于外侧。为了满足差异化牵引负载，每组牵引绕组分别引出接线端子和套管相连接；与此同时，为了有效减小套管数量、降低变压器油箱体积，4组高压绕组采用并联结构，仅有2个接线端子与接触网连接。绕组结构中，铁芯为硅钢片堆叠结构；高压绕组为饼式结构，包含44个线饼，共计1 135匝；牵引绕组为双层层式结构，包含84匝。

车载变压器绕组结构如图1所示。图中：HVi为第i组绕组中的高压绕组（i=1，2，3，4，）；Ti−j为第i组绕组中第j层的牵引绕组（j=1，2）；A和X为高压绕组引出线端口，与接触网连接；ai和xi分别为第i组绕组中牵引绕组外层和内层的引出线端口。

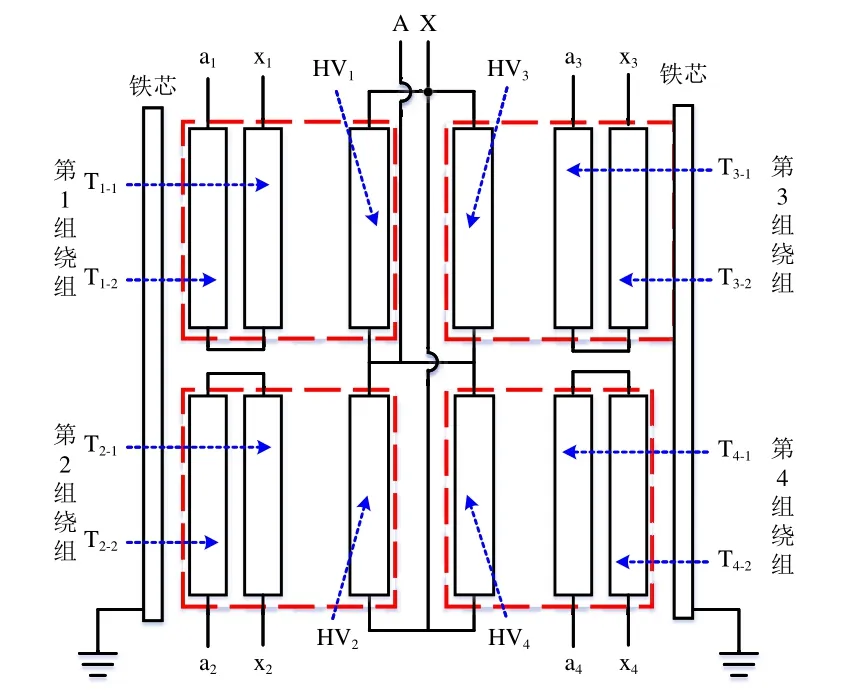
图1 车载变压器绕组结构图

根据相关标准（DL/T 911—2016，IEEE std C57.149—2012 和 IEC 60076—2018） 可 知[8−10]：在待检测绕组的一端注入正弦扫频信号的电压为Uin，在另一端口测量输出信号的电压为Uout，则得到的激励信号与响应信号的传递函数H(f)为

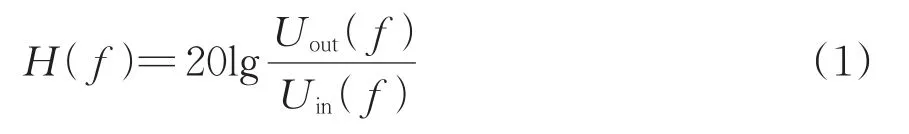
式中：H(f)为频域下输出信号与扫频信号的比值；f为正弦扫频信号的频率。

然而，车载变压器的4组高压绕组在油箱内部并联连接，无法实现每组绕组的独立测试。同时，4组高压绕组在机械结构上完全一致，空间位置完全对称。单纯依靠A-X端口的测试结果无法实现高压绕组的故障定位。有必要探究高压绕组差异化故障位置下所有端口的频率响应分析（FRA）曲线变化规律，总结出故障绕组的定位方法。

1.2 集总参数电路

频率响应测试下变压器绕组可以等效为由电阻、电容、电感元件组成的集总参数电路，该电路是频率响应模型的物理表达。目前常规研究方法为采用电路仿真软件（例如Multisim和ATP/EMTP）搭建电路进行模拟研究[13]。由于车载变压器结构上的对称性，采用MATLAB软件选择第1组绕组作为研究对象，绘制相应的集总参数电路如图2所示。图中：Ct和Gt分别为并联电容和并联电导；Cg和Gg分别为对地电容和对地电导；Ck和Gk分别为相间电容和相间电导；Rs为单位长度电阻；L为自感；M为互感。

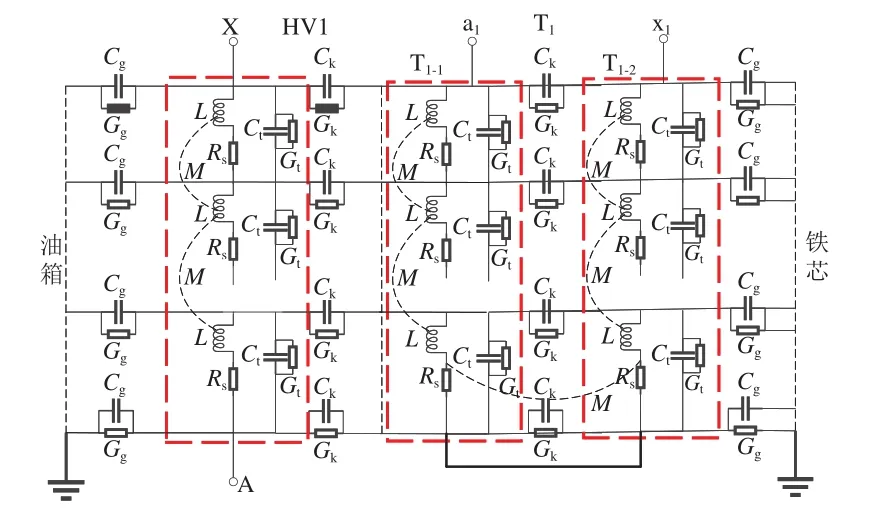
图2 车载变压器第1组绕组的集总参数电路

相较于陆地变压器，车载变压器的结构更为复杂，高压绕组与牵引绕组的相间电容与电感无法在仿真软件中全部考虑到。为了能够建立精细化电路模型，准确模拟不同故障位置下频率响应曲线，定义高压绕组与牵引绕组的单饼（匝）为1个电路单元。

1.3 参数求解

联合有限元法与公式法计算图2集总参数电路模型中的电气参数。为此在Maxwell软件中按照实际尺寸建立车载变压器的三维有限元模型，并与实物对比，如图3所示。

图3 车载变压器仿真模型与实物对比

根据国内外相关研究可知：绕组及铁芯相关支撑结构件（铁芯夹件、线圈垫块）对于电气参数没有影响[11]，为了节约计算资源、提高计算效率，在仿真软件中忽略了这些相关支撑结构件。

1）电感参数

在Maxwell软件中静磁场求解电感参数，利用麦克斯韦方程提取电感矩阵，得第m个电路单元的自感Lmm和绕组的第m个电路单元与第n个电路单元间的互感Mmn为

式中：Wmm为第1个绕组的从上至下第m个电路单元自身激发的磁能；WL−mn为电流Im和In分别作用于绕组的第m个电路单元和第n个电路单元时的磁场能量。

2）电容参数

在Maxwell软件中静电场求解电容参数，利用麦克斯韦方程组求解电容矩阵。根据能量平衡关系计算绕组第m个电路单元与第n个电路单元间的电容Cmn为

式中：Umn为绕组的第m个电路单元与第n个电路单元间的电压；WC−mn为电压Umn作用于绕组的第m个电路单元和第n个电路单元时的电场能量。

3）电导参数

在求解电容参数的基础上，电导参数可以由并联电容和介质损耗角（tanδ）计算。为了精确计算，考虑了tanδ与激励频率f的关系得到电导G为

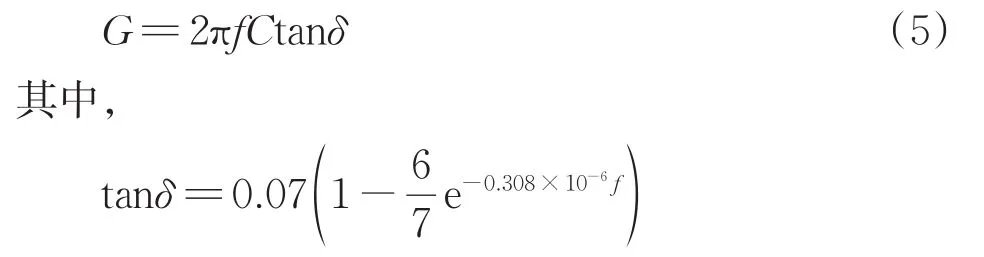
4）电阻参数

电阻和导线长度紧密相关，为此计算单位长度导线的电阻。考虑到集肤效应，单位长度电阻Rs为

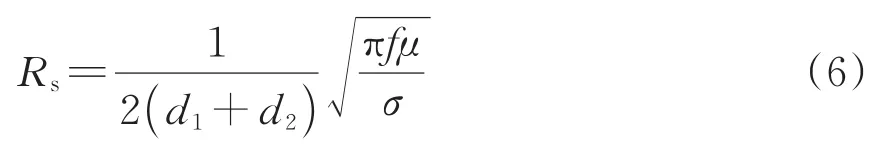
式中：d1和d2分别为矩形导体横截面的高度和宽度；μ为导体磁导率；σ为导体电导率。

1.4 参数优化

在对传统频率响应模型参数求解时未考虑不同绕组的全部相间电容，仅考虑相邻电路单元间电容会使仿真精度明显下降，因此在改进传统频率响应模型时应考虑同一铁芯上电路单元间全部相间电容。以第1组绕组为例，高压绕组与牵引绕组的相间电容如图4所示。图中：n1为高压绕组的电路单元数量；n2为牵引绕组T1−1的电路单元数量；n3为牵引绕组T1−2的电路单元数量。由图4可见：高压绕组HV1的每个电路单元与牵引绕组T1−1的每个电路单元间的相间电容均有考虑；同理，牵引绕组T1−1与T1−2的电路单元相间电容也做类似处理。

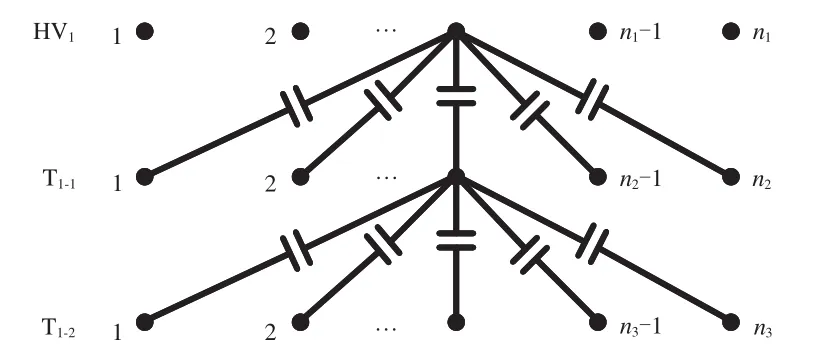
图4 基于第1组绕组的改进型电容参数示意图

根据图4中改进型电容参数示意图，得到电容矩阵C为

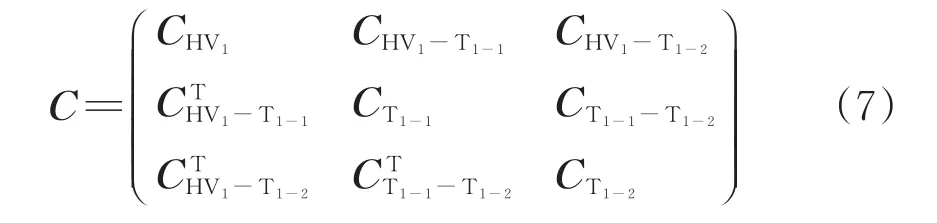
式中：CHV1−T1−1为高压绕组 HV1与牵引绕组 T1−1间的相电容矩阵；CHV1−T1−2为高压绕组HV1与牵引绕组T1−2间的相电容矩阵；CT1−1−T1−2为牵引绕组 T1−1与牵引绕组T1−2间的相电容矩阵；CHV1为高压绕组HV1的自身电容系数矩阵；CT1−1为牵引绕组 T1−1的自身电容系数矩阵；CT1−2为牵引绕组T1−2的自身电容系数矩阵。这些电容均使用式（4）计算得到。

1.5 状态空间方程推导

基于1.2节、1.3节和1.4节建立变压器绕组频率响应优化模型，且模型中参数均准确求解。在此基础上，在MATLAB软件中推导求解状态空间方程，即电路任一端口注入激励（正弦扫频信号），求解其他任一端口的响应信号，进一步求解输入信号与输出信号的传递函数及其频率响应曲线表达式。

选取每个电路单元的节点电压Ui和电流Ii作为状态变量，使用基尔霍夫电压与电流关系建立每个电路单元的节点电压与电流之间的关系为

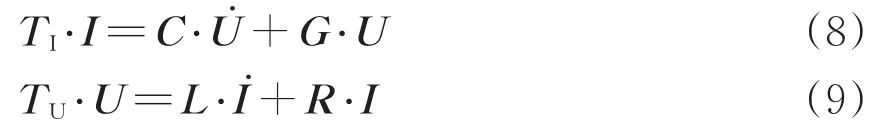
其中，

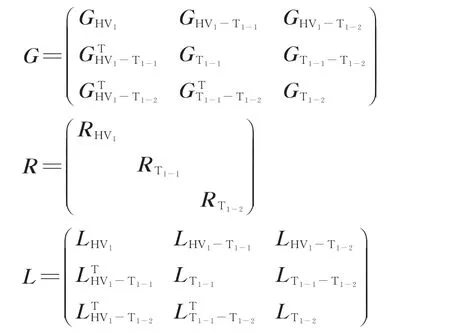
式中：U和I分别为电压矩阵与电流矩阵；U̇和İ分别为U和I对时间的导数；TI和TU分别为电流系数矩阵和电压系数矩阵；R，L，C，G分别为电阻、电感、电容与电导的系数矩阵；RHV1为高压绕组HV1的自身电阻系数矩阵；RT1−1为牵引绕组 T1−1的自身电阻系数矩阵；RT1−2为牵引绕组T1−2的自身电阻系数矩阵；GHV1−T1−1为高压绕组 HV1与牵引绕组T1−1间的相电导矩阵；GHV1−T1−2为高压绕组HV1与牵引绕组 T1−2间的相电导矩阵；GT1−1−T1−2为牵引绕组T1−1与牵引绕组T1−2间的相电导矩阵；GHV1为高压绕组HV1的自身电导系数矩阵；GT1−1为牵引绕组T1−1的自身电导系数矩阵；GT1−2为牵引绕组 T1−2的自身电导系数矩阵；LHV1−T1−1为高压绕组HV1与牵引绕组 T1−1间的相电感矩阵；LHV1−T1−2为高压绕组HV1与牵引绕组 T1−2间的相电感矩阵；LT1−1−T1−2为牵引绕组T1−1与牵引绕组T1−2间的相电感矩阵；LHV1为高压绕组HV1的自身电感系数矩阵；LT1−1为牵引绕组T1−1的自身电感系数矩阵；LT1−2为牵引绕组T1−2的自身电感系数矩阵。

当外部激励信号（Uin）作用于节点k时，式（8）和式（9）可以改写为

式中：W为不含第k行的矩阵CT；J为矩阵TU的第k列；TI'为不含第k行的矩阵TI；为不含第k列的矩阵TU。

合并式（10）与式（11），将状态空间方程变换为

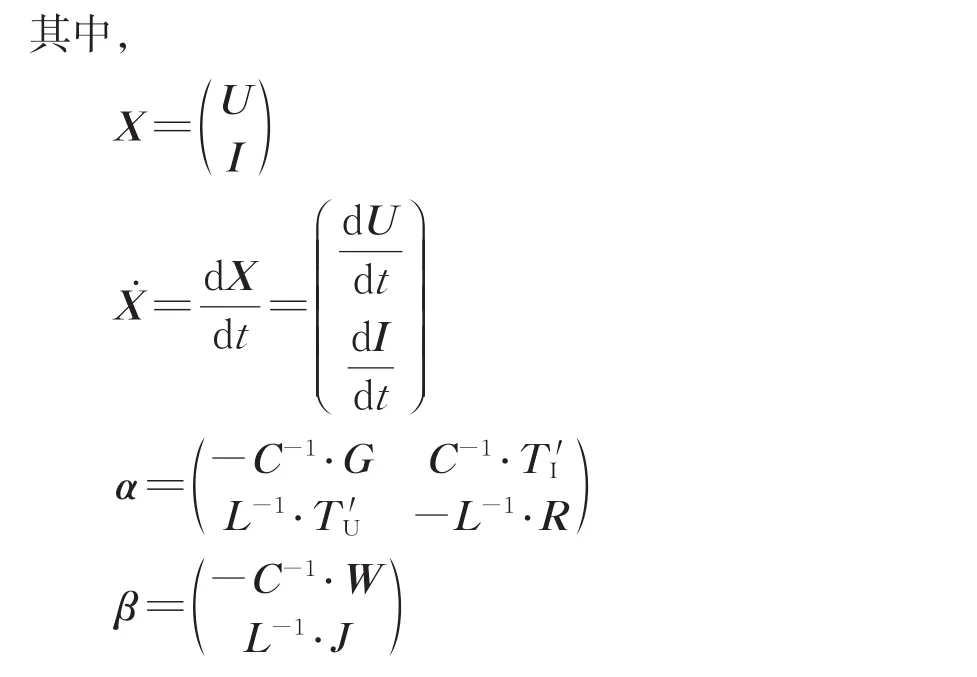
式（12）转换到频域即可得到集总参数电路中各电路单元节点电压和电流对激励信号（Uin）的传递函数为

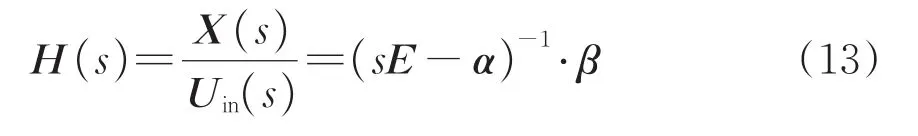
式中：E为单位矩阵；s为拉普拉斯算子。

1.6 模型验证

为了验证车载变压器频率响应优化模型的正确性，开展频率响应测试，如图5所示。选择的测试设备为频率响应分析仪，主要参数为：激励频带为1 kHz～1 MHz；采样率为 100 MHz·s−1；设备阻抗与采样阻抗为50 Ω；测量电压峰值为10 V。

图5 车载变压器频率响应法现场测试

由于车载变压器结构的对称性，选择第1组绕组作为测试对象开展相关研究。采用输入与输出电压比作为变压器频率响应的测量对象。车载变压器频率响应测试接线原理如图6所示。试验时，选择A-X与a1-x1作为2组测量端口。在A端注入1个频率为f、电压为Uin的正弦扫频信号，在X端采集输出信号的电压Uout。同理，在a1端注入同样的正弦扫频信号，在x1端采集输出信号。

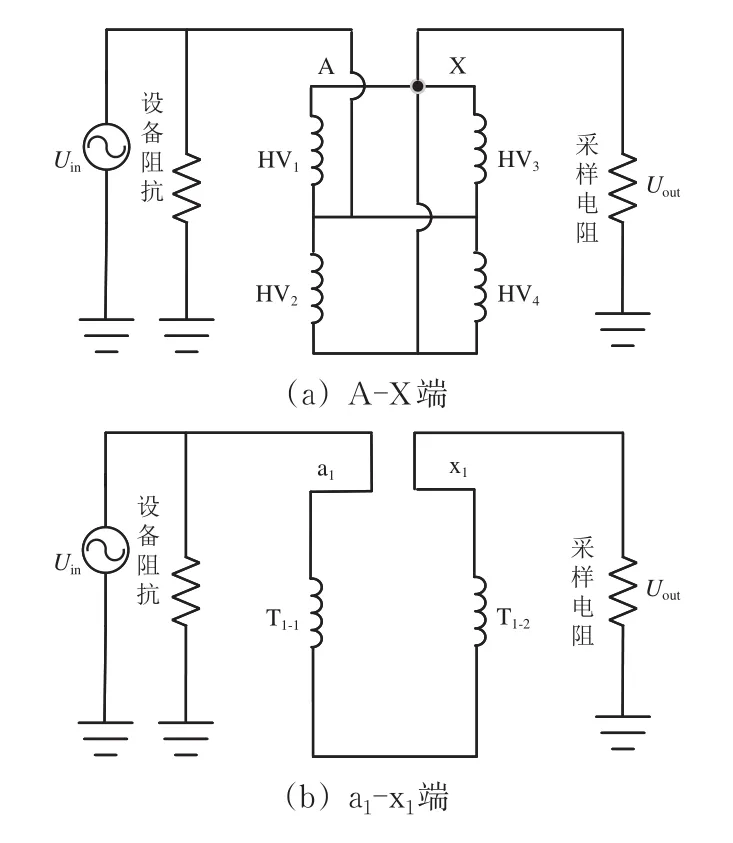
图6 车载变压器频率响应测试接线原理

试验得到车载变压器不同端口的仿真曲线与实测曲线对比如图7所示。

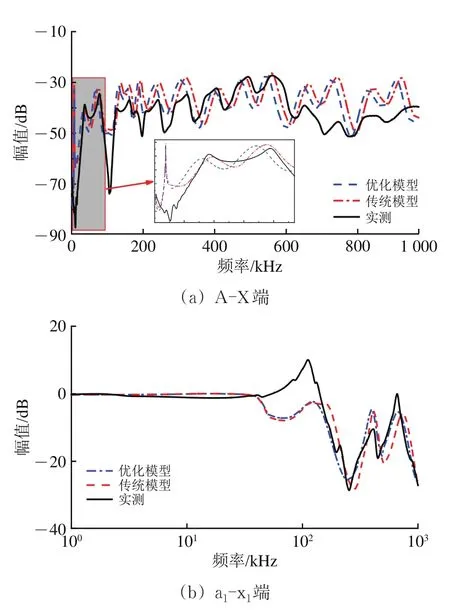
图7 频率响应曲线仿真与实际测试对比

由图7可见：相比于传统模型，优化模型在谐振点上均表现出较高的准确性；优化模型曲线与实测曲线的相似程度较高，尽管各个谐振点的幅值存在小幅偏差，但是谐振频率基本吻合。依据现有研究可知，仿真与实测的差异主要是因为变压器实际生产加工过程中，受到工程人员加工等不可控因素影响，使得每台变压器样本在结构上存在小幅差异，这种结构偏差主要体现在曲线的高频段差异。图7中，曲线的高频段幅值偏差略微增加，其误差均在允许范围内，与现有研究吻合。

综上可知：改进的建模方法能够准确模拟车载变压器的FRA曲线。

2 基于优化模型的故障定位步骤

根据标准IEEE Std C57.149—2012及IEC 60076—2018可知：同一芯柱上的线圈会互相影响彼此FRA曲线。相比陆地变压器，车载变压器的轴向油道宽度更小，相间电磁耦合效应更加显著，这会加剧同一芯柱上高压线圈与牵引线圈的互相影响。为了定量计算高压绕组与牵引绕组的电磁耦合效应，使用1.3节的方法计算高压绕组与牵引绕组不同位置线饼的等效电容参数，结果见表1。由于牵引绕组采用层式结构，纵向等值电容Ct为0，相间电容Ck明显大于对地电容Cg，因此牵引绕组ai-xi端口FRA曲线主要受到相间电容的影响。与此同时，高压绕组发生故障时高压绕组与牵引绕组的相间电容变化显著。综合上述分析可知：高压绕组故障使得同一组牵引绕组的测试端口ai-xi的FRA曲线相应改变。结合高压绕组测试端口A-X与各个牵引绕组测试端口ai-xi实现故障绕组定位。

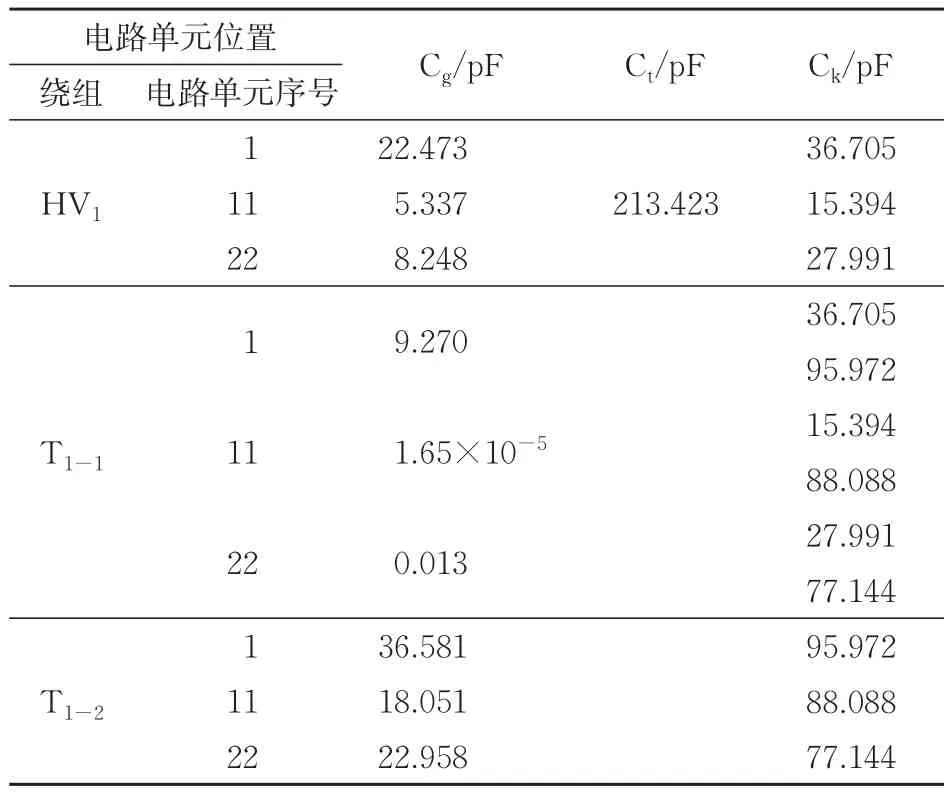
表1 集总参数电路模型-电容参数

由于牵引绕组靠近铁芯，依据中国电力行业标准DL/T 911—2016，低频激励下绕组感抗大、容抗小、容抗作用不明显，这导致图7（b）FRA曲线在30 kHz及以下频段不存在谐振点。随着激励频率的增加，电容参数的影响变大，导致谐振点数量增加。当变压器绕组发生故障时，集总参数电路主要表现为电容参数变化，谐振点的幅值与频率相应变化，因此针对谐振幅值与谐振频率的变化规律开展研究。

在2.1节理论分析的基础上，针对特殊结构的车载变压器，提出了多端口FRA曲线分析方法，用于实现车载变压器绕组故障定位。该方法如图8所示，具体步骤如下。

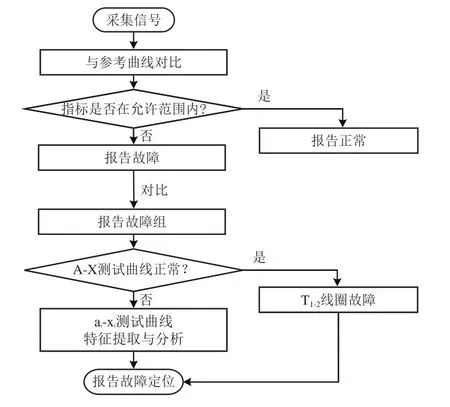
图8 车载变压器故障定位流程图

步骤1：测试高压绕组与牵引绕组的端口FRA曲线，包括A-X端口与ai-xi端口2种测试方式。

步骤2：依据中国电力行业标准DL/T 911—2016，依次计算待检测曲线的低频段（1～100 kHz）、中频段（100～600 kHz）及高频段（600～1 000 kHz）的相关系数，分别为

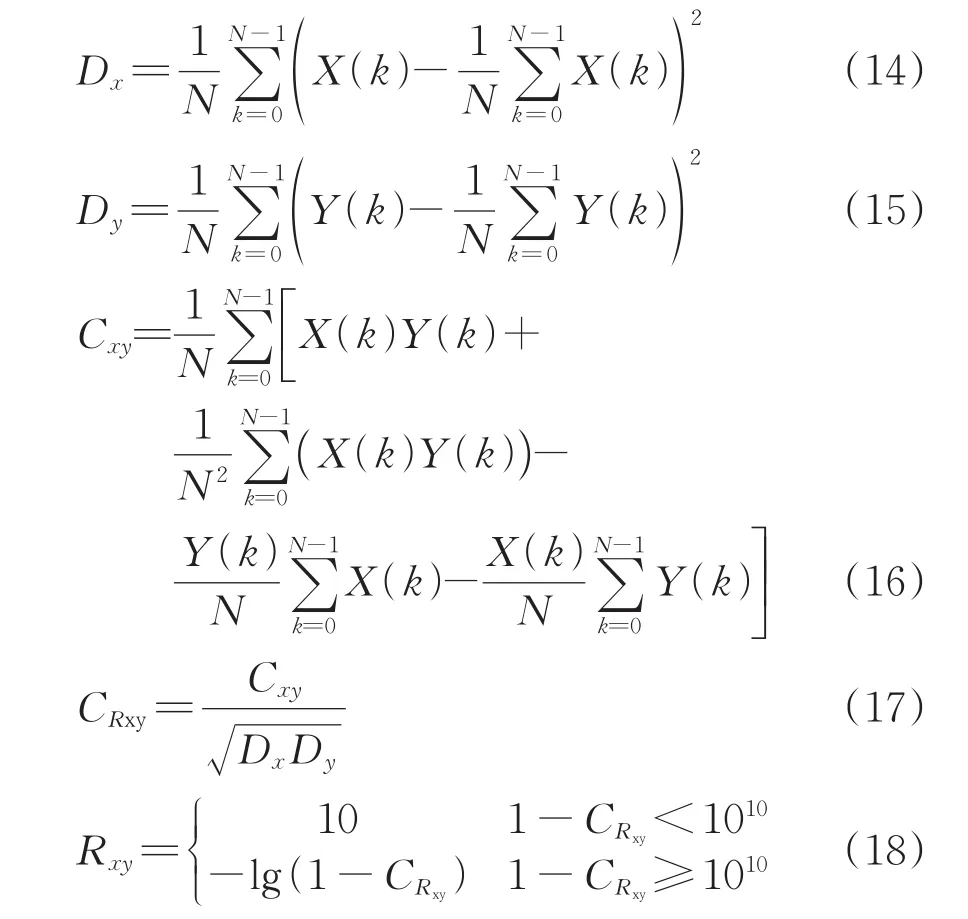
式中：X（k）和Y（k）分别为长度为N的参考曲线与待检测曲线的幅值序列，幅值序列的自变量k的取值范围是0，1，…，N-1，且X（k） 和Y（k） 均为实数；Dx为幅值序列X（k）的标准方差；Dy为幅值序列Y（k）的标准方差；Cxy为幅值序列X（k）与Y（k）的协方差；CRxy为幅值序列X（k）与Y（k）的归一化协方差系数；Rxy为幅值序列X（k）与Y（k）的相关系数。

针对A-X端口与a1-x1端口的FRA曲线分频段计算待检测曲线与参考曲线的相关系数。为分析车载变压器状态，须依据DL/T 911—2016的相关系数区间，见表2。表中：RLF为曲线在低频段的相关系数；RMF为曲线在中频段的相关系数；RHF为曲线在高频段的相关系数。

表2 相关系数与变形程度的关系

（1）当相关系数Rxy均处于正常区间时，即绕组均处于正常状态，完成状态评估。

（2）当任意端口的测试数据显示相关系数处于故障区间，即表明变压器绕组存在故障，进入步骤3开展进一步故障定位研究。

步骤3：如若待检测数据的相关系数表明变压器处于故障状态，在此基础上对比4个端口（a1-x1，a2-x2，a3-x3和a4-x4）的频率响应测试曲线。任一曲线相比于参考曲线存在显著差异，即表明端口所在的该组线圈存在故障，判定故障发生在第i组绕组。

步骤4：在明确故障绕组组别的基础上，进一步分析A-X端口的FRA曲线。（为了进一步故障定位的方便，假定故障发生在第1组绕组，以此为例开展详细说明）

（1）若A-X端口FRA曲线几乎不发生明显改变，即表明故障位于牵引绕组T1−2，完成故障定位（因为牵引绕组T1−2处于最内侧，而且与高压绕组HV1中间间隔牵引绕组T1−1。因此，牵引绕组T1−2发生故障时，对于A-X端口的FRA曲线影响可以忽略）。

（2）若曲线发生明显改变，即表明故障位于高压绕组HV1和牵引绕组T1−1，进入步骤5进行下一步区分（因为故障发生在上述位置下，高压绕组与牵引绕组的相间电容会发生明显改变）。

步骤5：分析a1-x1端口的FRA曲线。高压绕组HV1故障与牵引绕组T1−2故障下等效电路参数变化规律存在明显差异。高压绕组HV1故障下对地电容Cg和相间电容均会发生明显改变；T1−1故障下相间电容发生显著变化。不同的参数变化会使得a1-x1端口的FRA曲线变化趋势存在明显差异。结合2.1节的理论分析，牵引绕组端口的FRA曲线谐振点变化可作为故障定位依据。

3 故障定位验证

3.1 故障模拟

受限于动车组狭小的空间，车载变压器的4组绕组水平装载于油箱内，如图9所示。在重力作用下，高速运行中动车组自身的机械振动频繁，车载变压器绕组沿轴向发生移位的风险较大。同时车载变压器返厂检修记录与理论分析一致表明：轴向移位（AD）是车载变压器的常见故障。以AD故障为例，模拟不同故障位置车载变压器不同端口的FRA曲线，进一步验证故障定位方法可行性。

图9 车载变压器空间位置

由于车载变压器结构的对称性，选择第1组绕组作为研究对象，即针对高压绕组HV1、牵引绕组T1−1和T1−2设置轴向移位。轴向移位故障的原理如图10所示。图中：黑色框表示移位前位置，红色框表示移位后位置。

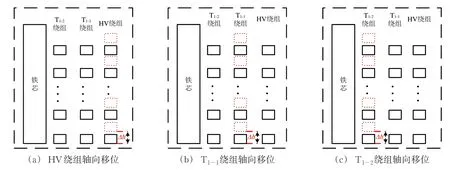
图10 轴向移位原理图

将移位距离作为故障模拟标准，移位故障程度Δ与绕组高度h、移位距离Δh的关系为

模拟验证时，因车载变压器绕组高度h为425 mm，将移位故障程度分别设置为1%，2%和3%，根据式（19）得到移位距离，可分别模拟高压绕组HV1、牵引绕组 T1−1和 T1−2发生的移位故障，并包含A-X与a1-x1这2种接线方式，共计20条频率响应曲线。

3.2 牵引绕组T1-2故障定位

依据上文所述车载变压器故障定位方法，针对不同故障位置的FRA曲线开展研究。采用反向验证的方式，将已知故障位置的FRA曲线输入图8所示的流程图进行分析判断，对比实际故障位置与理论定位结果验证方法的正确性。

步骤1：当牵引绕组T1−2发生不同程度的轴向移位故障时，A-X端口与a1-x1端口的FRA曲线变化分别如图11所示。

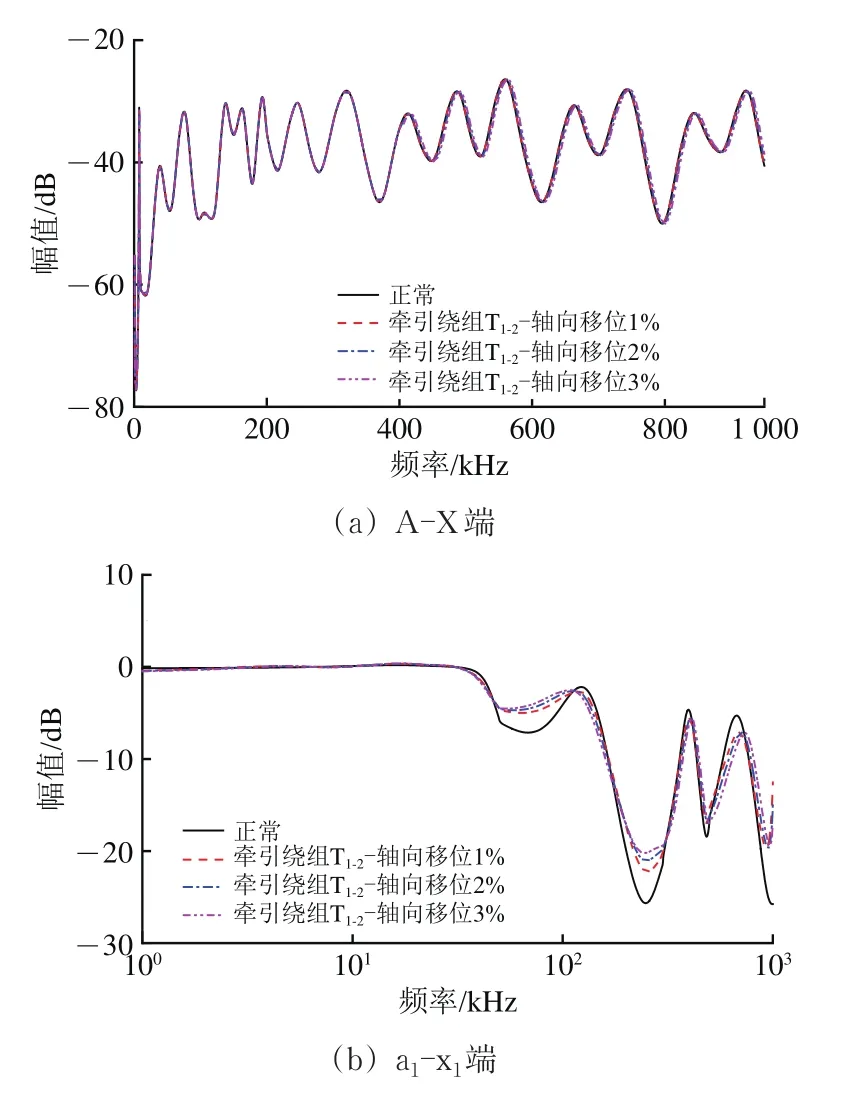
图11 牵引绕组T1-2故障下频率响应曲线

步骤2：计算出曲线在不同频段的相关系数，结果见表3。由表3可知：相较于参考曲线，A-X端口的FRA曲线不发生明显改变；a1-x1端口的FRA曲线变化较为显著。即表明变压器绕组处于故障状态。

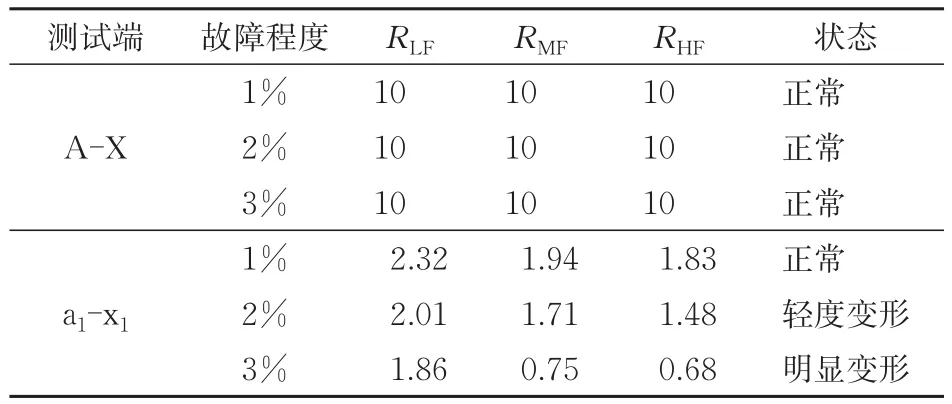
表3 牵引绕组T1-2不同故障程度下的相关系数

步骤3：类比a1-x1端口与其他3个端口的FRA曲线，表明了故障发生在变压器第1组绕组。

步骤4：A-X端口的FRA曲线在各个频段的相关系数均处于正常范围，即表明FRA曲线属于正常。综合以上数据分析可知：变压器绕组的故障定位在牵引绕组T1−2。该规律与2.2节中的理论分析保持较高一致性，验证了牵引绕组T1−2故障定位的准确性。

3.3 牵引绕组T1-1与高压绕组HV1的故障定位

步骤1：当高压绕组HV1和牵引绕组T1−1发生轴向移位时，A-X端口与a1-x1端口的FRA曲线变化分别如图12和图13所示。

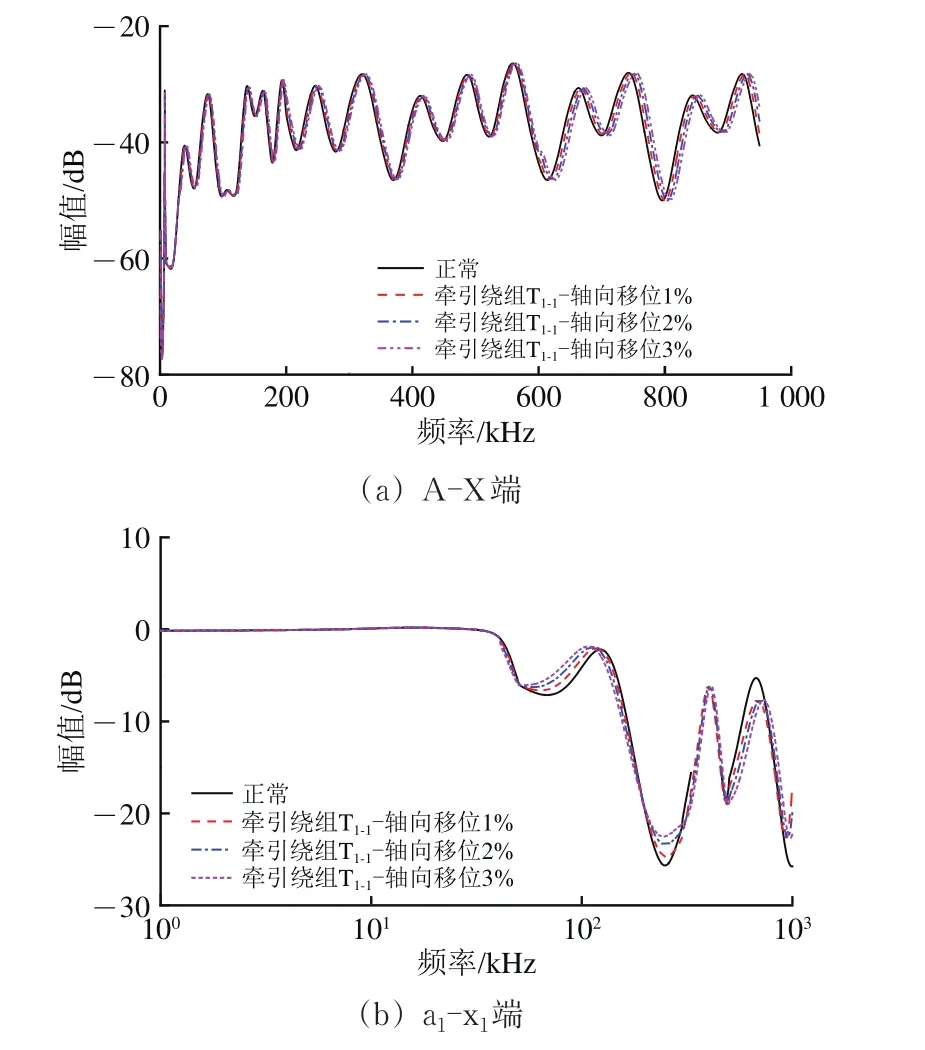
图12 牵引绕组T1-1故障下频率响应曲线

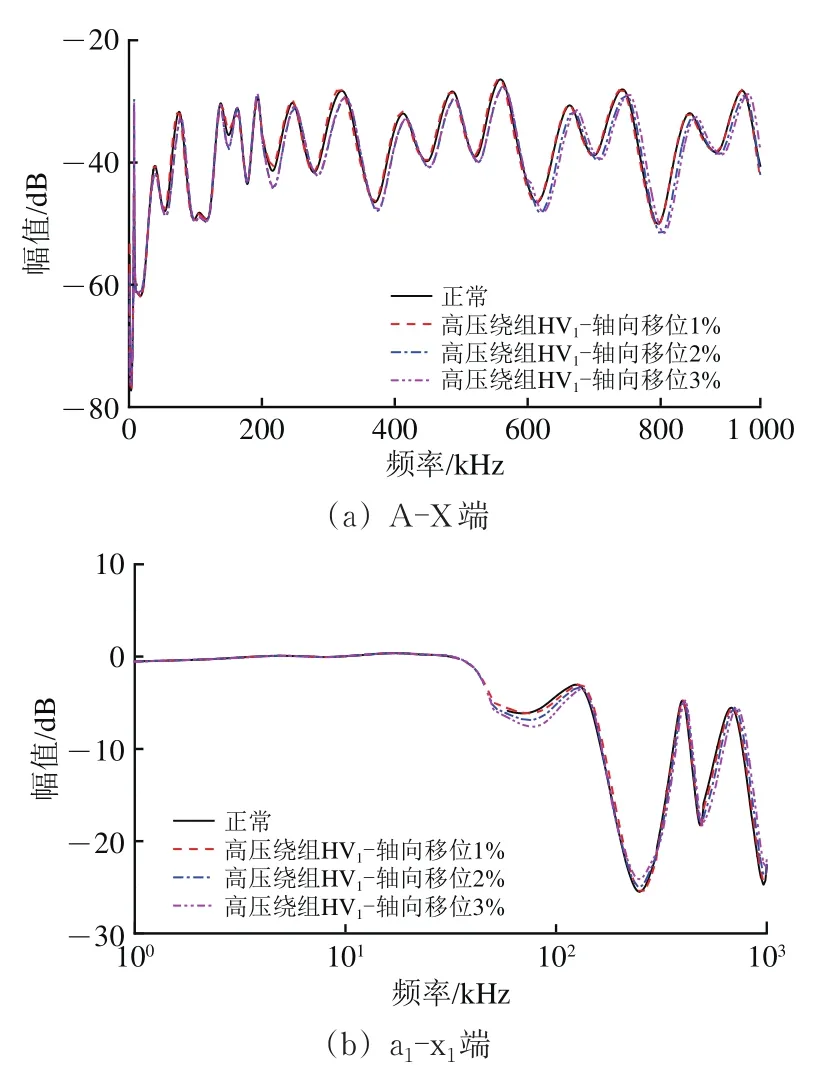
图13 高压绕组HV1故障下频率响应曲线

步骤2：计算出高压绕组HV1和牵引绕组T1−1的频率响应曲线在不同频段的相关系数，结果分别见表4和表5。由表4和表5可知：相较于参考曲线，A-X端口和a1-x1端口的测试曲线变化较为显著，即表明变压器绕组处于故障状态。

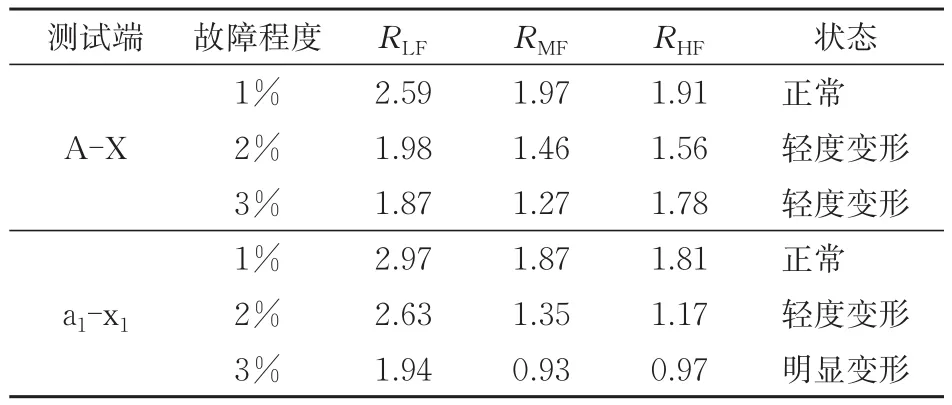
表4 牵引绕组T1-1不同故障程度下的相关系数

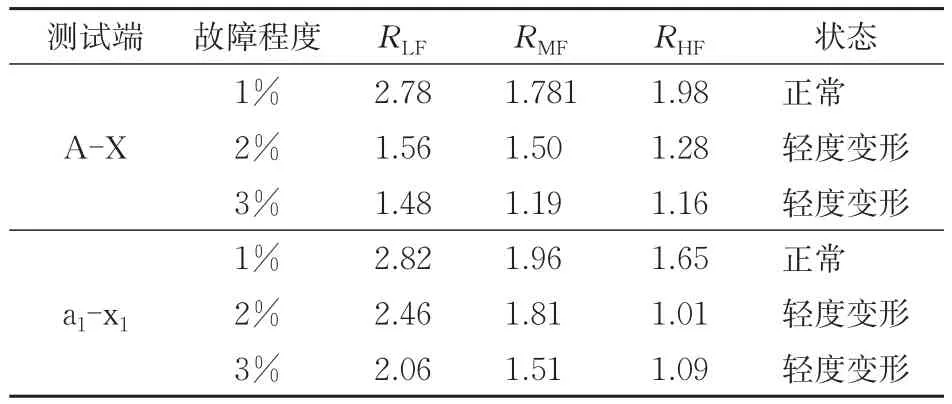
表5 高压绕组HV1不同故障程度下的相关系数

步骤3：类比a1-x1端口与其他3个端口的测试曲线，表明了故障发生在变压器第1组绕组上。

步骤4：由于A-X端口和a1-x1端口的FRA曲线均发生显著变化，即可判定故障绕组为高压绕组HV1和牵引绕组T1−1。

步骤5：依据2.2节中介绍的方法，选择a1-x1端口的FRA曲线第一谐振点、第二谐振点与第三谐振点作为特征点开展进一步研究。为了定量描述曲线的变化，总结不同状态下谐振频率的变化规律见表6。由表6可知：高压绕组HV1和牵引绕组T1−1故障下，第一谐振点与第二谐振点的频率偏移方向完全相反；同时，高压绕组HV1故障对第三谐振点的谐振频率几乎不产生影响，而牵引绕组T1−1故障下第三谐振点谐振频率的偏移程度与故障程度正相关。上述分析表明，特征谐振点可用于区分高压绕组HV1和牵引绕组T1−1的故障。

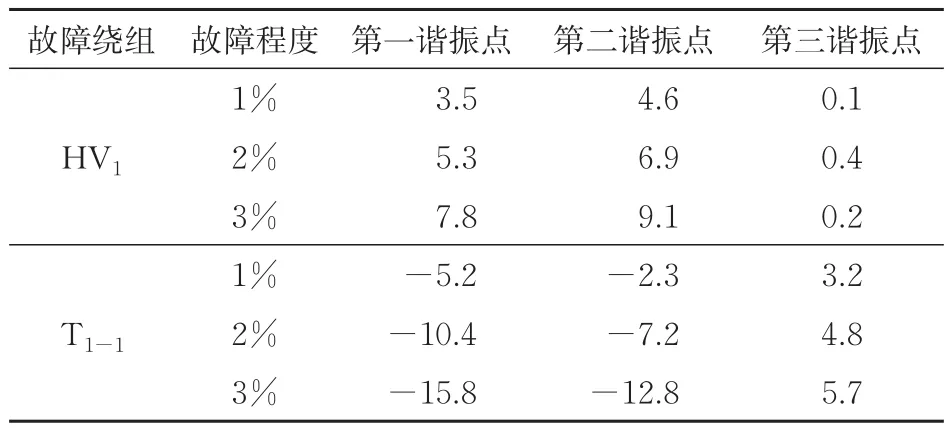
表6 不同故障位置特征谐振点-谐振频率偏移

4 结 论

（1）建立了考虑绕组相间电容的车载变压器频率响应优化模型，相比于传统模型，优化模型具有更高的测试精度，谐振频率不存在显著偏差。基于优化模型可以用于准确模拟差异化状态下车载变压器各端口的频率响应曲线。

（2）提出的定位方法是根据A-X端口与a1-x1端口的频率响应曲线变化规律实现故障位置的确定：以第1组绕组为例，牵引绕组T1−2发生故障下，A-X端口的FRA曲线不发生变化，a1-x1端口的FRA曲线变化显著。其他故障位置下，A-X端口的FRA曲线均发生明显改变。结合a1-x1端口的FRA曲线的特征谐振点可实现牵引绕组T1−1和高压绕组HV1的故障位置区分：第一谐振点与第二谐振点的频率偏移方向完全相反。同时HV1故障对第三谐振点的谐振频率几乎不产生影响。