基于因子图导航的伪距故障检测与自适应隔离方法

孙克诚，曾庆化，王守一，刘建业，黄 艳

（南京航空航天大学 导航研究中心，南京 210016）

可靠的导航和定位能力是无人系统的主要属性。无人系统的导航状态通常是通过融合自惯性导航系统（Inertial Navigation System,INS）和全球导航卫星系统（Global Navigation Satellite System,GNSS）测量的多传感器信息进行估计的[1]。由于外界干扰或震荡的环境，传感器容易出现误差增大甚至故障的情况。震荡环境会使得惯性导航系统解算错误，误差突然增加，甚至出现解算故障[2,3]。全球导航卫星系统信号更容易受到电磁干扰，在城市环境、隧道及其他未知恶劣环境下，全球导航卫星系统的定位精度较差，这些区域的GNSS 信号接收受到干扰，甚至接收不到信号[4,5]。因此，有效的故障检测和隔离方法以及在未知干扰下的鲁棒导航对安全至关重要。

考虑到复杂环境的影响下传感器的不可预测性能变化，传统的滤波算法难以满足鲁棒性的要求。而因子图的优势是其出色的即插即用能力，以灵活的结构[6,7]处理异步和即插即用问题。1981年，Tanner[8]引入了一个二部图描述低密度奇偶校验码的奇偶校验矩阵，称为“Tanner 图”。文献[9]基于Tanner 图、Wiberg图和其他模型提出了因子图概念和和积算法。文献[10]详细地将卡尔曼滤波、最小二乘法与基于因子图的和积算法结合，并通过因子图模型描述了估计算法。文献[11]提出了一种基于因子图的惯性/视觉信息融合方法，将信息融合问题表示为因子图模型。文献[12]使用增量平滑和映射优化了全局因子图中的关键帧。文献[13]提出了一种改进的因子图多传感器融合导航算法，实现了无人机多源导航系统方法。文献[14]提出了基于因子图的AUV 多传感器组合导航算法，有效实现惯性导航系统与不同导航传感器的非等间隔融合。文献[15]通过考虑GNSS 伪距误差模型和环境条件，评估了窗口大小对因子图优化性能的影响。文献[5]设计了一个动态权重函数调整每个因子的权重，从而提高了因子图的导航性能和鲁棒性。这些方法在保持图理论即插即用功能的同时，提高了导航性能。因子图的主要特点是抽象子导航系统，实现快速集成、重构和滤波的算法。有效地检测和隔离算法可以帮助快速定位故障传感器，并且隔离掉可能污染整个系统的故障量测。因子图与故障检测和隔离方法相结合可以灵活地实现可靠的导航。

在安全关键应用程序（Safety-Critical Applications,SCA）中，故障检测和隔离（Fault Detection and Isolation,FDI）是一个重要方面，可以防止用户因导航系统中的传感器故障而面临潜在风险[16]。文献[17]提出了一种新的故障检测算法，其中卡尔曼滤波器被多模型算法取代。文献[18]基于残差卡方检验方法设计了一种容错卡尔曼滤波器方案，包括三个子滤波器和一个主卡尔曼滤波器。文献[19]设计了基于观测器的鲁棒传感器故障诊断滤波器，可保证量测残差对于故障及增广扰动具有鲁棒性，残差对于故障及扰动的鲁棒性能指标均小于给定值1.18，具有良好的鲁棒性。文献[20]通过在容错组合导航系统中加入神经网络，提出了一种基于深度神经网络的智能主动容错系统。文献[21]分析了残差卡方的检测性能，并提出了两个合适的阈值计算每个测量的权重因子。文献[22]提出了一种基于AR 量测建模的组合导航系统渐变故障双阈值检测方法，避免由于传统残差c2检测方法因引入观测污染数据,对渐变故障不敏感的问题。文献[2]研究了方差偏移异常值模型，该模型根据方差中相关偏移的大小排除或包含测量值，以检测原始伪距数据中的故障。文献[23]提出了一种传感器验证方法，该方法将基于残差的测试统计数据与Kalman-Schmidt 滤波器的部分更新公式相结合，为传感器模型验证提供可靠的方法，以保护导航系统的完好性。然而，灵活的图优化结构所涉及的故障模式较为多样，尤其是INS节点故障或GNSS 节点伪距故障的问题，目前与之适应的有效故障检测和隔离方法还有待进一步深入研究。

众所周知，GNSS 的量测容易受到电磁环境和遮挡的干扰，伪距中可能包含故障误差。在复杂的道路环境和发动机受到干扰的情况下，载体容易发生振动。INS 是自主系统的核心传感器，复杂的环境变化可能导致其不稳定或电子元件损坏，故障如果没有被及时诊断将会导致严重事故。为了解决复杂环境下导航设备的故障问题，提出了一种基于因子图导航的伪距故障检测与自适应隔离方法(Pseudo-range Fault Detection and Adaptive Isolation,PFDAI)，基于因子图导航的 PFDAI 方法采用卫星伪距故障检测(Pseudo-range Fault Detection,PFD)、自适应隔离和即插即用因子图框架，与传统的FDI 算法相比，该方法可以具体到某个卫星存在伪距误差问题或INS 故障，并在此检测结果的基础上，自适应隔离故障因子节点，该方法在故障下具有更好的导航定位效果。针对卫星伪距中存在的部分软/硬故障，本文所提方法可以辅助导航系统获得更好的故障检测和隔离效果。

1 基于因子图导航的故障检测与隔离系统方案

基于FDI 和因子图的导航系统方案如图1所示。因子图中的各类传感器因子节点可以提供位置、速度、姿态测量，在复杂环境中，由于传感器故障，测量的可用性仍然取决于是否有有效的故障检测和隔离算法。在此基础上，为了保证组合导航的可靠性和精度，结合故障检测和图优化的优点，提出了一种改进的伪距故障检测方法。与以INS 测量值作为参考值检测其他导航系统是否存在故障的传统FDI 方法不同，该方法基于GNSS 原始伪距信息和INS 量测检测故障，可以检测并定位具体故障卫星伪距量测，考虑到系统内各子导航系统同时发生故障的概率较小，若故障检测主滤波器判断系统存在故障，而子滤波器判断伪距量测均无问题的情况下，则可以推断为INS 量测故障，此后可以结合卫星接收机自身完好性算法研究，较好保证导航性能。

图1 基于因子图的故障检测和隔离方案Fig.1 Fault detection and isolation scheme based on factor graph

本文在有效检测伪距故障的基础上，进一步提出了自适应隔离方法。在检测到传感器故障后，算法能够自适应隔离故障传感器的测量信息，保证隔离后定位精度。因子图的即插即用特性有利于根据检测结果自适应隔离故障传感器的测量信息。当传感器无故障时，因子图算法将传感器测量作为因子节点添加到因子图框架中。当传感器故障时，因子图算法将通过不添加因子节点或者添加低权重因子节点从而隔离或降低传感器故障量测的影响，所提算法能够在干扰环境下自适应地融合所有可用的信息提高导航精度。

2 卫星伪距故障检测方法

传感器故障下有效的故障检测与隔离方法对导航系统的鲁棒性至关重要。由于周围环境的影响，一些传感器可能会在短时间内处于非活动状态或出现故障。本文目标是结合所有可用信息判断是否存在传感器故障，基于故障检测结果自适应隔离节点以提高导航精度。

根据图2中的多解分离法（MultipleSolution Separation,MSS）检测算法，对每颗卫星的伪距信息进行分析和判断。首先，该检测方法需要一个主滤波器处理所有可见卫星的伪距数据，主滤波器与传统卡方检测方法近似，区别在于传统卡方校验采用位置作为检测依据，伪距检测方法将所有卫星的伪距与惯性导航推算的伪距作为量测值，导航系统位置、速度、姿态和伪距、伪距率为状态值进行故障检测。主滤波器一直保持工作，用于检测导航系统中的突变故障和缓变故障。此外，在主滤波器检测到故障后，代表整体系统存在故障，则启用N个子滤波器，在依次移除一颗可见卫星量测后，剩余所有其他卫星的伪距测量值作为判断依据进入每个子滤波器。如果扣除一颗卫星伪距量测的每个子滤波器依然全部判断存在故障，这意味着不止一颗卫星的伪距存在故障，则每个滤波器再减去一颗卫星的伪距测量值，并将其输入子-子滤波器进行故障判断，以此类推。当所有子滤波器判断存在故障，则判定INS量测基准存在故障。伪距故障检测方法的滤波器结构图如图2所示。

图2 伪距故障检测检测滤波器示意图Fig.2 Structurediagram of thepseudo-range fault detection

对于上述每个子滤波器，基于相应的故障算法构造统计模型。在时间k，对于主滤波器和子滤波器，主滤波器F00使用N个可用的卫星伪距测量计算故障检测校验值的主要滤波估计。在主滤波器中检测到故障后，子滤波器故障检测校验估计值由N个子滤波器（表示为{F0n}nÎ[1,N]）计算。子滤波器F0n根据除第nth颗卫星伪距外的所有卫星伪距测量值检测故障。如果第nth颗卫星出现故障，除第nth滤波器外，其他滤波器的检测值都会受到故障卫星测量的污染，导致检测出故障，而第nth滤波器检测不出故障。因此对比主滤波器和子滤波器的检测校验结果，则可以判断哪颗星的伪距存在故障，表示为：

位置、速度、姿态、接收机时钟偏置误差和接收机时钟误差变化率在故障检测中都非常重要。本文关注11维状态值，其协方差矩阵为）。

通过应用以下假设检验检测故障：

当无故障时，服从高斯概率分布，它的检测特性幅值，服从瑞利分布。其中D0n是一个检测门限，根据内曼-皮尔逊准则，即：

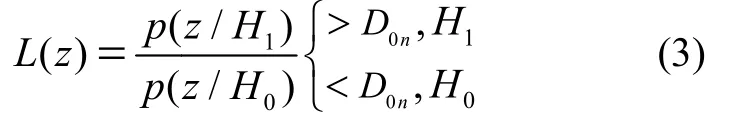
其中z为观测值，L(z)为似然比，D0n称为似然比门限，似然比L(z)在H0为真的条件下的概率密度为p(L/H0)，则由：

就可求解出D0n，D0n满足如下要求：

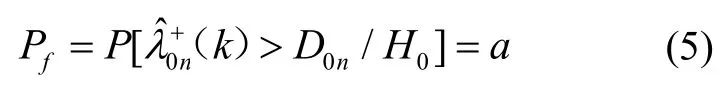
其中当限定误警率Pf=a时，则由式(5)解出的门限D0n可使漏检率„D0n/H0达到最小，因而门限D0n可由误警率Pf确定。

3 因子图融合与自适应隔离方法

当前组合导航中，信息融合一般采用集中式滤波或联邦滤波。当部分传感器出现故障时，必须重新构造系统和滤波器架构，这将影响导航系统的准确性和及时性。因此，导航系统的弹性滤波结构具有良好的研究前景，将有助于在干扰环境下实现导航系统的故障和隔离。

根据无人系统的实际特点，构建基于因子图的组合导航框架，如图3所示。系统中的信息源是INS和GNSS。将导航系统的状态和量测方程转化为两类因子节点。在图3中，紫色圆点表示变量节点，实心圆表示因子节点。xk表示系统的导航状态，p表示先验因子节点量测信息；u表示来自INS的测量信息，该信息与前后两个时间点的导航状态有关。m表示来自GNSS的测量信息。如果某个子导航系统因干扰而发生故障，则可以实时从系统中去除相应的因子。当某颗卫星伪距故障时，将该伪距量测隔离后，基于其他伪距量测形成GNSS因子节点。当惯性系统故障时，在因子图框架中隔离INS因子节点后，GNSS量测信息转化为主线上因子节点，导航系统实现依靠卫星量测的低频实时稳定工作。故障排除后，可以将该导航系统因子重新添加到因子图导航滤波器中。

图3 基于因子图的组合导航示意图Fig.3 Schematicdiagram of integrated navigation framework based on factor graph

在图3设计的方案中，使用东北天坐标作为导航坐标系。有三种状态变量，包括位置、速度和姿态。因子图的变量节点是维度系统状态，如式(6)所示。

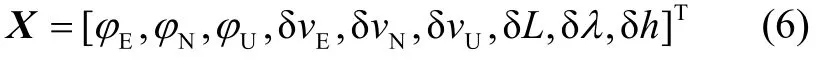
式(6)中，9个变量是惯性导航系统的导航输出参数。其中jE、jN、jU包括平台失准角；δvE、δvN、δvU是速度误差；δL、δl、δh是纬度、经度和高度误差。

因子节点的量测模型与各传感器相关，这里不再一一列举。根据每个子系统的状态和测量方程，使用标准的Levenberg-Marquardt 优化器计算因子图融合信息。基于因子图论和综合导航数学模型，融合方法如下所示。

每个因子代表一个最小化的误差函数。对于高斯噪声分布，表示测量模型的因子定义为：

式中hi(.)是预测传感器测量的非线性测量函数，zi是实际测量。

通过分析因子图导航系统的原理，系统状态估计函数是概率分布函数（PDF）的最大后验概率。在此基础上，我们基于故障检测校验结果添加权重因子，函数如下所示：

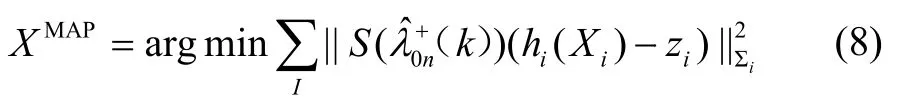
其中，hi(Xi)是观测函数，zi是实际测量值，Si是协方差矩阵。为权重函数，根据故障检测结果，隔离部分严重故障因子，调整融合权重，以削弱故障对导航系统的影响。

式(9)中，l1和l2为判断自适应隔离的上下门限，根据上一节的理论分析，由误警率Pf决定。选定误警率Pf=10-9，计算故障完全隔离检验门限l2=44.84；选定误警率Pf=10-3，计算故障自适应融合门限l1=16.27。

采用一阶泰勒展开对非线性观测方程hi(Xi)进行线性化，通过将观测方程引入最大后验概率估计，得到

式中Hi是雅可比矩阵，表示点Xi0处hi()的偏微分，Di是状态更新向量，为使得式(10)右侧取最小值的解。

当传感器出现故障时，传统的联邦滤波算法需要重构主滤波器，以防止故障传感器影响主滤波器。而因子图法只需要不连接故障传感器的因子节点即可实现故障隔离。

4 实验与分析

为了验证所提FDI 算法的有效性，基于复杂故障环境下仿真实验和实际跑车数据实验验证所提方法在存在惯性量测或者卫星导航系统伪距量测异常的情况下，能正常检测出伪距故障并提升导航定位性能。

4.1 仿真试验

根据自主车辆的实际路径要求，设计了一条800 秒的轨迹。如图4所示，起始点为118.79ºE、31.94ºN、5 m。三个方向的初始速度为0 m/s，起始点三个方向的初始姿态角为0 °。

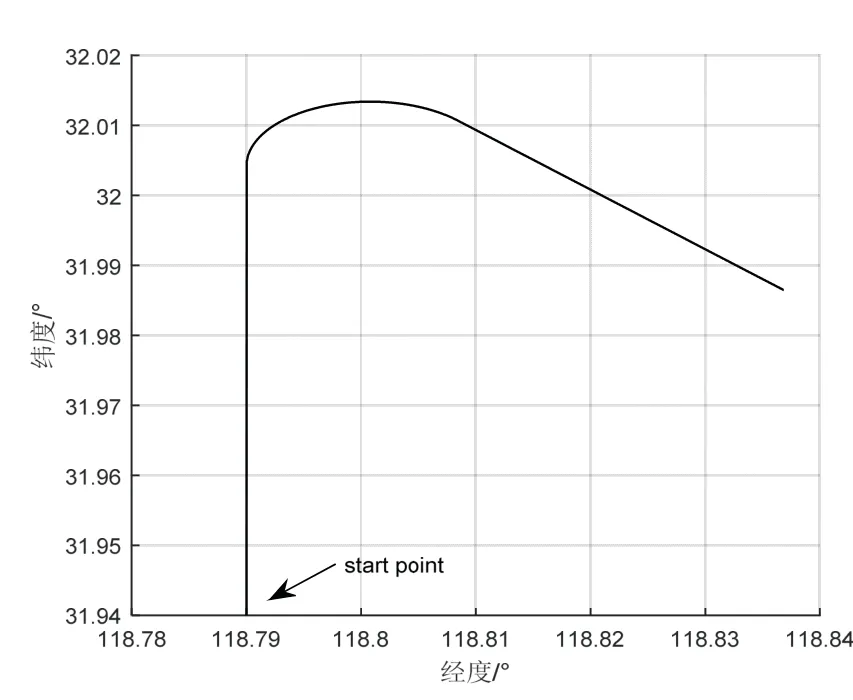
图4 车辆航迹图Fig.4 The path of vehicles

惯性导航系统的误差参数见表1，卫星导航系统的误差参数见表2，导航系统的故障模拟设置见表3。

表1 惯性导航误差Tab.1 Inertial navigation error

表2 卫星导航系统误差Tab.2 GNSS errors

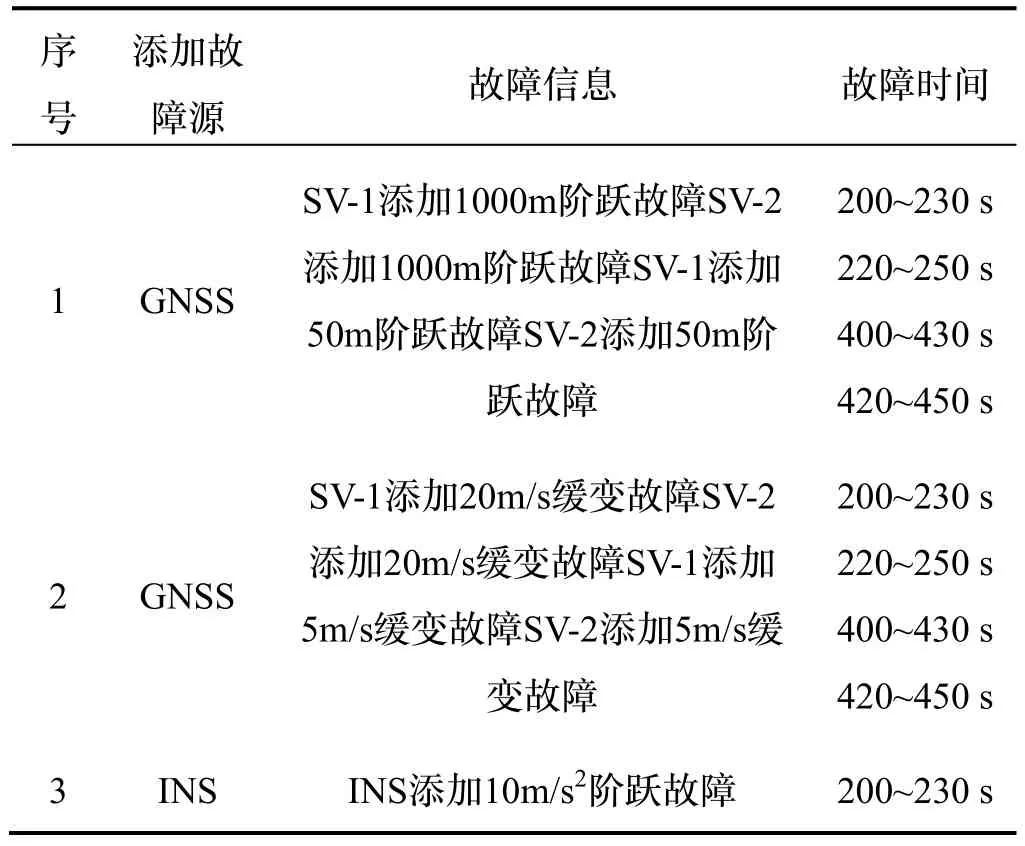
表3 各实验方案添加故障Tab.3 Add faults to each experimental scheme

阶跃故障和缓变故障是全球导航卫星系统伪距量测的典型故障类型。如表3所示，本文将各种故障（阶跃故障、缓变故障、单卫星故障、多卫星故障、大故障、小故障）添加到GNSS 伪距中。本文的实验验证在伪距量测中分别添加了振幅1000 m 的大阶跃故障、振幅50 m 的小阶跃故障和斜率为20 m/s 的大缓变故障、斜率为5 m/s 的小缓变故障，同时不同卫星伪距故障也有重合阶段，以测试所提算法的有效性。

仿真试验1：图5-6和表4比较了卡方检验法、伪距检测法和所提方法在GNSS 阶跃故障情况下的性能。

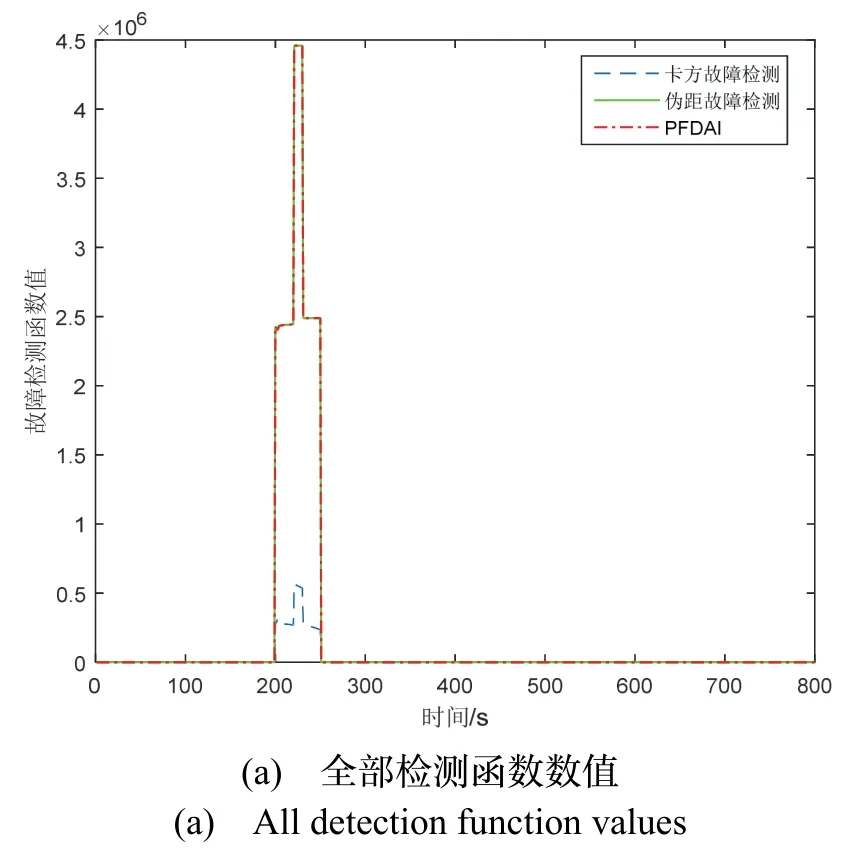
图5 多卫星阶跃故障下故障检测函数图Fig.5 The test statistic of fault detect obtained by simulation under the multi-satellites step fault

在图5中，SV-1 和SV-2 中由阶跃故障引起的主滤波器故障检测函数值图看出，由于所提方法和伪距检测法的故障检测原理相同，检验效果基本相同，曲线也基本重合，这三种方法都可以成功地检测多颗卫星中的大阶跃故障，而对小阶跃故障，传统依靠位置的方法难以检验，而对伪距检测法和所提方法，都可以正常的检测出故障，同时两颗卫星同时出现故障阶段校验函数也显著增加。

在图6中，对于大阶跃故障(200～250 s)，无论是单卫星故障还是多卫星故障，各个方法都可以成功检测到，依靠位置的卡方检测隔离掉卫星位置量测后会出现发散的情况，所提方法和伪距检测在隔离故障卫星伪距后，正常卫星数据可以像往常一样用所提方法校正惯性数据；而对于小阶跃故障(400～450 s)，所提方法可以自适应调节因子的权重，因此相较于伪距检测法，所提算法有着更好的精度。表4的误差RMS值同样证明了该方法具有更好的精度，针对故障阶段，所提PFDAI 方法相较于卡方检测法和伪距检测法三维位置精度分别提升了45%和35%。

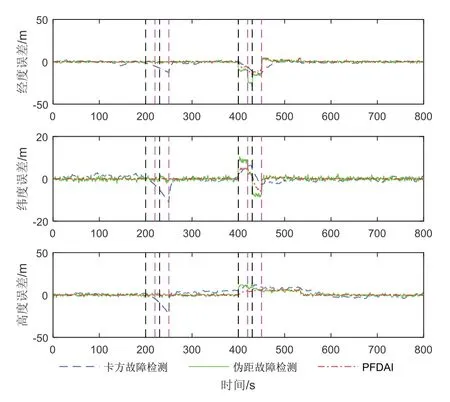
图6 多卫星阶跃故障下融合位置误差Fig.6 The fusion position errors obtained by simulation under the multi-satellites step fault

表4 多卫星阶跃故障下融合状态误差RMS 值Tab.4 RMS of navigation errors obtained by simulation under the multi-satellites step fault

仿真试验2：图7-8 和表5比较了卡方检验法、伪距检测法和所提方法在GNSS 缓变故障情况下的性能。在图7中，SV-1 和SV-2 中斜坡故障导致的检测统计图显示，不论是大缓变故障还是小缓变故障，所提出的方法和伪距检测法都可以更快地检测缓变故障。在图8中，在大缓变故障时，卡方检测隔离卫星位置后会出现短时的发散，而所提方法和伪距检测法都可以隔离掉故障伪距，效果近似；而在小缓变故障下，所提方法较伪距检测法有着更好的自适应效果，在多星伪距缓变故障中具有良好的检测和自适应隔离效果。RMS 表同样显示了本文方法的优越性，针对故障阶段，所提PFDAI 方法相较于卡方检测法和伪距检测法三维位置精度分别提升了29%和32%，如表5所示。

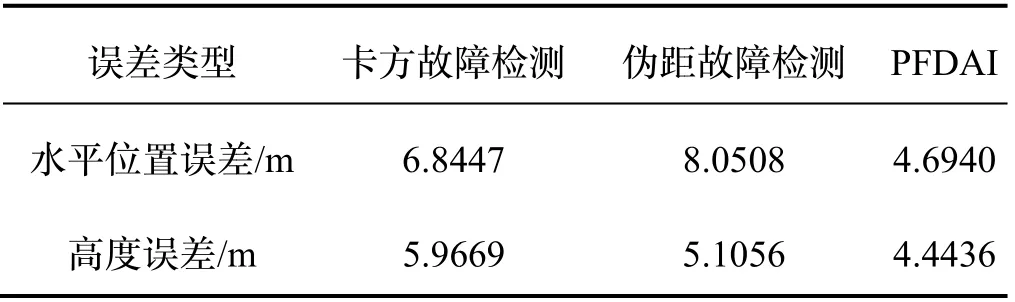
表5 多卫星缓变故障下融合状态误差RMS值Tab.5 RMSof navigationerrorsobtainedby simulation under themulti-satellites rampfault

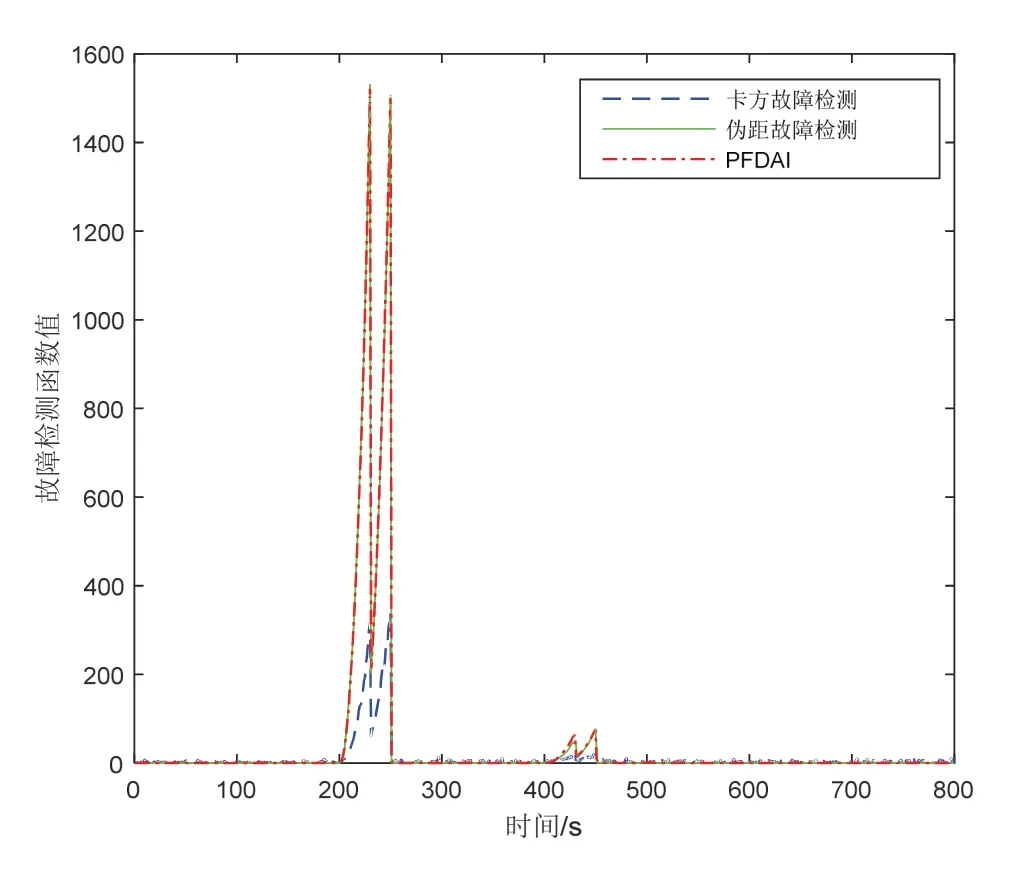
图7 多卫星缓变故障下故障检测函数图Fig.7 The test statistic of fault detect obtained by simulation under the multi-satellites ramp fault

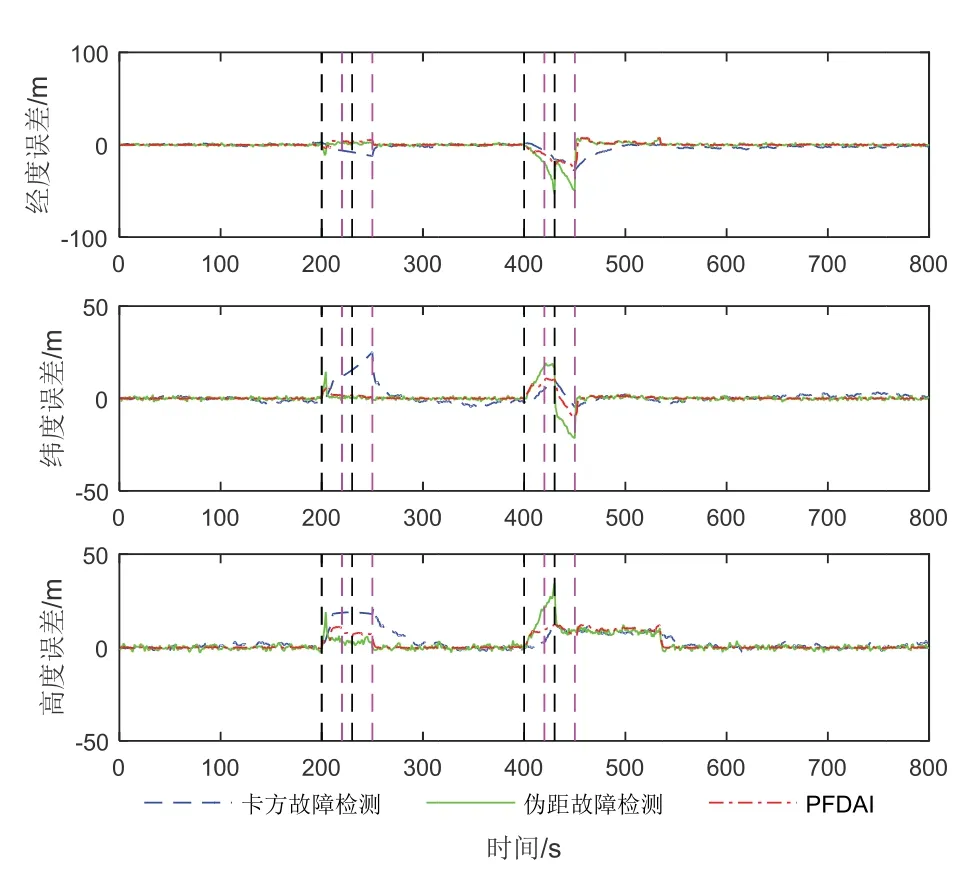
图8 多卫星缓变故障下融合位置误差Fig.8 The fusion position errors obtained by simulation under the multi-satellitesrampfault

仿真试验3：图9-10比较了卡方检验法和所提方法在INS阶跃故障情况下的性能，由于INS本身存在累积误差，小故障与缓变故障情况难以检测，但能通过融合进行修正，因此，本文仅考虑较大的INS阶跃故障，该情况下所提方法无需考虑自适应因子并且性能与伪距检测方法近似，所以不再单独对比。

图9 惯导阶跃故障下故障检测函数图Fig.9 Thetest statisticof fault detect obtained by simulation under INSstepfault

在图9中，传统的卡方检测方法将INS量测作为参考值，不能定位并隔离故障惯性传感器，因此其一直判断系统故障，无法恢复；而本文所提方法可以通过主子滤波器对比判断INS故障，隔离后可以正常检测系统故障和恢复。在图10中，由于传统卡方检测方法无法定位并隔离惯性系统故障，因此系统误差累积增大，最终发散；而本文方法可以正常隔离INS 故障，达到误差收敛的效果。

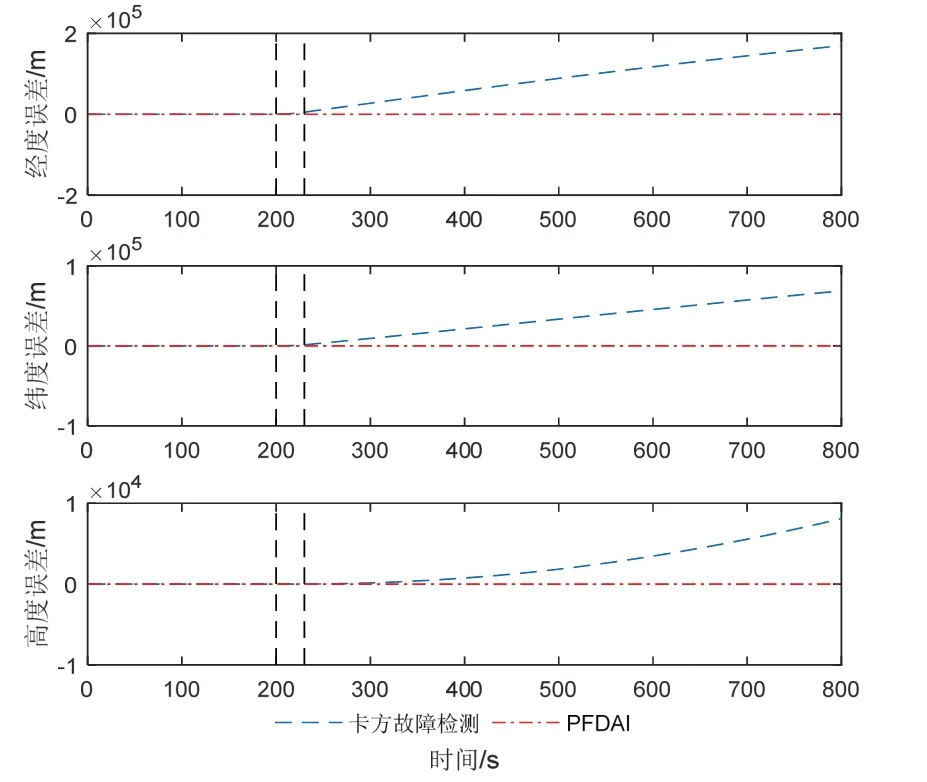
图10 惯导阶跃故障下融合位置误差Fig.10 Thefusion position errorsobtained by simulation under theINSstepfault

4.2 实际采集数据集实验

本文利用开放数据进行实验测试，采用香港理工大学提供的城市采集参考数据。该数据集通过香港理工大学车辆平台采集，车辆平台包括一个带有INS/GNSS的导航系统，以及来自SPAN-CPT系统的精确地面参考数据。车辆路径如图11所示，该环境为半城市峡谷环境，有部分地方有高楼遮挡造成伪距检测故障，部分低矮房屋也会造成伪距误差小范围波动，适合检测所提算法的效果。

图11 城市环境下车载实验平台轨迹Fig.11 The path of vehicleplatform under theurban environment

捷联惯性导航系统提供陀螺仪和加速度计数据，以计算地面位置、速度和方向信息。原始GNSS RINEX数据包括伪距、多普勒频移、星历数据。INS 测量由Xsens Mti-10 提供，频率为100 Hz 和200 Hz，原始GNSS 测量由u-blox M8T 收集，频率为1 Hz。由于香港的高层建筑，GNSS 信号容易受到反射或遮挡，导致非视线（NLOS）重新定位、多径效应或故障。与电磁干扰环境类似，传感器性能不稳定，容易发生故障。

图12和13均采用数据集UrbanNav HK 2020 分析了所提方法的性能。图10显示了城市峡谷环境中受影响的GNSS 信号引起的检测统计图。在图12中132 s～150 s 左右，由于高楼的遮挡，系统判断伪距出现故障，对伪距误差较大的卫星隔离后，进行自适应融合，而在270 s～299 s 左右，低矮楼房也造成了卫星定位精度略差，此时可以相应降低自适应权重，可以提升整体的定位精度。

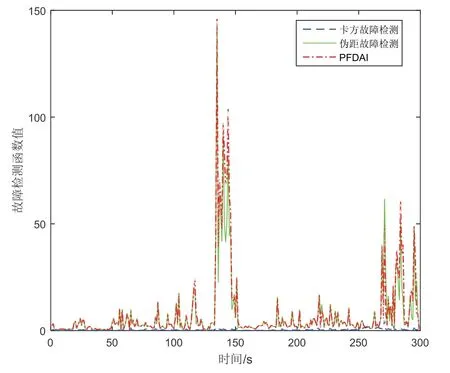
图12 香港城市环境下故障检测值Fig.12 The test statistic of fault detect obtained by the dataset UrbanNav-HK 2020

从图13可以看出，不论是在大伪距故障(132 s～150 s)情况下，还是小伪距故障(270 s～299 s)情况下，所提算法的红色曲线相较于传统依赖位置进行卡方检测法还是依赖伪距进行检测隔离的方法都可以自适应地调整，适当地降低GNSS 因子的权重，提高短时间内的定位精度。

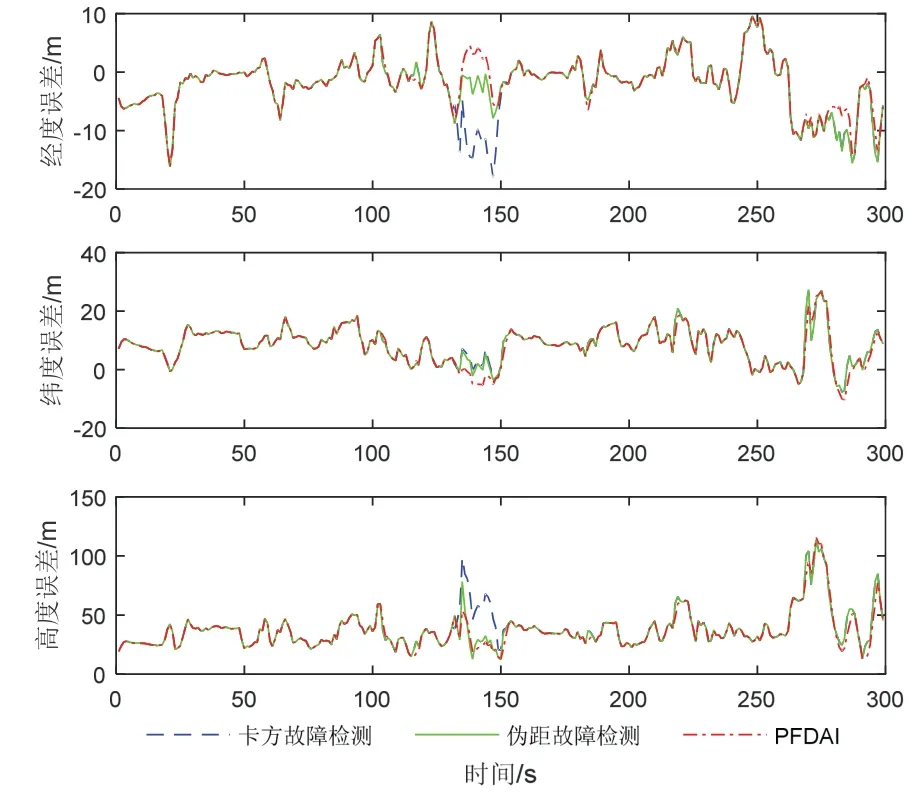
图13 香港城市环境下融合位置误差Fig.13 The fusion position errors obtained by the dataset Ur-banNav-HK 2020

从表6可以看出，提出PFDAI 方法在故障期间的水平位置精度和高度精度相较于传统卡方检测法提高了14.35%和12.05%。

表6 香港城市环境下融合状态误差RMS 值Tab.6 RMS of navigation errors obtained by the dataset Ur-banNav-HK 2019 under the satellite fault

5 结 论

对于因子图的即插即用框架，有效的故障检测和隔离方法以及在未知干扰下的鲁棒导航对安全至关重要。为了提高复杂环境下组合导航系统的故障检测和鲁棒性能，提出了一种基于因子图导航的伪距故障检测与自适应隔离方法。它提供了卫星伪距故障定位的能力，并在检测结果的基础上进行自适应隔离，提升故障下系统定位精度。本研究得出的结论可总结如下：

（1）基于因子图的组合导航算法能够有效地解决导航信息融合中的传感器异步问题，实现多传感器的灵活配置，因此得到了广泛的应用。

（2）基于INS 和GNSS 伪距测量，设计了一种基于因子图组合导航的伪距故障检测方法，并在检测结果的基础上自适应隔离故障量测，提升故障下的导航定位效果。

（3）仿真和基于实测数据的试验结果表明，在GNSS 伪距阶跃故障、缓变故障、单卫星故障、多卫星故障、大小故障下的故障检测与隔离性能得以改进。仿真试验显示不同故障下所提方法相较于卡方检测法和伪距检测法三维位置精度均提升29%以上，基于跑车公开数据集数据的试验结果表明，与传统卡方的故障检验与隔离方法相比，本文提出的故障检测和自适应隔离方法的导航水平位置精度和高度精度均提高12%以上。