基于模型预测静态二阶锥规划的协同末制导

权申明，左 坤，晁 涛，杨 明

（哈尔滨工业大学 控制与仿真中心，哈尔滨 150080）

单个飞行器在对目标探测与机动能力上均存在一定的局限性，传统单飞行器对目标制导效果有限。相比之下，多飞行器协同探测目标存在更大的优势，多飞行器可同时进行探测识别与信息交流，显著提高对真实目标的识别能力。多飞行器协同还能降低飞行器的弹载计算和探测设备的要求，从而降低成本。

在协同末制导阶段，相关学者针对不同约束条件进行制导律设计。赵久奋等人[1]针对推力可控的导弹，在视线和视线法线方向上，结合超螺旋算法和有限时间滑模设计分布式协同制导律，并针对机动目标进行仿真验证。肖惟等人[2]研究了考虑过载约束的多枚弱机动能力导弹强目标协同问题，结合飞行器可达域、可行域以及目标逃逸域，设计了协同拦截策略。司玉洁等人[3]研究了考虑通讯拓扑条件下的协同末制导律，并基于有限时间理论设计快收敛的滑模制导律。此外，强化学习等方法也用于协同末制导律设计中，并取得较好的制导效果。

模型预测静态规划（Model Predictive Static Programming,MPSP）自Padhi 等人[4]提出以来，在飞行器制导控制[5-10]方面有较多的应用，该方法在计算效率和制导精度上具有一定优势。MPSP 根据灵敏度矩阵不断更新控制量，能够满足终端约束[11]，后续研究中，输入与状态约束逐渐引起关注[12,13]。文献[14]考虑中制导过程中，零控拦截和交班视窗角约束，推导了时间固定的广义模型预测静态规划算法。文献[15]基于优化模型预测静态规划算法，针对吸气式高超声速飞行器设计了满足终端碰撞角约束的制导律。文献[16]提出了一种初、中制导联合规划制导方法，用于解决多阶段目标拦截问题。在MPSP 的基础上，广义MPSP 算法被提出[17,18]，该方法无需对动力学模型离散化，提高算法求解速度与精度。

MPSP 算法同模型预测控制有相似之处，离散步长通常为定值，因此难以处理终端时间自由的问题。然而，在协同末制导问题中，终端时间难以事先获得；同时，初始轨迹的选取影响了优化结果与优化效率。

针对现有序列二阶锥规划（Second-Order Cone Programming,SOCP）求解协同制导问题速度较慢难以满足实时性要求的问题，本文结合MPSP 与SOCP，提出一种基于模型预测静态二阶锥规划的协同末制导算法。首先，建立考虑过载约束的飞行器协同末制导模型；然后，在MPSP 算法基础上，提出终端时间自由的MPSP 算法；进一步将有状态约束的MPSP 问题转化为模型预测静态二阶锥规划问题，可以有效处理过程约束。仿真结果表明，所提出的模型预测静态二阶锥规划能兼备MPSP 算法的快速性与SOCP 的处理约束与最优性特点，通过减少求解变量个数，提升求解速度，易于实现在线快速计算。通过不同仿真场景、不同优化方法的仿真与分析，验证了本文所提算法的计算效率与精度。

1 问题描述

建立发射系下飞行器运动模型为：

其中，i为每个飞行器的编号，xi、yi、zi、Vi分别表示第i个飞行器的在空间坐标系下的位置分量、速度大小，θi、σi、γi分别是第i个飞行器的弹道倾角、弹道偏角、倾侧角。Di、Li分别是第i个飞行器在飞行过程中受到的阻力与升力，速度系下气动力分量为：

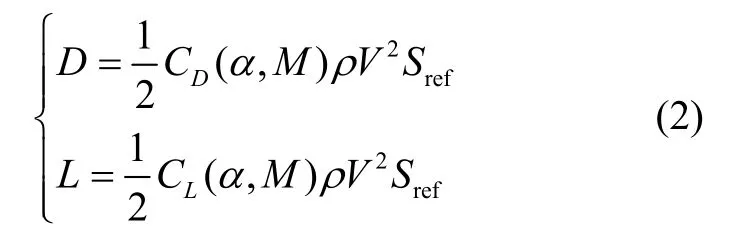
其中ρ=ρ0e-y/hs是大气密度，ρ0为标准大气密度，hs为标准高度。Sref为飞行器的最大横截面积。CL和CD分别是升力与阻力系数，由飞行攻角α与飞行马赫数M计算得到，马赫数的数值大小由飞行器的飞行速度进行计算。

在飞行器协同飞行过程中，需满足初始状态约束、终端状态约束以及过载约束。其中，过载约束为：

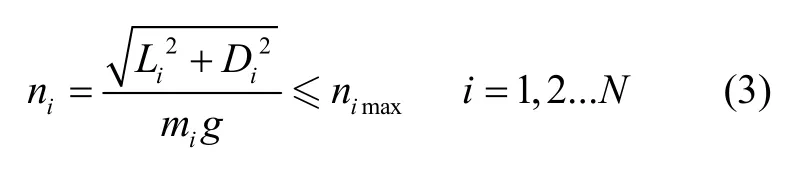
2 算法设计

本节首先进行终端时间固定、无过程约束MPSP算法介绍。在此基础上，提出考虑过载约束的终端时间自由协同打击末制导算法。

2.1 终端时间固定的MPSP 算法

记离散时间的非线性动力学系统为：

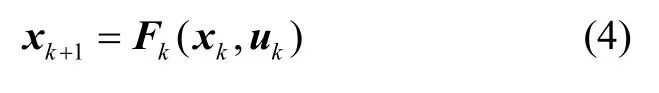
其中，k=1,2,......N-1为一系列的离散点，离散步长为tN为设定的终端时间，x∈Rn是系统的状态变量，u∈Rm是系统的控制变量，F关于x与u连续可导，与飞行器的动力学方程有关，MPSP的目的是找到合适的du，对于先前的输入up进行校正（上角标p表示上一次迭代结果），得到新的控制量u=up+du，状态变量随之得到更新。即：x=xp+dx。其中du、dx分别是控制变量与状态变量的增量。

假设状态变量的变化dx与控制变量的变化du较小，那么在更新k+1时刻的状态时，可以对离散的状态方程进行泰勒展开，考虑一阶展开形式：

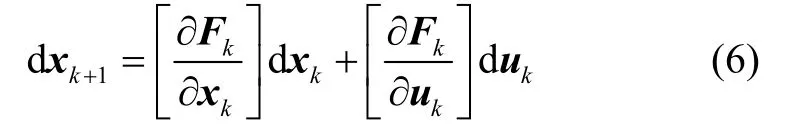
同理可以得到：

将式(7)代入式(6)，得：

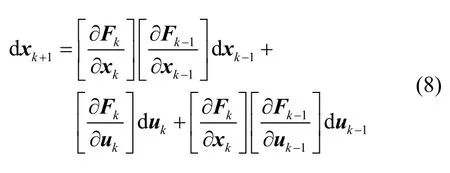
不断迭代可得：

其中，

其中j=1,2…k-1。

当j=k时，有：

初始状态通常为给定值，那么dx1=0，则式(9)可写为：

式(13)表明，第k+1个时间点的状态是由前k个控制量进行校正的，为简化B阵的计算，引入中间变量：

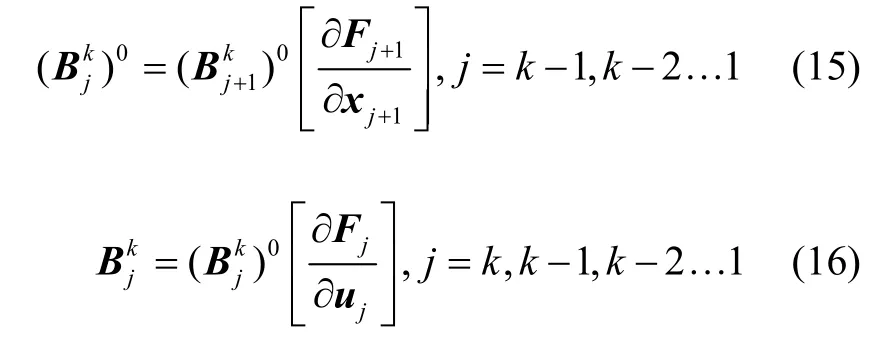
至此B计算完成，称B为灵敏度矩阵。

2.2 基于二阶锥规划终端时间自由的MPSP

考虑终端时间自由的离散时间的动力学系统方程：

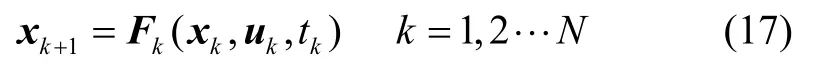
其中，k表示第k个离散点，系统的非线性动力学方程为f(xk,uk)，本文离散点总数N保持不变，终端时刻变化后，每一个离散点表示的时间将不断改变，离散时间间隔tk为：

将模型(17)在前一次结果(xkp,ukp,tkp)的基础上进行线性化，可以得到：

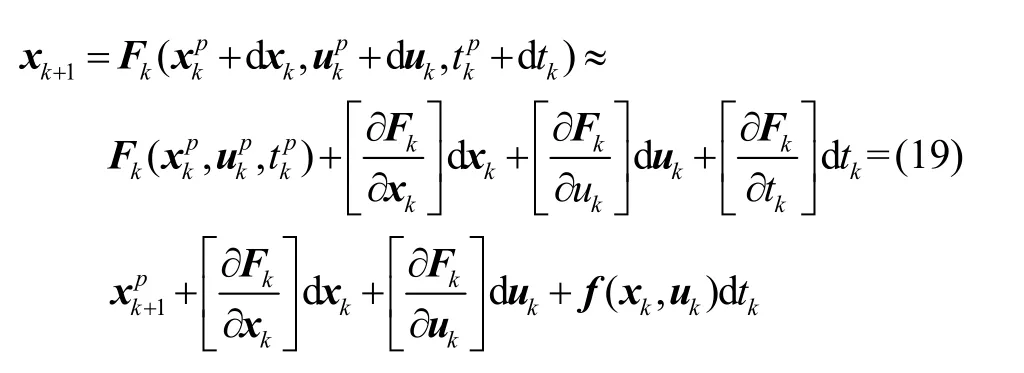
其中，终端时间的变化量为dtN=tN-tNp，每个离散时间间隔的变化量为表示前一次迭代得到的终端时间。

满足上述式子的du很多，难以获得解析解，因此使用优化的思想来进行求解。

构造目标函数为：

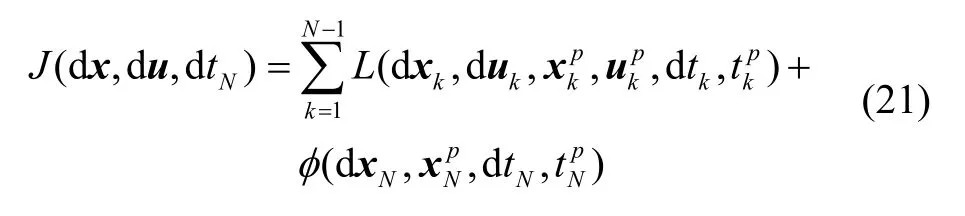
其中，L为过程中的优化目标，φ为终端时刻的优化目标。本文不仅考虑终端约束的影响，还要考虑过程约束。过程约束与控制约束线性化后可以写成如下形式：

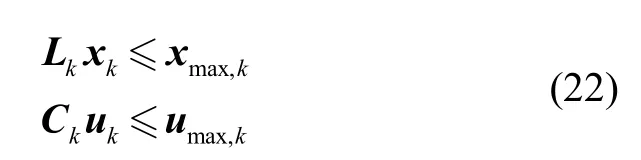
其中，Lk、Ck与具体的约束有关，已知代入式(22)可以得到：

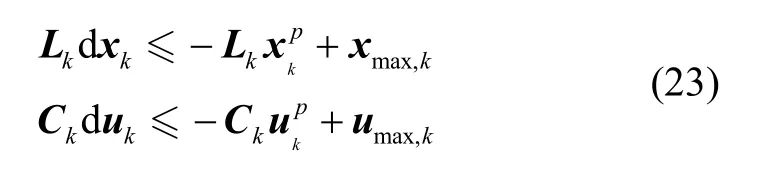
由上述不等式可知，上述约束为一个凸约束，可以使用二阶锥规划方法解决。

综上，初始状态为x1*，期望终端状态为xf*，可以将求控制变量du与终端时间tN的问题转化为一个模型预测静态二阶锥规划（MPSP&SOCP）问题：

由于在MPSP&SOCP 中，优化变量只有终端时间和输入量的偏差，因此无法直接计算迭代过程中的过载大小，采用一阶泰勒展开近似线性化后，通过逐级求导可得到攻角对速度、高度的影响，进而通过序列迭代求出过载值，具体如式(25)：

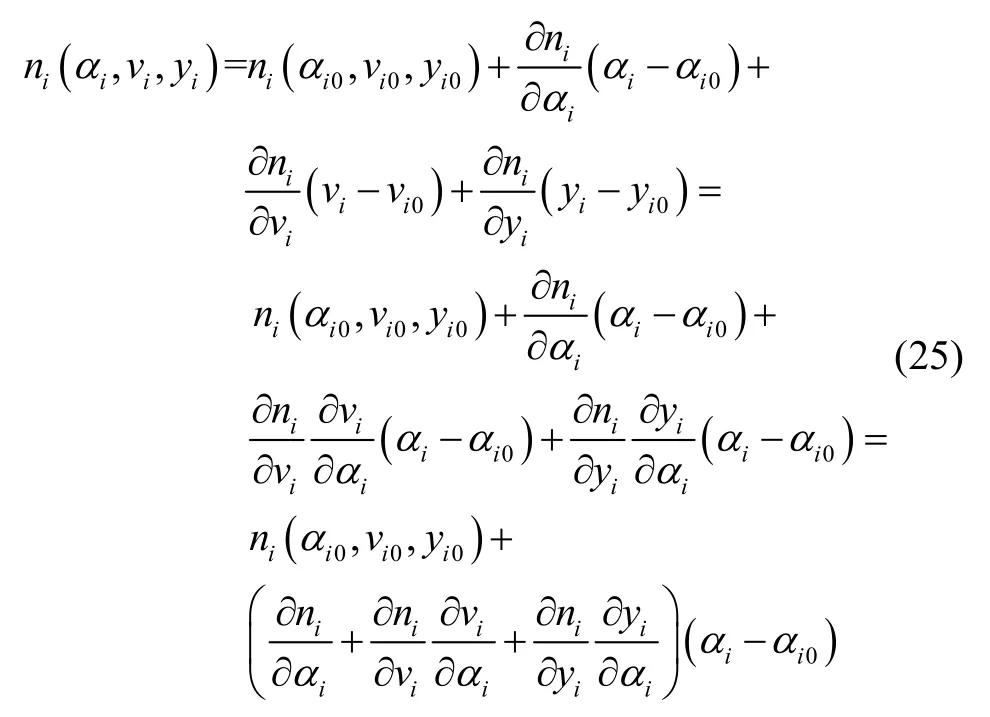
设计MPSP&SOCP 算法求解流程如图1所示。

图1 MPSP&SOCP 算法流程图Fig.1 MPSP&SOCP algorithm flow chart

MPSP&SOCP 算法需要设置初始轨迹，传统MPSP 求解末制导问题时，往往通过比例导引进行初始轨迹的计算。本文中，为了降低算法对初值的依赖性，提高算法的适应性，采用常值控制量，开环积分后得到初值。在求解带有过程约束最优问题时，第一次迭代时，仅加入终端位置约束，在求得结果基础上，增加终端角度约束。通过将约束条件逐步加入，可以有效提升求解速度与算法稳定性。计算灵敏度矩阵后，将过程约束转化为SOCP 问题，仅需求解控制量的更新值即可，无需进行状态量的优化，大大减少了求解时间。

3 数值仿真及分析

为了验证本文所提算法的有效性与适应性，本节分别进行无过程约束MPSP 末制导仿真、考虑侧窗约束MPSP 末制导仿真、对比算法仿真以及适应性仿真实验。其中，选取文献[19]中SOCP 算法作为对比算法。

飞行器的升力系数与阻力系数是关于攻角和马赫数的多项式，如式(26)所示：

协同飞行器数量为3（M1、M2、M3），飞行器质量为907.8 kg，面积为0.355 m2，最大过载约束为1.5g，仿真中初始条件如表1所示。

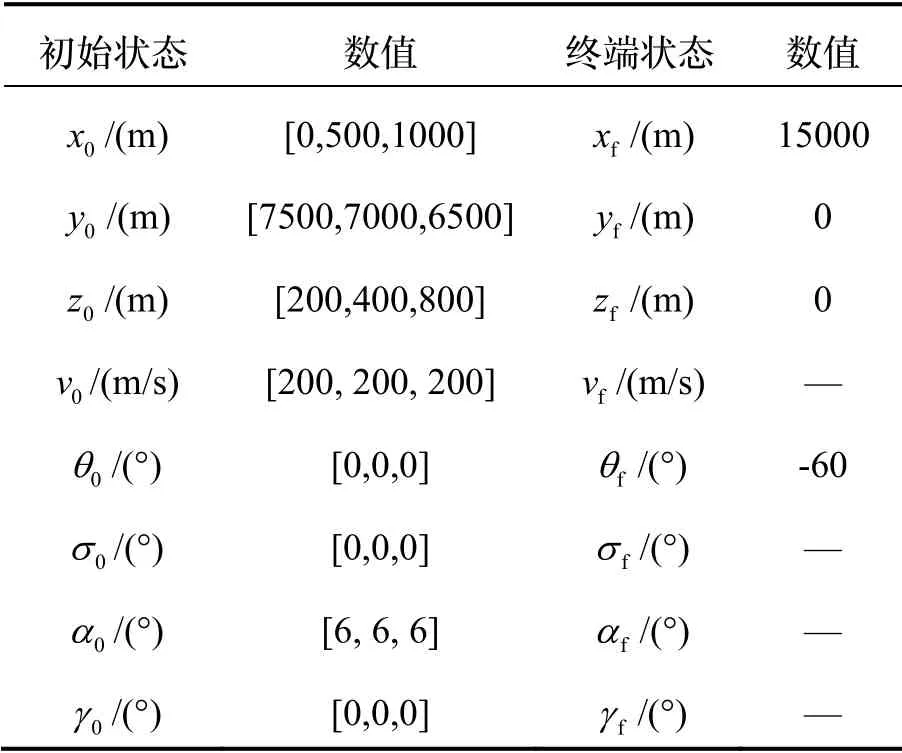
表1 仿真初始条件Tab.1 Initial conditions of simulation

3.1 二阶锥规划方法仿真结果

在相同仿真条件下，采用二阶锥规划方法进行对比仿真，仿真结果如图2-7所示（图中Initial 表示第一次求解得到的轨迹，Opt 表示最终优化轨迹）。

图4 速度倾角变化曲线Fig.4 Flight path angles

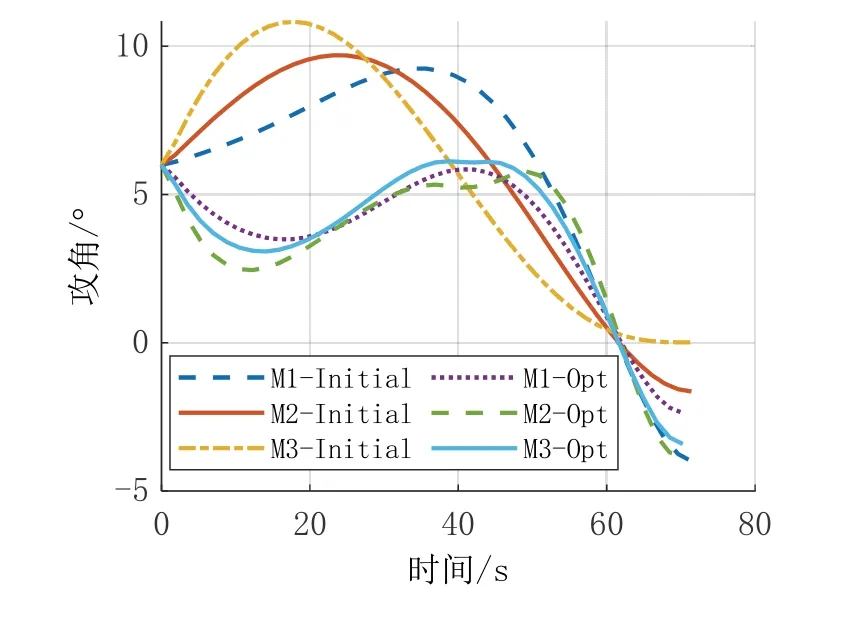
图5 攻角变化曲线Fig.5 Angles of attack

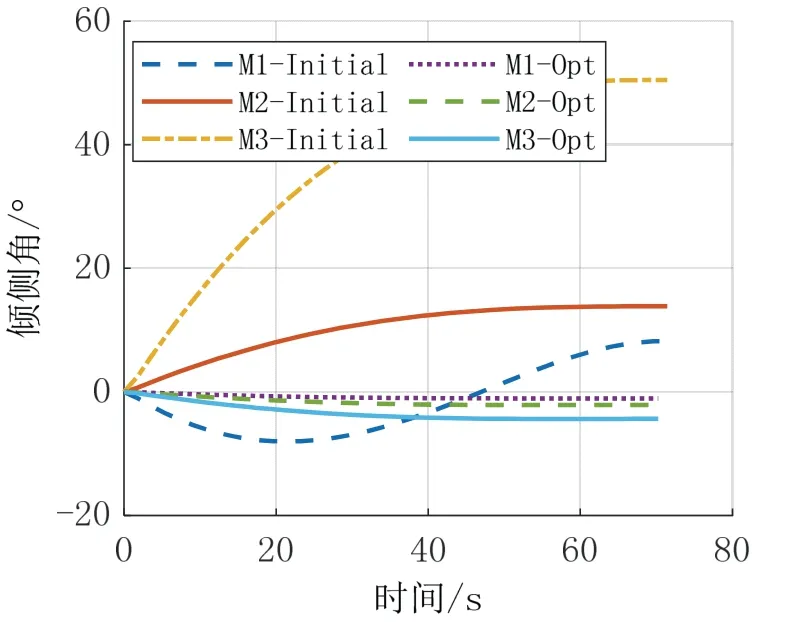
图 倾 化曲Fig.6 Curves of bank angles

由仿真结果可以看出，基于二阶锥规划方法的协同末制导可以实现对目标的精确打击。该算法首先加入终端位置约束，因此图7中第一次求解结果中峰值过载接近2.4g，然后考虑终端速度倾角约束，在上述结果基础上，考虑过载约束能够实现收敛，同时过程约束满足要求。

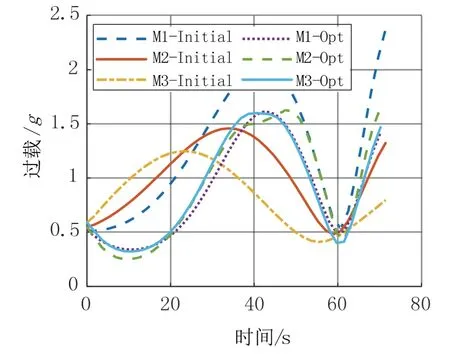
图7 过载变化曲线Fig.7 Curves of overload

3.2 MPSP&SOCP 算法仿真结果

基于MPSP&SOCP 算法仿真结果如图8-14所示（图中Guess 表示初始猜测轨迹，Opt 表示计算得到的最优轨迹）。

图8 三维轨迹Fig.8 Curves of 3D trajectories

图9 速度变化曲线Fig.9 Curves of speed

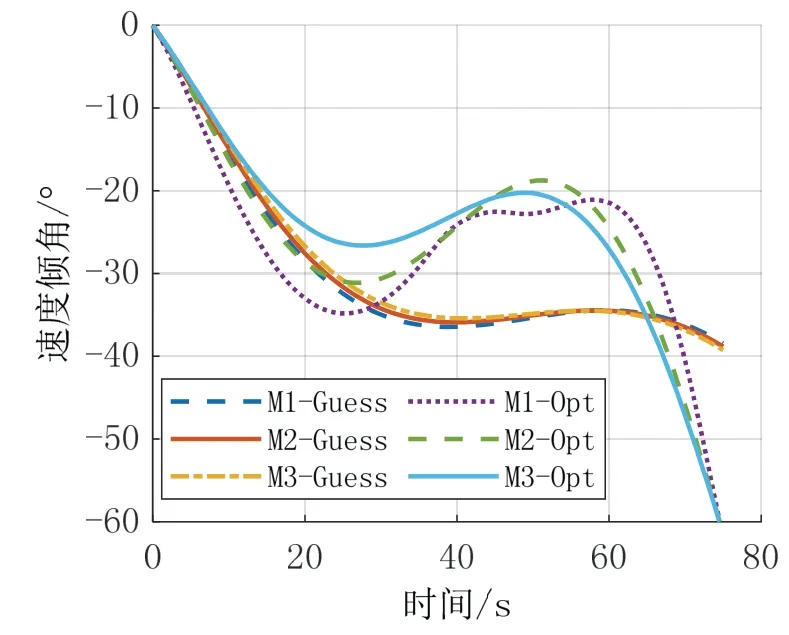
图10 速度倾角变化曲线Fig.10 Flight path angles

图11 攻角变化曲线Fig.11 Angles of attack

图12 倾侧角变化曲线Fig.12 Curves of bank angles

图13 过载变化曲线Fig.13 Curves of overload

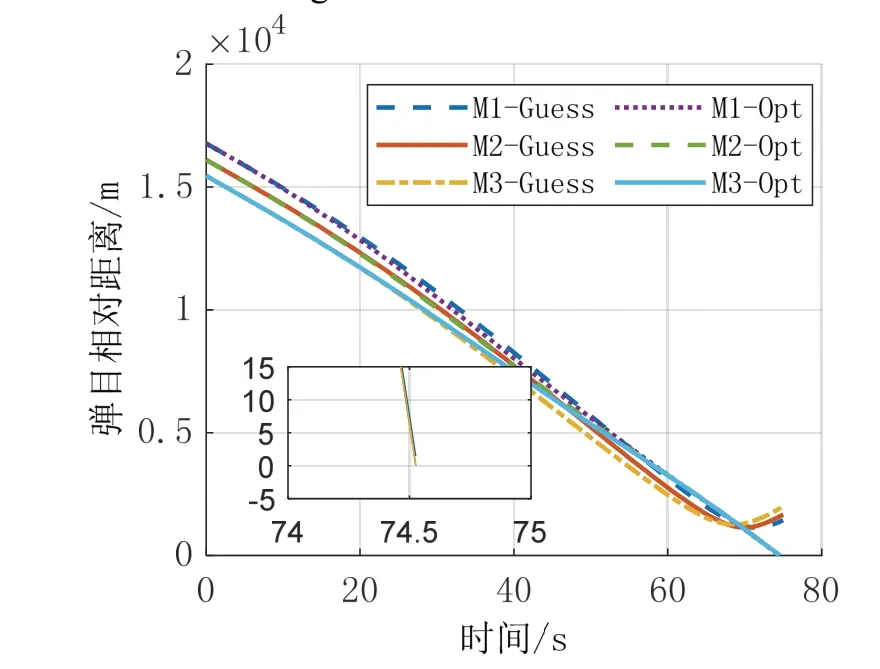
图14 相对距离变化曲线Fig.14 Curves of relative distances

由图8可以看出，3 个飞行器由猜测控制量开环积分得到的轨迹不满足终端位置约束，飞行器1 和飞行器3 相距目标点较远，3 个飞行器终端高度为负，图11和图12中开环控制量相同，因此各飞行器初始轨迹相似。在第一次迭代中，仅加入终端位置约束，从第二次迭代开始，加入终端弹道倾角约束如图10。由于末制导阶段飞行器高度下降较快，阻力减速效果没有重力势能转化为动能的效果明显，因此图9中速度略有增加。经过MPSP&SOCP 迭代计算后，能够实现对目标的精确打击。

本仿真算例中，过载约束为1.5g，初始轨迹中由于控制量变化率为常值，因此过载较小，最大过载为1.1g，在优化中考虑过载约束，求得图13中最优轨迹满足过载约束。

3.3 对比分析

将两种方法得到的最优轨迹进行对比，如图15所示。可以看出基于SOCP 与MPSP&SOCP 的求解三维轨迹相吻合。

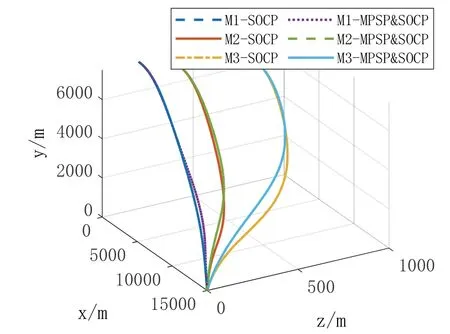
图15 不同方法求解结果Fig.15 Results of different methods

对终端位置约束进行小范围改变，变化范围为原点附近水平面内1000 m 的半径圆区域，进行50 次蒙特卡洛仿真。统计终端时刻脱靶量，如图16所示。可以看出两种方法求解精度均在2 m 以内。

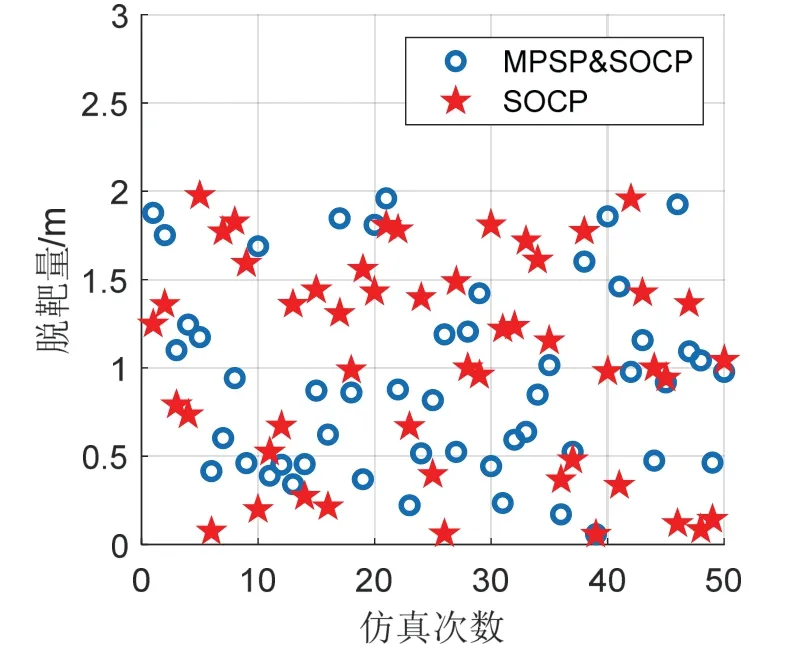
图16 求解精度对比Fig.16 Solving accuracy comparison

将上述MPSP&SOCP 算法与二阶锥规划的求解效率进行对比仿真分析，结果如图17所示，可以看出在同等迭代次数、求解精度情况下，MPSP&SOCP算法能够节省40%的时间，有望实现在线实时规划求解。

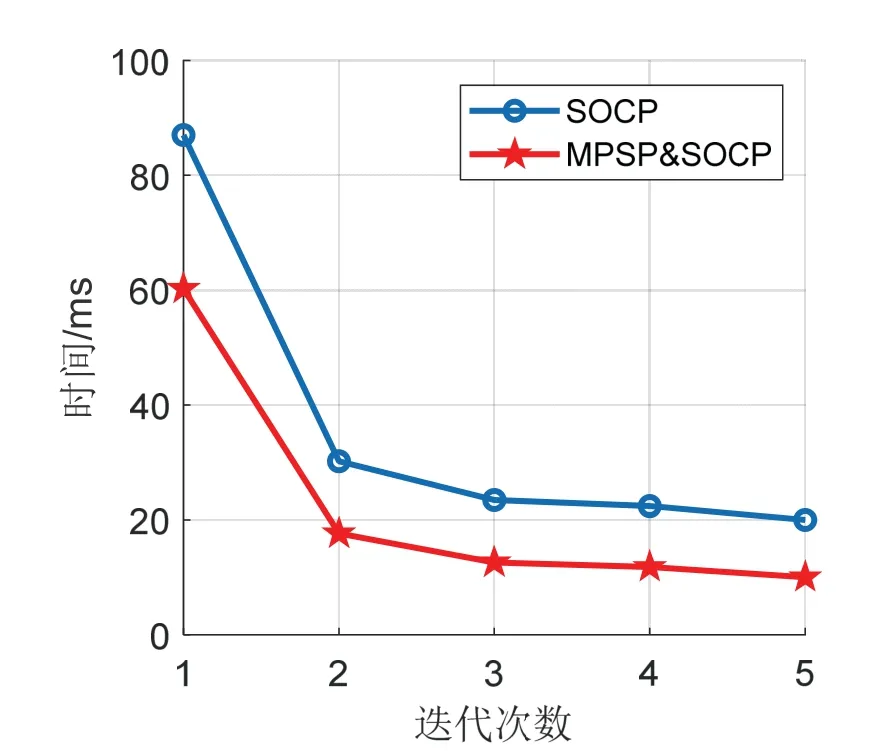
图17 求解效率对比Fig.17 Solving efficiency comparison

综上，基于MPSP&SOCP 算法的协同末制导可以在保障求解精度的前提下，耗费更短的时间，易于实现在线计算，工程前景广阔。

4 结 论

本文针对现有序列二阶锥规划求解协同打击问题速度较慢难以满足实时性要求的问题，结合MPSP 与SOCP，提出一种基于模型预测静态二阶锥规划的协同末制导算法。主要结论如下：

(1) 在MPSP 算法基础上，提出终端时间自由的MPSP 算法，能够解决传统MPSP 问题终端时间固定的缺陷，求解时间最优问题。

(2) 为了解决传统MPSP 算法过于依赖初始轨迹的局限性，提出逐步增加约束条件的迭代求解流程，从而使得小偏差线性化更具合理性，算法稳定性更强。

(3) 所提出的模型预测静态二阶锥规划能兼备MPSP算法的快速性与SOCP 的处理约束与最优性特点，通过减少求解变量个数，提升求解速度，易于实现在线快速计算。

本文目前工作从轨迹优化的角度进行，后续将开展在线实时优化-跟踪的闭环制导算法研究，同时考虑更多的约束条件，以增加本文算法的适用性。