捷联主动雷达末制导信息提取及延时补偿设计

2022-05-15严大卫钟婧佳

中国惯性技术学报 2022年1期

陈喆，吕瑞，杜肖，严大卫，钟婧佳

（中国运载火箭技术研究院，北京 100076）

捷联相控阵雷达相比平台式机扫雷达因去掉了机械框架，具有结构简单、体积小、质量轻、成本低等诸多优点，在高速飞行器中得到了广泛应用[1,2]。由于捷联主动雷达不能直接获取制导所需的视线角速度信息，且波束指向与载体姿态运动存在耦合，测角信息带有更强的噪声，因此采取简单有效的捷联解耦算法准确获取视线角速度信息成为了捷联末制导研究的重要问题之一[3-5]。

关于捷联解耦，国内外众多学者进行了大量研究，主要包括基于坐标转换的捷联信息解耦、前馈姿态调节波束稳定解耦、卡尔曼滤波估计解耦等几类方式[6]。文献[7-9]根据载体姿态及弹目视线关系在惯性系重构视线角，然后利用微分跟踪器或鲁棒控制等方式实现了视线角速度计算，这也是目前较常见的惯性系解耦思路。文献[10-12]则基于自适应或无迹卡尔曼滤波完成捷联解耦并提高估计准确度，但部分方法引入的遗忘因子如何选取直接影响最终精度。文献[13-14]为应对捷联外界强烈干扰，采用连续离散增广状态卡尔曼滤波、增广容积卡尔曼滤波来提取视线角速度信息，模型相对复杂。文献[15]则另辟蹊径采用分段制导、一体建模等方式解决了捷联耦合与视场约束问题。

以上研究多集中于无约束惯性系解耦，偶有带终端约束的也甚少考虑地球曲率影响，本文为兼顾不同目标距离下落角适应性，通过构建目标坐标系并结合扩展卡尔曼滤波及惯组延时补偿给出了一种目标系下解耦设计方法。

1 捷联主动雷达解耦建模

1.1 雷达探测角度

针对捷联主动雷达，以雷达载体中心轴为x轴构建载体坐标系，以雷达天线阵面法线为x轴构建天线坐标系（两系y轴均位于载体纵向对称面内），两坐标系之间可通过天线安装角转换。

主动雷达稳定跟踪目标后，主要输出目标指向在天线坐标系中的角位置用于目标定位。以目标指向为x轴构建雷达视线坐标系（y轴位于载体纵向对称面内），则目标位置可由天线坐标系中的雷达视线角（由雷达看向目标）描述，具体如图1所示。

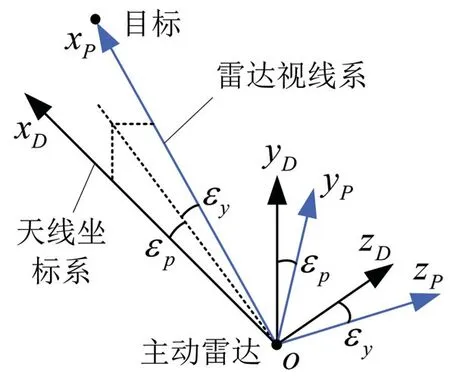
图1 雷达探测角度示意图Fig.1 Diagram of detection angles of radar

其中，天线坐标系到雷达视线系默认为3-2 转序，εp为雷达视线高低角，εy为雷达视线方位角，天线坐标系与雷达视线系可通过这两个角度进行转换。

1.2 基于目标系的视线角解耦

根据文献[7-9]，目前针对捷联雷达甚至捷联红外探测器，传统方式都是根据视线坐标关系在惯性系构造视线角qp、qy实现捷联解耦，具体如图2所示。

图2 惯性系视线角与目标系视线角Fig.2 LOS angles of inertial and target coordinates

当有落角约束时，由于地球曲率的影响，惯性系终端视线角qp会随着目标距离越远与目标点当地视线角λD差异越大，导致惯性系解耦需要根据目标距离或球心角在落角上进行补偿才能满足终端约束。此处考虑在预估目标点建立x轴指向正北（也可其他指向）的目标坐标系和x轴指向雷达的目标视线系（两系y轴均位于雷达-目标连线纵向平面内），根据各坐标系之间的相互转换关系在目标系下实现捷联解耦，具体如图3所示。

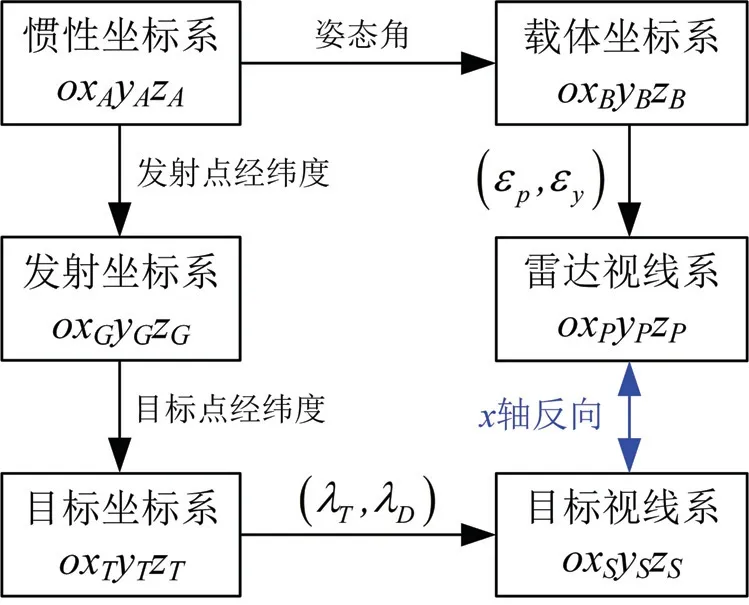
图3 坐标系间相互转换关系Fig.3 The transformation between coordinates

由于目标视线系和雷达视线系的x轴同轴反向，对于在目标点视线方向的单位矢量，它在目标视线系与雷达视线系的坐标分别为［1 0 0］T、［-1 0 0］T，根据图3的坐标关系统一转到目标系下可得：

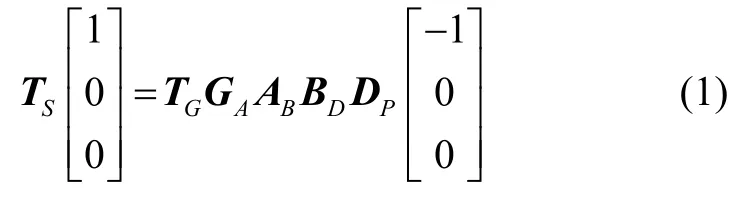
其中，A表征惯性系，G表征发射系，T表征目标系，S表征目标视线系，B表征载体系，D表征天线系，P表征雷达视线系，AB表征载体系到惯性系的转换矩阵，其余符号含义类同。

式(1)等号左边展开有：

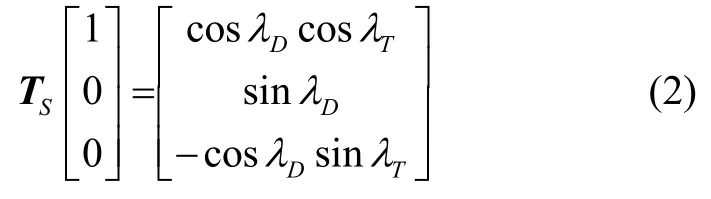
式(1)等号右边包含了DP矩阵，展开后是关于εp和εy的一个较长的解析表达式，简记作：

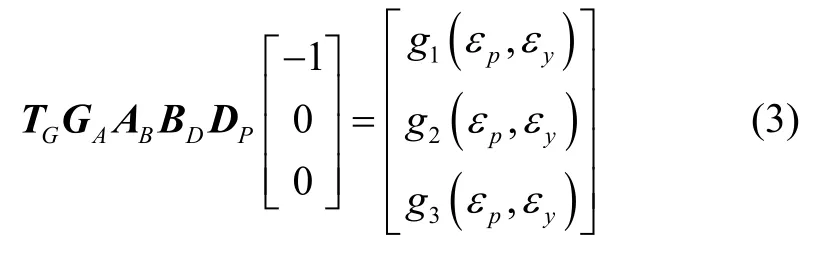
联立式(2)与式(3)，则目标系视线角（由目标看向雷达）为：

其中，λD为目标系视线高低角，λT为目标系视线方位角，该角度信息输出用于制导解算。

1.3 雷达视线角与目标系视线角关系

将式(1)转换到天线坐标系下有：

式(5)等号左边包含了TS矩阵，展开后是关于λD和λT的一个较长的解析表达式，简记作：

联立式(5)与式(6)，则雷达探测视线角（由雷达看向目标）为：

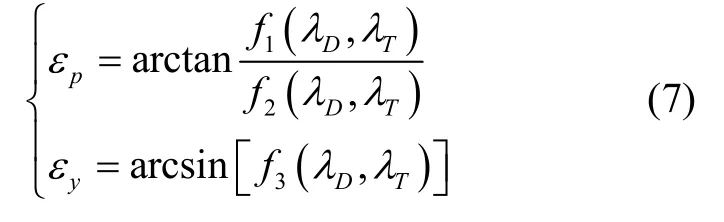
2 扩展卡尔曼滤波提取视线角及角速度

由于式(4)只得到了视线角并无视线角速度，若采用的制导方法需要用到角速度信息，最直接的方法就是差分，但差分容易放大噪声影响，导致效果不佳，可通过滤波的方式获取视线角速度等信息，降低误差干扰影响。

2.1 滤波模型

根据科氏定理及雷达与目标的相对运动关系建立运动学模型如下：

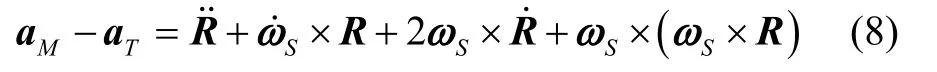
其中，ωS为目标视线系相对目标系的转动角速度，R为雷达与目标的相对距离，aM、aT分别为雷达与目标的运动加速度。

将式(8)在目标视线系中展开，转动角速度为：

对式(9)求导得到转动角加速度为：

联立式(8)-(10)整理后可得：

对式(11)各行展开，得滤波模型方程为：

2.2 滤波状态方程

根据式(12)的滤波模型，选取目标系视线角、视线角速度及相对距离与相对速度为状态变量。

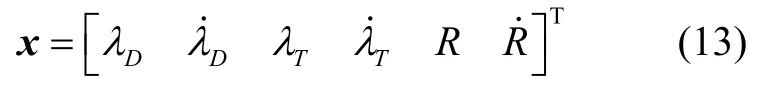
得到非线性状态方程并简写记作：

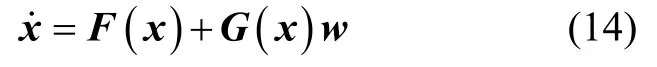
其中，

2.3 滤波观测方程

以雷达探测的视线高低角、方位角、测距值、测速值作为观测量，则系统观测方程为：

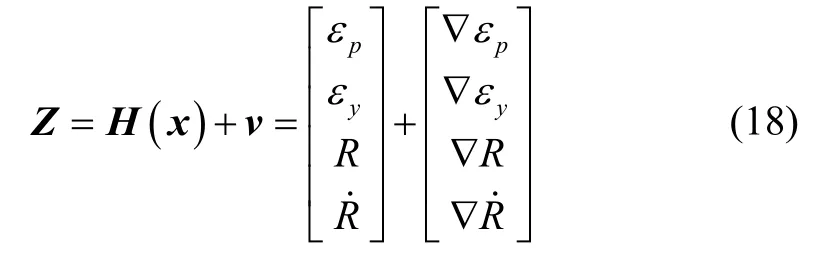
其中，v为各观测量噪声。

2.4 扩展卡尔曼滤波

模型式(14)为非线性系统，可以采用扩展卡尔曼滤波对状态量进行估计。首先将状态方程写成周期为ΔT的一阶离散形式。

其中，

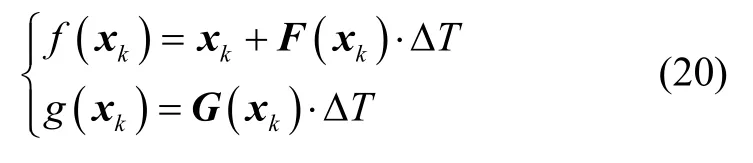
针对上述离散非线性系统，利用扩展卡尔曼滤波算法提取视线角及角速度的步骤如下：

步骤1：对滤波状态进行一步预测；

步骤2：计算状态一步预测误差方差阵；

其中，Q为状态方程噪声w的协方差阵。

步骤3：计算滤波增益矩阵；

其中，R为观测方程噪声v的协方差阵。

步骤4：校正预估值更新滤波状态；

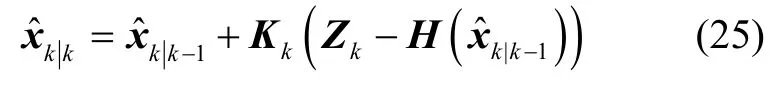
步骤5：更新状态估计误差方差阵。

3 雷达误差干扰及延时补偿

捷联主动雷达工作时受硬件采集、软件信息处理等过程影响，探测输出角度存在指向误差、测量噪声、测角量化、雷达波束扫描范围限制、输出延时等一系列误差干扰，如图4所示。

图4 雷达探测误差干扰Fig.4 Disturbance of radar detection

由于雷达信息传递及计算处理比较耗时，测量输出延迟特性会造成控制系统中雷达探测信息与惯组测量信息出现时频特性不一致不匹配的现象，影响最终指标精度，可根据雷达测量输出信息中的时戳延迟在信息融合时将惯组信息进行同等延时补偿，实现雷达与惯组信息的同步性。

假设收到雷达探测信息的时刻为t，雷达信息延迟时间为td，即利用t-td时刻的惯组姿态信息、t时刻的雷达测角信息解算t时刻的视线角及视线角速度并输出。

其中，h(·) 表征解算函数。

捷联主动雷达解耦得到视线角及角速度后，可采用比较常规的比例导引进行制导解算。

其中，视线角及角速度信息λD、、来自第2 节卡尔曼滤波解耦结果。kth、kla、ksi为制导系数，Tg为剩余飞行时间，θD为约束落角，、为速度方向变化率。

4 仿真验证

基于本文给出的设计方法，在飞行末段主动雷达识别捕获目标后转入雷达跟踪，雷达测量噪声假设为高斯白噪声，测距标准差取2.0 m，测速标准差取0.7 m/s，测角标准差取0.2°，角度量化分辨率取0.02°，输出时间延迟取40 ms，终端入射余角（落角约束）取60°，雷达转目标跟踪时扩展卡尔曼滤波状态量初值在线解算并赋值。

标称状态目标系解耦六自由度仿真结果与惯性系解耦及无卡尔曼滤波结果对比曲线如图5-10所示，图中Tdec 表征本文目标系解耦设计方法，Adec 表征本文模型下惯性系解耦方法[8]。

图5 雷达探测视线角Fig.5 Detection angles of radar

图5两种解耦方法下雷达探测视线角的差异主要是惯性系解耦加入落角补偿造成的。图6与图7中惯性系解耦所构建的视线角及角速度要明显大于目标系解耦值，尽管对最终的落点精度影响不大，但在过载需求上更严苛一些，从图10的过载曲线可以反映出来。图8、图9两种方法视线角及角速度滤波均能较好的收敛，惯性系角速度估计误差初值比目标系偏大是由于惯性系落角补偿后视线角前期变化偏快导致。

图6 解耦后视线角Fig.6 LOS angles after decoupling

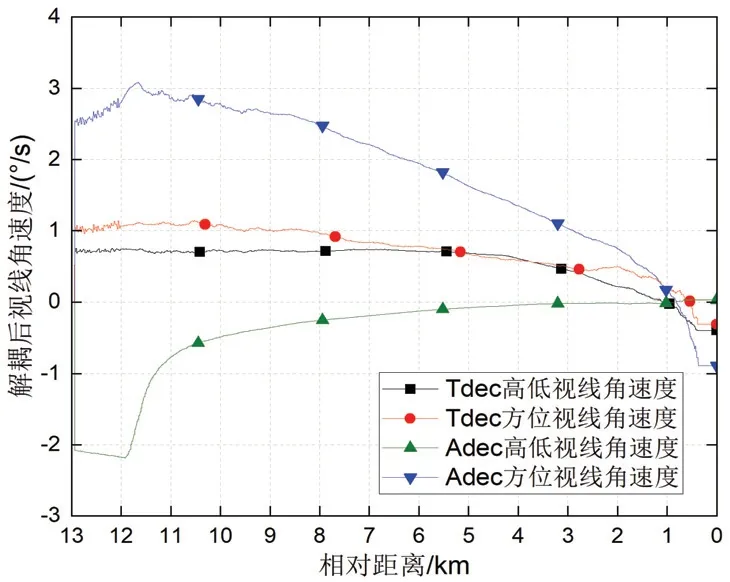
图7 解耦后视线角速度Fig.7 LOS angular rates after decoupling

图8 视线角滤波估计误差Fig.8 Estimation error of LOS angles

图9 视线角速度滤波估计误差Fig.9 Estimation error of LOS angular rates

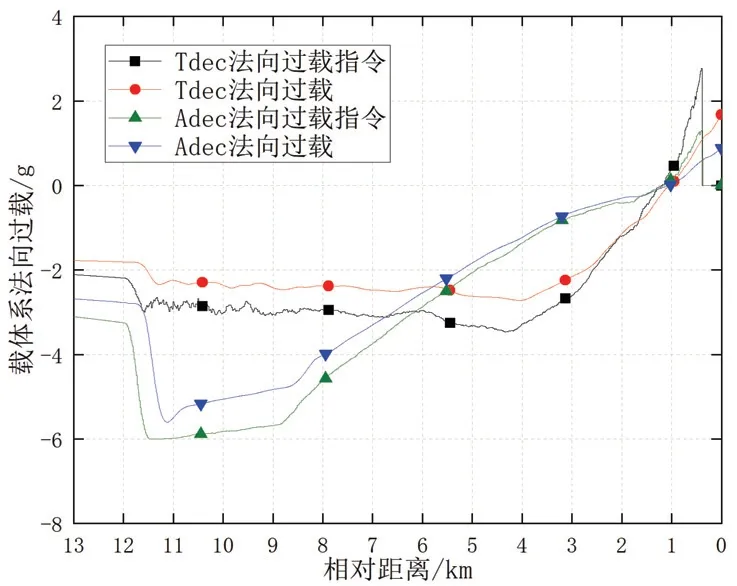
图10 载体系法向过载Fig.10 Normal overload of body coordinate

为进一步确认本文目标系解耦方法在扰动状态下的适应性，同时探究单项措施对最终结果的影响，考虑飞行环境、动力等偏差因素进行模拟打靶，以本文方法仿真结果为基线，将不加延时补偿、不加扩展卡尔曼滤波（差分法）、惯性系解耦三类方法结果相对于基线进行比较，具体如表1所示。

表1 打靶结果相对基线比较Tab.1 Comparison of shooting results

从表1数据可以看到，本文采取的扩展卡尔曼滤波、延时补偿等措施都能有效提高终端指标精度，且滤波对终端指标的有利影响更大。仿真结果中目标系解耦方法相对惯性系解耦在脱靶量指标上有提高但量级不大，在落角改善上优势明显，均值与期望角度60°的偏差缩小了2.8°（(60-54.28)-(60-57.08)=2.8），落角精度提升超过40%（2.8/(60-54.28)=0.48），尤其末段飞行侧向机动增大时效果更突出，且不需要根据目标距离进行落角修正，对比数据验证了本文方法正确有效。