基于仿射近似投影模型的无人机对地目标定位方法

孙 聪，贾萌娜，于起峰

（1.西安卫星测控中心 宇航动力学国家重点实验室，西安 710043；2.中国空间技术研究院西安分院，西安 710000；3.国防科技大学 空天科学学院，长沙 410073）

随着计算机、人工智能、微电子以及数字通信等相关技术的迅猛发展，无人机（Unmanned Aerial Vehicle,UAV）综合性能不断提高，具有机动灵活、实时高效、成本低廉等诸多优势，目前已广泛应用于昼夜空中侦查、战场监视、战损毁伤评估、边境巡逻等军事领域以及航空摄影、地球物理勘探、土地资源调查、灾情监测、林业普查等民用领域，显现出重大的军事、经济和社会效益[1]。鉴于无人机对目标的定位精度直接影响其综合性能的发挥，特别是针对战场环境下的大倾角、小交会角等典型弱观测几何条件，研究无人机对地面目标的高精度定位方法具有重要意义。

无人机平台对地面目标定位就是利用机载传感器采集的多源数据综合处理得到待测目标在指定坐标系下的精确三维坐标，根据是否主动发射辐射大体可分为有源定位和无源定位方法。鉴于有源定位方法隐蔽性弱，且定位精度高度依赖于机载传感器的定向和测距精度，以景象匹配[2]、地形轮廓匹配[3]、多视图三维重建[4]为代表的无源定位方法越来越受到重视。考虑到景象匹配或地形匹配方法需要预先制备基准图或地形高程数据，基于无人机序列影像的稀疏三维重构方法更成为当前研究热点[5]。

针对序列影像的稀疏三维重构，增量式运动恢复结构方法（SFM,Structure from Motion）计算代价大、对初始重建敏感且难以避免误差累积；而基于运动平均思想的全局式SFM 在求解全局一致位置时易存在解算不稳定、对粗差点敏感及陷入局部最优等瓶颈[6]。相较之下，因子分解法同等考虑所有视图及特征，能够平衡所有图像数据误差，且为各向同性零均值高斯噪声下的极大似然重建。同时考虑到本文处理对象为无人机平台对地目标的远景成像环境，采用透视投影模型不仅无助于提高位姿求解精度，而且由于成像模型存在过参数化问题，数值求解鲁棒性较差。

基于此，本文提出了基于仿射近似投影模型的无人机对地面目标定位方法。该方法在迭代因子分解法的框架下，采用平行透视投影模型替代透视投影模型对无人机序列成像过程进行建模，利用序列影像特征的多视图几何约束实现目标区域的高精度三维重构，并充分利用机载导航系统提供的高精度相机位置信息，进而完成对地面目标的精确定位。此外，为进一步增强因子分解法的精度和鲁棒性，本文采用了基于优化最小化的低秩矩阵分解方法。最后，通过数值仿真和半实物仿真试验检验了所提方法的综合性能。

1 无人机对地面目标定位基本原理

1.1 问题描述

无人机平台对地面目标序列成像如图1所示，假定在j（j=1,2...k）时刻，地面特征点Pi（i=1,2...n）投影至像面Ij于点pi（i=1,2...n），令光心坐标为Cj（j=1,2...k）。则无人机平台对目标定位问题可描述为，已知世界坐标系OXW YW ZW下各时刻相机成像位置Cj以及该时刻下像面特征点坐标pi，解算相机在各时刻的相机光轴指向Rj∈SO（3）以及地面特征点三维坐标。

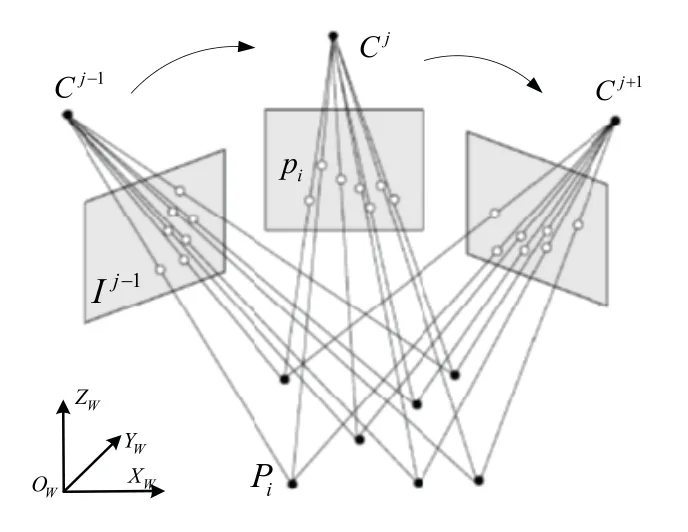
图1 特征点多视图几何约束Fig.1 Multi-view geometric constraints of feature points

1.2 求解方法

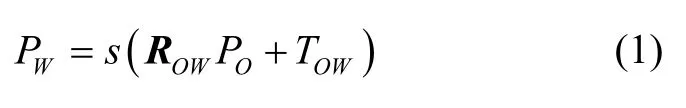
其中（s,ROW,TOW）分别表示欧式坐标系OXO YO ZO至世界坐标系OXW YW ZW相似变换的尺度、相对旋转矩阵以及平移向量。鉴于相机光心坐标可由高精度GPS 提供，即可认为已知，求解上述相似变换即可转化为绝对定向问题。

易知当存在至少k≥ 3非共线相机光心坐标时，可获得绝对定向问题唯一解。文献[7]进一步给出了式(2)求解的最小配置条件。基于计算得到的相似变换参数，便可得到待测目标在世界坐标系下三维坐标。

2 基于仿射近似投影模型的因子分解法

本文采用平行透视投影模型对无人机远景成像过程进行建模，进一步基于仿射近似投影模型下的迭代因子分解法框架[8]，结合最新低秩矩阵恢复算法[9]，实现对无人机序列影像的高精度鲁棒重构，并最终通过透视投影模型下的光束法平差优化相机运动参数及目标三维点坐标。

2.1 平行透视投影模型

平行透视投影模型可看作两次投影过程的合成，即目标先沿着光心与质心G(Xg,Yg,Zg)的连线平行投影至目标质心平面，再根据透视成像模型投影至实际成像面，投影矩阵为[8]：

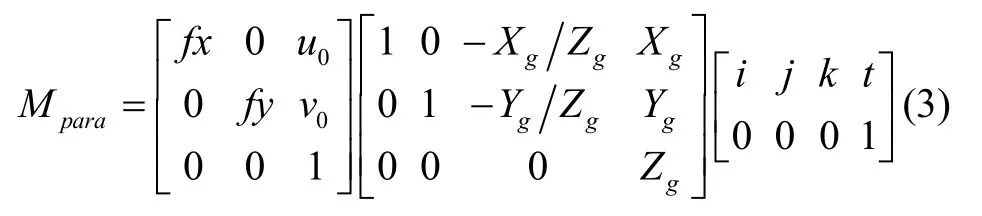
其中(fx,fy)为相机横纵方向等效焦距，(u0,v0)为像面主点坐标。令此外令表示目标质心的像面坐标，并定义表示目标点PW到质心G所在平面的距离与质心深度的比值。

则平行透视投影模型可改写为：

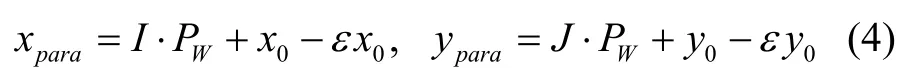
而透视投影模型可表示为：

综合式(4)(5)，可知两投影模型存在如下约束，

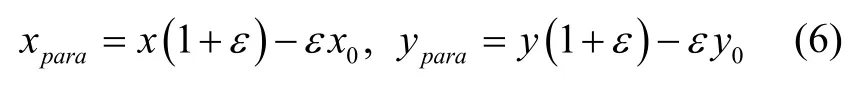
分析可知平行透视投影相当于透视投影的一阶近似，即使在ε取值较大时，可通过选取合适的原点G（x0,y0）即可对平行透视模型进行补偿，进而提供良好的透视模型近似。

2.2 因子分解法

因子分解法基本思想是根据多视图间特征轨迹组成测量矩阵的秩约束，利用奇异值分解将测量矩阵分解为相机运动矩阵和目标三维结构矩阵。如图2所示，考虑包含n个特征点的k幅图像序列，特征点像面坐标为wij=（xij,yij）T（i=1...n;j=1...k），假定目标结构由其体坐标系下的三维特征点为｛Pi,i=1...n｝，令Rj,tj=（tjx,tjy,tjz）T分别表示目标坐标系下相机姿态矩阵与位置向量，则视图k中特征点i在相机坐标系下坐标为Pij=Rj Pi+tj，进一步根据平行透视投影模型投影至像面[10]，

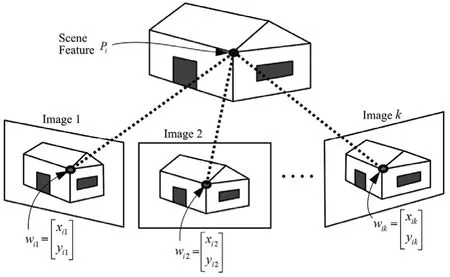
图2 序列图像中的特征轨迹Fig.2 Feature tracked in an image sequence

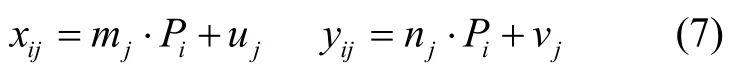
其中，Rj=（ij,jj,kj）T，

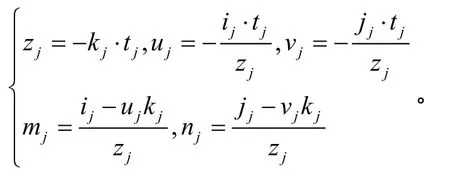
考虑同个目标点的k个不同视图，假定多视图间的特征对应关系已经建立，根据式(7)将所有视图及特征联立为矩阵方程，

或简写为：

根据图像数据可直接计算得到，

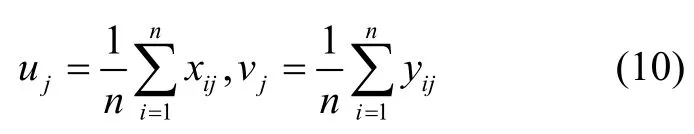
进而对式(9)进行重心化，即可得到：

分析易知理想情况下该测量矩阵的秩rank(W*) ≤ 3，但由于测量中不可避免存在的噪声，可以定义如下代价函数，

文献[10]给出了目标函数的详细求解方法，同时S.Christy[8]指出由于矩阵分解的歧义极易导致相机位姿的镜像模糊，极大地影响相机位姿参数估计的精度和鲁棒性，需要采用合理的方式进行消除。

2.3 基于平行透视投影模型的迭代因子分解法

如图3所示，迭代因子分解法的基本思想是增量式地估计εij的值，进而逐步修正透视投影模型下的像面投影直至与平行透视投影下投影重合，因而可以将透视重建简化为迭代平行透视投影重建。该框架在保持高度线性化的优势同时，最大限度近似透视投影效果，且能够妥善解决传统仿射近似投影模型下因子分解法存在的位姿模糊问题。

图3 平行透视投影模型下的迭代因子分解法Fig.3 Iterative factorization under paraperspective model

再次考虑如式(5)所示的透视投影模型，

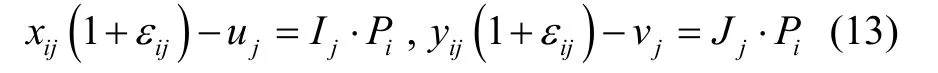
以及式(6)的平行透视投影模型，

该算法框架主要步骤如下：

(1) 初始化，∀i,ji∈ ｛1...n｝，j∈ ｛1...k｝，令εij=0；

(2) 根据式(14)更新像点观测值sij；

(3) 基于平行透视投影模型进行三维重构[10]；

(4) 基于式 (14)，对 ∀i,ji∈ ｛1...n｝，j∈ ｛1...k｝，重新估计εij；

(5) 判断当前迭代的εij值与前次迭代值差值是否在给定阈值内，若满足阈值则停止迭代，结果输出，反之则返回步骤(2)。

为剔除位姿模糊，定义非奇异矩阵H，使得L=GH，则有Q=LLT=GHHTGT=GGT。

易知H必然为正交矩阵，H表示了一个旋转或者镜像变换，对应存在两组可能的目标结构。鉴于目标结构在相差一个旋转变换下确定，不失一般性地将镜像变换定义为-I（I 为单位阵）。因此仿射运动恢复结构矩阵方程可表示为：W=MS=（-M）（-S）。对应地，重建算法每次迭代的εij存在两解。可根据IP、JP（正解）或-IP、-JP（负解）计算得到两个不同的解k1j和k2j，其对应的εij为：

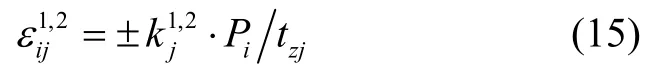
重建算法每次迭代计算过程中得到两解，N次迭代后便可得到2N个可能的解。但很明显并不是所有解均能与图像数据符合，可通过一个简单的验证策略以避免解的维数爆炸。即实际上每次迭代仅保留两个可能的正、负结构直至收敛，最后再根据与图像数据符合的程度选取唯一解，文献[8]结果表明通常仅需3-5 次迭代便可收敛。

2.4 基于优化最小化的低秩矩阵分解方法

在相机序列成像过程中，由于视场改变、目标遮挡、光照变化等因素不可避免地导致部分特征点不可持续观测或跟踪失败，体现在观测矩阵W中便是存在特征数据缺失和粗差点。奇异值分解法能给出如式(12)所示L2范数下各向同性零均值高斯噪声下的极大似然解，但面对于实际测量环境中更为复杂的误差模型以及不可避免存在的数据缺失、粗差点，奇异值分解法将难以适用，因而本节将采用更为鲁棒的L1范数进行求解。鉴于L1范数的非凸性和非光滑性，本节采用基于优化最小化（Majorization-Minimization,MM）的低秩矩阵鲁棒分解方法[9]，该方法计算精度高，具有较好的鲁棒性和可扩展性，且无需准确初值就能收敛至全局最优。

2.4.1 优化最小化

优化最小化基本思想是，针对于一个非凸或不光滑的目标函数h（x），不直接对该目标函数优化求解，转而在当前迭代解xk处构建容易处理的替代函数f（x,xk），通过对替代函数迭代优化求解逼近目标函数的最优解[9]。基于每次迭代所求的解构造新一次迭代的替代函数，并根据新的替代函数优化求解得到下一次迭代的求解，直至无限逼近于目标函数的最优解。

如图4所示，替代函数f（x,xk）曲线位于目标函数曲线h（x）上方，则其应满足约束，

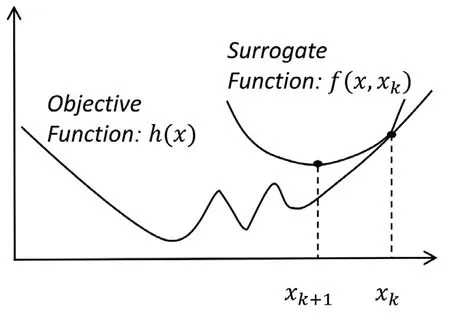
图4 优化最小化算法原理[9]Fig.4 Illustration of majorization-minimization[9]

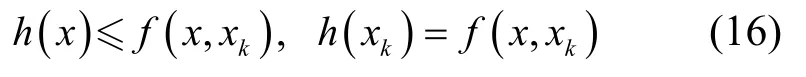
并通过对函数f（x,xk）最小化求解获得xk+1，

因此有：

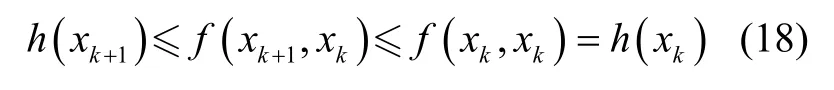
由式(18)可知，在迭代优化替代函数f（x,xk）的过程中，也在不断地优化目标函数h（x），即保证目标函数的值是单调非增的。

2.4.2 测量矩阵低秩分解

考虑到测量矩阵中不可避免存在的数据缺失，式(12)可进一步建模为[9]，

其中W∈Rm×n为秩为r（r≪min（m,n））的测量矩阵，为矩阵L1范数，M∈Rm×r，S∈Rn×r为未知的低秩分解矩阵。而Φ 为与测量矩阵W同尺寸的二进制掩模矩阵，输入值为0 表示W中相同位置元素缺失，否则为1，运算符⊙表示矩阵元素哈达玛乘积。

为进一步降低求解复杂度，施加如下约束，

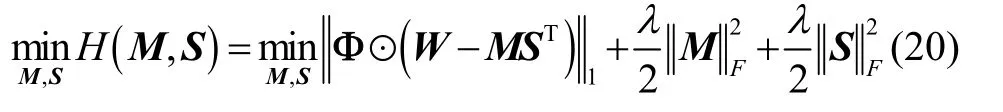
其中，λ∈ R+为正则因子。此外，对于任意秩小于或等于r的矩阵X，存在等式，

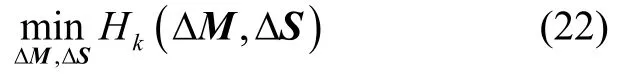
其中，

即现在目标是寻找使得目标函数保持单调递减的增量（ΔM,ΔS），但方程(22)求解并不容易，因而可基于MM 框架，采用一个方便求解的凸函数代替。基于范数的三角不等式可得，

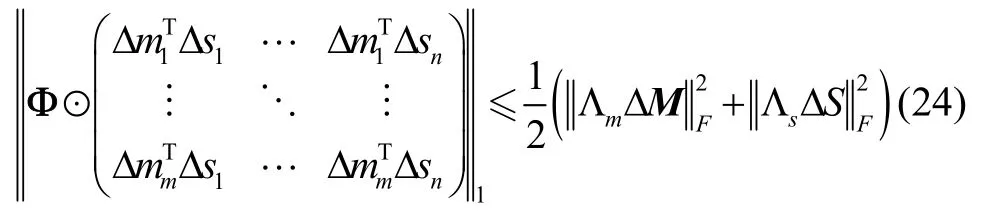
其中，Λm，Λs为对角矩阵，Λm的第i个对角元素为其中 #Φ（i,.）为掩模矩阵Φ 中第i行非零个数，ζ为任意正尺度因子。类似地，Λs的第j个对角元素为而 # Φ（.,j）为掩模矩阵Φ 中第j列非零个数，当且仅当（ΔM,ΔS）=（0,0）时，式(24)才相等。

进而可得到关于Hk（ΔM,ΔS）的松弛函数[9]，

其中，

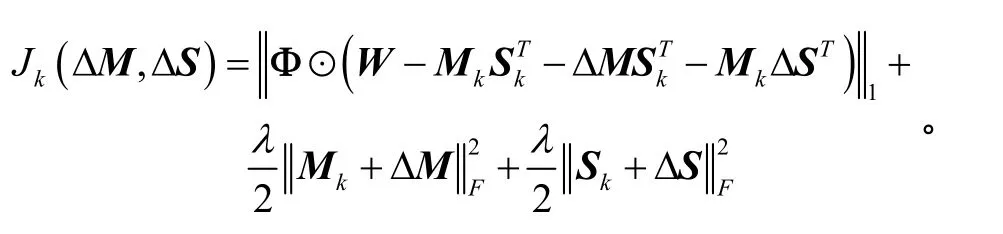
综合式(23)-(25)可知Fk（ΔM,ΔS）满足约束(16)，说明Fk（ΔM,ΔS）可作为原目标函数Hk（ΔM,ΔS）的替代函数。此外，Fk（ΔM,ΔS）是拥有唯一最优解（ΔMk,ΔSk）的强凸函数，则原始目标函数H（M,S）也是单调非增的，当目标函数改进值小于给定阈值时停止迭代。该强凸函数可转化为分离结构线性约束凸优化问题，进而可采用基于并行分裂和自适应惩罚的线性交换方向乘子法（LADMPSAP）完成求解[9]。

2.5 算法总结

算法输入：无人机机载相机获取的目标序列影像；

Step 1:图像预处理，组成目标特征测量矩阵W；

Step 2:初始化，∀i,i∈ ｛1...n｝，∀j,j∈ ｛1...k｝，令εij=0；

Step 3:根据式(14)更新像点观测值sij；

Step 4:基于平行透视投影模型进行三维重构；

a.基于优化最小化框架下的低秩矩阵分解方法，对测量矩阵W分解获得相机运动矩阵M以及目标结构形状矩阵S；

b.基于姿态矩阵的正交性约束，考虑仿射重建的位姿模糊，首次迭代可获得正、负目标结构S（1）,R（1）(R（1）=-S（1）)；

Step 5:基于式(15)，对 ∀i,i∈ ｛1...n｝，∀j,j∈ ｛1...k｝，每次迭代可获得对应于正、负结构的εij各两解

Step 6:判断当前εij值与前次迭代值差值是否满足给定阈值，若满足则停止迭代，反之则返回Step 3；

Step 7:结果输出，迭代收敛时获得对应于正、负结构的两解，根据与原始图像数据的符合程度选取唯一解作为重建结果输出。

Step 8:透视投影模型下迭代优化。为进一步提高重建结构的精度，降低仿射模型的近似误差，在透视投影模型下，对迭代因子分解法获取的相机运动参数以及目标三维点坐标进行光束法平差优化。

3 试验与分析

3.1 仿真试验

仿真试验模拟无人机针对地面目标远距离绕飞模式，设置无人机距离地面目标 12 km，绕飞高度3 km，目标点随机分布于边长为350 m 的立方区域内。默认设置机载相机分辨率1000 pixel ×1000 pixel，视场角为3°×3°。仿真试验主要考核相机姿态角误差、定位误差、绕飞交会角、特征点数、视图数目以及像点误差等典型因素影响下算法精度。试验主要对比算法为：

直接交会算法：即传统的基于视线直接交会的目标定位方法；

透视+BA：文献[7]中采用机载导航系统输出的相机高精度位置为约束，基于透视投影模型下的光束平差法解算获得地面目标的定位方法；

仿射+BA：即本文提出的基于仿射近似模型的无人机对地定位方法。

3.1.1 姿态角误差对定位精度影响

仿真实验首先以相机姿态误差作为主变量，变化区间为[0～0.1°]，步长0.01°，检验了典型交会角(10°,30°,50°)、以及图像数目(10,30,50)等因素对于定位精度的影响，结果如图5所示。

而综合分析图5(a)可知，在观测视图数较少时，“透视+BA”和“仿射+BA”两种方法定位误差均相对较大，在拥有足够的特征或视图数时，再继续增加视图数目对于定位精度提升效果不明显，这也可为实际测量任务提供指导。

从图5(b)可知，在交会角极小(10°)时，采用“透视+BA”或“仿射+BA”方法的定位误差较大，究其原因是观测几何呈现极度病态，采用非线性迭代优化进一步使得结果偏离真值。而当交会角较大时，两种方法精度明显高于直接交会法，且两方法定位精度差异较小。观察图5(c)可知，“透视+BA”和“仿射+BA”两种方法的定位误差随像点噪声增大而变大，且在当前仿真配置下，两种方法定位精度基本一致。

由图5(a)-(c)可知，典型测量条件下直接交会定位误差随姿态角误差增大而近似线性增大，而“透视+BA”和“仿射+BA”两种方法基于相机高精度位置信息约束，大幅度降低了对于高精度定姿设备的依赖，在当前配置下两种方法的定位精度几乎不受姿态角误差增大影响。进一步可以观察到，在姿态角误差小于0.03°时，直接交会法的精度优于“透视+BA”和“仿射+BA”两种方法，这也从侧面反映了在当前配置下本文提出方法的精度提升上限。

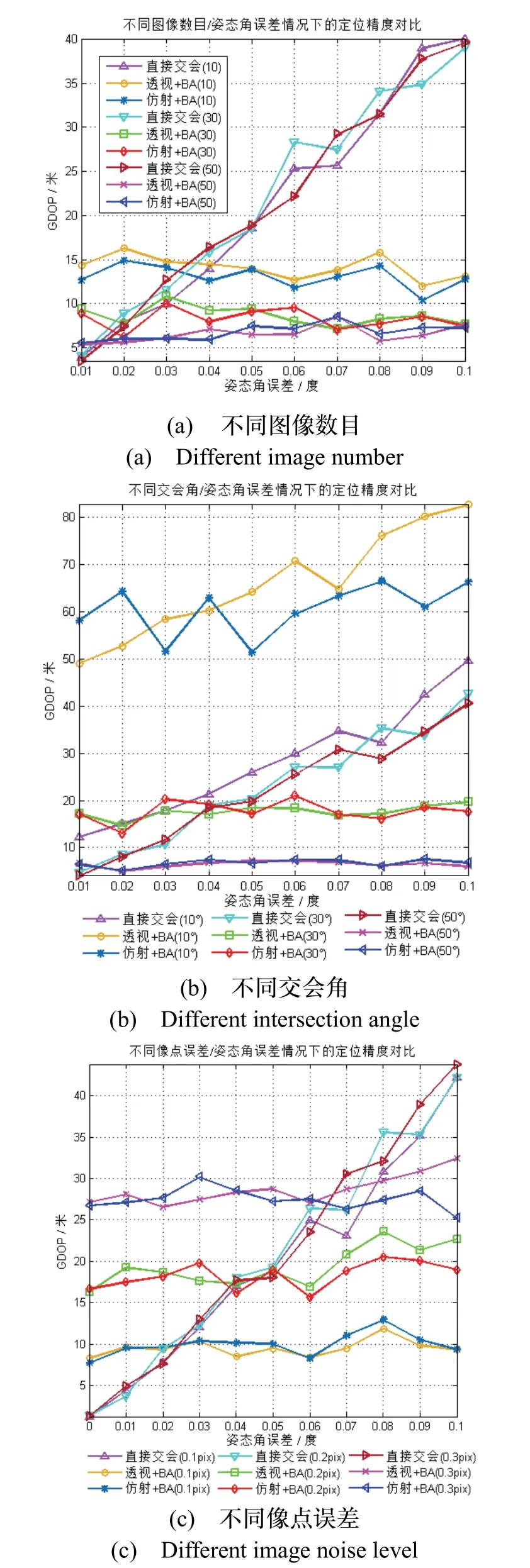
图5 不同姿态角误差条件下三种定位方法精度对比Fig.5 The accuracy comparison of three positioning methods under different attitude errors

3.1.2 交会角大小对定位精度影响

前述试验结果显示，直接交会法在默认姿态角误差条件下定位精度较差，故接下来的实验中并未以其作为算法性能评估参照。本实验检验交会角以步长10°在区间[10°～90°]变化时，典型相机定位误差、像点误差等因素对于定位精度的影响，实验结果如图6所示。

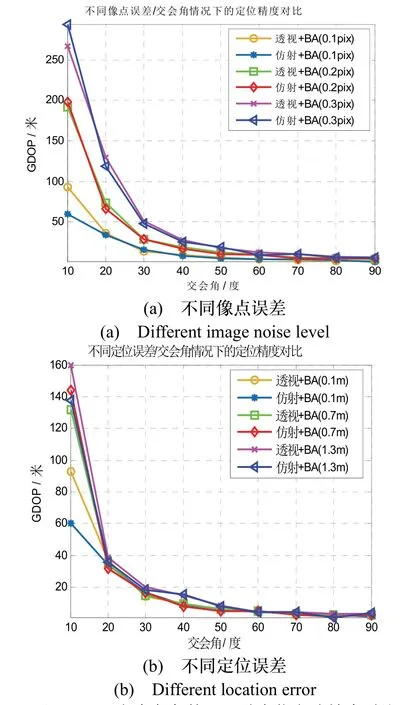
图6 不同交会角条件下两种定位方法精度对比Fig.6 The accuracy comparison of two methods under different intersection angles

随着交会角增大，不同因素影响下的定位方法误差均逐渐降低直至平稳。在交会角较小(≤50°)时，成像几何病态性显现，两方法针对像点误差、定位误差以及特征点数等影响因素较为敏感，而随着交会角增大至 ≥60°时，以上诸因素的影响效应大幅度降低，说明交会角是影响算法定位精度的重要决定因素。另从图6(b)可知，相机位置误差的增大并未给定位精度带来明显影响，也进一步说明本文采用的基于高精度位置约束的对地定位方法的有效性。高精度的像点提取、相机位置信息、足够的目标特征以及观测视图是保证高精度目标定位的基本前提。

3.1.3 像点噪声对定位精度影响

本试验进一步检验不同像点噪声水平下，典型交会角以及特征点数目条件下不同方法的定位性能对比。像点噪声变化区间为[0.1～1.0]像素，步长0.1 像素。精度对比结果如图7所示。

由图7可知，随着像点噪声增大，两种定位方法的误差均随之增大。其中，如图7(a)所示，在交会角较大时，两种方法的误差曲线增长趋势均较缓，且二者差异不明显，而当交会角较小(20°)时，误差增长更为剧烈，且采用“透视+BA”方法误差相对较大。类似的变化趋势也体现在图7(b)中，在特征点数较为充足的条件下，两种方法误差曲线基本重叠，而当特征点数较少(10)时，“透视+BA”方法的定位精度相对较低。

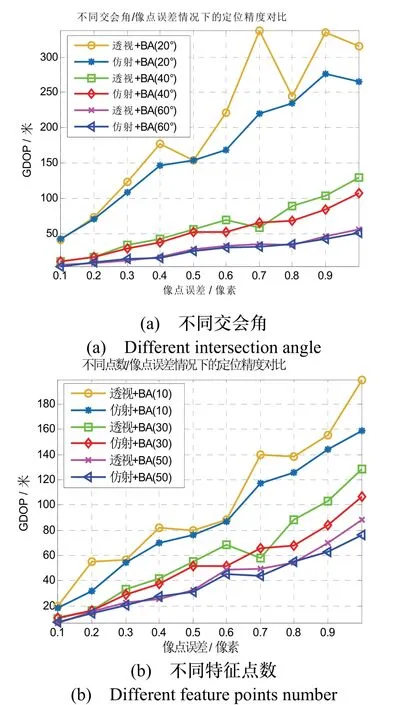
图7 不同像点噪声水平下两种定位方法精度对比Fig.7 The accuracy comparison of two methods under different image noise level

试验结果说明像点噪声同样是影响定位精度的重要因素，在实际测量任务中应尽可能提高特征提取与匹配的精度。同时，也进一步说明本文提出的“仿射+BA”对地定位方法正确有效，且在弱观测几何条件下，相较于“透视+BA”方法，精度和鲁棒性更优。

3.2 半实物仿真试验

为进一步验证本文提出方法的性能，在实验室受控条件下进行了半实物仿真试验，如图8所示。

图8 无人机对地目标定位半实物仿真实验布置图Fig.8 The semi-physical simulation experimental setup of Geo-targeting with unmaned aerial vehicle

试验中采用推车搭载相机在一定高度对于模拟沙盘上的目标区域近似绕飞模式连续成像，全序列图像视线交会角约为40°。实验中采用Imperx CCD 相机(分辨率：2456 pixel ×2058 pixel)，焦距50 mm 的Kowa 透镜。

利用全站仪测量目标区域放置的若干黑白对角标志的三维坐标，并采用现有成熟位姿估计算法计算各采样时刻相机的位置和姿态。以解算得到的位置模拟无人机导航信息，在估计得到的相机姿态基础上叠加均值为0.2 像素，标准差0.05 像素的高斯噪声作为定向信息输入。

3.2.1 特征跟踪结果

序列图像特征高精度提取与跟踪是其用于后续三维重建的基本前提与重要保障，特别是针对于无人机远景成像条件，特征提取与跟踪过程中的微小误差将随着成像距离的增大而剧烈放大，因而本文引入基于扩展卡尔曼滤波的目标跟踪框架[11]，利用目标区域静态三维场景的结构约束，进而实现目标特征的高精度稳定跟踪。

试验共采集 443 帧序列图像（采样频率约10 fps），选择21 个黑白对角标志，采用基于扩展卡尔曼滤波的点目标特征跟踪方法完成序列图像中的特征跟踪，结果如图9所示。

图9 序列图像特征跟踪结果Fig.9 Feature tracked in the image sequence

选定特征在全序列图像中均能稳定跟踪，特别是在如075帧、205帧、396帧等由于相机视场变化，部分特征超出视场无法观测时，基于扩展卡尔曼滤波框架的跟踪算法仍可预测目标特征可能的位置，且当目标特征再入视场时可迅速完成捕获，体现了该跟踪方法在本实验中的良好性能，也为进一步高精度目标定位奠定基础。

3.2.2 对地目标定位结果

基于序列图像的特征跟踪结果，分别采用“直接交会法”、“透视+BA”以及“仿射+BA”三种目标定位方法进行解算，并以全站仪测量值为参考检验算法精度。首先以间隔10 帧选取全序列共44 帧图像，采用三种方法解算得到的定位结果如图10所示，统计各定位结果相对于参考值的解算误差如表1所示。

表1 基于全序列影像(采样间隔10)的目标定位误差Tab.1 The geo-targeting error based on full sequence images(sampling interval 10)

图10 基于不同方法的定位结果Fig.10 The geo-targeting results of different methods

如图10所示，采用“透视+BA”或“仿射+BA”解算得到的目标特征点三维坐标与参考值吻合较好，而直接交会法误差相对较大，说明采用位置信息强约束可以明显提高对地定位精度，也反映了本文提出算法正确有效。

由表1可知，在当前配置下采用“透视+BA”或“仿射+BA”方法获得的定位误差均值和中误差均明显低于直接交会方法，且“透视+BA”或“仿射+BA”两种方法的定位误差较为接近。

为进一步考核两种方法的综合性能，分别进行如下实验：

1）以间隔20选取全序列共22帧图像进行解算，结果如表2所示；

表2 基于全序列影像(采样间隔20)的目标定位误差Tab.2 The geo-targeting error based on full sequence images(sampling interval 20)

2）以间隔10 选取前半序列共22 帧图像进行解算，结果如表3所示；

表3 基于前半全序列影像(采样间隔10)的目标定位误差Tab.3 The geo-targeting error based on the first half of whole sequence images(sampling interval 10)

3）以间隔10 选取全序列共44 帧图像，并设置15%序列特征像点随机缺失，解算结果如表4所示。

表4 基于15%特征随机缺失的全序列影像(采样间隔10)的目标定位误差Tab.4 The geo-targeting error based on full sequence images(sampling interval 10) with 15% random deletion of features

分析表2易知，当采样间隔增大，用于解算的视图数目减半时采用直接交会法的定位误差有所增大，而另外两种方法的定位精度未发生明显改变，说明在当前配置下，采样22 帧不同视图已足以完成高精度的目标定位信息解算，进一步增加解算视图对于定位精度没有明显改善。

而根据表3可观察，当仅采用前半序列，即观测交会角减半时，三种方法的定位误差均随之上升，其中直接交会法定位误差增加的最为剧烈，“透视+BA”法次之，而本文提出的“仿射+BA”方法最小，说明本文方法在较小的交会角下性能更好，定位精度和鲁棒性更优。

进一步观察表4可知，当存在部分观测数据缺失时，采用直接交会法或“透视+BA”法的定位误差均有不同幅度的增大，而“仿射+BA”方法的定位误差仅小幅增加，进一步说明本文方法具有较强的鲁棒性，可以较好地适应于实际的工程测量环境。

4 结 论

针对无人机对地目标远景成像时采用透视投影模型存在过参数化的问题，本文提出了基于仿射近似投影模型的无人机对地面目标定位方法。在基于平行透视投影模型的迭代因子分解法框架下，利用无人机序列影像，结合基于扩展卡尔曼滤波的点目标跟踪方法以及基于优化最小化框架的低秩矩阵分解技术，实现了剔除位姿模糊歧义的目标区域高精度欧式三维重构，再充分利用机载导航系统提供的高精度相机位置信息，即可完成对地面目标的精确定位。该方法摆脱了对高精度定姿IMU 以及地面控制点的依赖，使得基于低成本硬件设备实现对地面目标高精度定位成为可能。仿真和半实物仿真试验结果显示，本文提出的基于仿射近似投影模型的无人机对地面目标定位方法正确有效，实验室环境下对地目标定位精度优于2 厘米。