基于变分贝叶斯优化的近邻采样PF-SLAM算法

袁 帅，刘同健，栾方军，张 凤，吴 健

（1.沈阳建筑大学 电气与控制工程学院，沈阳 110168；2.沈阳建筑大学 计算机科学与工程学院，沈阳 110168）

自主导航是移动机器人的关键技术，同时定位与建图(Simultaneous Localization and Mapping,SLAM）用于有效建立环境地图与描述机器人位姿状态，是移动机器人自主导航的前提[1]。粒子滤波（Particle Filter,PF）SLAM 算法解决在完全未知环境下移动机器人SLAM 问题。由于PF-SLAM 算法迭代会出现粒子权重衰退现象，采用重采样的优胜劣汰方法改善该问题后，又导致了粒子多样性丧失问题[2]。此外传统SLAM方法都是基于观测噪声已知的前提，若此前提不成立，即观测噪声未知或突变时，传统SLAM 算法性能会受到极大影响。

针对PF-SLAM 算法中粒子多样性丧失的问题，文献[3]将粒子群方法引入到无迹粒子滤波SLAM 中，提高了粒子多样性及系统状态估计精度。文献[4]采用遗传算法中交叉变异方法，解决PF 粒子多样性丧失问题。文献[5]采用布谷鸟算法优化重采样方法，将粒子引导至高似然区域，提高了算法精度。文献[6]模拟萤火虫群体的生存机制优化重采样过程，解决粒子多样性丧失问题。文献[7]采用排挤机制和启发式蝙蝠算法，通过引入惯性权重提高了粒子多样性。针对SLAM问题中的时变观测噪声，文献[8]采用残差和信息序列的正交原则对观测噪声进行实时调整，但计算复杂度高，无法满足系统实时性。文献[9]提出多个并行滤波器近似真实噪声的多模型自适应算法，实际运行中需要知道传感器的精确误差特性，难度较大且不易实现。近年来，变分贝叶斯的机器学习方法[10]因其计算量低、时效好的优势，被广泛应用于SLAM 算法中。文献[11]采用线性变分贝叶斯方法对SLAM问题中地图特征和噪声方差进行迭代更新。文献[12]利用变分贝叶斯方法对移动机器人状态和未知观测噪声参数的联合后验概率进行估计，解决观测噪声参数未知或变化时，传统滤波算法出现的滤波发散问题。

在上述研究工作基础上，本论文提出基于变分贝叶斯的近邻采样PF-SLAM 算法（Variational Bayesian Adjacent Sampling-Particle Filter-Simultaneous Localization and Mapping,VBAS-PF-SLAM），采用高斯混合模型对时变观测噪声建模，利用变分贝叶斯循环迭代方式估算未知参数分布，处理时变观测噪声；参考高权重保留粒子，通过近邻位置关系优化低权重调整粒子的位置分布，避免重采样过程中粒子退化现象，同时提高粒子多样性，使得粒子更好地表示机器人位置概率分布。仿真实验结果表明本文提出的算法保证了实时性且有效提高移动机器人同时定位与建图的精度。

1 移动机器人PF-SLAM 算法

移动机器人驱动模型与观测模型如下：

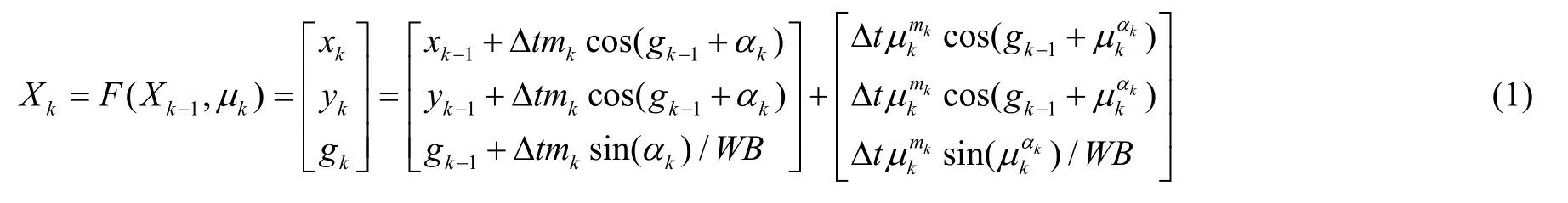
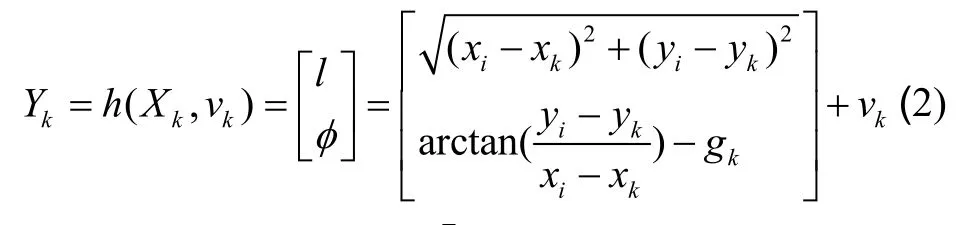
式中Xk=（xk,yk,gk）T为k时刻机器人状态向量，xk、yk、gk为移动机器人在二维正交坐标系下的位置和朝向信息，xi、yi为环境路标的位置信息，μk为零均值、Qk为高斯白噪声的协方差，为速度噪声，为转向角噪声，mk,αk为机器人控制变量，其中mk为机器人移动速度，αk为机器人前轮相对于机器人底座偏转角度。Δt为传感器采样时间间隔，WB为前后轮间轴距。观测模型中l为机器人与环境路标之间激光传感器测量距离，φ为机器人朝向与环境路标夹角，机器人朝向由惯性传感器解算后获得，vk为观测噪声（包括时变与时不变两种情况的观测噪声）。

假设已知1:k时刻机器人状态信息、环境观测信息、机器人控制信息与环境路标信息，则机器人SLAM问题就可看成求解后验概率分布问题。

传统粒子滤波SLAM算法使用里程计数据和传感器观测信息作为重要性建议分布，从中采样得到粒子，对机器人位姿状态和路标进行估计。算法步骤如下：

Step 1：重要性采样：建议分布中采样得到N个初始粒子；

Step 2：粒子权重计算：根据当前时刻机器人观测信息更新粒子权值；

Step 3：粒子重采样：淘汰小权重粒子、复制大权重粒子并归一化新粒子；

Step 4：定位与建图：根据粒子分布信息与传感器观测数据估计机器人位姿状态并构建环境地图；

Step 5：机器人运行至下一时刻，根据驱动模型获得新的粒子分布，返回至Step 2 循环运行。

2 基于变分贝叶斯优化的时变观测噪声估计

2.1 时变观测噪声建模

传统SLAM方法采用单高斯分布拟合时不变观测噪声，理论上能够取得精确估计结果。时不变观测噪声的单高斯多维随机变量X服从分布描述为：

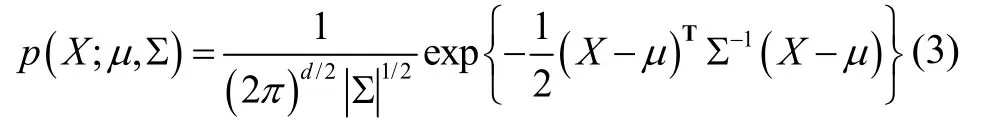
式中X表示维度为d的随机列向量，μ为均值，Σ 为协方差。

然而在实际SLAM场景中，移动机器人平台抖动、周边环境干扰及传感器存在噪声等问题会造成机器人移动模型观测噪声参数变化，这种情况下传统滤波方法不能调节观测噪声参数会导致SLAM精度下降或发散。考虑到实际环境存在多个噪声来源，单高斯分布无法描述这种情况，所以本文采用高斯混合模型表示时变观测噪声[13]。

高斯混合模型作为高斯分量的简单线性叠加能够提供比单高斯分布更丰富的时变噪声扰动，进而可以更准确描述多个来源的噪声概率分布，提高移动机器人SLAM 估计精度。图1为采用单高斯分布曲线近似表示混合高斯分布时变噪声的示意图，图中红色曲线近似表示时变观测噪声分布，蓝色曲线为多个单高斯分布拟合的高斯混合模型。

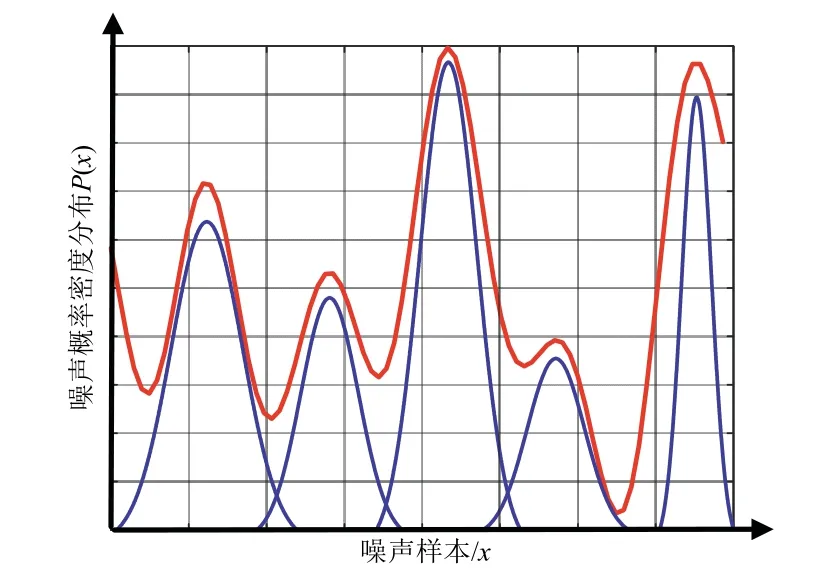
图1 时变噪声分布示意图Fig.1 Time-varying noise distribution diagram

在采用高斯混合模型对时变观测噪声建模后，通过变分贝叶斯学习方法估算混合模型的未知参数分布，解决未知或突变观测噪声产生的状态发散问题。

使用多个单高斯分布加权和近似表示时变观测噪声vk，得到高斯混合模型：

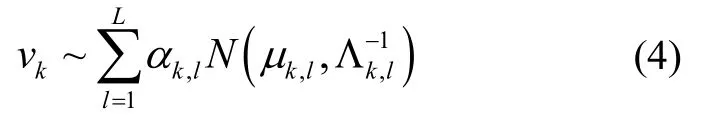
式中L为单高斯分布个数，αk,l为k时刻高斯项l的系数，μk,l为高斯分布均值，为协方差。设有S个观测噪声样本，隐变量Z表示为S×L的矩阵，将上述参数与隐变量Z统一为噪声参数集合ψk=［αk,μk,Λk,Z］。

为估计观测噪声参数，假设高斯混合模型的先验分布为Gauss-Wishart 分布：

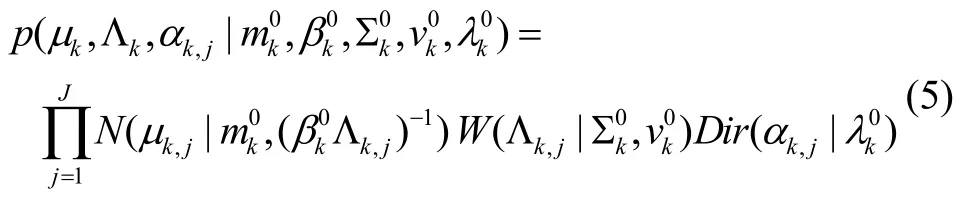
采用变分贝叶斯方法[14]迭代估计高斯混合模型中未知噪声参数的超参数 Σ,ν,m,β,λ，进而获得时变观测噪声参数估计值。

2.2 高斯混合模型噪声参数估计

通过驱动模型与观测数据推断系统状态及未知噪声参数。假设系统状态与未知噪声参数后验分布为：

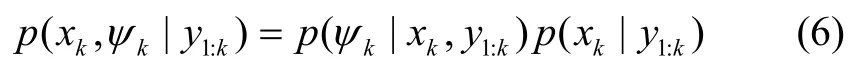
由于ψk的表示形式复杂，难以直接估计噪声参数的真实后验分布p(ψk|xk,y1:k)，根据变分近似思想，引入易处理的分布q(ψk)近似真实后验分布。假设基于变分贝叶斯学习模型的对数边缘似然函数为：

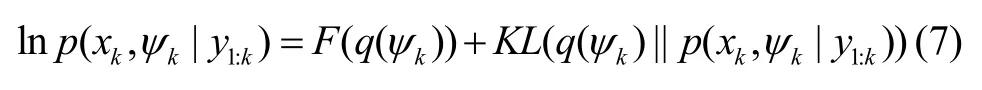
式中KL(q(ψk)||p(xk,ψk|y1:k))为KL散度，用来描述q(ψk)与p(ψk|xk,y1:k)真实分布的差距，F(q(ψk))为变分自由能。考虑到式(7)左边值恒定，当q(ψk)与真实分布p(ψk|xk,y1:k)充分接近时，KL散度最小，F(q(ψk))最大。变分贝叶斯方法通过对q(ψk)进行迭代，使得变分自由能F(q(ψk))最大化，即获得最小KL散度。

通过平均场理论，将联合概率分布近似为多变量概率分布函数的乘积，q(ψk)可分解为：

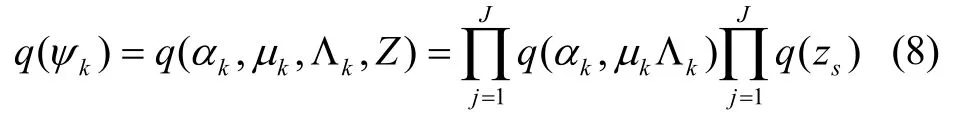
式中隐变量Z的近似后验分布为q(Z)及噪声参数的近似联合后验分布q(αk,μk,Λk)通过坐标上升迭代方法求解[15]，得到：

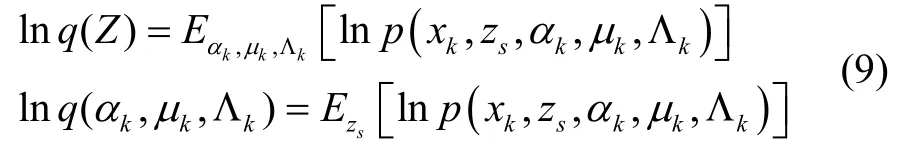
将式(9)转化为：

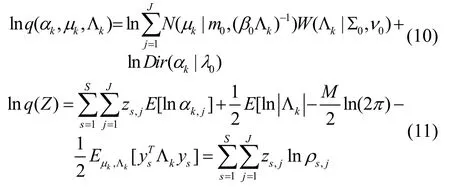
式中超参数β,m,Σ,ν,λ更新公式如下：

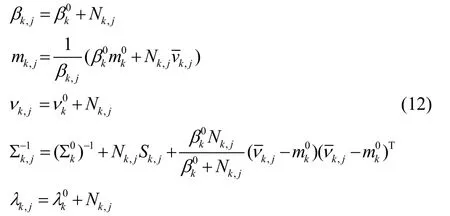
对于式(12)的中间变量定义为：

式中γs,j为式(11)隐变量Z后验分布归一化常数：

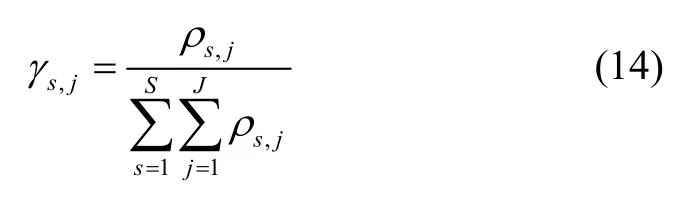
通过式(12)(13)迭代更新超参数的值，每次迭代后计算变分自由能并计算：

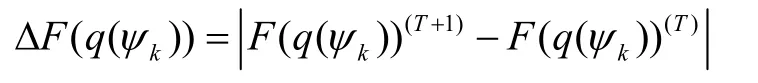
当ΔF小于阈值τ时即认为变分自由能最大化，此时q(ψk)与真实分布接近，进而获得时变观测噪声的参数估计值。

3 基于近邻采样的PF-SLAM 算法

传统PF-SLAM 算法引入重采样方法解决迭代过程中权值退化问题时会出现粒子多样性丧失问题，并且重采样后的粒子位置分布也影响了机器人位姿估计精度。本文提出基于近邻采样的 PF-SLAM 算法(AS-PF-SLAM)过程分为以下三步：基于近邻位置关系的粒子采样、采样粒子位置优化、构建新的粒子集。

3.1 基于近邻位置关系的粒子采样

将传统重采样后的粒子集分为高权重粒子保留组与低权重粒子调整组，根据近邻位置关系对调整组粒子采样，使用较少数量的粒子分布，覆盖调整组粒子分布区域，优化粒子位置分布，增强粒子多样性。

3.1.1 重采样粒子数量计算

根据采样粒子的维度，计算其近邻粒子数量，例如维度为1、2 维的情况下，其近邻粒子数量分别2、4，进一步推广到dim维情况下的近邻粒子数量为2*dim。在粒子采样中，由采样粒子代表其近邻粒子的概率密度分布。调整组中粒子采样数量为(dim为粒子维度)： 调整组粒子数/2*dim+1。

3.1.2 近邻位置关系的计算

样本点Xi与样本空间中其它点Xj的近邻关系由欧式距离来衡量。距离公式如下：

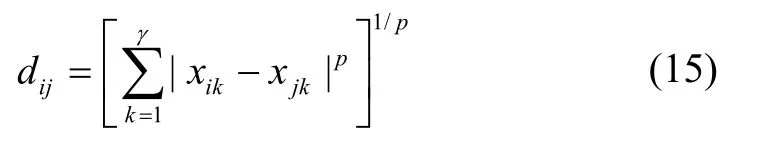
式中k为样本点的维度分量，当p=2时，表示欧式距离；欧式距离可以简单有效地反映两点之间位置拓扑关系，计算复杂度小，更符合本文要求。

3.1.3 粒子采样过程

Step 1：传统的重采样方法对粒子集合Sk重采样，获得重采样集合SA，将SA集合中的高权重粒子构成保留组SGH，未选入SA中的Sk其他粒子构成调整组SGA，粒子数为NGA；

Step 2：在保留组SGH中寻找权重最高的粒子Pm，根据近邻位置关系寻找调整组中距离Pm最远粒子Ps1，对该粒子位置进行优化（详见采样粒子位置优化部分）得到P's1，将其加入到采样组SGS；同时搜寻Ps1的2*dim邻近粒子，将邻近粒子与Ps1从调整组中删除；

Step 3：将上一步中优化的P's1放在调整组中，类似于Step 2 的处理过程，寻找当前调整组中距离P's1最远的粒子Ps2，对该粒子位置优化（详见采样粒子位置优化部分）得到P's2，将其加入采样组SGS；同时搜寻Ps2的2*dim邻近粒子，将这些邻近粒子与Ps2从调整组中删除。对以后的粒子重复Step 2 的过程，直至调整组中粒子数量低于2*dim+1，获得SGS中粒子个数为

3.2 采样粒子位置优化

传统重采样没有考虑粒子位置分布对机器人估计精度的影响。本文根据粒子权重将粒子划分为权重较小的调整粒子Psj与权重较大的保留粒子Pam。通过近邻位置关系，找到距离调整点最近的2*dim个保留点Pam，比较近邻保留点Pam的权重大小，选择最高权重的近邻保留点，通过式(16)计算调整点Psj的位置：

式中，randn是介于(0,1)区间的正态分布随机数，（1-abs（randn）/step）为学习因子，其中step为randn随机数向最优粒子位置逼近程度，取值为3σ(σ为randn标准差)，Psj为调整点位置，Pam为调整粒子附近权重最大的保留粒子位置。

3.3 构建重采样粒子集

重构SGS与SA为重采样粒子集S'A，集合粒子个数为N，与重采样前Sk的元素个数相同。SA是由传统重采样方法产生的高权重粒子集，缺乏粒子多样性且未考虑粒子位置分布对机器人概率分布的影响。因此，本算法将SA去掉M个粒子后，再与SGS一起构成新的粒子集S'A。为了降低计算量，可以采用确定性重采样方法在SA中选择去掉的粒子。

4 基于变分贝叶斯优化近邻采样PF-SLAM 算法

将变分贝叶斯粒子滤波方法与近邻采样粒子滤波算法结合，提出基于变分贝叶斯优化的近邻采样PF-SLAM 算法（VBAS-PF-SLAM），处理时变观测噪声的同时提高了粒子多样性和系统估计精度。图2为VBAS-PF-SLAM 算法流程图，具体算法步骤如下：

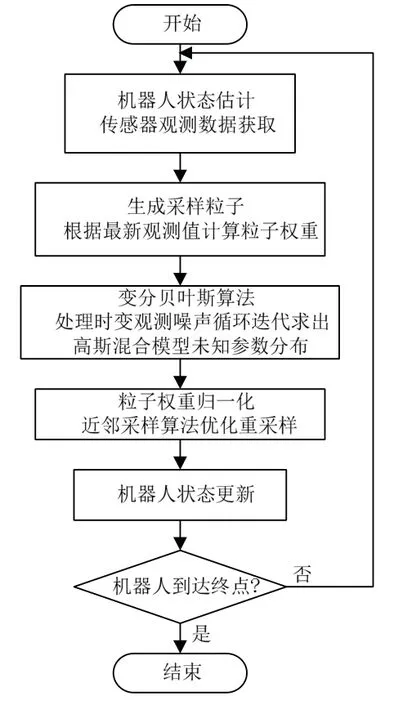
图2 基于变分贝叶斯优化的近邻采样PF-SLAM 流程图Fig.2 Flow chart of adjacent sampling PF-SLAM algorithm based on variational Bayesian optimization

1) 初始化概率密度函数p(x0)，使用高斯混合模型近似时变观测噪声，产生初始粒子；初始化高斯混合模型未知参数的超参数。

2) 在建议分布中采样N个粒子，从状态方程中得到先验概率：

3) 机器人状态估计：传感器获取观测数据并根据观测值计算粒子权重ωki：

4) 使用变分贝叶斯方法[14]循环迭代地求出混合模型中未知参数分布。

5) 针对权重退化及粒子多样性丧失问题，采用近邻

采样算法改进重采样，步骤如下：

① 按式(15)计算粒子间近邻位置关系并采样。

② 按式(16)对采样后的粒子位置分布进行优化。

③ 位置优化后的粒子与原重采样粒子重构成新的粒子集。

6) 判断机器人是否到达终点，对2)～5)步骤进行迭代操作。

5 仿真实验与分析

5.1 移动机器人SLAM 仿真实验环境

图3为仿真实验环境，图中绿色十字、米字符和红色米字符分别代表135 个随机设定的特征点位置、机器人运动的17 个路标点和机器人估计的特征点位置，用于描述机器人同时定位与地图构建中传感器扫描的环境特征，折线为机器人预定前进路线。移动机器人SLAM 仿真参数设定：机器人移动速度为3 m/s，激光雷达传感器探测距离为0～30 m，探测范围为360°。机器人控制信号时间间隔为0.025 s，噪声参数维度为二维，高斯混合模型设定由5个单高斯分布构成L=5，取迭代阈值为 ΔF＜10-8时迭代停止，机器人系统噪声为μk=diag[（0.1m）2,（π/180）2]，时不变观测噪声协方差为vk=diag[（0.1m）2,0.0552]，参考该值设置时变观测噪声协方差，使得二者数量级相同，粒子集中粒子个数为100，图中黑色椭圆为机器人位姿估计时的粒子群放大图，由100 个蓝色圆点组成。

图3 机器人定位与建图仿真结果Fig.3 Simulation results of robot localization and mapping

5.2 基于近邻采样的 PF-SLAM 算法（AS-PF-SLAM）验证

5.2.1 本算法对传统重采样算法改进效果对比

将近邻采样算法（AS）与15 种传统重采样方法应用于零均值单高斯分布模拟观测噪声的机器人定位与建图中，分析近邻采样算法对15 种传统重采样方法改进前后的移动机器人位置估计均方根误差(Root Mean Square Error,RMSE)。

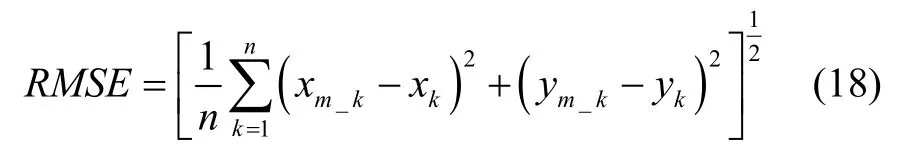
式中（xm_k,ym_k）为机器人真实位置，（xk,yk）为机器人估计位置，n为机器人迭代次数。

如图4所示，蓝色条形统计为15 种传统重采样算法的机器人位置估计均方根误差，橙色条形统计为近邻采样算法的机器人位置估计均方根误差。仿真数据表明，通过近邻采样算法改进后的重采样算法将机器人位置估计均方根误差平均降低了36.14%，证明本算法能够有效提高PF-SLAM 精度，且具有通用性。

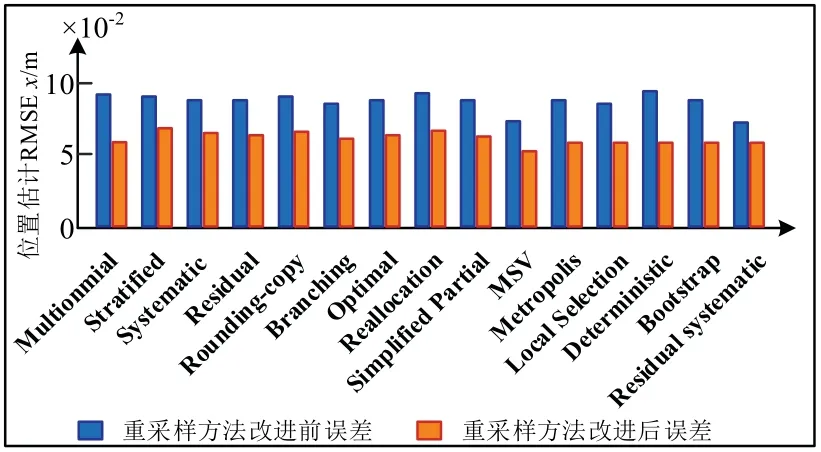
图4 本算法对传统重采样算法改进效果对比Fig.4 This algorithm compares the improvement effect of traditional resampling algorithm

5.2.2 本算法与基于蝙蝠算法、粒子群算法的PF-SLAM 仿真对比

图5为 AS-PF-SLAM 算法与基于粒子群PF-SLAM 算法（PSO-PF-SLAM）、基于蝙蝠算法的PF-SLAM（BA-PF-SLAM）的PF-SLAM 粒子位置分布及粒子多样性对比图。图5(a)为移动机器人初始粒子分布图，即机器人在初始时刻确定自身位置，但没有确定自身朝向角。图5(b)为通过外部传感器观测后的粒子分布图，即机器人运动较短距离后，考虑自身朝向角不确定性，粒子向周身360°范围内扩散，再根据传感器观测值对粒子群进行粒子权重系数评估（高、低权重粒子）的位置分布。

针对传统重采样方法未考虑粒子位置分布对滤波精度的影响以及粒子多样性丧失现象。AS 算法通过粒子间近邻拓扑位置关系将低权重粒子保留并趋近于近邻高权重粒子，如图5(c)所示，使得粒子位置分布更接近机器人概率分布。图5(d)为AS-PF-SLAM 算法优化后的新粒子集，其具有更好的粒子位置分布及粒子多样性，进而提高移动机器人SLAM 精度。

粒子群优化算法(PSO)效仿鸟群交流特征进行粒子采样寻找全局最优解。图5(e)为PSO-PF-SLAM 算法粒子位置优化图，粒子在搜索空间中单独搜寻局部最优粒子和全局最优粒子，使其位置向高权重粒子靠近。与AS 算法位置优化方式相比，PSO 算法中无法寻到最优位置的低权重粒子直接淘汰，图5(f)为PSO算法粒子集。

蝙蝠算法（BA）效仿蝙蝠觅食的回声定位方式进行粒子采样，在个体速度与位置基础上增加频率和声波，利于粒子跳出局部最优，提高运算效率并增加粒子多样性。图5(g)为BA-PF-SLAM 算法粒子位置优化图，低权重粒子向最优粒子移动、高权重粒子进行方向不定的随机移动。相比于PSO-PF-SLAM 算法，BA-PF-SLAM 算法的低权重粒子随着高权重粒子的随机移动易于摆脱局部极值吸引，使趋近全局最优的粒子增多，但距离高权重粒子较远的其他粒子仍会被淘汰。图5(h)为BA-PF-SLAM 算法的粒子集。

图5 多种算法优化的粒子位置分布及多样性对比图Fig.5 Particle distribution and diversity comparison of multiple algorithms optimization

综上所述，AS-PF-SLAM 算法通过粒子间近邻拓扑位置关系，将低权重粒子趋近高权重的粒子位置，稳定且保留了更多采样粒子，优化粒子位置分布的同时进一步提高了粒子多样性，使粒子更均匀的分布在可能区域内，在真实位置附近的权重较大且复制数量较多，保证了最优位置的估计精度。

采用零均值单高斯分布模拟观测噪声进行仿真对比，结果如图6所示，以机器人运行迭代次数为横坐标、机器人位置估计误差为纵坐标，在相同仿真环境下，对比传统 PF-SLAM 算法（黑色线条）、PSO-PF-SLAM 算法（绿色线条）、BA-PF-SLAM 算法（蓝色线条）与AS-PF-SLAM 算法（红色线条）的移动机器人位置估计误差。

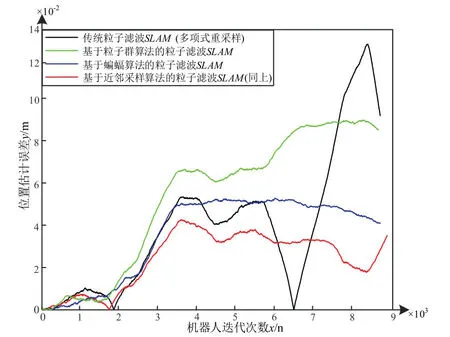
图6 单高斯噪声下多PF-SLAM 算法定位误差对比Fig.6 Comparison of positioning errors of multiple PF-SLAM algorithms under single Gaussian noise

仿真数据表明，基于AS-PF-SLAM 算法的机器人位置估计精度较PSO-PF-SLAM、BA-PF-SLAM 算法的位置估计精度平均提升了27.36%。证明了本算法对于移动机器人同时定位与地图构建的鲁棒性增强有明显效果。

5.3 基于变分贝叶斯优化的近邻采样PF-SLAM 算法验证

采用高斯混合模型模拟时变观测噪声，进行仿真对比，图7为在相同仿真环境下对比传统PF-SLAM、基于期望最大化算法（EM）的PF-SLAM 算法、VB-PF-SLAM 算法及VBAS-PF-SLAM 算法的移动机器人位置估计误差曲线。其中黑色线条代表PF-SLAM算法的位置估计误差；绿色线条代表EM-PF-SLAM 算法的位置估计误差；红色线条代表VB-PF-SLAM 算法的位置估计误差；蓝色线条代表VBAS-PF-SLAM 算法的位置估计误差。

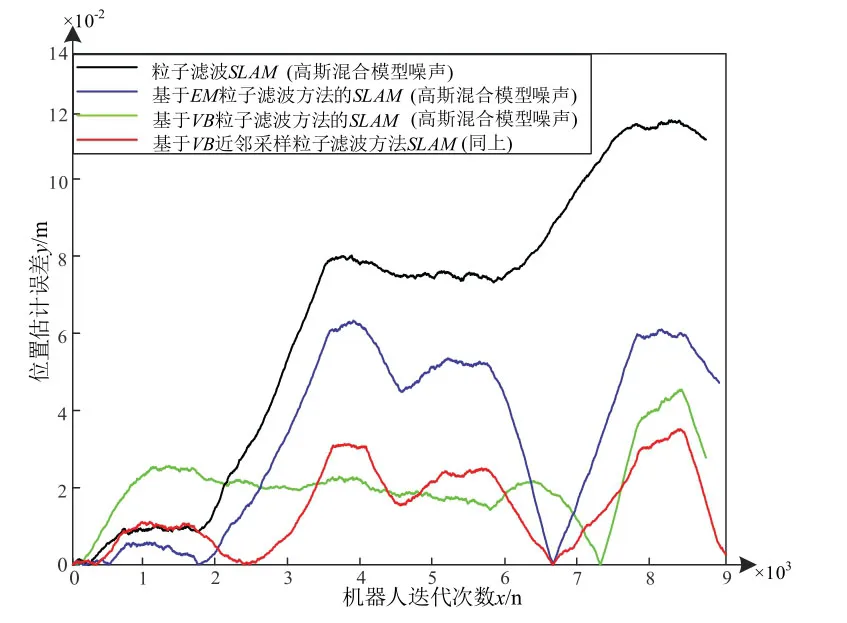
图7 混合高斯噪声下多PF-SLAM 算法定位误差对比Fig.7 Comparison of positioning errors of multiple PF-SLAM algorithms under mixed Gaussian noise

仿真数据表明，VBAS-PF-SLAM 算法的机器人位置估计精度较传统PF-SLAM 算法精度提升了76%，较EM-PF-SLAM 算法提升了54%，较VB-PF-SLAM算法提升了33%，保证算法实时性的同时，显著提升了机器人同时定位与建图精度。

6 结 论

针对传统PF-SLAM 算法中粒子多样性易丧失及传感器观测噪声时变问题，本文提出基于变分贝叶斯优化的近邻采样PF-SLAM算法，优化粒子位置分布，并增强粒子多样性，使得粒子更好地表示机器人概率分布。采用高斯混合模型对时变观测噪声建模，利用变分贝叶斯方法迭代计算混合模型中未知参数分布，处理时变观测噪声，提高移动机器人SLAM估计精度。

实验结果表明，本算法与PSO 算法、BA 算法相比，具有更高精度与时效性，且对传统重采样算法改进具有通用性。在观测噪声时变情况下，本算法显著提高了机器人定位与建图精度，对解决未知环境中的移动机器人定位与地图构建问题具有一定指导意义。