连采机吸尘风筒振动特性分析
2022-06-09闫红红张宏王晓波
付 政,闫红红,张宏,王晓波
(太原科技大学 机械工程学院,太原 030024)
煤矿掘进工作面一直是井下粉尘主要产生场所,对于连采工作面主要用机载除尘系统来进行降尘。吸尘风筒是连续采煤机除尘系统的主要组成部分,风筒在内部流体力作用下,可能会产生振动和变形,振动会在采掘巷道产生强烈的噪声,从而影响井下从业人员的工作状态和身体健康[1]。
国内外学者主要通过理论解析[2]、实验测试[3]和数值模拟[4-6]对管道振动进行研究。Lee[7]等根据管道的振动方程和流体方程,提出流固耦合方程,以研究管道的稳定性和动力响应。谢安桓[8]等研究人员建立液压管道流固耦合三维模型,运用谐响应分析方法,探讨不同影响因素下的管道振动响应特性。张晋春[9]等建立筒装料管道模型,利用有限元分析软件ANSYS12.0对管道车内部流场进行流固耦合模拟。马青[10]等人利用Hamilton原理推导出采空区埋地管线横线振动方程,并研究管内气体压力造成流固耦合带来的振动影响。
当前,流固耦合的研究主要集中在直管及一些三通管,而吸尘风筒的内部流动较为复杂,相关研究较少。本文通过建立连采机吸尘风筒的有限元模型,利用Workbench进行风筒的模态和振动特性仿真,并对吸尘风筒的动态响应结果进行分析,探究风筒的工作振动情况。
1 流固耦合数学模型
吸尘风筒内的流体可以看作是不可压缩的流动。风筒中流体的质量守恒、能量守恒和动量守恒构成流体控制方程,即雷诺平均Navier-Stokes方程[11],即表达式为:
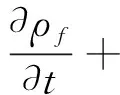
(1)

(2)

(3)

(4)
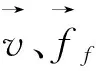
固体域的基本控制方程由下式所示:
ρsds=∇·(∂s)+fs
(5)
式中:ρs、∂s、fs分别为风筒的密度、欧拉应力张量和体积力矢量;ds为当地加速度矢量。
风筒结构和内部流体两个物理场满足流量q、温度T、位移d和应力τ等变量守恒时,则流固耦合面上的方程为:
(6)
2 几何模型建立及模态分析
2.1 几何模型建立
图1所示为连续采煤机机载前端吸尘风筒三维模型。吸尘风筒与连续采煤机截割臂相连接,分布着A、B、C三组不同面积大小的条缝型通孔,截割臂的运动可带动吸尘风筒的升降。A、B两组吸尘口分别设置在吸尘风筒的左右两侧,而C组吸尘口分布在中部输送装置的上方,与各组吸尘口相连三条通道由导流板隔开,各自独立。

图1 吸尘风筒结构示意图Fig.1 Structure diagram of vacuuming ram
2.2 模态分析
采用Ansys Workbench中的Meshing对风筒的流体域和固体域分别进行四面体网格划分,流场计算设置为Realizable k-ε进行求解,壁面函数为Non-Equilibrium Wall Functions.针对不同流体流速和流体压强进行风筒内部流场数值模拟计算。将流体分析的结果经流固耦合面施加到固体域,并利用静力学模块和模态模块进行流固耦合计算和模态分析。在模态分析中,风筒内的流体运动会影响风筒结构的固有频率,本文只求解风筒的前六阶固有频率大小和振型分布。
3 结果分析与讨论
3.1 风筒模态分析
风筒结构在空管和单向流固耦合状态下会存在差别。设置三组吸尘口流体速度为5 m/s和风筒流体压强为340 Pa,进行流体动力学计算,将结构流场载荷传递到固体域,进行预应力下模态分析。吸尘风筒的空管、单向流固耦合两种状态下得到的固有频率分别用I和II来表示,结果如表1所示。
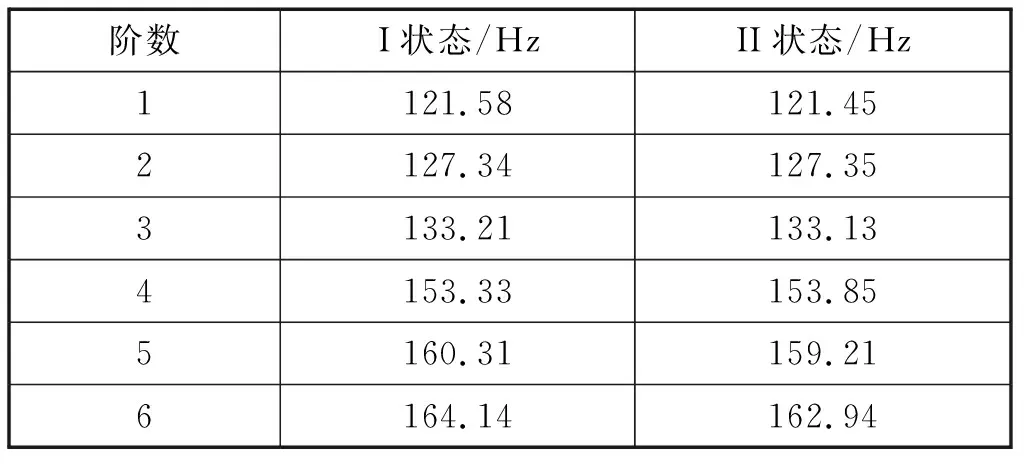
表1 吸尘风筒的固有频率Tab.1 Natural frequency of vacuuming ram
由表1可以看出,随着振动阶数的增加,风筒的固有频率也同样增长。空管状态与流固耦合状态有着相似的频率变化趋势,前3阶风筒的固有频率数值变化不大,从第3阶到第6阶,固有频率值明显增加。流固耦合状态下的吸尘风筒,第2阶和第4阶的固有频率大于空管道的固有频率,其他阶数频率与空管相比,下降趋势明显,说明流固耦合作会降低风筒的固有频率。
图2所示为两种状态下第1、2、3阶吸尘风筒的振型图。从中可以看出,在同一阶次比较下,I和II两种状态的振型幅值大致接近,且振幅分布位置相似,流固耦合状态下的最大振幅值20.486 mm,最小振幅值为8.800 7 mm,由此可见流体对吸尘管道的振动存在影响,但是影响作用不大。

图2 不同状态下的前三阶振型Fig.2 The first three-order modes under different states
3.2 不同流体速度对风筒的影响
在速度分别为5 m/s,7 m/s,9 m/s和11 m/s时,吸尘风筒的固有频率如表2所示,由表可知,随着气流速度的增加,风筒的固有频率也相应的增加;当流速为11 m/s的第6阶固有频率与流速为5 m/s的第6阶固有频率之间的值仅相差0.69%.说明在比较相同阶次下,气流速度的变化不会引起风筒的固有频率的大幅度增加。

表2 不同流速下的吸尘风筒前6阶固有频率Tab.2 The first 6-order natural frequencies of vacuuming ram at different flow rates
不同流速下风筒的总变形和等效应力如图3所示,当吸尘口速度为11 m/s时,吸尘风筒的变形量和等效应力最大,最大应变值和最大应力值分别为 0.195 31 mm和2.133 5 MPa.可以发现,吸尘风筒结构在右端管道和汇流管道处,出现了大幅度的变形区域和应力集中区域;随着吸尘口速度的增加,风筒的应力值与应变值也相应增加。

图3 不同流速下的吸尘风筒的总变形和等效应力图Fig.3 Total deformation and isostatic effect diagram of vacuuming ram at different flow rates
3.3 流体压强对吸尘风筒的影响
在风流速度为5 m/s情况下,计算流体压强分别为140 Pa,340 Pa,540 Pa,740 Pa时的吸尘风筒固有频率,得到前六阶固有频率如表3所示。在第3阶中,压强为740 Pa下频率值仅仅比压强为140 Pa下的频率值增加了0.07 Hz,说明随着流体压强的增加,各阶次的固有频率值也小幅度的增加,但对风筒的固有频率影响不大。

表3 不同流体压强下吸尘风筒前6阶固有频率Tab.3 The first 6-order natural frequencies of vacuuming ram at different fluid pressures
图4为不同压强下的总变形和等效应力图,气流压强为740 Pa时的最大变形量比气流压强为140 Pa时的最大变形量增加了0.031 4 mm.由此可知,气流压强的增加对风筒的变形量的变化影响较小;风筒的右端管道和汇流管道壁面均出现了高应力区域和明显的变形区域,并呈现出相同的变化规律。

图4 不同流体压强下的吸尘风筒的总变形和等效应力图Fig.4 Total deformation and isostatic effect diagram of vacuuming ram under different fluid pressure
3.4 谐响应分析
根据流固耦合作用下的风筒模态分析结果,采用模态叠加法(Mode Superposition)对吸尘风筒进行谐响应求解并分析,得到风筒在不同频率下的动态响应曲线如图5所示。
在图5(a)位移谐响应曲线中,y方向上的最大位移幅值为0.092 6 mm,而x、z方向无明显峰值出现;图5(b)加速度谐响应曲线中,y方向上的最大加速度幅值为6.372 5×104mm·s-2,而x、z方向曲线平缓,无明显峰值出现;图5(c)应力谐响应曲线中,z方向上的应力响应峰值明显大于x、y方向,最大应力响应峰值为0.352 MPa,;图5(d)应变响应曲线中,z方向上的应变响应峰值明显大于x、y方向,最大应变响应峰值为1.58×10-6mm/mm.


图5 振动特性响应曲线Fig.5 Response curve of vibration characteristics
从图5(a)-图5(d)中可以看出,随着激励频率的增加,位移、加速度、应力与应变响应曲线趋势基本一致,均在约130 Hz周围出现了峰值。
4 结论
(1)吸尘风筒在单向流固耦合作用下,使得各阶固有频率值略有减小,与空管状态比较,相应阶次的振幅幅值变化不大,各阶振型基本相似。
(2)流体压强和流体速度的变化对吸尘风筒的固有频率影响较小。风筒的右端管道和汇流管道处出现了大幅度的变形区域和应力集中区域。随着流体压强和流体速度的增加,风筒的应力值与应变值也相应增加。
(3)通过对结构最大变形区域进行谐响应分析,根据振动特性响应曲线变化规律,吸尘风筒在z方向上振动位移和加速度最大,在y方向上应力应变最大,当激励频率为130 Hz时出现峰值,容易出现共振现象。
