耦合太阳能的冷热电联供系统双层运行优化配置设计
2022-06-09谭钧元郑非凡
谭钧元,王 旭,许 野,李 薇,郑非凡
(1.华北电力大学环境科学与工程学院,北京 102206;2.华北电力大学核科学与工程学院,北京 102206)
天然气冷热电联供系统作为环境友好型和资源节约型的能源形式广泛用于建筑供能。典型可再生能源太阳能因分布广、获取自由等特点,常与冷热电联供(CCHP)系统耦合用于城市建筑,可进一步缓解能源与环境问题[1-4],实现多能流供能和能量梯级利用,保障用户用能稳定性,提高经济效益。
国内外学者针对耦合系统供能策略展开研究[5-10]。Yang[11]和Dong[12]等人对太阳能耦合CCHP 系统构造仿真建模,得到最优运行方案,为智能电网下可再生能源的高效利用提供参考。Wang 等人[13]提出以二甲醚为原动机燃料的太阳能CCHP 系统生成运行优化方案。荆有印等[14]对太阳能CCHP 系统进行多目标优化分析,发现耦合系统性能优于传统联供系统。金锋等[15]利用k-means 聚类方法优化典型日CCHP 系统出力,得到经济效益最佳的运行策略。任福康等[16]构建耦合太阳能和地热能的CCHP 系统模型,对比分析了以电定热和以热定电运行策略下系统区别。
但已有研究未有效反映太阳能系统出力的波动性,同时忽略了系统容量配置和运行方案间的相互制约关系,故太阳能CCHP 系统供能效果不佳。本文在考虑太阳能系统出力波动性的基础上,使用PVsyst 软件准确估算光伏发电系统出力,构建耦合太阳能的CCHP 系统双层优化模型,通过改进的KKT 算法求解,并以上海某酒店为例验证模型对建筑供能系统节能降耗的推动作用。
1 基于PVsyst 的光伏发电模型构建
PVsyst 软件含有丰富的气象资源库、光伏组件和逆变器数据库和定量分析工具等,常被用于光伏发电系统的建模仿真[17-20]。该软件可综合分析不同影响因素对光伏发电系统发电量的影响,最终求得较为准确的光伏出力。利用PVsyst 软件建立目标酒店光伏发电系统仿真模型,后续进行双层优化方案设计。
1.1 建模过程分析
在使用PVsyst 软件进行光伏发电系统建模仿真时,首先应确认气象数据、光伏组件的倾斜角度及安装方式和型号、逆变器的数量,然后根据软件内置机理过程,最终得到出力。图1 展示了PVsyst软件建模流程。
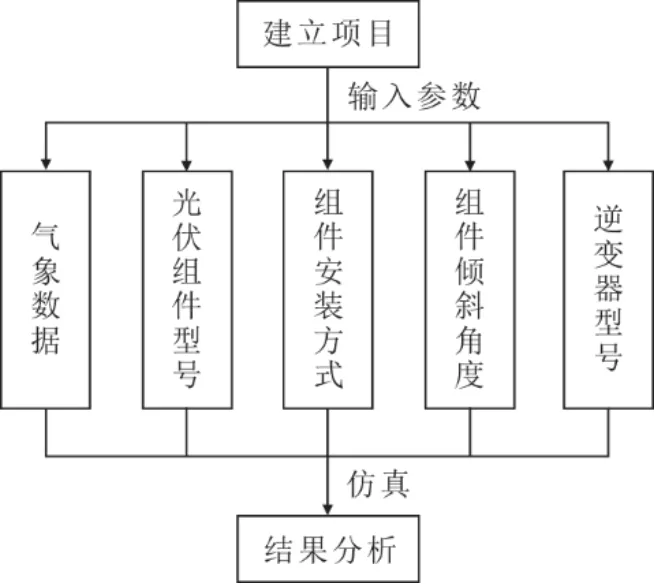
图1 PVsyst 软件建模流程Fig.1 The modeling flowchart of PVsyst software
1.2 参数选取
光伏发电系统的运行原理:太阳能电池利用光生伏特效应将太阳能直接转化为电能,光伏电池板用于接受太阳辐射,产生的光生载流子在半导体作用下分开产生电动势[21-22]。图2 为PVsyst 软件各组件参数选取和设置的主要界面。目前,常见的光伏电池板为单晶硅光伏电池板和多晶硅光伏电池板[23]。单晶硅光伏电池板的转换效率更高,但造价高;相比之下,多晶硅成本低、使用寿命长。本文选择型号为ZYPV-566O25OP 的多晶硅光伏组件,具体参数如图2a 所示。在光伏组件输出能力确定之后,根据光伏阵列容量与逆变器容量比在0.8~1.2 之间的原则,选定光伏逆变器容量。该酒店选择型号为NT6000 的逆变器,具体参数如图2b)所示。目标酒店屋顶光伏系统可利用面积为2 000 m2,光伏系统组件安装方式为固定式(图2c)),组件采用串并联结合的形式(图2d))。
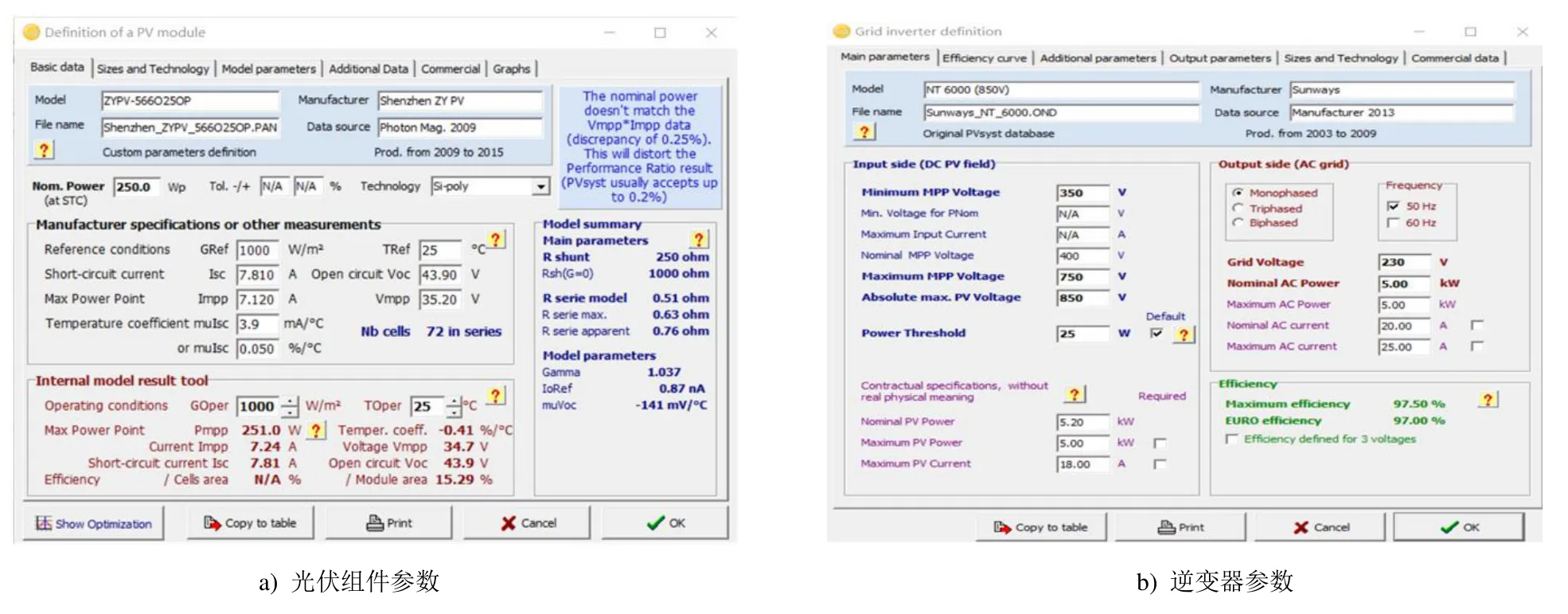
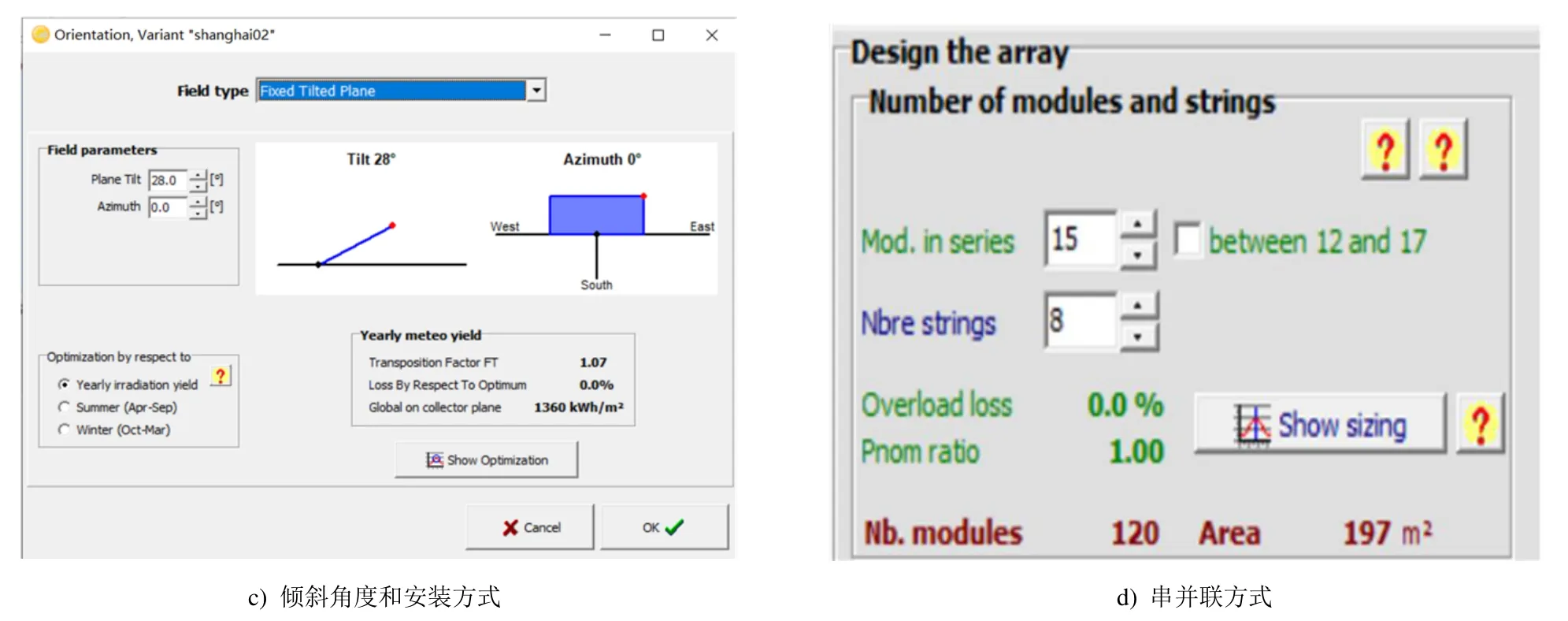
图2 PVsyst 软件参数设置主要界面Fig.2 The display of parameter-design of PVsyst software
1.3 仿真结果分析
在确定光伏系统主要参数的基础上,运行PVsyst 软件获得该酒店光伏发电系统最大理论出力值如图3 所示。由图3 可见,该酒店光伏发电系统年平均发电量达33.2 MW·h,光伏系统发电的综合效率(performance ratio)为73.3%。上海地区的太阳能辐射量呈现夏、秋季较高,春、冬季较少的趋势。其中,7 月份太阳能辐射量最大,发电量达到全年峰值3 361.6 kW·h;1 月份太阳能辐射量最小,发电量为全年最低值2 148.9 kW·h。
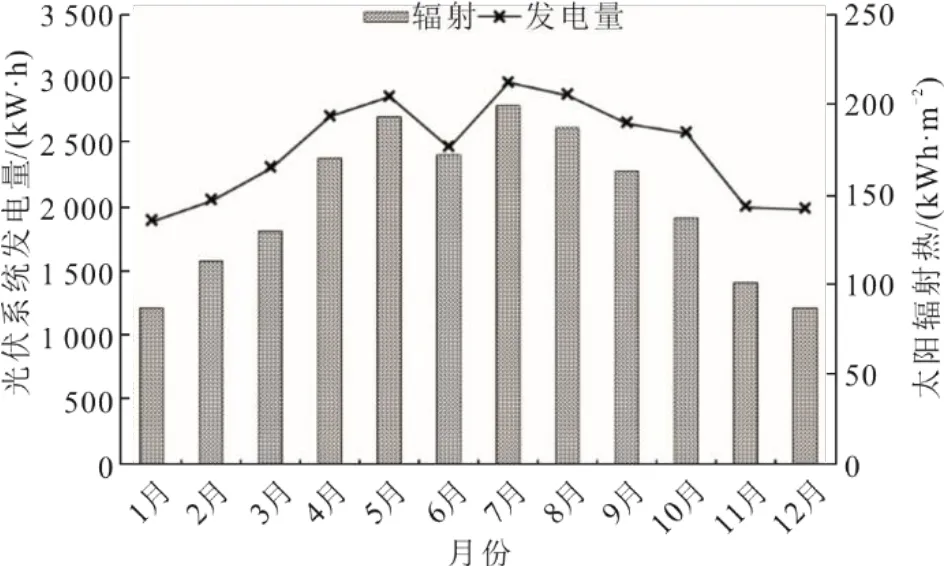
图3 太阳辐射情况和发电量计算结果Fig.3 The calculated solar radiation and electricity output
2 太阳能CCHP 系统双层优化模型构建
2.1 运行流程分析
该太阳能CCHP 系统主要由6 个部分构成,分别是太阳能光伏发电机组、燃气轮机、余热锅炉、补燃锅炉、溴化锂制冷机和电制冷机组。图4 为整个系统的运行流程。首先,燃气轮机燃烧天然气发电的同时,产生的高温余热烟气通过热回收系统提供给溴化锂吸收式制冷机组和余热锅炉等换热设备,分别向用户提供冷量和热量。另外,为确保用户需求得到充分满足,在优先利用余热的前提下,增加补燃锅炉和电制冷机组分别作为辅助的热源和冷源。最后,由于该系统并网运行,如光伏发电和燃气轮机发电无法满足用户的电需求,可通过从公共电网购电来实现供需平衡。太阳能发电系统与CCHP 系统的耦合使用,可有效弥补太阳能的间断性及能流密度低等缺点,也可降低CCHP 系统中非可再生能源的一次消耗量,在适当的配置和运行方案下发挥更大的作用。
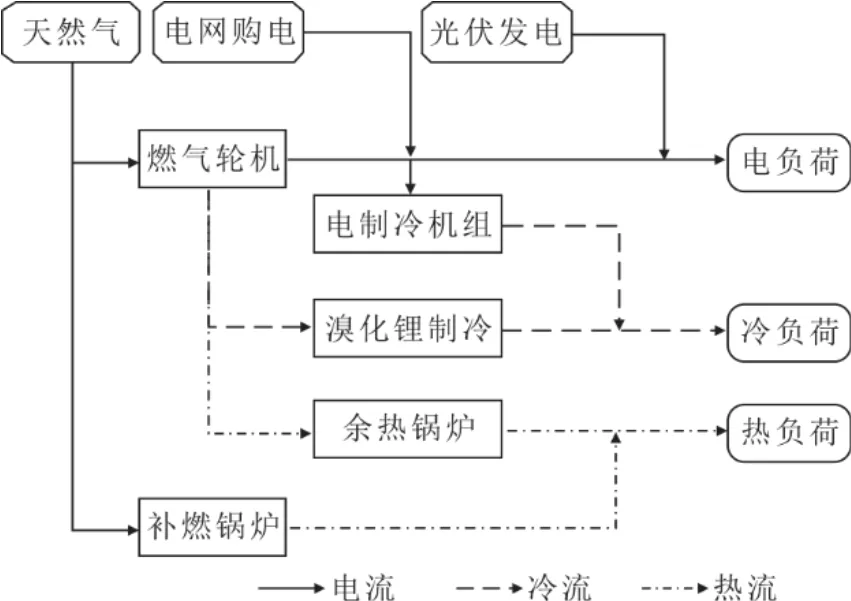
图4 太阳能CCHP 系统运行流程Fig.4 The operational procedure of hybrid solar and CCHP system
2.2 双层优化模型构建
在综合考虑用户侧需求特点和供应侧设备出力特性的基础上,分别构建上层系统配置优化模型和下层系统运行优化模型,运用KKT 条件(Karush-Kuhn-Tucker conditions)将其转换为单层优化模型[24-25]并进行求解,最终得到综合效益最佳的太阳能CCHP 系统配置和运行方案。
2.2.1 上层配置优化模型
上层配置优化模型以系统配置成本最小化为目标函数,以设备容量满足用户侧需求为主要约束条件,具体形式如下。
目标函数为:

式中:Cgt为燃气轮机的单位成本,元/kW;Egt(t)为燃气轮机在t时刻的发电量,kW;Chb为余热锅炉的单位成本,元/kW;Qhb(t)为余热锅炉在t时刻的供热量,kW;Car为吸收式制冷机的单位成本,元/kW;Car(t)为吸收式制冷机在t时刻的供冷量;Ccb为补燃锅炉的单位成本,元/kW;Qcb(t)为补燃锅炉在t时刻的供热量,kW;Cer为电制冷机的单位成本,元/kW;Cer(t)为电制冷机在t时刻的供冷量;Cpv为光伏发电系统的单位成本,元/kW;Epv(t)为光伏发电系统在t时刻的发电量,kW。
主要约束为:
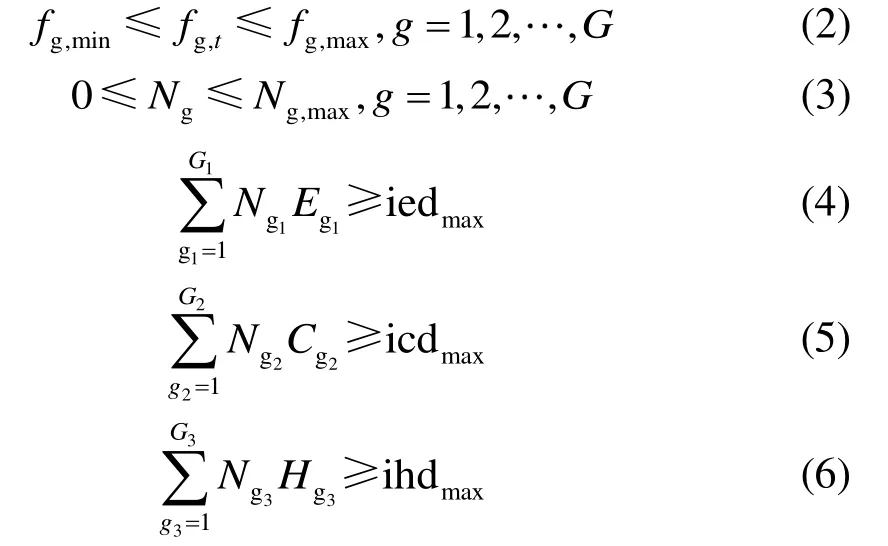
式中:fg,min为设备g 的最小功率,kW;fg,max为设备g 的最大功率,kW;fg,t为设备g 在t时刻的实际输出功率,kW;Ng,max为设备g 的最大数量;Ng,1为供电设备g1的数量;Eg,1为供电设备g1的单位供电量,kW;iedmax为用户的最大电需求,kW;Ng,2为供冷设备g2的数量;Cg,2为供冷设备g2的单位供冷量,kW;icdmax为用户的最大冷需求,kW;Ng,3为供热设备g3的数量;Hg,3为供热设备g3的单位供热量,kW;ihdmax为用户的最大热需求,kW。
2.2.2 下层运行优化模型
下层运行优化模型以系统年度运行成本最小化为目标函数,以能量供需平衡和设备容量限制为主要约束条件,具体形式如下。
目标函数为:
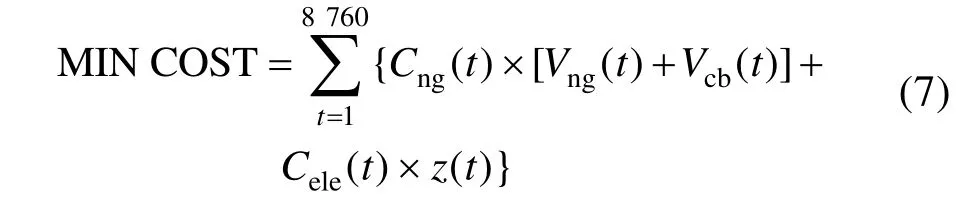
式中:Cng(t)为天然气在t时段的价格,元/m3;Vng(t)为燃气轮机在t时段消耗的天然气量,m3;Vcb(t)为燃气锅炉在t时段消耗的天然气量,m3;Cele(t)为t时段公共电网的电价,元/kW·h;z(t)为t时段系统所需的购电量,kW·h。
主要约束为:
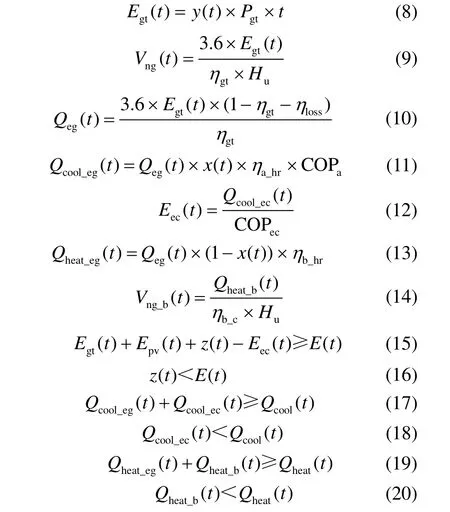
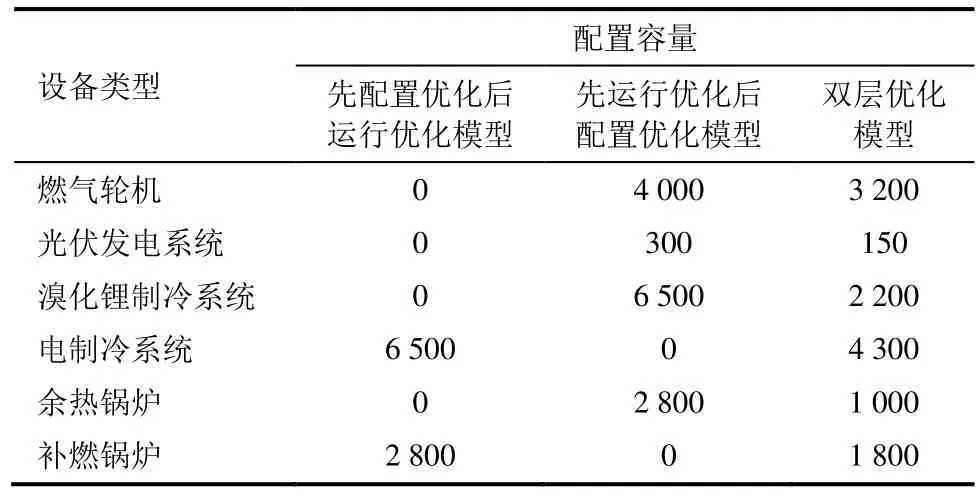
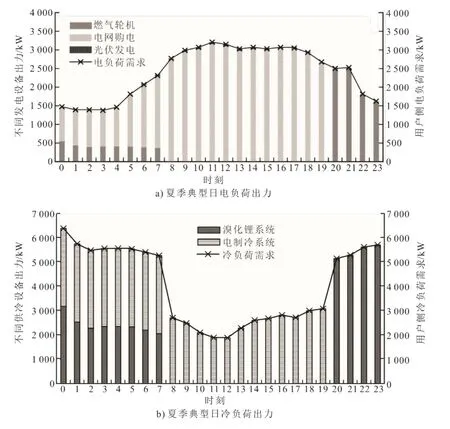
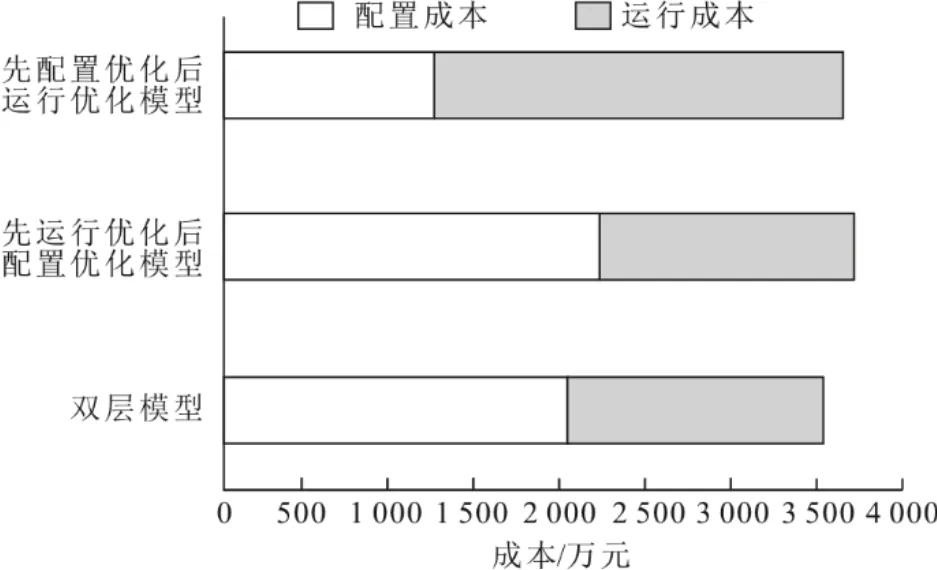
式中:Egt(t)为燃气轮机在t时段的发电量,kW·h;Pgt为燃气轮机的额定功率,kW;y(t)为燃气轮机在t时段的发电出力情况(当y(t)=1 时,燃气轮机满负荷运行,y(t)=0 时,燃气轮机停止运行,0 2.2.3 基于KKT 条件的双层优化模型求解 鉴于构建的双层模型属于混合整数线性规划,且上层与下层模型之间存在交互关系,很难直接进行求解。因此,本文通过构建下层模型的拉格朗日函数,将下层模型转换为上层模型的约束条件,形成新的非线性规划模型,并利用Lingo14.0 软件求解,具体求解流程如图5 所示。 图5 双层优化模型求解流程Fig.5 The solution algorithm of bi-level optimization model 下层优化模型经KKT 转换后得到的拉格朗日函数表达式为: 式中:λ1、λ2、λ3、λ4、λ5、λ6和λ7为等式约束对应的拉格朗日乘子;μ1,max、μ2,max、μ3,max、μ4,max、μ5,max和μ6,max为不等式约束对应的拉格朗日乘子。 上海市地处中国东部沿海地区,界于东经120°52′~122°12′,北纬30°40′~31°53′之间,在民用建筑分类热工设计气候分区中,上海市属于夏热冬冷地区,具备亚热带季风性气候特点,呈现出季风性、海洋性气候特征,冬夏寒暑交替,四季分明。案例酒店坐落于上海市浦东新区,地处上海市东部,建筑面积为53 330 m2,地下3 层,地上29 层,总高度为124 m,绿化率达到50%。该酒店具有客流吞吐量大、入住率高(平均月入住率高达60%)、耗能种类多(包括电负荷、采暖负荷、供冷负荷和生活热水负荷)、耗能量大、供能可靠性要求高等特点。因此,适合采用位于酒店附近具有灵活供能机制的太阳能冷热电联供系统作为其能量源。 在综合考虑系统配置成本和运行成本全局最优的基础上,本文利用Lingo14.0 软件求解双层优化模型,确定该酒店供能系统的最佳设备组合和容量配置、以及逐时的设备出力策略和总成本。为了对比,本文分别构建了“先配置优化后运行优化”模型和“先运行优化后配置优化”模型,并对其进行求解。“先配置优化后运行优化”模型是首先构建以系统配置成本最小化为目标函数,满足用户的能源需求和设备功率限制等约束条件的供能系统配置优化模型;然后,将求解得到的设备功率作为主要参数输入到系统运行优化模型的设备出力约束中,结合用户的逐时能源需求,最终优化生成系统运行方案。与“先配置优化后运行优化”模型的构建程序相反,“先运行优化后配置优化”模型是首先构建以系统运行成本最小化为目标函数,考虑能源供需平衡和设备最大输出功率的系统运行优化模型(其设备最大输出功率是由用户的逐时最大能源需求和设备性能共同决定的);然后,将供能设备出力的求解结果,代入到配置优化模型中,确定适合的供能设备,最终生成系统最优配置方案。 3.2.1 3 个模型的配置对比 表1 给出了3 个模型的配置结果由于燃气轮机作为CCHP 系统的主要动力装置,其单位配置成本较高。但是,在运行阶段,燃气轮机发电的同时,产生的余热烟气可供余热锅炉和溴化锂制冷机组使用。因此由表1 可见:“先配置优化后运行优化”模型不配置燃气轮机、余热锅炉和溴化锂制冷机组,光伏发电系统也因高配置成本被弃用;相反,由于“先运行优化后配置优化”模型仅考虑运行成本,供能系统充分发挥了燃气轮机的能源梯级利用优势,燃气轮机的配置容量达到最大额定功率4 000 kW,余热锅炉和溴化锂制冷系统的配置容量分别为2 800 kW 和6 500 kW,光伏发电系统的配置容量同样达到最大,即300 kW。双层优化模型的CCHP 系统在以燃气轮机(3 200 kW),余热锅炉(1 000 kW)和溴化锂制冷系统(2 200 kW)为首选供电、供热和供冷设备的基础上,增加了补燃锅炉(1 800 kW)、电制冷机(4 300 kW)和光伏发电系统(150 kW)作为辅助供热、供冷和供电方式,极大地增强了系统供能的灵活性和鲁棒性。 表1 3 类优化模型的系统配置方案对比 单位:kWTab.1 The comparison of system configuration among three optimization models 3.2.2 双层优化模型的供电和供冷设备出力 耦合系统内部的一些关键参数和运行机制均对设备出力产生影响。本文选择夏季典型日作为示例,研究不同时段供能方案的变化。图6 为求解双层优化模型得到的夏季典型日供电和供冷设备的出力情况。 图6 夏季典型日系统供能方案示意Fig.6 Schematic diagram of energy supply scheme in typical summer day 由图6 可见,峰、平、谷电价政策的实施,对不同时期设备出力产生了明显影响。夏季典型日(图6a))用户侧的电需求高峰为8:00—19:00,此时,用户侧电需求由光伏发电系统和电网购电协同供应,其中在用电需求最大的时刻11:00 时,光伏系统发电量和电网购电量分别为46.99 kW 和3 160.67 kW。在电价峰期20:00—23:00,用户侧的电需求全部由燃气轮机来满足,其中21:00 时燃气轮机发电量最大,为2 525.67 kW。另外,为了充分发挥CCHP 系统的能源梯级利用优势,在用户侧电需求较小的电价谷时段0:00—7:00,为了节约系统制冷成本,燃气轮机仍处于运行状态。 由阶梯电价和运行机制给供冷设备出力带来的影响可见,在用户侧冷负荷高峰期0:00—7:00,供能系统采用电制冷系统和溴化锂系统联合运行的方式以保证冷量的正常供应。由于该时段为电价的低谷阶段,电制冷系统作为主要冷源,处于满负荷运行状态(3 200 kW)。其中,在冷负荷最低时刻7:00,溴化锂的供冷量仅为2 066 kW。在8:00—19:00,用户侧的冷需求相对较低,此时,用户侧的冷需求全部由电制冷系统满足,其中在冷需求量最高时刻16:00,电制冷系统的出力为2 821 kW。在电价最高的20:00—23:00 时段,用户侧的冷需求较高,该时段内溴化锂制冷系统作为主要冷源,电制冷系统不运行,在冷负荷需求最高时刻23:00,溴化锂系统的制冷量为5 699.94 kW。 3.2.3 3 个模型的成本对比 由于3 个优化模型的设备容量配置和运行方案均不相同,因此模型的总成本存在一定的差异。图7 为求解3 个优化模型得到的该酒店供能系统配置和运行成本。由图7 可见:由于“先配置优化后运行优化”模型在满足用户需求的前提下仅考虑配置成本最低,因此配置成本最低,为1 248.05 万元;“先运行优化后配置优化”模型和双层优化模型的配置成本分别为2 216.00 万元和2 015.71 万元;“先运行优化后配置优化”模型的运行成本最低,为1 487.38 万元;“先配置优化后运行优化”模型和双层优化模型的运行成本分别为2 391.78 万元和1 506.68 万元。双层模型作为耦合系统容量配置和运行优化的综合模型,虽未实现单一目标函数的最优,但是,其配置和运行的总成本最小,为3 522.39 万元;另外两个模型分别为3 703.38 和3 639.83 万元。该结论充分证明了双层优化模型能较好地实现系统配置和运行之间的联动,达到全局最优,具有更好的应用前景。 图7 3 个模型成本对比分析Fig.7 The comparison of total system cost among three models 1)本文针对建筑供能系统配置和运行过程割裂的问题,提出了耦合配置和运行优化的太阳能CCHP 系统双层优化模型。考虑到光伏发电系统出力的波动性,在运用PVsyst 软件准确预测光伏出力的基础上,创新性地实现了光伏出力预测和供能系统优化的有效结合,最终得到了太阳能CCHP 系统的最佳配置和运行方案。 2)与传统的“先配置优化后运行优化”和“先运行优化后配置优化”单层优化模型对比,双层优化模型可显著提高系统供能的灵活性和可靠性,有效避免可再生能源出力波动导致的能源供需失衡,以及获取更大的经济效益。 3)后续研究可采用鲁棒性更强的双层优化模型求解算法,以便更好地反映上层模型和下层模型的交互关系。另外,设备仿真模型与双层优化模型的联合使用,有助于准确计算系统各设备的出力,从而得到适应性更强的供能方案。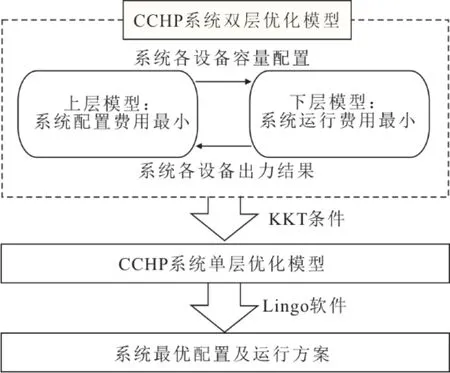
3 算例分析
3.1 案例介绍
3.2 结果分析
4 结论
