细长剪力墙结构的抗震性能研究
2022-06-09司海玉
司海玉
(东华工程科技股份有限公司,安徽 合肥 230041)
1 工程概况
取某采用细长剪力墙结构的已建高层住宅建筑为研究对象。该工程建设于安徽合肥,地上24层,地下1层。本工程抗震设防基本烈度为7度0.10g,抗震设防类别为丙类,设计地震分组为第一组,建筑物场地类别为II类,场地特征周期为 0.35s;基本风压:W0=0.60kN/m2(承载力设计时按基本风压的1.1倍采用),地面粗糙度类别:B类;基本雪压:0.60kN/m2。
2 细长剪力墙的弹性分析
2.1 SATWE计算结果分析
采用两种不同力学模型的结构分析软件PKPM进行小震作用下结构的内力和变形分析,计算结果如下:
① 周 期 T1=1.5511s(平 动 系 数 为0.99)、T2=1.4981s(平动系数为 0.98)、T1=1.2406s(平动系数为 0.03),周期比为0.80<0.9;
②考虑偶然偏心的地震作用,本工程X向最大层间位移比为1.14(26层),Y向最大层间位移比为1.14(16层),两者均满足《高规》[2]3.4.5条的要求;
③查看SATWE计算结果位移输出文件,在地震作用下,X方向的最大层间位移角为1/2974,所在层号为第13层,Y方向的最大层间位移角为1/3128,所在层号为第18层,两者均满足《高规》对结构的水平位移限值和舒适度的要求;
④该结构不存在侧向刚度不规则、竖向抗侧力构件不连续和楼层承载力突变中的任何一个,故判断本工程无薄弱层;
⑤本工程剪力墙抗震等级为三级,按照规范,三级要求轴压比不能超过0.6。 对 第 十 层(标 准 层 ,墙 厚 为160mm)的剪力墙轴压比分布在0.27~0.40,且85%分布在0.27~0.34的范围内,可见各墙肢轴压比比较接近,每一道剪力墙都能够充分发挥其作用。
综上可知,该结构在多遇地震下包括承载力验算和弹性变形计算在内的弹性计算结果均能满足《抗规》[3]、《高规》的要求。
2.2 弹性动力时程分析
2.2.1 地震波的选择
此时进行弹性动力时程分析的主要目的是筛选出适合的地震波,从而为下一步的罕遇地震弹塑性动力时程分析做基础工作。高层建筑结构进行动力时程分析采用的地震波有人工模拟地震波、典型的强震记录和场地的实际地震记录[4]。地震波选取步骤按文献[5]。
查SATWE软件输出的“周期、振型、地震力”文本文件(WZQ.OUT),得本工程X向基底剪力为3509.78kN,Y向基底剪力为3839.42kN。
该工程场地类别为II类场地土,其对应的特征周期T=0.35s,在计算罕遇地震作用时,特征周期应增加0.05s。根据这两个条件,选择两条人工波、六条天然波进行试算。该八条地震波的波谱与规范谱的对比图如图1(a)所示。根据该要求筛选出两条天然波TH4TG040、TAF-2以及一条人工波RH4TG040。该三条波的波谱与规范谱的对比图如1(b)所示。各地震波的相关参数如表1所示,加速度时程图分别如图2~图4所示。
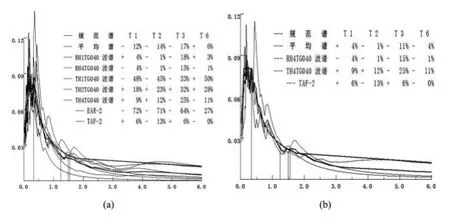
图1 规范谱与地震波谱对比图

地震波参数 表1
图2 地震波加速度时程图(RH4TG040)
图3 地震波加速度时程图(TH4TG040)
图4 地震波加速度时程图(TAF-2)
经计算得这三条波及反应谱法在X向、Y向所计算的基底剪力和基底弯矩如表2所示。
根据以上计算结果可知,所选择的地震波的时程分析结果满足《高规》
4.3.5 条2款的要求。
2.2.2 弹性动力时程分析结果
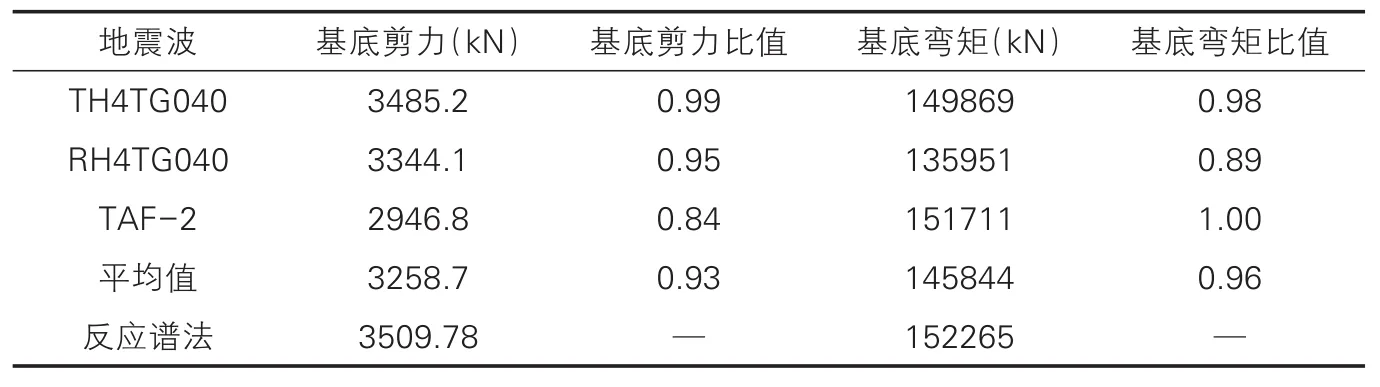
①三条地震波计算的结构X、Y向最大层间位移及位移角如图5、图6所示。
从表2和图5、图6可知,振型分解反应谱的计算结果均大于采用弹性动力时程分析的计算结果,所以振型分解法的计算结果满足要求。
TH4TG040、RH4TG040、TAF-2及平均基底剪力在X、Y的计算结果 表2

图5 结构X向最大层间位移及位移角曲线
图6 结构Y向最大层间位移及位移角曲线
②三条地震波的最大层间位移角如表3所示。

三条地震波的最大层间位移角 表3
分析以上数据可知,该结构平面布置和刚度分布都比较规则。X向结构的最大层间位移比主要出现在第19层,Y结构的最大层间位移比主要出现在第24层,计算结果均小于《高规》规定的1/1000;在X向、Y向的位移比分别为1.18、1.17;其周期比为 0.73,这说明结构的位移及抗扭转效应都比较好。
3 细长剪力墙的静力弹塑性分析
本工程采用PKPM-PUSH进行分析。
3.1 X向弹塑性静力推覆分析
①罕遇地震下结构的需求曲线、能力曲线及抗倒塌验算结果如图7所示。

图7 X向罕遇地震下结构的需求曲线、能力曲线及抗倒塌验算结果
图7中,加速度需求谱曲线与周期-最大层间位移角曲线的交点即为性能点。该工程的需求层间位移角为1/599,小于《高规》规定的限值1/120,满足在罕遇地震作用下规范规定的要求,这表明该结构具有足够大的强度和刚度,在罕遇地震下不会发生倒塌破坏。
②与性能点相对应的总加载步号为29,所对应的结构主方向位移、主方向剪应变曲线和主方向位移角如图8所示。

图8 第29加载步所对应的结构主方向位移、主方向剪应变曲线和主方向位移角
根据上述结果,本工程罕遇地震作用下,层间位移和层高的关系基本为线性,位移角和剪应变在结构高度中部以下呈线性递增的状态,而在结构中部出现拐点,中部以上则呈现递减状态。X主方向最大层间位移为98.50mm,出现在顶层;最大层间位移角为1/599,所对应的层号为第11层。
③第29加载步所对应的结构杆端塑性状态如图9所示。

图9 第29加载步所对应的结构杆端塑性状态
通过图9可以发现,剪力墙、梁端等部位都出现较多的塑性铰,此结果说明结构变形已经处于弹塑性阶段(黄色表示曾经出现的塑性铰,红色表示当前加载步的塑性铰);较大部分的塑性铰出现在结构的底部,说明结构底部为薄弱部位,在设计时应特别考虑。
④在性能点处,第11层的位移-荷载、位移角-荷载、剪应变-荷载曲线如图10所示。

图10 性能点处,第11层的位移-荷载、位移角-荷载、剪应变-荷载曲线
由于篇幅所限,本文未列出Y向弹塑性静力(动力)推覆分析结果,其结果与X向的类似。

图11 X向最大楼层位移、最大层间位移角及最大有害位移曲线
综上,在罕遇地震作用下,该采用细长剪力墙结构的高层住宅建筑在各楼层刚度分布比较均匀,没有出现较为明显的薄弱层;该结构体系的变形形态为弯剪型,过渡层以上剪力起主导作用,过渡层以下则由弯矩控制。因此建议在该结构在过渡层以上部分重点考虑抗剪,过渡层以下部分重点考虑抗弯,而在过渡层部位则需要同时考虑抗弯抗剪加强。
4 细长剪力墙的弹塑性动力时程分析
4.1 X向弹塑性动力时程分析
在其X主方向用PKPM-EPDA软件对该结构进行弹塑性动力分析,结果如下:
①在罕遇地震作用下,三条地震波在X主方向产生的最大楼层位移、最大层间位移角及最大有害位移曲线如图11所示;
②在罕遇地震作用下,三条地震波产生的结构塑性分布如图12所示。
图12 X向最大层间位移角时刻的结构裂缝和塑性铰分布图
4.2 罕遇地震作用下的变形验算结果
本工程在三条地震波的分别作用下,结构最大层间及有害位移角的数值及所对应的层号如表4所示。
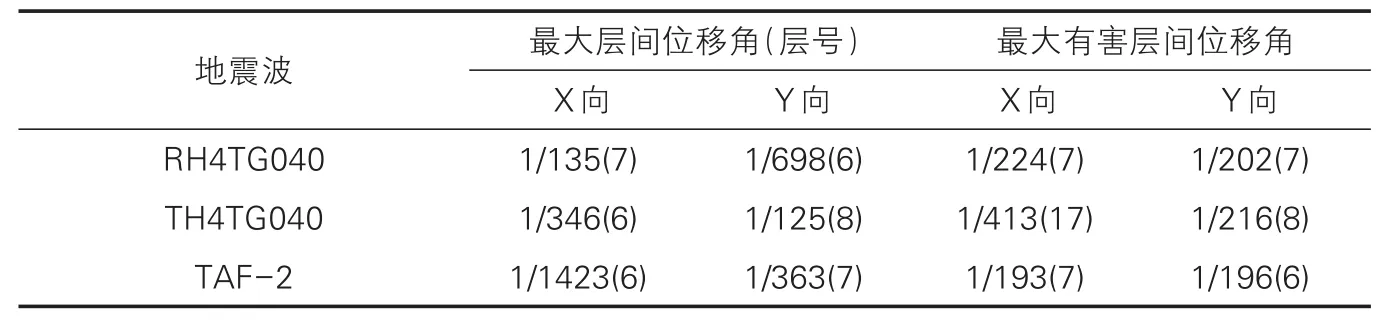
结构最大层间及有害层间位移角的计算结果 表4
5 结论
本文通过对某24层采用细长剪力墙结构体系的高层住宅进行弹性分析、弹性动力时程分析、静力弹塑性分析和弹塑性动力时程分析,可以得到以下结论:
①通过对结构的弹性分析可知,该结构在多遇地震下包括承载力验算和弹性变形计算在内的弹性计算结果均能满足《抗规》《高规》的要求,即“第一阶段设计”完成,该结构在水平力作用下的变形曲线呈弯剪型;
②通过对结构的弹塑性静力分析可知,该工程在罕遇地震作用下的需求层间位移角为小于规范限值1/120,表明该结构强度和刚度均符合规范要求,即在罕遇地震下不会发生倒塌破坏;
③通过对结构的弹塑性动力时程分析可知,结构构件变形性能及整体性能的结果表明,结构能够满足“大震不倒”;结构的层间位移角及弹塑性位移均能满足《抗规》《高规》等的限值要求,且有一定的冗余度。
