完全剪力连接叠合板组合梁静力试验研究

袁西贵

完全剪力连接叠合板组合梁静力试验研究

袁西贵

（成都职业技术学院城建学院，四川 成都 610218）

通过完全剪力连接叠合板组合梁静力试验结果，对比分析了基于平截面假定并考虑滑移效应影响得到的现浇板组合梁的承载力计算公式，结果表明，两者的力学性能没有明显的差别，均可采用现浇板组合梁承载力计算公式。

完全剪力连接；叠合板；剪力连接程度

钢-混凝土组合梁能充分利用材料的受力特性，具有抗震性能好、刚度大、施工方便、造价低等优点，在欧美、日本等得到了广泛应用[1]。在我国目前也备受工程界关注，多用于一些承受重复荷载作用的结构构件中，如桥梁工程、厂房吊车梁等。

随着工厂化、工业化装配式技术的推广，作为半装配式的叠合板组合梁在房屋建筑工程中运用越来越受欢迎。因其具有不中断交通、便于组织立体作业、现场湿作业少、施工速度快等优势更是在桥梁工程中具有广泛应用前景[1-2]。

目前有关叠合板组合梁的研究甚少，已有研究成果大多针对现浇板组合梁。为充分发挥它们在山区、丘陵地区中小跨径桥梁建设及相关工程中的作用，亟需对其进行包括疲劳性能在内的受力性能试验研究，以便为完善我国相关设计规程、规范提供参考。本试验主要是通过静力试验了解完全剪力连接叠合板组合梁的力学性能，并为后续疲劳性能试验研究打下基础。

1 试件设计

1.1 材料性能

钢筋采用HPB300；栓钉型号16 mm×65 mm，所用材料为16Mn钢经冷拔、锻造而成，取栓钉极限抗拉强度su=450 MPa；钢梁采用Q235B，翼缘屈服强度f、腹板屈服强度w及其极限强度u按材性试验如下取值：f=286 MPa，w=350 MPa，u=450 MPa。混凝土材性试验结果见表1。

表1 梁FSCB-0混凝土材性试验结果 MPa

预制层 现浇叠合层 fcufcEcfcufcEc 50.940.73269248.438.732240

1.2 组件设计

试件采用跨度为4 500 mm简支梁。焊接钢梁上下翼缘宽分别为90、200 mm，钢梁总高220 mm。腹板厚度实测值为5.8 mm，上翼缘厚为10 mm，下翼缘实测厚9.9 mm。

混凝土翼缘板预制板厚35 mm，上下边缘宽分别取700、740 mm，板底留10 mm缝宽，板跨方向取425 mm；现浇层厚为45 mm，整个叠合板板厚为80 mm。梁每侧各6块预制板，每块板内配106下部纵向受力筋，66板横向分布筋，间距均为75 mm。预制板在钢梁上支承长为20 mm，板跨方向长425 mm，梁翼缘总宽900 mm，其中槽口下部净宽50 mm。预制板截面参数详见图1。

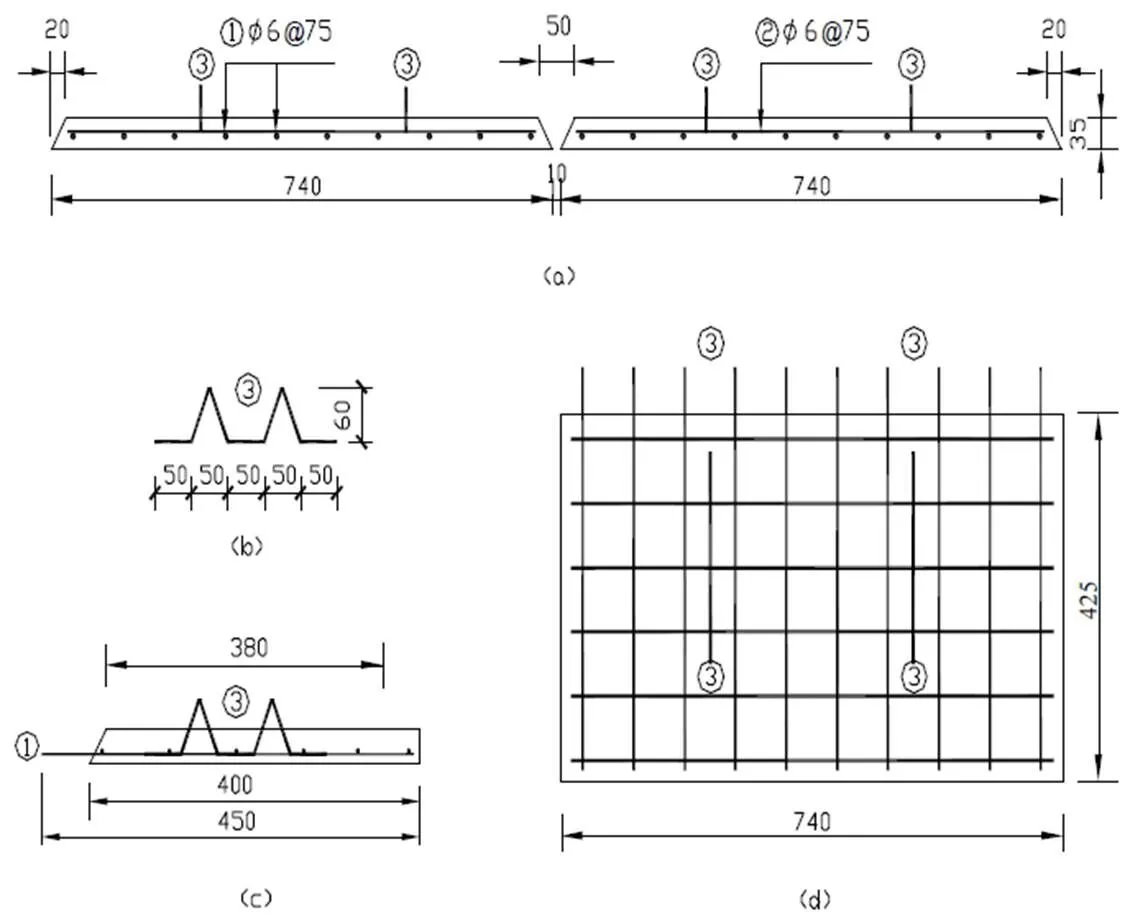
图1 预制板截面及配筋详图

预制混凝土板内设结合钢筋穿过交界面[3]，构造详见图1(b)、(c)。预制板及现浇板混凝土强度均取C40。组合梁FSCB-0截面配筋详见图2。

图2 叠合板组合梁FSCB-0配筋详图

试件按剪力连接件均匀布置的塑性设计法设计，单个栓钉抗剪承载力V=63 347 N。按照完全剪力连接组合梁设计时，半个剪跨区段所需栓钉总个数f=20.053。

1.3 组合梁模型的设计

取一个剪弯段栓钉数为21(实际剪力连接程度为1.047)，栓钉沿钢梁上翼缘均匀对称单列布置。为防组合梁发生掀起等次生破坏，在纯弯区段也布置了4个栓钉。全梁跨共46个栓钉。组合梁FSCB-0的栓钉布置详见图3所示。

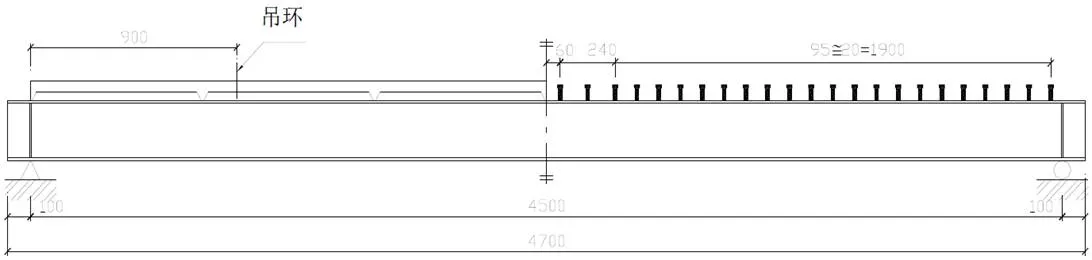
图3 梁FSCB-0栓钉布置

2 现浇板组合梁承载力计算

2.1 现浇板组合梁屈服弯矩的计算

钢板弹性模量E=2.06×105，钢板与混凝土弹性模量(E)之比α=6.372 7。不计混凝土徐变，组合梁等效钢截面宽度1见表2[4-6]。

表2 试验梁的混凝土翼板换算宽度取值

项次fc/MPaαEb1/mm 同条件现浇板39.1226.3727141.23

2.1.1 不考虑滑移效应时组合截面弹性屈服弯矩

本次试验梁同条件现浇板组合截面几何参数及屈服(极限)弯矩计算如表3。

表3 不考虑滑移效应影响组合梁截面计算抗力

中和轴高度X/mm屈服弯矩Mys/(kN·m)屈服弯矩Myc/(kN·m) 228.84193.81424.6

表中为组合梁换算截面中和轴至钢梁下翼缘底边的距离；M为由钢梁下翼缘计算而得组合截面屈服弯矩；M由混凝土翼缘板边缘应力极值计算得组合截面弹性极限弯。

2.1.2 考虑滑移效应时组合截面屈服弯矩

考虑组合梁滑移效应后同条件现浇板组合梁屈服荷载及屈服弯矩如表4。

表4 考虑滑移效应后试验梁同条件现浇板截面计算抗力

项次ζ屈服弯矩My/(kN·m)屈服荷载Py/kN 取值0.9518184.468184.468

注：为考虑滑移效应后弹性弯矩折减系数。

2.2 现浇板组合梁极限弯矩

不计混凝土抗拉，塑性设计时同条件现浇板组合梁混凝土受压区高度p及静力极限承载力u见表5。

表5 试验梁同条件现浇板静力计算极限承载力Mu

项次Xp/mmMu/MPa极限荷载Py/kN 同条件现浇板36.08266.63266.63

组合梁屈服弯矩以及极限弯矩汇总见表6。

表6 现浇板组合梁屈服弯矩以及极限弯矩汇总表 kN·m

项次栓钉数剪力连接度γ不计滑移屈服弯矩考虑滑移屈服弯矩极限弯矩 同条件现浇板211.05193.81184.468266.63

3 试验装置和加载方案

3.1 加力点的确定

试验采用跨中两点对称加载。组合梁静力试验加载方案见图4。

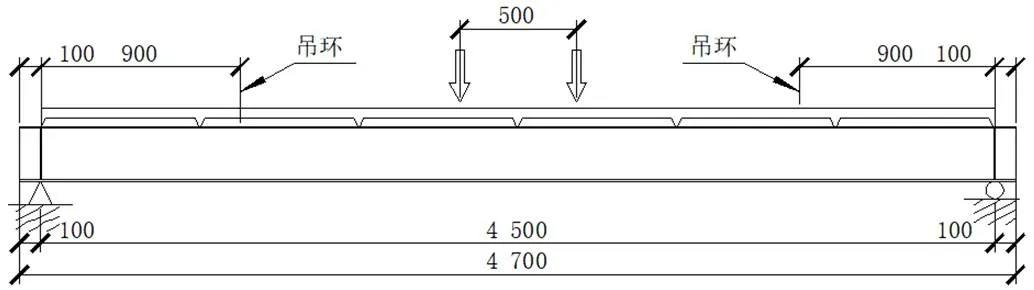
图4 组合梁加载方案

3.2 加载设备

静力试验由1台500 kN的液压脉动疲劳试验机所控制的油压千斤顶分配梁加载。试验机的最大动、静负荷均为500 kN，荷载大小通过与千斤顶相连的测力传感器测量，千斤顶施加的荷载由一分配梁传递到通过坐浆固定于组合梁上表面的2个垫梁上。加载装置如图5。

图5 试验加载装置

3.3 测试装置

数据采集设备包括：用于量测动、静荷载值的测力传感器，用于量测界面滑移、跨中位移等数据的位移传感器；应变仪及配套的数据采集设备和相应软件。

3.4 测试内容及测点布置

(1)量测内容

量测设备通道共16个。其中测力及跨中挠度的通道各1个，跨中截面钢梁及混凝土上分别布置4～5个应变测点；在梁半跨内布置5个量测混凝土与钢梁交界面相对滑移的测点；裂缝宽度用刻度片观测记录。

(2)测点布置

图6给出了试验梁的测点及仪表布置详图。图中C表示在混凝土翼缘板上粘贴的电阻应变片，S表示在钢梁上粘贴的电阻应变片(这里表示离钢梁下翼缘距离)；D表示量测混凝土翼缘板与钢梁间相对滑移以及量测组合梁跨中位移的动态位移传感器。

图6 测点布置图

为了量测组合梁跨中截面的应变分布，在混凝土翼缘板上、下表面及侧面布置5个电阻应变片，钢梁的翼缘下缘及腹板布置4个电阻应变片。此外，为量测相对滑移，在混凝土翼板与钢梁交界面处布置位移传感器；为量测跨中挠度，试验梁的跨中装有大量程位移计(200 mm)。

4 试验现象

加载至180 kN时，纯弯区段预制板交接槽口下表面出现一条很细的短裂缝，直至极限荷载约276 kN时该裂缝宽度也未超过0.4 mm(对应的跨中位移为78 mm)，破坏后混凝土板裂缝如图7所示。

图7 静力破坏后混凝土板裂缝示意图

图8 梁FSCB-0力-滑移曲线

图9 梁FSCB-0破坏形态图

5 实验结果与分析

5.1 试验主要现象分析

加载初期的声响主要是钢梁焊缝处初始残余应力在受力后发生了重分布以及支座和分配梁等传力、加力设备在相互接触处受力压紧所致。

破坏时栓钉无一被剪断，说明完全剪力连接组合梁栓钉抗剪强度足够。原因有三：一是静力试验中钢梁不可能全截面屈服，按塑性分析法设计的栓钉抗剪能力是足够的；二是混凝土板与钢梁上翼缘间的自然黏接非常明显，这有助于栓钉抗剪；三是对称加载作用点下方形成了较为集中的摩擦力，起到了栓钉的抗剪作用。

试验中，裂缝不断加长变宽，但始终短小，主要因为组合梁屈服前混凝土板下缘要么受压，要么受拉，受拉时，直到破坏其拉应变也不大，从而推迟了混凝土的开裂并减少了裂缝宽度。

整个加载过程中，钢梁没有拉裂，后期一直处于屈服平台阶段，组合梁表现出良好的延性，这有利于结构抗震。组合梁直到试件失效也没出现可见的滑移，自然黏接仍未完全破坏。

此外，纯弯区段叠合板间交接面槽口处，即使挠跨比已达1∶60时，混凝土裂缝开展宽度也很小。虽然薄弱面首先出现在预制板间交接面槽口处；但该处裂缝和预制板板内裂缝几乎是同时出现的，说明槽口截面混凝土抗拉强度和预制板内混凝土抗拉强度是相当的。可以预见，即使是承受疲劳荷载，采取恰当的工艺处理叠合面，叠合板组合梁质量也是可以保证的。此外，由于试件设计是按照规范构造要求进行的，破坏时也未发生更为脆性的纵向劈裂破坏。

此外，叠合板组合梁屈服荷载及极限荷载实测值与按现浇混凝土翼缘板计算所得结果一致。实测值所得屈服荷载和极限荷载比理论计算分别提高了5.3%和3.3%。结果略有增大，一是因为计算中未考虑交界面摩擦影响；二是因为材性试验结果与构件本身材性不同。同时理论计算和简化偏于安全。梁FSCB-0静力试验所得力-跨中位移关系如图10所示。

图10 梁FSCB-0力－跨中位移曲线

5.2 试验成果

试验梁截面应变分布如图11～图14所示。

图11 梁FSCB-0截面应变

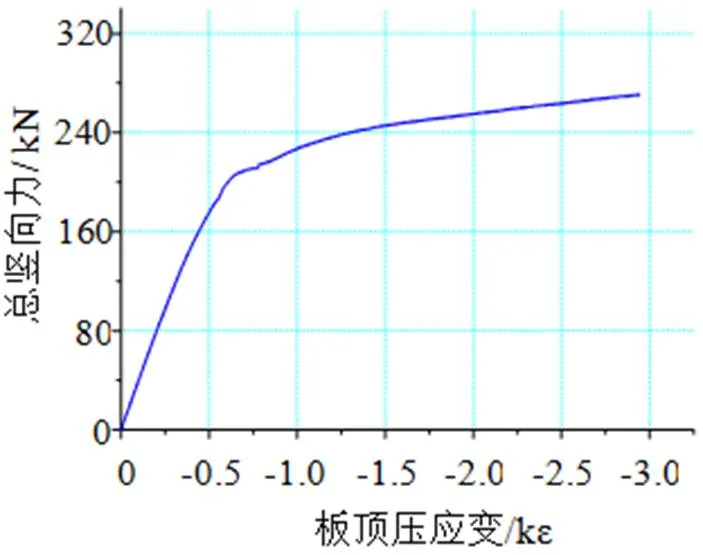
图12 梁FSCB-0混凝土顶面压应变曲线

图13 梁FSCB-0钢梁底面最大拉应变曲线

图14 梁FSCB-0混凝土板底拉应变曲线

由图可见，叠合板组合梁表现了很好的塑性，在屈服前，栓钉连接的组合板与钢梁间的滑移几乎可以忽略不计，叠合板组合梁刚度很大，位移变化相当缓慢，屈服时叠合板组合梁的位移和屈服弯矩不低于按现浇板组合梁计算结果，如表7所示。屈服之后，组合梁表现出很好的延性，极限承载力也较高，安全储备较大，屈服荷载与极限荷载之比约为0.74，叠合板组合梁的这些力学性能十分利于在工程中的应用和推广。

表7 组合梁承载力对比结果 kN

项次屈服荷载极限荷载备注 不计滑移计滑移 现浇板193.81184.468266.63计算值 叠合板204276实测值

6 结论

基于平截面假定并考虑现浇板与钢梁间相对滑移影响得到的完全剪力连接现浇板组合梁承载力计算公式，可直接用于计算完全剪力连接叠合板组合梁。完全剪力连接叠合板组合梁在试验中表现出来的裂缝开展、相对滑移、位移特征、屈服弯矩及极限承载力等力学性能与现浇板组合梁高度一致。

[1] 李建军. 钢-混凝土组合梁疲劳性能的试验研究[D]. 北京: 清华大学, 2002.

[2] 聂建国, 余志武. 钢-混凝土组合梁在我国的研究及应用[J]. 土木工程学报, 1999, 32(2): 3-8

[3] YB 9238—92. 钢-混凝土组合楼盖结构设计与施工规程: [S]. 北京: 冶金工业出版社, 1992.

[4] 聂建国, 沈聚敏, 袁彦声, 等. 钢-混凝土组合梁连接件实际承载力的研究[J]. 建筑结构学报, 1996, 17(2): 21-25.

[5] 聂建国, 刘明等, 叶列平. 钢-混凝土组合结构[M]. 北京:中国建筑工业出版社, 2005.

[6] GB 17—2017. 钢结构设计规程[S]. 北京: 中国建筑工业出版社, 2017.

Static Test Study of Complete Shear Connection Composite Beam with Laminated Slabs

YUAN Xi-gui

（School of Urban Construction, Chengdu Polytechnic College, Chengdu 610218, China）

In this paper, in view of the slip effect, the bearing capacity of composite beam with cast-in-site slabs based on plane cross section assumption is compared by the static test of complete shear connection composite beams with laminated slabs.The results show that there is no significant difference between them. Both can use the same bearing capacity calculation formula.

complete shear connection; laminated plate; shear connection degree

10.15916/j.issn1674-3261.2022.02.011

TU398；TU997

A

1674-3261(2022)02-0122-05

2021-05-26

四川省教育厅2017年度科研计划自然科学类重点项目(17ZA0140)

袁西贵(1971-)，男，四川遂宁人，高级工程师，硕士。

责任编辑：孙 林