基于kd-MDD的时序图紧凑表示

李凤英 申会强 董荣胜

(广西可信软件重点实验室(桂林电子科技大学) 广西桂林 541004)

随着移动互联网、物联网等技术的发展，众多新应用以前所未有的方式和速度产生并积累了海量数据[1].在大数据分析的过程中，图作为一种有效描述大数据的数据结构，扮演着越来越重要的角色[2-4].时序图是将时间维度信息添加到图中的一种多维图，包含了图的演化过程，能够为通信网络、社交网络等数据进行建模，例如当用户添加或删除在线社交网络中的朋友时友谊关系的演变、发布新的科研论文时引文网络的动态性、移动设备更换基站时随时间变化的连接，或在网络图中出现或消失的链接的变更等.时序图包含图的演变过程，不仅可以获取顶点之间的连通性的当前状态，还可以获取其历史状态，可以在不同时间点为诸如通信网络和社交网络等应用程序提供信息.如何有效、紧凑地表示包含数亿个顶点和边的时序图数据，已成为相关领域的研究热点[5-7].

本文在kd-tree的基础上，引入多值决策图(multi-valued decision diagram, MDD)技术，对时序图的紧凑表示与管理进行研究,主要贡献有3个方面：

1) 研究了MDD与时序图之间的关系，设计了一种更加紧凑的时序图表示方法——kd-MDD.在kd-MDD的构建过程中隐式地合并了kd-tree中的同构子树，消除冗余节点，使得多维图数据的存储结构更加紧凑.

2) 实现了时序图的动态管理.研究时序图的查询及编辑操作与MDD逻辑运算之间的关系，给出了kd-MDD表示下时序图的增加/删除边、增加/删除顶点等编辑操作的一系列过程，解决了kd-tree不适用于表示动态图的问题.

3) 在真实的时序图数据集上进行实验，结果表明本文给出的kd-MDD方法表示时序图具有适用性和高效性，为时序图的紧凑表示和高效处理提供了新的方法和技术.

1 相关工作

随着网络技术的飞速发展，数据爆炸式地增长.图作为描述数据的一种有效数据结构，大规模图数据压缩技术越来越受到人们的重视，图数据的紧凑表示是图数据压缩中的一个重要环节和核心问题.为了更加紧凑地表示图数据，Brisaboa等人[8-9]提出了一种基于k2-tree的表示方法，可以用来紧凑地表示稀疏图.当使用k2-tree表示稠密图时，k2-tree的紧凑性较低，原因是在稠密图中能够用来压缩的“0”单元的数量较少[10].随着图数据规模的增加，k2-tree表示中产生了大量的同构子树[11].针对该问题，董荣胜等人[12]提出了k2-MDD，该方法利用MDD的性质来合并同构子树，进一步提高了图数据表示的紧凑性.出于对时序图数据紧凑表示的需要，2013年，Brisaboa等人[13]提出了kd-tree，kd-tree是k2-tree的d维扩展，用于紧凑表示多维图.2016年，Brisaboa等人[5]为kd-tree提出了2种优化方法：ckd-tree和bckd-tree.无论是kd-tree，还是ckd-tree或bckd-tree，在表示时序图时都存在大量的同构子树.针对该问题，本文提出了kd-MDD，解决kd-tree在表示时序图时出现大量同构子树的问题，进一步提高时序图表示的紧凑性.

2 时序图的kd-MDD表示

k2-tree是一棵用于表示图的邻接矩阵的非平衡k2叉树[9]，是一种能够有效压缩和表示图的邻接矩阵的方法.在k2-tree结构中，树的根节点用于表示整个邻接矩阵，内部节点的“1”表示与叶子节点所在层数对应的邻接子矩阵，且该邻接子矩阵中最少有一个“1”元素，每个内部节点都有k2个子节点.树中的叶子节点可以是0也可以是1，当叶子节点为0时，表示该叶子节点所在层对应的邻居矩阵所有单元格都为0或者该叶子节点对应一个单元格且元素值为0；当叶子节点为1时，表示该叶子节点对应一个单元格且元素值为1.

给定图的n×n邻接矩阵，若n等于k的若干次幂，将其k2等分，即等分成k×k个子矩阵，且每个子矩阵中的单元格个数为n2/k2.当且仅当子矩阵中至少有一个非0单元格时，需要对该子矩阵递归地进行k2等分，直至得到了一个所有单元格都为0的子矩阵或者该子矩阵仅包含一个单元格.若n不等于k的若干次幂，对邻接矩阵的行列进行补0操作，使得矩阵的行列数等于k的若干次幂，再按上述方法构建其对应的k2-tree.

kd-tree是k2-tree的拓展，其被用于处理多维图的多维矩阵，其中d指的是图数据的维度[13].kd-tree的构建过程与k2-tree类似，用kd-tree的根节点表示整个d维矩阵，将d维矩阵递归地进行kd等分，直至得到一个所有元素都为0的子矩阵或该子矩阵只包含一个元素.需要注意的问题是，d维矩阵的每一维度都必须是相等的，并且是k的若干次幂，否则需要进行补0操作，然后再对其进行递归划分，构建对应的kd-tree.

设F是关于n个变量x1,x2,…,xn的多值函数，可以表示为

F:L1×L2×…×Ln→R，

其中,li={0,1,…,li-1}是变量xi可能的取值，R={r0,r1,…,rh-1}是函数F的值域.

为了表示和操纵多值离散函数，文献[14]提出了基于香农分解定理的MDD.MDD是具有多个分支的有向无环树结构[15].如果F表示树结构中每一层的变量集X={x1,x2,…,xn}上的多值表达式，则可以将标记为xi的非终端节点的MDD形式化定义为

其中xi∈X，MDD有h=|R|个终端节点，分别对应于常数r0,r1,…,rh-1.每个非终端节点表示一个具有li=|Li|个分支的变量xi，每个分支对应于一个多值表达式Fxi=j.因此，MDD的每个非终端节点都有一个具体的布尔表达式.

当2个MDD的变量序相同时，这2个MDD可以进行逻辑运算，得到1个新的MDD.假设W=case(a,Wa=0,Wa=1,…,Wa=la-1)和U=case(b,Ub=0,Ub=1,…,Ub=lb-1)是2个MDD，并且它们具有相同的变量序，则W和U的逻辑运算表示为

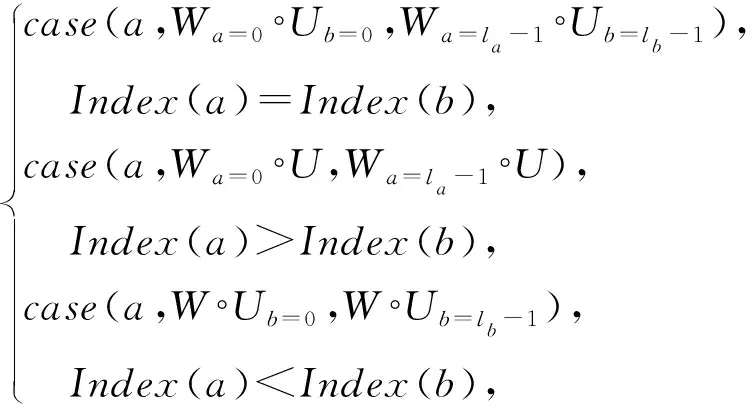
其中,“∘”表示MDD之间的逻辑运算，例如UNION，DIFFERENCE，INTERSECTION等.Index(a)是变量a在给定变量序中的所在位置.

按照kd-tree的思想对多维图的多维邻接矩阵递归地进行kd等分，根据划分结果构建出能表示该多维图的MDD结构，这样的MDD称为kd-MDD.

kd-MDD描述的是一个n元的离散多值函数关系：

f:Z1×Z2×…×Zi×…×Zn→S.

1)n=logkmax(|V|,|T|)，其中V是顶点的集合，T是时间点的集合，max(|V|,|T|)是求2个集合基数中最大值的函数.n的值与对时序图的多维矩阵递归划分的层数相同.kd-MDD的高度为其划分层数加1，即n+1.

2)Zi表示对多维矩阵的第i次划分.Zi={1,2,…,kd}为所有变量的有限值域，与每次对(子)矩阵划分得到的kd个子矩阵一一对应.

3)S是多值函数f的有限值域，即kd-MDD终端节点的取值范围，可以是布尔集合、有限整数集合或有限实数集合，本文取有限整数集合.

kd-MDD结构中包含2种节点：内部节点和终端节点.内部节点用xi表示，包含kd个指向其他节点的指针，这些指针与函数f对应，形式化描述为

fxi=c=f(x1,x2,…,xi-1,c,xi+1,…,xn).

kd-MDD中一个内部节点的图形化描述如图1所示：

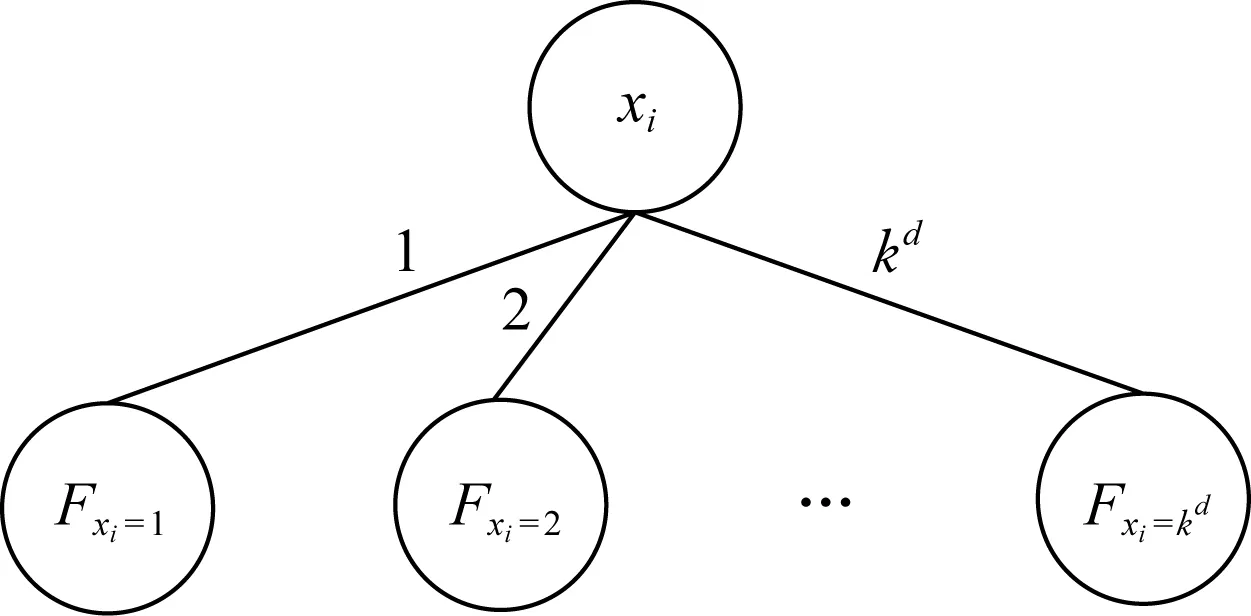
Fig. 1 Graphical description of non-terminal node in kd-MDD图1 kd-MDD中内部节点的图形化描述

从图1可以看出，给定多值变量x1到xn的1组取值，可以得到唯一的终端节点取值.

kd-MDD是一种能够表示多维图的MDD，因此其具有与MDD相同的化简规则，具体有2个规则：

1) 合并规则.合并具有相同值(结构)的终端节点(内部结点).

2) 删除规则.删除那些所有指针都指向同一节点的冗余结点.

图2进一步说明MDD的化简规则，图2中的圆圈表示内部节点，方框表示终端节点，边上的数字表示内部节点的取值，方框中的数字表示函数的取值.图2(a)表示的是一个未化简的MDD，该MDD是关于多值函数f=x×y，x∈{1，2，3}，y∈{1，2，3}，函数f的值域为{0，1，2}.图2(b)是按照合并规则对图2(a)中的MDD进行合并相同终端节点的结果，合并了图2(a)中具有相同值的终端节点，合并的终端节点的传入指针重定向到一个终端节点.图2(c)是按照合并规则对图2(b)中的MDD合并相同结构的内部节点产生的结果，节点y1和节点y2是重复的非终节点，合并为1个节点y1，指向节点y2的指针重定向到节点y1.图2(d)是按照删除规则对图2(c)中的MDD进行删除冗余节点产生的结果，节点y3的所有指针都指向终端节点2，因此节点y3是冗余节点并被删除，指向节点y3的指针被重定向到终端节点2.

Fig. 2 Simplification rules of MDD图2 MDD的化简规则

kd-MDD能更紧凑地表示d维矩阵.大小为n1×n2×…×nd的d维矩阵递归地划分为kd个子矩阵.为了简化分析，假设对于所有的i，ni=n.表1给出了k=2的kd-tree和kd-MDD表示多维矩阵的示例.从表1的第2行可以看出，在多维矩阵的kd-tree中，每个子树都有kd个节点，也就是节点数会随矩阵维数呈指数增加.表1的第3行是多维矩阵的kd-MDD表示，可以看出，不同维度矩阵的kd-MDD节点数没有特别明显的变化.

时序图是顶点之间的连接性随时间变化的图.在时序图G=(V,E)中，V是顶点集合，E是边集合.E形式为(u,v,t)，表示在时间点t时节点u与节点v相连接.T是t的集合，用函数E(u,v,t)描述在时间点t从顶点u到顶点v的边，E(u,v,t)=1表示在时间点t顶点u到顶点v之间存在边，E(u,v,t)=0表示不存在边.时序图的邻接矩阵是多维矩阵，为此，本文提出kd-MDD来紧凑表示时序图.

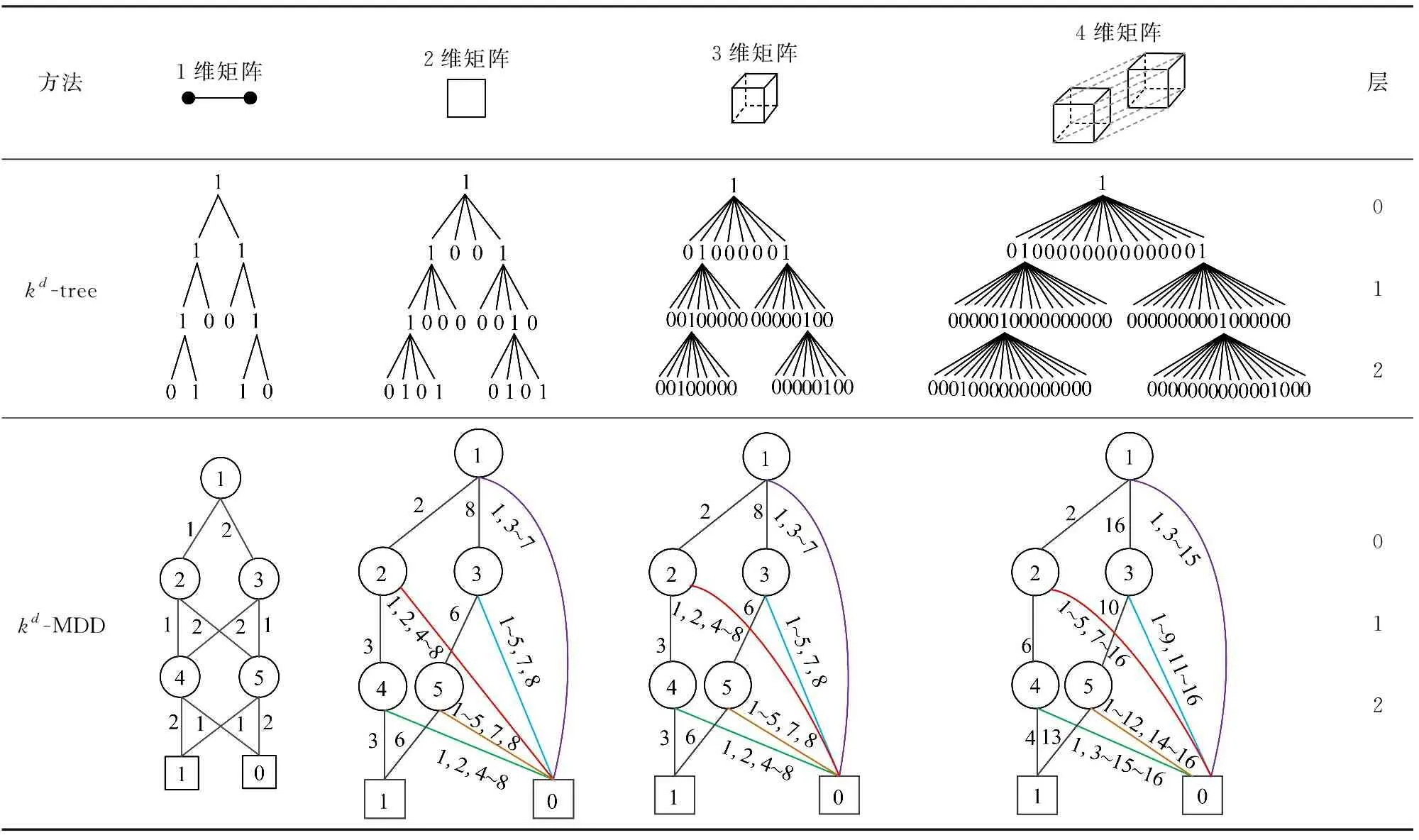
Table 1 kd-trees and kd-MDD for Multidimensional Matrix表1 kd-tree和kd-MDD表示多维矩阵

当时序图稀疏时，其对应的多维矩阵中存在大量的“0”.kd-MDD利用合并规则可消除重复的“0”节点，仅保留一个“0”节点，从而得到稀疏时序图的紧凑表示.当时序图稠密时，利用合并规则和删除规则能够消除大量重复“1”节点和该多维邻接矩阵中存在的大量同构子树，实现更加紧凑的表示.因此，该方法不仅适用于稀疏时序图，也适用于稠密时序图.

在时序图中，max(|V|,|T|)的取值存在2种情况：1)max(|V|,|T|)等于k的若干次幂；2)max(|V|,|T|)不等于k的若干次幂.对于k=2，我们提供2个示例来说明每种情况下kd-MDD的化简过程.该化简过程只是为了说明kd-MDD的化简原理，在实际kd-MDD的构建过程中是直接构建简化的kd-MDD.

例1.max(|V|,|T|)等于k的若干次幂.

对于图3所示的时序图，圆圈中的数字表示顶点，横坐标表示时间，黑色部分表示与之对应的边在对应的时间点存在.对于图3所示的时序图，其3维矩阵如图4所示,其中黑色单元格表示时间点t从顶点u到顶点v的边存在，白色单元格表示该边不存在.

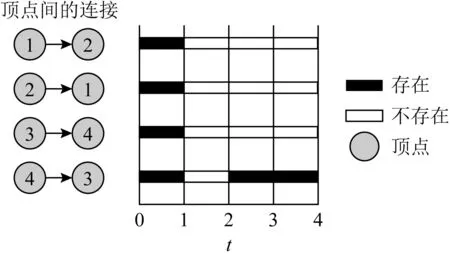
Fig. 3 Temporal graph of example 1图3 例1的时序图

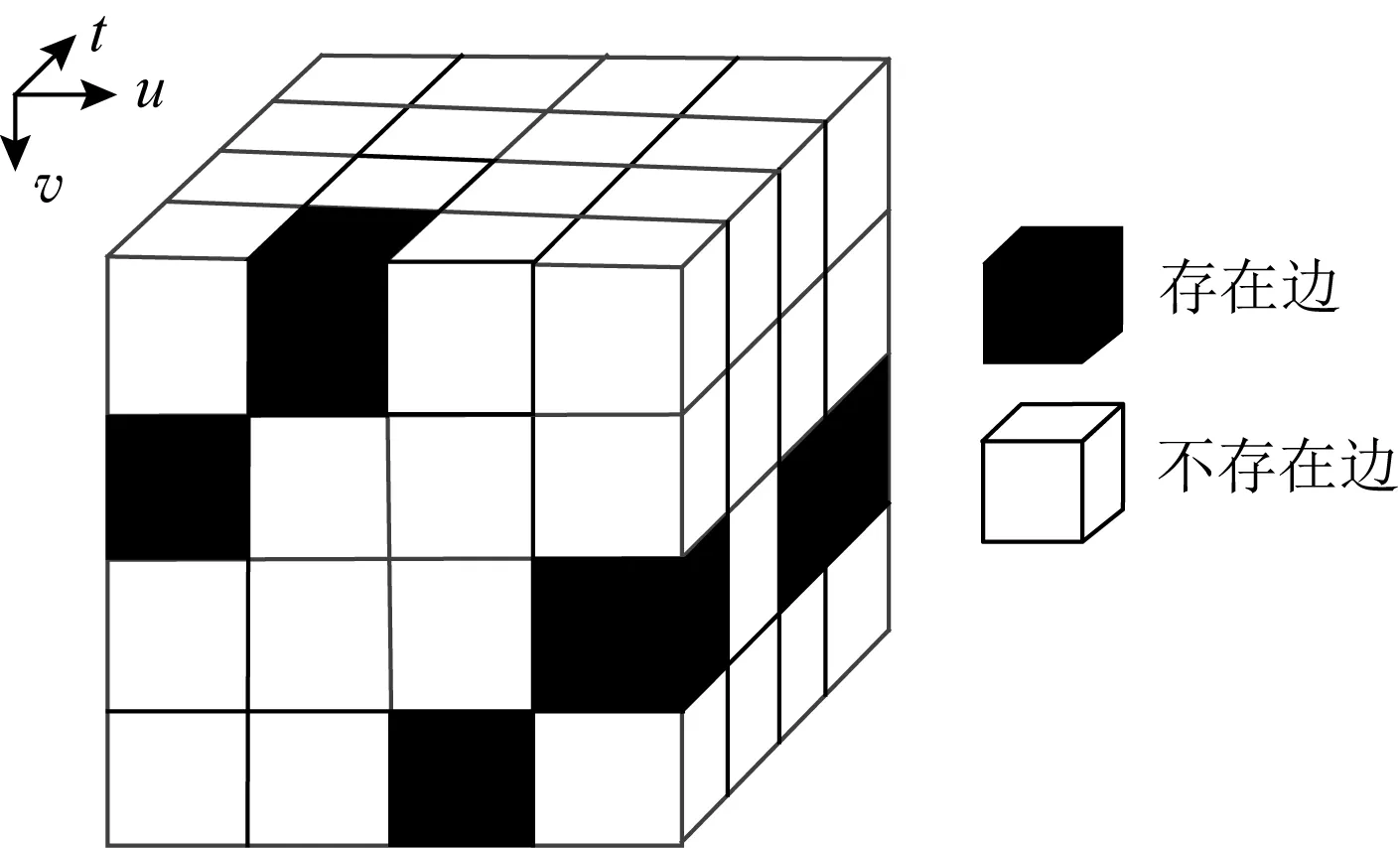
Fig. 4 Three-dimensional matrix of example 1图4 例1的3维矩阵

图5给出了图4所示时序图的3维邻接矩阵的k3-tree表示.当使用k3-tree表示3维邻接矩阵时，3维矩阵等分为k3个部分，并且每个子矩阵包含相同数量的单元格.树的根节点代表整个矩阵，根节点的每个子节点对应一个子矩阵.仅当子矩阵包含至少一个黑色单元格时，子节点的值才对应于子矩阵1，否则子节点的值将为0.将与该节点对应的值为1的子矩阵递归划分，直到子矩阵中每个单元格的值为0或矩阵仅包含1个单元格.从图5能够发现，该k3-tree表示中有33个节点，存在2个同构子树，用矩形框标记.

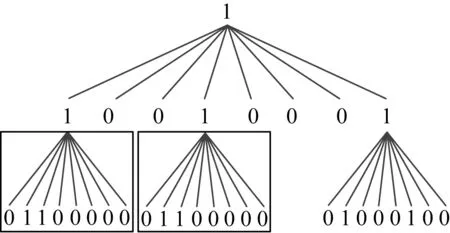
Fig. 5 k3-tree of example 1图5 例1的k3-tree表示

例1中，时序图的3维矩阵的k3-MDD如图6所示，有5个节点.图中节点内的数字仅代表该节点的索引号，不包含有其他意义.

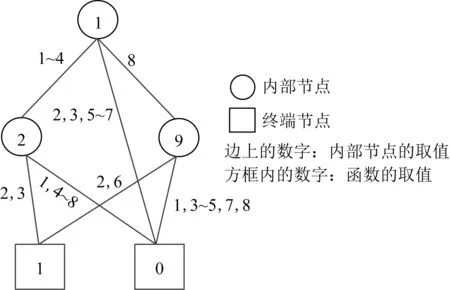
Fig. 6 k3-MDD of example 1图6 例1的k3-MDD表示

例1的k3-tree和k3-MDD表示表明，当将k3-tree转换为k3-MDD时，同构子树被合并，这样节点数量大大减少.例1中k3-tree紧凑表示中节点数为33，而k3-MDD紧凑表示中节点数为5.

例2.max(|V|,|T|)不等于k的若干次幂.

当时序图中顶点数量和最大时间点两者中的最大值不等于k的若干次幂时，可以通过补全矩阵(新增的元素全都标记为0)来满足例1中的条件.图7所示时序图的3维矩阵是5×5×5的，可以通过添加0数据，使原始3维矩阵维数能够整除k3.添加0数据后的结果如图8所示，其中灰色区域表示添加的0数据，黑色单元格表示在时间点t顶点u与顶点v的连接.

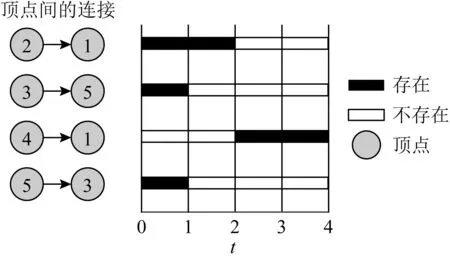
Fig. 7 Temporal graph of example 2图7 例2的时序图

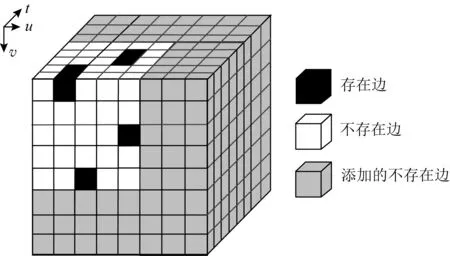
Fig. 8 Three-dimensional matrix of example 2图8 例2的3维矩阵

例2中时序图的k3-tree如图9所示.根据k3-tree的原理，将0数据添加到邻接矩阵，图9中的k3-tree还存在同构子树，这些子树用框标记，相同线型的框为同构子树.在将例2中的时序图的k3-tree转换为k3-MDD之后，节点的数量从65个减少到8个，如图10所示.

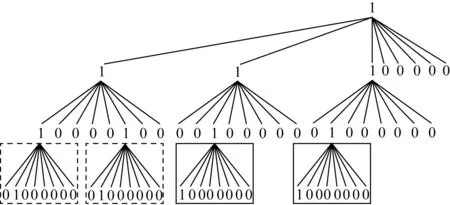
Fig. 9 k3-tree of example 2图9 例2的k3-tree表示

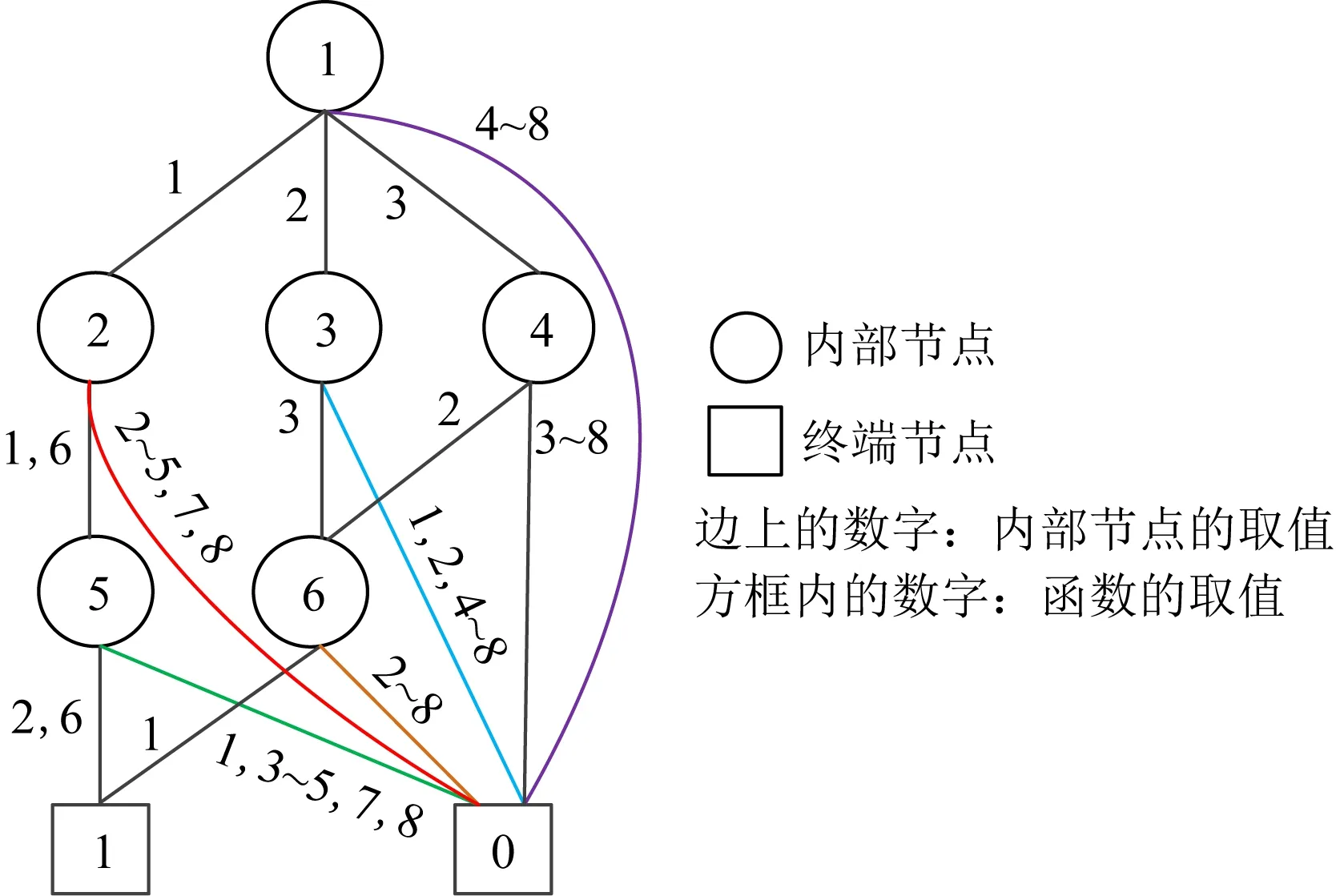
Fig. 10 k3-MDD of example 2图10 例2的k3-MDD表示

3 时序图的kd-MDD构建过程

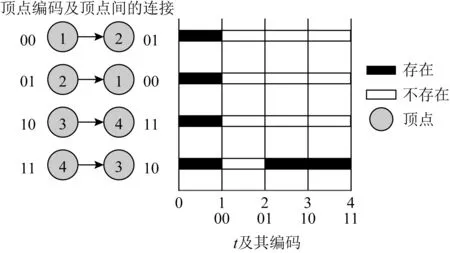
Fig. 11 Codes of vertexes and time points in temporal graph图11 时序图中的顶点和时间点编码

根据董荣胜等人在文献[12]中给出的图的k2-MDD相关构建算法，给出时序图的kd-MDD构建过程，主要包括3个步骤：对时序图的顶点和时间点编码、对时序图的边编码以及根据边编码集合构建kd-MDD.为了更清晰地展示这些过程，以流程图的形式给出相关算法.

3.1 对时序图的顶点和时间点进行编码

构建时序图的kd-MDD时，首先对顶点进行n位的二进制编码，其中n=logkmax(|V|,|T|)，max(|V|,|T|)是max(V,T)取2个集合基数中的最大值.将max(|V|,|T|)递归地进行k等分方式对编号为v的顶点和值为t的时间点编码.当k=2时，在顶点和时间点的n位编码中每一位都是2种状态之一(1或0).对时序图的顶点和时间点的编码过程如图12所示.根据该编码规则对图3中的顶点和时间点进行编码后如图11所示:

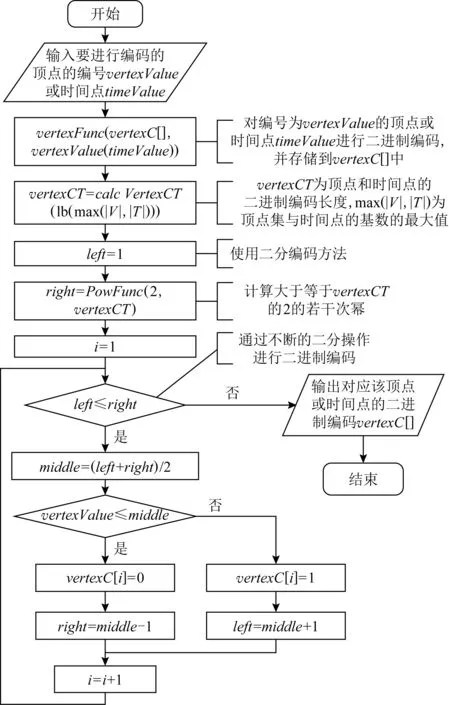
Fig. 12 Coding for vertexes and time points in temporal graph图12 对时序图的顶点和时间点进行编码

3.2 对时序图的边进行编码

在时序图中，在时间点t，顶点u到顶点v的边可以用特征函数E(u,v,t)来描述述.当k=2时，设U=(u1,u2,…,un)，V=(v1,v2,…,vn)，T=(t1,t2,…,tn)是图中顶点和时间点的编码向量，在时间点t，顶点u到顶点v的边的编码可以表示为

eCode:{0,1}n×{0,1}n×{0,1}n→ {1,2,3,4,5,6,7,8}n.

即2个顶点和1个时间点的编码中每一位上的2种状态能够组合出8种不同的状态.因此，时序图中边的编码长度仍然还是n位，每一位对应于8种状态(1,2,3,4,5,6,7,8)之一.边编码过程如图13所示.根据该编码规则以及图11的顶点编码，对图3所示时序图的边进行编码后如图14所示.

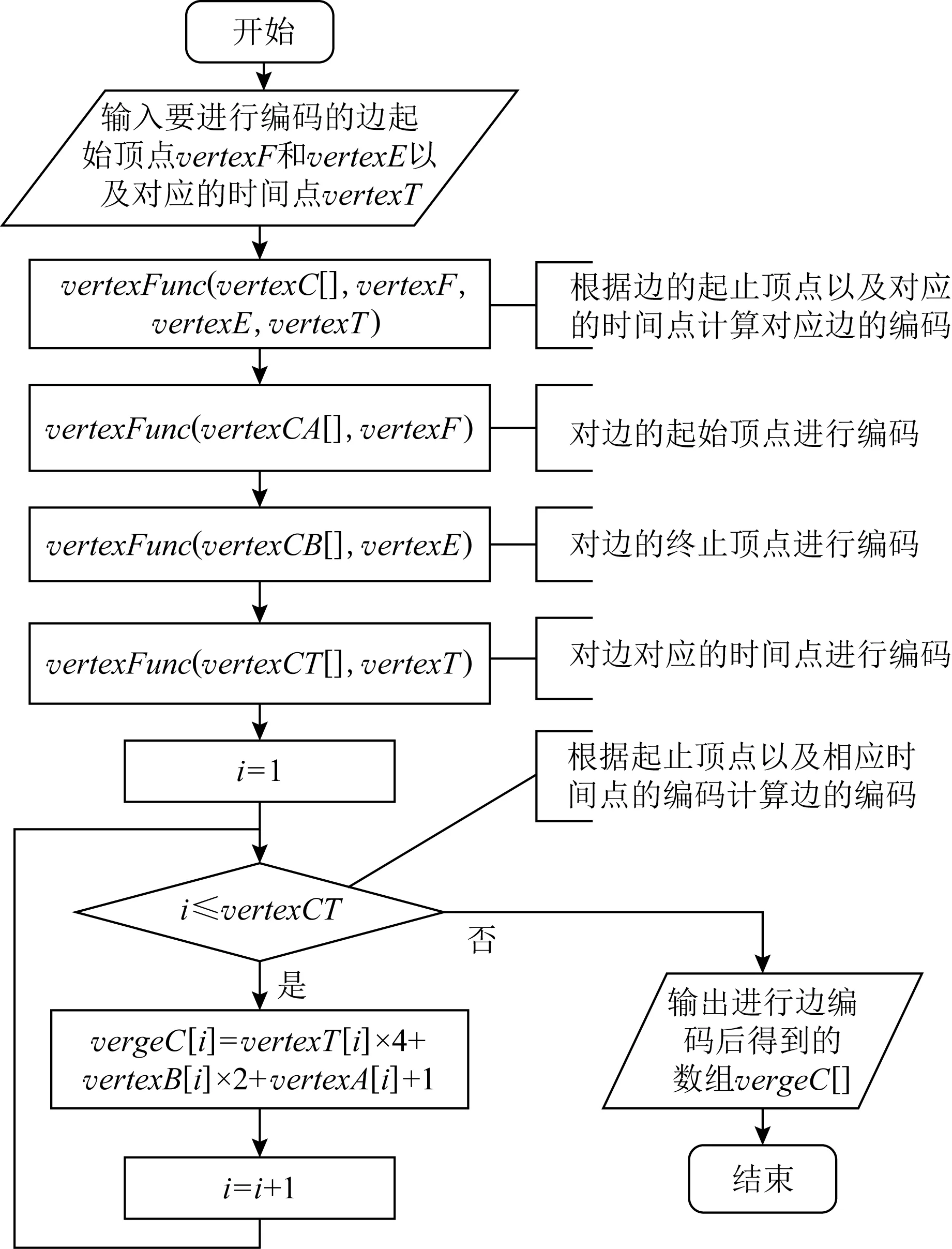
Fig. 13 Coding for edges in temporal graph图13 对时序图的边进行编码

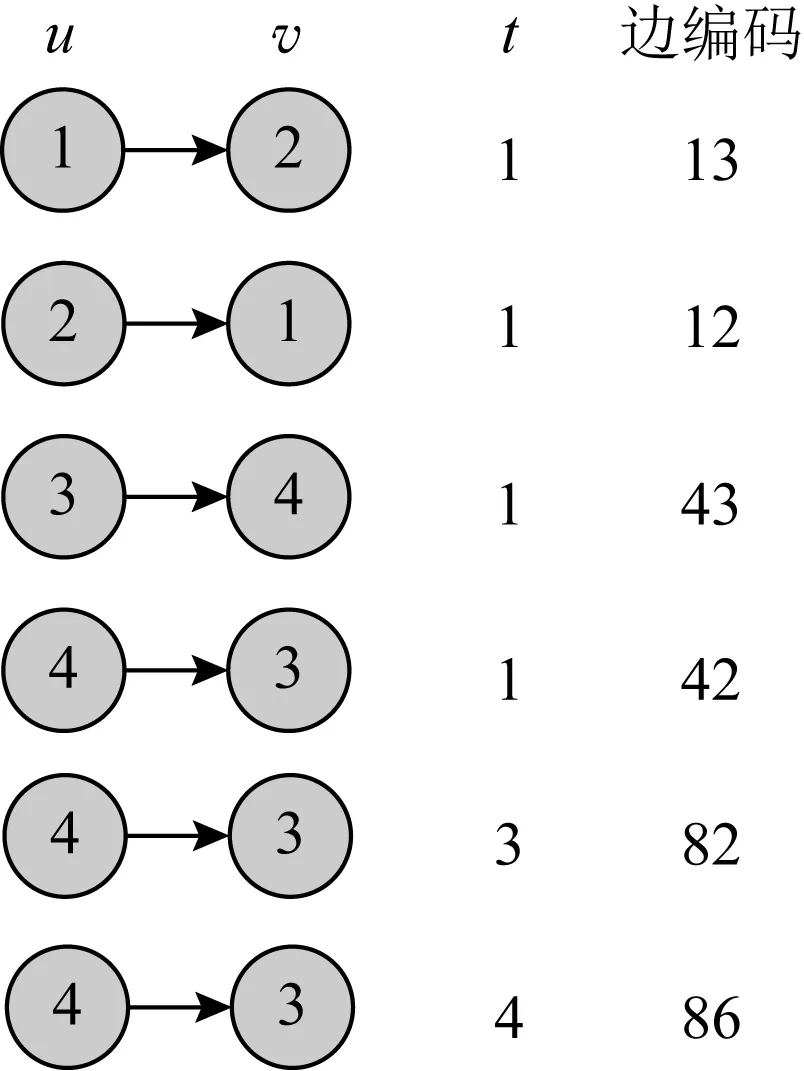
Fig. 14 Codes of edges in temporal graph图14 时序图的边编码

3.3 根据边的编码集合构建kd-MDD

根据kd-MDD的定义，可以构建与边编码相对应的时序图的kd-MDD.如果n个变量的值全部在边集中，则终端节点为1;否则，终端节点为0.例如，根据图13的边编码过程，可以构建对应的kd-MDD结构.在构建kd-MDD时，可以借助爱荷华州立大学在Linux平台下开发的MEDDLY(multi-terminal and edge-valued decision diagram library)函数库，该函数库为构建和操作kd-MDD提供了丰富功能函数.其中，可以用establishRange()函数生成构建kd-MDD时所需的变量个数以及每个变量的定义域；用establishVerge()函数根据给定变量序的1组变量的值生成1个kd-MDD；用apply()函数以及UNION运算将2个kd-MDD进行合并.借助MEDDLY库，我们可以根据边编码生成时序图的kd-MDD.图15给出了构建kd-MDD的过程.

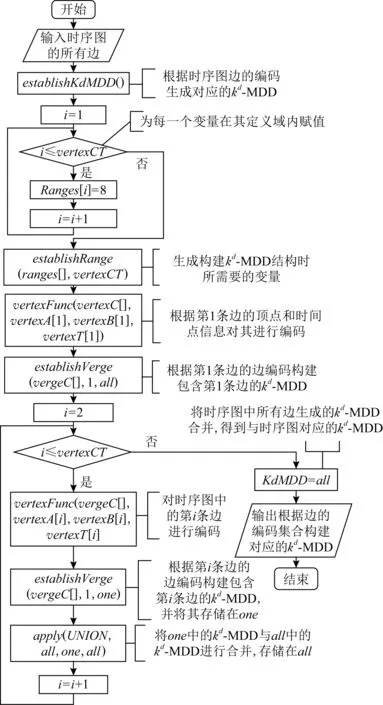
Fig. 15 Constructing kd-MDD图15 构建kd-MDD

4 基于kd-MDD的时序图的操作

构建时序图的kd-MDD之后，可以基于kd-MDD进行以下时序图操作.

4.1 查询边在时间点t的状态

根据边的起始顶点u、终止顶点v以及对应的时间点t的值得到对应的边编号E(u,v,t)，在时序图的kd-MDD中检测E(u,v,t)的函数值，如果得到的值为T，则可判定该边在时间点t存在，反之则该边在时间点t不存在.使用MEDDLY库中提供的INTERSECTION运算求2个kd-MDD的交，可以实现边的状态检测.因此，将原图的kd-MDD与要查询的边生成的kd-MDD进行INTERSECTION运算，查看运算结果是否为空即可，如果结果非空则边E(u,v,t)在时间点t是存在的.查询边在时间点t的状态的过程如图16所示:

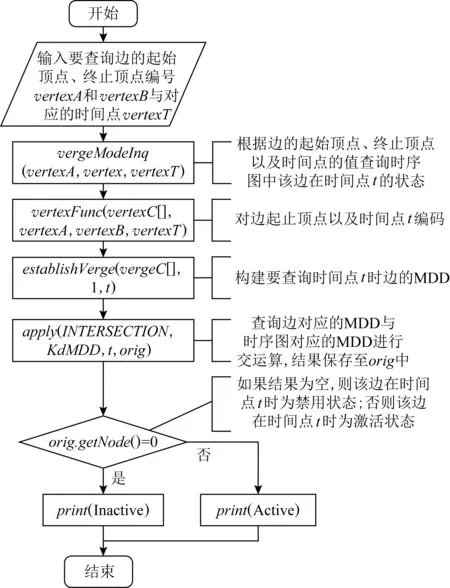
Fig. 16 The state of edge at time t图16 时间点t时边的状态

4.2 查询边在时间点t之后的下一个激活时间点

为了检查边是否处于激活状态，将需要查询的边的起始顶点、终止顶点赋值为u，v，时序图中时间点t之后的时间点依次赋值给t0，检测E(u,v,t0)的函数值.若返回的函数值为T，则该边的下一个激活时间点为t0，反之则不是.

4.3 查询2个顶点之间的连接状态

首先将2个顶点的值赋值给u，v，然后将时间间隔内的时间点分别赋值给t，把2个节点之间的连接在某时间点为激活状态时看作1条边.将这些边看作一个独立的时序图，并为其建立一个kd-MDD.通过将新生成的kd-MDD与原kd-MDD进行逻辑INTERSECTION运算，从而判断给定2个节点之间的连接在时间间隔内是否一直处于激活状态.

高校教师应积极参与校级、省级或全国范围内的各种教学竞赛，如课件制作竞赛，微课教学竞赛，“翻转课堂”教学竞赛等。无论哪一种形式的教学竞赛，对参赛教师都有一定的要求，都需参赛教师进行认真的准备。另外，参赛教师可通过赛事进行交流、借鉴和学习，教学水平和信息素养能力也会因此而得到一定的提高。

4.4 查询在时间点t顶点的直接邻居和反向邻居

在时间点t检索顶点的直接邻居等效于找到所有在时间点t从该顶点开始并终止于另一个顶点的活动边.首先将时间点赋值为t，将要进行直接邻居查询的顶点赋值为u，时序图中的其他所有顶点依次赋值为v，检测E(u,v,t)的函数值.若返回的函数值为T，则该顶点v为u在时间点t的直接邻居，反之则不是.通过统计直接邻居的个数可以得到在时间点t顶点u的出度.

在时间点t查询顶点的反向邻居的方法与在时间点t检索顶点的直接邻居的方法类似.区别在于将查询的顶点赋值为v，时序图中其他所有顶点依次赋值为u.

4.5 添加边和删除边

假设向时序图添加一条边E(u,v,t).根据起始顶点u、终止顶点v和时间点t的代码获得边编码.根据边E(u,v,t)的编码生成边E(u,v,t)的kd-MDD.通过在边E(u,v,t)的kd-MDD和原始时序图的kd-MDD之间执行UNION运算，可以生成增加了该边的新时序图的kd-MDD.

根据要删除边的起始顶点u、终止顶点v和时间点t的编码获得要删除边E(u,v,t)的编码.根据边E(u,v,t)的编码生成边E(u,v,t)的kd-MDD.通过在原始时序图的kd-MDD和边E(u,v,t)的kd-MDD之间执行DIFFERENCE运算，可以生成删除该边后的新时序图的kd-MDD.DIFFERENCE运算是求2个MDD的差，DIFFERENCE(A,B)={x|x∈A∧x∉B}.

5 算法复杂度分析

在构建时序图的kd-MDD时，是基于1组给定顺序的变量的取值组合，变量个数与边的二进制编码长度相同.用n位二进制数对顶点进行编码，其中n=logkmax(|V|,|T|)，即递归地对max(|V|,|T|)进行k等分，实现编号为v的顶点和值为t的时间点的编码.对时序图中单个顶点或者时间点的编码时间复杂度为O(logkmax(|V|,|T|))；在时序图中，在时间点t顶点u到v的边可以用特征函数E(u,v,t)来描述.当k=2时，2个顶点和1个时间点的编码中每一位上的2种状态能够组合出8种不同的状态.因此，时序图中边的编码长度仍然是n位，每一位对应于8种状态之一.对时序图中的每条边进行编码的时间复杂度也是O(logkmax(|V|,|T|))，因此对时序图中所有边进行编码的时间复杂度为O(|E|logkmax(|V|,|T|)).

基于顶点或者时间点以及边编码进行构建kd-MDD时涉及到MDD的构建，其算法复杂度在文献[14]中已经进行了分析，这里不再赘述.

在基于kd-MDD的时序图的基本操作中，由于kd-MDD结构的高度为n=logkmax(|V|,|T|)，因此有关时序图中边操作的时间复杂度为O(|E|logkmax(|V|,|T|))，由此可知有关顶点的直接邻居、反向邻居的查询操作的时间复杂度为O(max(|V|,|T|)logkmax(|V|,|T|)).

kd-MDD可以看做是k2-MDD在三维及更高维度上的扩展，从上述表示方法及算法分析可以看出，kd-MDD结构的宽度相比k2-MDD随着维度的增大成指数级增长，但是其高度并没有变化，基于MDD的特性，kd-MDD在空间复杂度和时间复杂度方面与k2-MDD相当.

6 实验与分析

本文利用MEDDLY库，采用C++语言实现时序图的kd-MDD构建和相关操作.实验用机器配置的软件平台为Ubuntu14.04 LTS 64位操作系统(内核Linux 3.19.0-61-generic)；硬件平台为Intel®CoreTMi5-4690 CPU@3.50 GHz处理器，24 GB内存.测试数据采用公开的真实数据集，实验结果具有更好的代表性.

6.1 实验结果

在真实的时序图数据集上进行了实验.这些数据均来自于KONECT(the Koblenz network collection)[16]，KONECT是由科布伦茨-兰道大学网络科学与技术研究所为研究网络科学而建立的大型网络数据集项目.表2给出了这些时序图的主要特征：名称、类型、顶点数、边数、顶点数与边数的比值以及这些数据集在网站上的文件名.

Out-enron是一个电子邮件网络数据集，该数据包含Enron公司员工及员工之间发送的1 148 072封电子邮件组成，网络中的节点是个体员工，网络中的边是2个员工之间的电子邮件；Flickr-growth和YouTube-u-growth是2个社交网络数据集，这2个数据集包含社交网络的所有用户以及用户之间的朋友关系.

Enwikibooks和Enwikinews是英文维基百科的双向编辑网络，这2个网络包含英文版的Wikipedia用户和页面，用户和页面之间通过编辑事件建立连接.Wikipedia-discussions是一个德国维基百科的讨论主题的数据集，用户之间通过回复建立连接，网络的节点代表德文版本的Wikipedia用户.若数据类型为3维，数据每一列的含义分别是：起始顶点编号、终止顶点编号、边的时间戳.若数据类型为4维，数据每一列的含义分别是：起始顶点编号、终止顶点编号、边的权重、边的时间戳.

社交网络中同一社区内的用户之间的链接比较多，不同社区中的用户之间的链接相对较少，这使此类网络具有2个特征：

1) 本地性.大多数连接都是社区内的.

2) 相似性.同一个社区中的用户的好友集合也是相似的.

针对这些真实数据集的特征，本文提出的kd-MDD存储结构可以充分利用决策图合并同构子树的优势，从而大大减少存储节点的数量.分别使用kd-tree，ckd-tree，bckd-tree，kd-MDD表示这些数据集，表3给出了这4种方法应用于这些数据集的实验结果，表3中的数据为这4种存储结构的节点数.

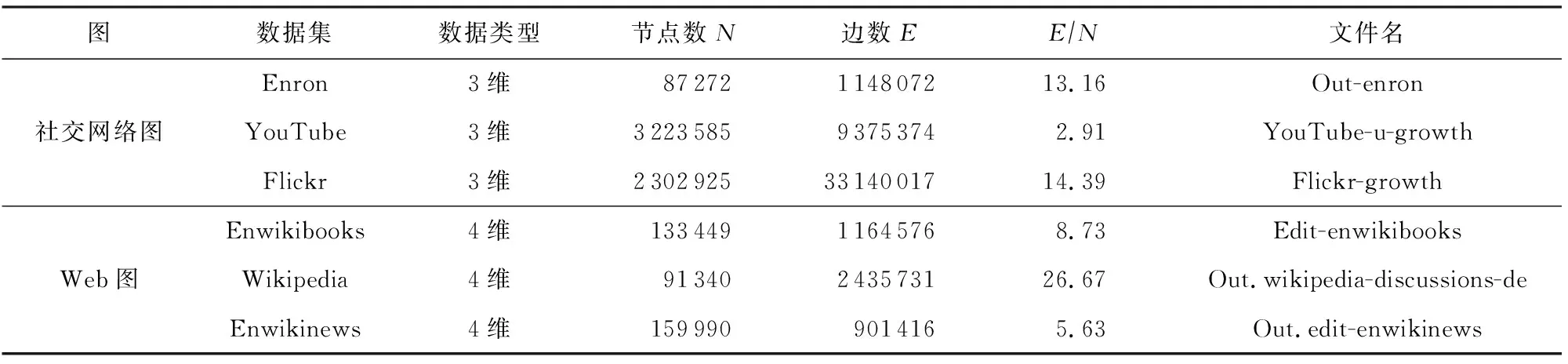
Table 2 Description of 6 Datasets for Testing表2 用于测试的6个数据集的描述

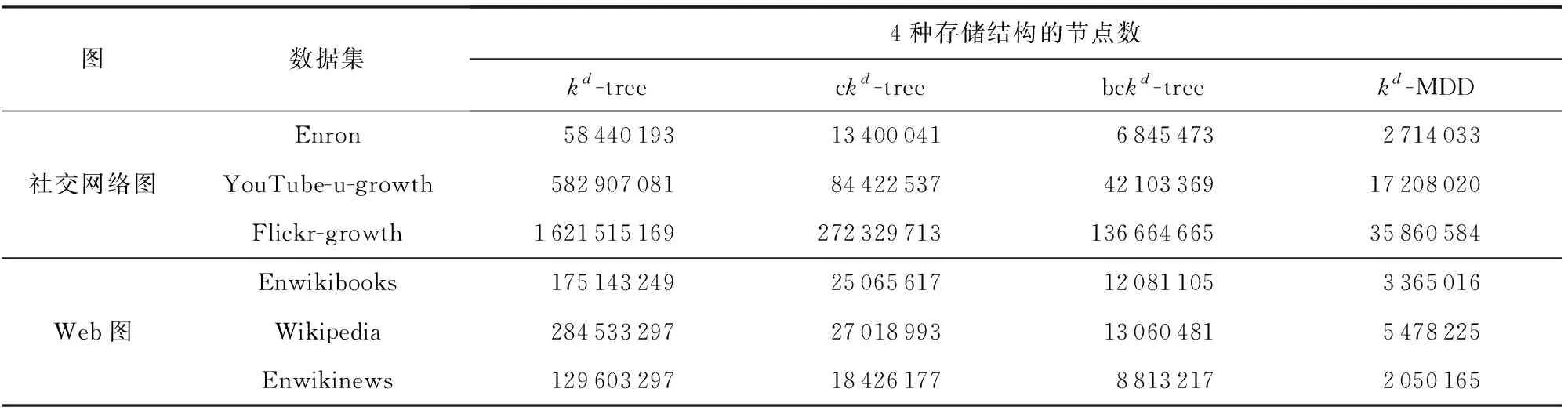
Table 3 Experimental Results表3 实验结果

6.2 实验分析

表3中的实验结果表明，对于6个测试数据集，kd-MDD结构中的节点数仅为kd-tree的1.58%～4.65%，为ckd-tree的11.13%～20.39%，为bckd-tree的23.27%～41.95%.从实验结果可以看出，使用kd-MDD结构存储时序图能大大减少节点数量，实现更好的压缩效果.分析实验结果可知，真实的时序图数据具有较强的稀疏性，同时用户的活跃时间也是相当集中的，因此在使用kd-tree表示时序图时，内部会存在大量的同构子树中，而使用kd-MDD表示时序图时，由于合并了同构子树和消除了大量的冗余节点，使得结构更加紧凑，节点数大大减少，从而节省了存储空间.

在查询时间方面，因为在相同规模的时序图数据集下，kd-MDD，kd-tree，ckd-tree，bckd-tree具有相同的高度，因此kd-MDD中边查询的时间复杂度与kd-tree相同，查询时间基本相同.通过对真实数据集进行实验验证也确是如此.因此，本文未给出kd-MDD与kd-tree在查询时间方面的数据对比.

7 总 结

本文设计并实现了一种更加紧凑表示时序图的方法——kd-MDD，该方法通过将时序图相对应的多维矩阵等分为kd个部分子矩阵，然后将每个部分转换为多值布尔函数.利用决策图的性质，合并了大量的同构子树，获得更加紧凑的结构.在kd-MDD紧凑表示时序图的基础上，继续给出了查询边的状态、查询边的激活时间点、查询顶点的直接邻居和反向邻居、添加边和删除边等基本操作的MDD方法，基于这些操作，可以进行时序图的搜索、最短路、网络流等复杂操作.在真实的数据集上进行了实验，结果表明，kd-MDD中的节点数远远小于kd-tree，ckd-tree，bckd-tree中的节点数，实现了时序图的高效紧凑表示.时序图的kd-MDD表示，既具有kd-tree表示的紧凑性，又能实现符号决策图表示下图模式的高效操作，实现了紧凑表示和高效计算的统一.

作者贡献声明：李凤英负责本文研究方案和实验的主要设计与构建，以及论文主体的写作;申会强参与实验执行和论文的修改;董荣胜参与研究方案设计、实验设计、数据分析和论文修改.