面向GPU计算平台的神经网络卷积性能优化

李茂文 曲国远 魏大洲 贾海鹏

1(中国科学院计算技术研究所 北京 100190) 2(中国航空无线电电子研究所 上海 200241)

近年来，随着卷积神经网络技术的发展，越来越多的算法应用于机器视觉的各种任务中，如目标分割、检测、跟踪、识别等[1].基于深度学习的目标检测算法相比于传统方法通常能实现更高的精确度，因此在各种硬件平台上都得到了广泛的应用，但是卷积神经网络通常伴随着较高的计算复杂度，制约着算法在各个平台上的使用，如何提升和最大化硬件的使用效率来进一步优化卷积神经网络的性能就显得至关重要.另一方面，运行卷积神经网络的这些硬件平台存在一定差异，一种通用、跨平台的工作非常有意义.英伟达公司提供的统一计算设备架构(compute unified device architecture, CUDA)软件支持只适用于英伟达GPU硬件平台，对于其他GPU平台如ARM GPU，AMD GPU等硬件平台来说，开放运算语言(open computing language, OpenCL)[2]是第1个面向异构系统通用目的并行编程的开放式免费标准，也是一个统一的编程环境，便于软件开发人员为高性能计算服务器、桌面计算系统、手持设备编写高效轻便的代码，而且广泛适用于多核心处理器(CPU)、图形处理器(GPU)以及数字信号处理器(DSP)等其他并行处理器.

卷积运算在整个神经网络中占比时间经常在80%以上，在部分主要以卷积进行构建的网络中占比时间能达到95%甚至更高.而卷积操作在访存量和计算量都很大，并且相关工作的算子相对独立难以合并，在深度学习的卷积规模上的优化加速效果有限.针对这些问题，本文实现了一种面向卷积神经网络的卷积优化方法：通过配置相关参数生成各种不同访存、计算规模的通用矩阵乘(general matrix multiplication, GEMM)或Winograd算子，以及算子合并方法对卷积进行优化；结合自调优选择出不同算子中性能最优的算子实现方法，应用到卷积神经网络中，并通过AMD V1605B平台上的实验证明了本文工作的效率.

本文的主要贡献有3个方面：

1) 卷积优化的新方法.针对现有GEMM算法的不足以及深度学习网络规模特点，提出了GEMM优化方法.

2) 在GEMM工作基础上提出Winograd优化方法，并结合算子合并来对卷积进一步优化.

3) 通过自调优的办法，寻找到卷积的最优实现.

1 相关工作和原理

1.1 相关工作

已经有很多文献在软硬件方面提出了针对不同硬件平台、框架实现了对卷积神经网络优化方法[3-4].其中大部分算法是针对卷积神经网络中的卷积层进行优化，卷积有多种实现方式：直接实现、转换成GEMM进行实现，或者通过变换转换成傅里叶变换算法再进行实现.而越来越多的其他平台，比如硬件加速器[5]从硬件角度上解决问题.

凭借着优秀的性能，通过将卷积转换成矩阵乘法GEMM算法来加速卷积，并在此基础上优化GEMM来实现进一步加速成为一种重要的方法.主要的GEMM算法实现有MIOpenGEMM[6]，CLBlas[7]，CLBlast[8]，cuDNN[9]，cuBLAS[10]，OpenBLAS[11]等.英伟达公司的cuDNN软件库与cuBLAS，使用CUDA软件架构，专门应用于英伟达平台的GPU设备，OpenBLAS主要围绕CPU进行优化，两者都不是围绕着OpenCL开展的.基于OpenCL的GEMM优化工作中，深度学习卷积通过GEMM算法提升性能，并结合形如clCaffe[12]等框架执行.AMD公司开发了ROCm平台[13]，其中的MIOpen深度学习软件加速库依靠MIOpenGEMM实现；CLBlas，CLBlast两者针对科学计算应用有着较好的加速，并通过Caffe-OpenCL加速库实现对深度学习的加速.

大部分使用GEMM算法针对神经网络进行加速的性能优化中，都是将GEMM算法作为独立的算子.这些将GEMM算子独立使用的算法库，将GEMM算子独立于整个应用之外，没办法跟深度学习应用进行进一步算子融合，往往限制了整个深度学习应用的性能.

1.2 神经网络与卷积变换原理

常见的基于深度学习的目标检测算法主要分为2类:基于候选区域和基于回归.基于候选区域的深度学习目标检测方法以候选区域为前提，首先在图像中搜索候选区域，再针对产生的大量候选区域进行分类.代表典型方法有R-CNN，Fast R-CNN，Faster R-CNN等算法[14].基于回归的深度学习目标检测方法主要采用回归的方法，将整个目标检测过程视为一个回归问题，不需要花费时间提取多余的候选区域，属于一种端到端的方法.典型代表有YOLO[15]，SSD等方法.

卷积神经网络使用的卷积包含多种参数，使得卷积存在多种类型.对于YOLO网络来说，最常见的是没有特殊参数的普通卷积，计算过程如图1所示.对于不同步长(stride)以及输入的宽度W1和高度H1来说，会有不同的输出W2和H2.

Fig. 1 General convolution图1 普通卷积

普通卷积可以通过图像变换矩阵方法Im2col，将卷积转换成矩阵乘法[16].因为卷积的权重数据是连续存储的，可以直接用于矩阵乘法，所以只需要将输入数据进行变换，将输入的多维数据转换成2维矩阵，即可与权重参数矩阵做GEMM矩阵乘法来实现卷积.从实践来看，GEMM算法可以有效提升方寸的效率和卷积的性能，优化卷积性能的问题也转化成了GEMM算法优化的问题.Im2col中输入数据的具体转换方法如图2所示.

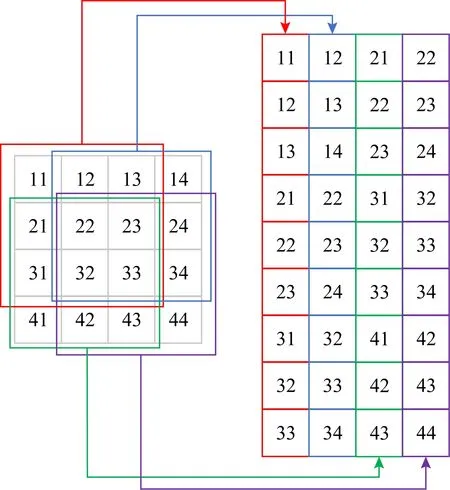
Fig. 2 Im2col transformation图2 Im2col变换

GEMM的一般形式是C=α×A×B+β×C，其中矩阵A和B包含输入数据转换之后的情形.常见的情况是α=β=1，对于GEMM规模为M×N×K来说，矩阵A，B，C是输入，矩阵A的规模为M×K，矩阵B的规模为K×N，矩阵C的规模为M×N.计算过程如图3所示:

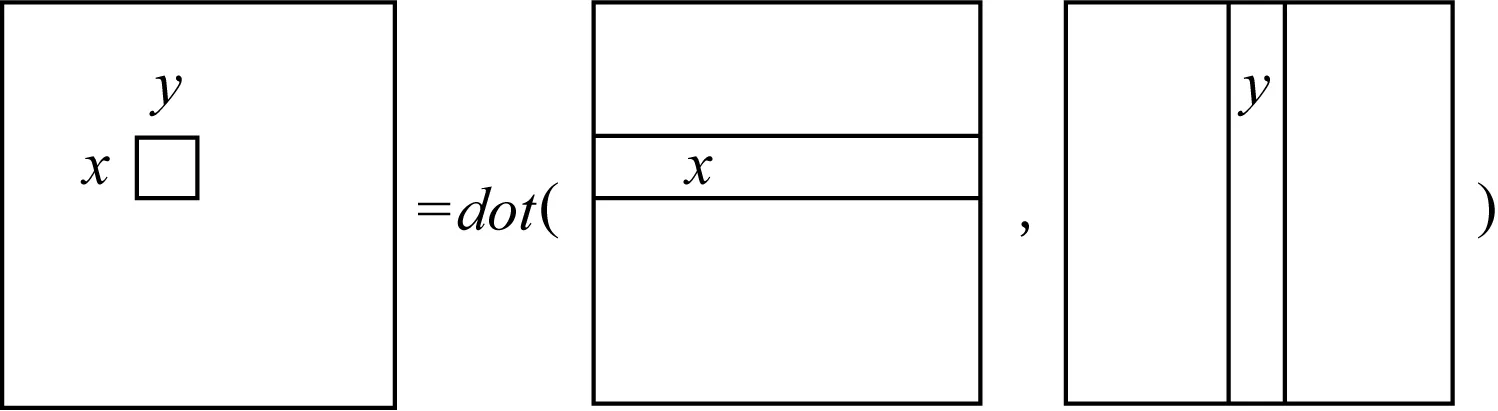
Fig. 3 Cx,y process图3 Cx,y计算过程

当矩阵A,B比较小时，根据计算机体系结构可知，当从RAM中读取矩阵A,B的内存，根据局部性原理可以将矩阵A,B放到缓存(cache)中，因为CPU访问cache比访问主存快.但卷积神经网络中的卷积大部分规模比较大，通常大小会超过cache.当矩阵A,B较大时，即超过cache大小，根据矩阵乘的普通方法，由于访问“行优先存储的矩阵B”的内存不连续(读取矩阵B的1列)，造成缓存cache频繁地换入换出.

普通卷积的伪代码如算法1所示.

算法1.普通GEMM算法.

① forxin [1,2,…,M]

② foryin [1,2,…,N]

③ forzin [1,2,…,K]

④Cx,y+=Ax,z×Bz,y;

⑤ end for

⑥ end for

⑦ end for

因此采用分块的方法来对GEMM进行加速，可以有效地提升cache命中率、增加内存复用，从而提升效率.除了算法1中提到的部分，还需要额外增加分块方法的大小，如图4所示:

Fig. 4 Block computing method图4 分块计算方法

采用m,n,k这3个参数来指定分块,分块将原来的访存空间分成若干个m×n×k的小块，需要执行m0次的按块索引和n0次的循环，在m×n×k的小块内进行GEMM算法并将结果叠加k0次.最终将结果输出到矩阵C.对于通常的卷积来说，M，N，K都是2的幂次，因此m,n,k都可以取8，16等值.具体算法如算法2所示:

算法2.分块GEMM算法.

/*算法中的gemm表示普通GEMM算法*/

①m0=M/m;

②n0=N/n;

③k0=K/k;

④ forxin [1,2,…,m0]

⑤ foryin [1,2,…,n0]

⑥x0=x×m,y0=y×n;

⑦C[x][y]=0;

⑧ forzin [1,2,…,k0]

⑨z0=z×k;

⑩A[x][z]←A[x0,x0+1,…,x0+

m][z0,z0+1,…,z0+k];

k][y0,y0+1,…,y0+n];

B[z][y]);

y0+1,…,y0+n]←C;

最常见的是以景起句。如辛弃疾《卜算子·荷花》的起句，简单的十个字便描摹出了荷花的形态，并运用“红”“翠”两个色彩词，视觉效果即刻突出。再如李处全《卜算子·即席奉女兄寿》，起句中“斗”字的运用让芍药有了拟人化的动态效果，正似“对镜贴花黄”的娇娘子；而“飞”字又巧妙地借“飞雪”之轻盈飘渺的姿态给人以想象空间，顿感三月杨柳飘絮正如寒冬之雪花。再如范成大《卜算子·云压小桥深》，开篇“云压”二字就为全诗奠定感情基调，为下文梅花被雪压不已，又再次布满横窗影的遭际张本，即被雪压不已，又再次布满横窗影。

YOLO目标检测方法中，使用的主要是普通卷积，因此将其转变换成GEMM是一种主要的优化方法，但存在一些问题，以YOLOv2的网络模型为例来说明.表1所示的是共30个网络层的YOLOv2网络模型中的卷积层及其变换成GEMM以后的参数，其中进行计算的矩阵A的规模为M×K，矩阵B的规模为K×N.

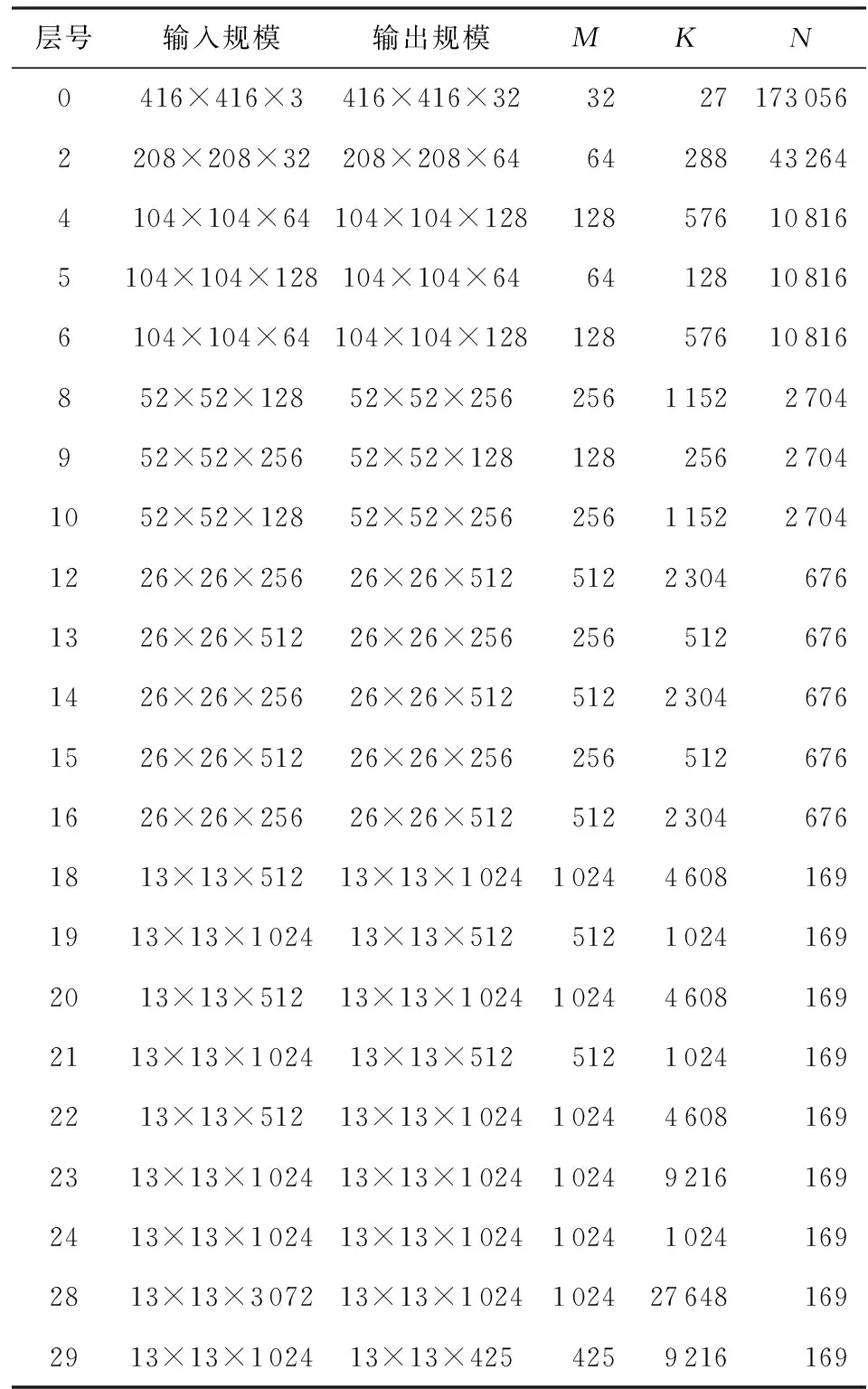
Table 1 Calculation Parameters After ConvolutionConversion GEMM Algorithm表1 卷积转换GEMM算法后的计算参数

表1的数据能够明显看出4种情况：

1) 计算参数变化大，存在极小值、较小值情况.M,N存在较小值的情况，比如N=169和M=32.而现有的GEMM算法加速库的访存分块规模更多考虑大规模矩阵计算，这使得对于M，N，K只有部分较小时，针对大规模矩阵乘法的分块、访存、计算的方法，会存在计算、访存资源不能够充分利用的问题.

2) 分块参数不能被整除，存在计算分支.进行GEMM运算，在M,K,N不能被整除时，并行计算存在余数分支的问题.常用的GEMM算法加速库生成算子时只生成M,K,N都存在余数分支或者都不存在余数分支这2种情况，不讨论M,K,N其中仅有部分参数存在余数分支的问题.而深度学习卷积中，通常仅有N参数有较常见的分支，对所有参数都进行分支判断会造成计算资源的浪费，影响并行效率.

3) 计算参数比例变化大.进行GEMM运算的2个矩阵的形状和参数比例是不断变化的，比如第0层网络层的矩阵A的M,K很小，均不高于32，但N非常大；第28层网络层中，M,K非常大，而N非常小.现有的GEMM算法加速库的访存分块大小又通常为1∶1的正方形，如32×32,64×64等，这使得访存计算低效.

4) 只优化卷积，无法进行多算子合并.常用的GEMM算法加速库生成的时候只能使用卷积算子，无法进行多算子合并，影响网络效率.

2 卷积优化加速方法

2.1 GEMM优化原理

算法3.本文面向GPU的GEMM算法.

/*算法中lut表示读取配置信息，Synchronize(thread)表示对GPU线程进行同步*/

①m,n,k,gtx,gty←lut(M,N,K);

②m0=M/m,n0=N/n,k0=K/k;

③mthr=m/gtx,nthr=n/gty;

/*设置工作组(thread_group)规模为(m0,n0),每个工作组id为(gx，gy),在每个工作组内设置共享内存AS[m][k],BS[k][n]*/

④ forthread_group(gx，gy) inrange(m0,n0)

⑤ 共享内存AS[m][k],BS[k][n];

/*每个工作组内工作项(thread_item)规模为(gtx，gty)，每个工作项id为(tx，ty),每个工作项设置本地数组

CL[mthr][nthr]*/

⑥ forthread_item(tx，ty) inrange(gtx，gty)

⑦ localCL[mthr][nthr];

⑧x0=gx×m,y0=gy×n,CL[1,2,…,mthr][1,2,…,nthr]=0;

⑨ forzin [1,2,…,k0]

⑩z0=z×k;/*将数据块从CPU传

到GPU共享内存*/

xi×gtx][z0+zi]×

BS[z0+zi][ty+yi×gty];

其中thread_group表示在OpenCL实现中工作组的分组，thread_item表示每个工作组中的工作项，memory_barrier_among_thread()同步不同线程之间的操作.但是如表1所示，存在着较多的N不为16倍数的情况，因此对于GEMM算法来说就产生了很多的分支和判断，降低了算法的并行度和效率.同时硬件的访存效率对GEMM算法的影响也至关重要，对于M,N较小的情况来说，采用固定大小进行分块来实现对不同尺度的、规模的矩阵进行支持，也显得不够.

为了解决表1中存在的问题，并进一步提升并行算法效率，我们在工作中采用代码生成的策略.即增加对各种不同类型的算法参数进行配置，通过特异性的算法参数来解决不同规模下的GEMM算法性能问题，主要包括3种配置方式：

1)m，n，k分块参数可变、可配置

对于算法2中进行分块的参数m，n，k，不再采用固定值进行配置和计算，而是可变参数，使得分块大小能够提高访存效率.

m，n，k参数跟gtx,gty有关，同时要考虑执行算法硬件的硬件参数.针对常用的GPU架构，m，n，k取值范围通常为16的整数倍.而k的取值对分块的影响有限，主要是对循环的影响较大，因此需要配置较多参数的主要是m，n，而且需要配置足够多的m，n.

2)M,N,K余数计算分支可变、可配置

规模不为整数倍会导致存在分支，但卷积神经网络的参数并不是M,N,K都会导致分支存在，因此根据参数情况去配置算法执行分支的部分变得尤为重要.

m，n，k取值为16的整数倍，当不为16的整数倍时，往往M,N,K存在着余数，因此需要执行分支语句来完成对边界的正确运算以保证正确性.分支对于并行异构设备往往造成了运算资源的浪费，因此需要尽可能减少分支存在的情况，生成存在尽量少的分支代码.

3)gtx,gty访存计算比例

常用的访存、计算比例通常为1∶1，即缓存AS,BS这2个矩阵的数据每次采用8×8，16×16，32×32，64×64这样的分块访存、缓存、计算的规模，但对于可变参数来说，可能遇到比例不一致的情况，如分块、计算的规模为32×64等，也产生了相应的分支和算法配置.

由于各种参数对代码的影响因素较多，因此对于不同的M，N，K，正确选择GEMM算法配置的参数，能够使得GEMM运算效率最大化至关重要.

根据算法需要执行的数据规模，即M,N,K大小，生成所有可用的GEMM算法代码以后，遍历所有的GEMM算法代码，寻找到最优性能的配置保存下来.在卷积神经网络执行推理时，通过LUT函数读取配置.

2.2 Winograd优化原理

基于2.1节中的GEMM优化原理，本文提出了通过一系列变换以及GEMM算子来实现Winograd算法并实现卷积优化加速的方法.

Winograd算法越来越多地被应用在了卷积加速上[17].Winograd算法在计算设备上进行加速的主要原理是使用了更多的加法来代替GEMM算法的乘法，从而提高在计算机设备上的性能.Winograd算法的原理与证明过程在此不再赘述，主要介绍适用于卷积的Winograd，以输入数据d为4×4、卷积核心g为3×3的卷积为例，输入d,g，输出Y为

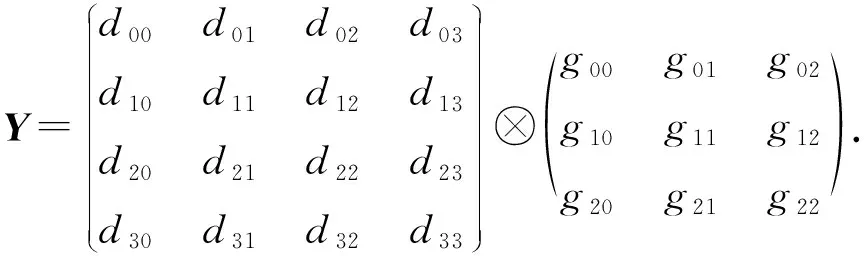
(1)

卷积的实际计算中，把卷积数据分为4×4的数据块，针对每个块应用F(2×2,3×3)的计算公式，从而可以降低运算强度，提高性能.其中，参数2×2意味着从输入数据矩阵上面滑窗的步长为2×2，参数3×3意味着卷积核心为3×3的规模.使用Winograd的F(2×2,3×3)计算为

Y=AT((GgGT)⊙(BTdB))A.

(2)

其中，中间变量G，BT，AT分别为

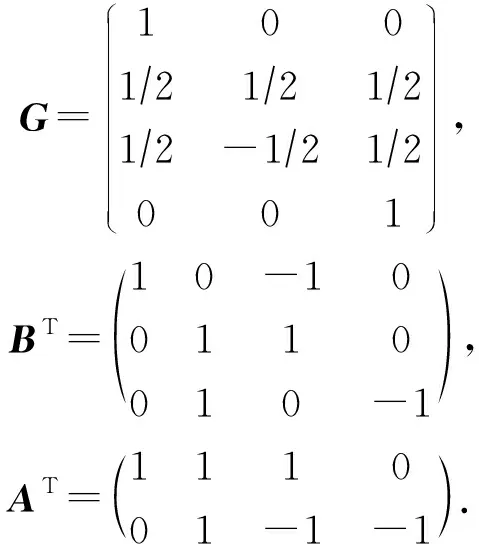
(3)

该算法进一步拆分成4个步骤：

1) 卷积核心GgGT变换

对卷积核心(kernel)g进行变换:

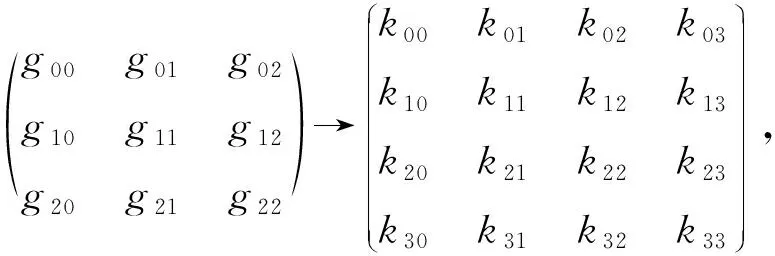
(4)

其中，列对应于输入通道，行对应于输出通道.表格中的每个元素包含了16个数值4×4,也就是按照公式GgGT从一个3×3的核心中计算出来的值.对于进行多次处理、视频处理等情况，卷积核心变换后的数据可以复用，以提升速度.变换后的结果为

1 2 …cin

2) 输入数据BTdB变换

对输入数据进行变换时，先将输入数据重组视为1个矩阵数组，行数为cin，将每一行连续拼接，共有len1列，其数据存储为

1 2 …len1

对于第1行第1列的矩阵d进行变换后BTdB的输出为

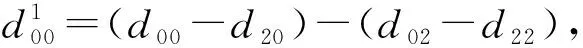
1 2 … (w2+1)(h2+1)/2

3) 4×4规模点积

无论是卷积核心还是输入数据，变换后的结果都是4×4规模的数据.卷积的执行过程中，输入数据为w1×h1×cin规模，输出数据为w2×h2×cout，会产生cout×cin组4×4规模的卷积核心变换，以及cin×floor((w2+1)/2)×floor((h2+1)/2)组4×4规模的卷积输入数据变换.因此产生cout×cin×floor((w2+1)/2)×floor((h2+1)/2)次4×4规模的点积，可以转换成4×4次即16次的矩阵乘法，直接调用算法1.

4) 计算结果ATCA变换

通过对4×4规模点积的计算结果C进行ATCA变换，获取最终的输出Y.

2.3 算子合并

卷积在进行运算时，通常跟后续的算子操作有一定的关联，因此可以进行算子合并.通过将算子合并，在OpenCL软件中有诸多好处：

1) 可以节省存储中间结果的空间；

2) 减少对内存的读写；

3) 减少函数的调用与内核启动(kernel launch)时间.

卷积的数学表达式是yconv=w⊗x+b，可以与卷积进行合并的算子主要有3种方式：

1) 与batchnorm进行合并

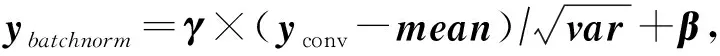
2) 与激活函数合并

激活函数activate是一类函数，常用的激活函数有sigmod，tanh，ReLU，LeakyReLU，ReLU6等.激活函数通常的算式是yactivate=activate(yconv)，融合以后新函数公式是yactivate=activate(w×x+b).

3) 与eltwise合并

eltwise算子的操作有3个：点乘(product)、相加(sum)、取最大值(max).由于卷积转换成GEMM算法，GEMM计算的表达式为C=α×A×B+β×C，可以和eltwise算子进行合并，当进行eltwise算子的sum操作时，eltwise算子为yeltwise=yconv+x1，与GEMM公式合并以后的结果为C=A⊗B+C.

3 神经网络与卷积自适应调优优化

第2节生成了各种规模的GEMM算子，还需要结合神经网络参数进行自适应调优，选择出性能最好的卷积算子，以便于完成卷积神经网络的处理.

3.1 神经网络配置

通过神经网络的配置，获取卷积与网络的配置信息，分析、计算卷积对应的变换后的GEMM和Winograd参数信息，以及计算算子合并的信息.为后续算子合并、生成GEMM代码提供足够的配置信息和参数信息.整个网络的处理流程如图5所示：

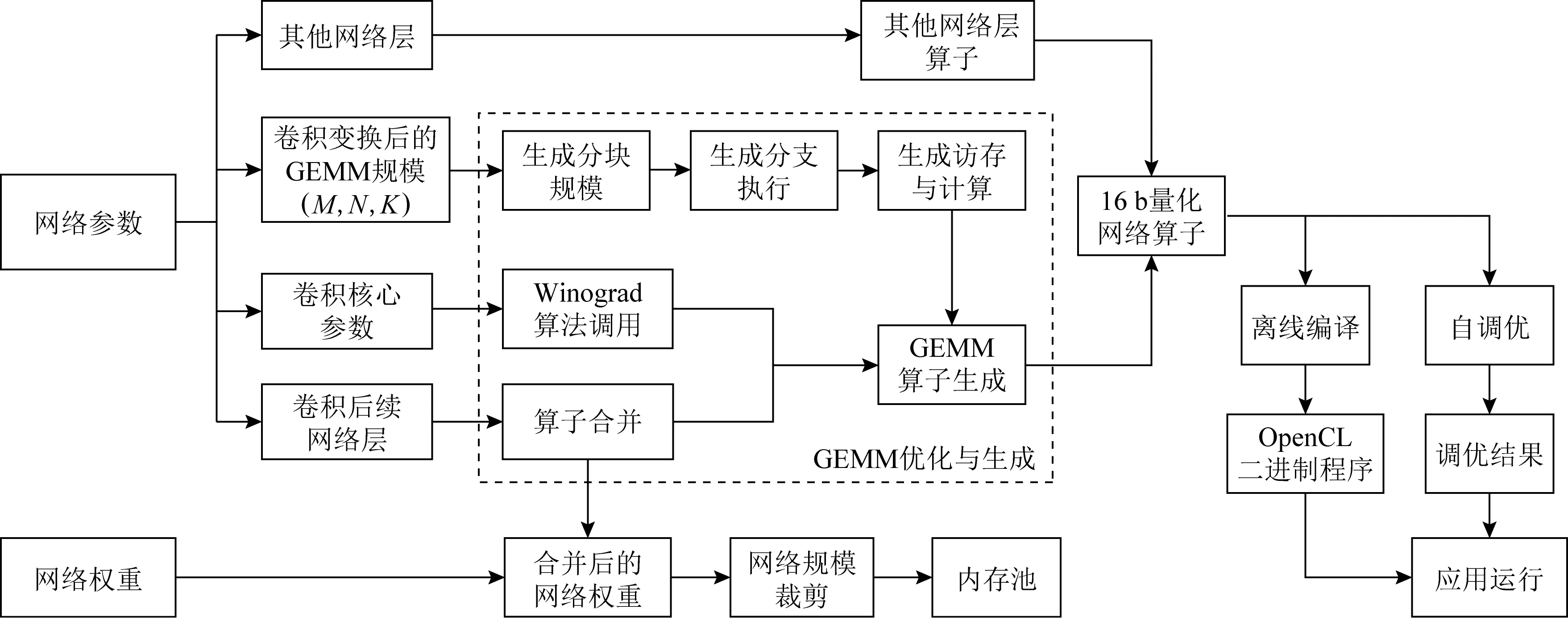
Fig. 5 Neural network convolution optimization process based on OpenCL图5 基于OpenCL的神经网络卷积调优过程

3.2 GEMM优化生成与卷积自调优

卷积神经网络中的GEMM代码配置因素较多，主要包括6个配置方面：

1)m,n,k分块规模

根据GEMM规模(M,N,K)来进行配置.

2)M,N,K执行分支

根据GEMM规模(M,N,K)来进行配置.

3)gtx,gty访存计算比例

根据GEMM规模(M,N,K)来进行配置.

4) 是否用于Winograd

根据卷积核心参数进行配置.

5) 算子合并

根据卷积后续网络层情况进行配置.

6) 网络16 b量化

根据需求是否适用16 b量化.

由于GEMM代码配置因素多，因此生成的不同规模下、场景下的GEMM代码非常多.为了实现GEMM算法的效率最大化，采用自调优的办法.即在生成了网络算子以后，还需要对网络进行自调优，得到该网络的GEMM效率最优的参数.网络调优采用遍历调优的方法，对所有可能的算子进行测试和运算，对于可能执行Winograd的卷积，将Winograd实现也一并进行对比，将对比得到的最优输出结果的配置参数输出为调优结果，便于运行时进行调用.

3.3 OpenCL离线编译

在线编译是指在宿主程序中引用内核的源代码来构建OpenCL程序.进行在线编译时，内核通过运行时环境中的OpenCL API库编译内核函数的源代码.这种方法不适用于需要达到实时效果的嵌入式系统.同时，由于内核程序可以从主机程序中读取，因此不适合商业应用.离线编译是指OpenCL主机可以直接在目标设备上运行编译好的二进制程序.离线编译时，内核程序使用OpenCL编译器预先编译二进制文件，OpenCL API在宿主程序中调用编译后的二进制文件.由于二进制执行文件是在主程序中直接调用的，所以从主程序启动到内核运行之间的时间非常短,能够有效提升框架的速度和性能.

3.4 内存池

在卷积神经网络进行推理时，使用的数据量较大，占用较多的内存资源；同时对于临时数据的变换也需要存储空间，会造成频繁的内存申请和释放.

通过使用内存池的方法，可以有效提升内存空间的复用率，减少内存空间占用.同时避免了变换产生的临时变量频繁的申请和释放,可以有效节省内存开销，提升内存使用率，避免无用的时间浪费.

3.5 网络规模裁剪

由于卷积神经网络的计算复杂度和存储空间与图像的大小成正比，但是卷积神经网络的输入规模配置经常和图像大小不一致，产生了一部分的计算冗余、资源浪费.在预处理时，很多图像都有一定的比例，这与神经网络的输入不一致.特别是在处理摄像机或者视频时，比例通常是16∶9，多余的部分必须填充到黑色区域，这样会产生很多无用的计算，修改网络的输入大小，以适应16∶9的大小，可以有效地提高数据利用率和网络速度.

3.6 16 b浮点量化

16 b浮点是指2 B大小的浮点类型.相对于32 b浮点，精度有效位数只有3或4位左右.对于卷积神经网络，训练使用16 b浮点会导致训练效果下降，甚至得不到理想的模型.但对于经过32 b训练出来的网络模型，削减精度使用16 b的结果，与32 b的输出效果相差不大，也避免了模型重新训练、开发、转换的问题.

随着加速设备的发展和迭代，支持16 b浮点的硬件设备已经越来越多.使用16 b浮点来代替32 b单精度浮点进行计算，能有效保证浮点精度避免定点化带来的精读损失.同时对比32 b的单精度浮点，可以减少50%的内存空间并提升访存效率.对于支持16 b浮点计算的硬件设备来说，可以提升计算效率.

4 实验结果与分析

实验测试的硬件平台包括AMD V1605B APU与英伟达嵌入式GPU SOC TX2.AMD V1605B APU含有一块Ryzen 嵌入式V1000系列CPU，主频2.0 GHz，最大可达3.6 GHz主频，以及1片Vega 8 GPU，有8个CU；TX2是一块嵌入式SOC，包含双核 Denver 2 64 位 CPU 和4核 ARM A57 Complex，以及1片NVIDIA PascalTM架构GPU，配有 256个NVIDIA CUDA核心.

实验测试的对照软件包括MIOpenGEMM，CLBlas，CLBlast，darknet采用的操作系统是Ubuntu 18.04.3，驱动为AMD官方Vega显卡驱动.

4.1 GEMM算法对比

除了本文提出的GEMM算法，还对比测试了多种基于OpenCL的GEMM算法，包括MIOpen-GEMM，CLBlas，CLBlast.其中gemm0和xgemm都是来自MIOpenGEMM的GEMM实现.差别在于是否适用额外的矩阵变换.测试如图6所示:

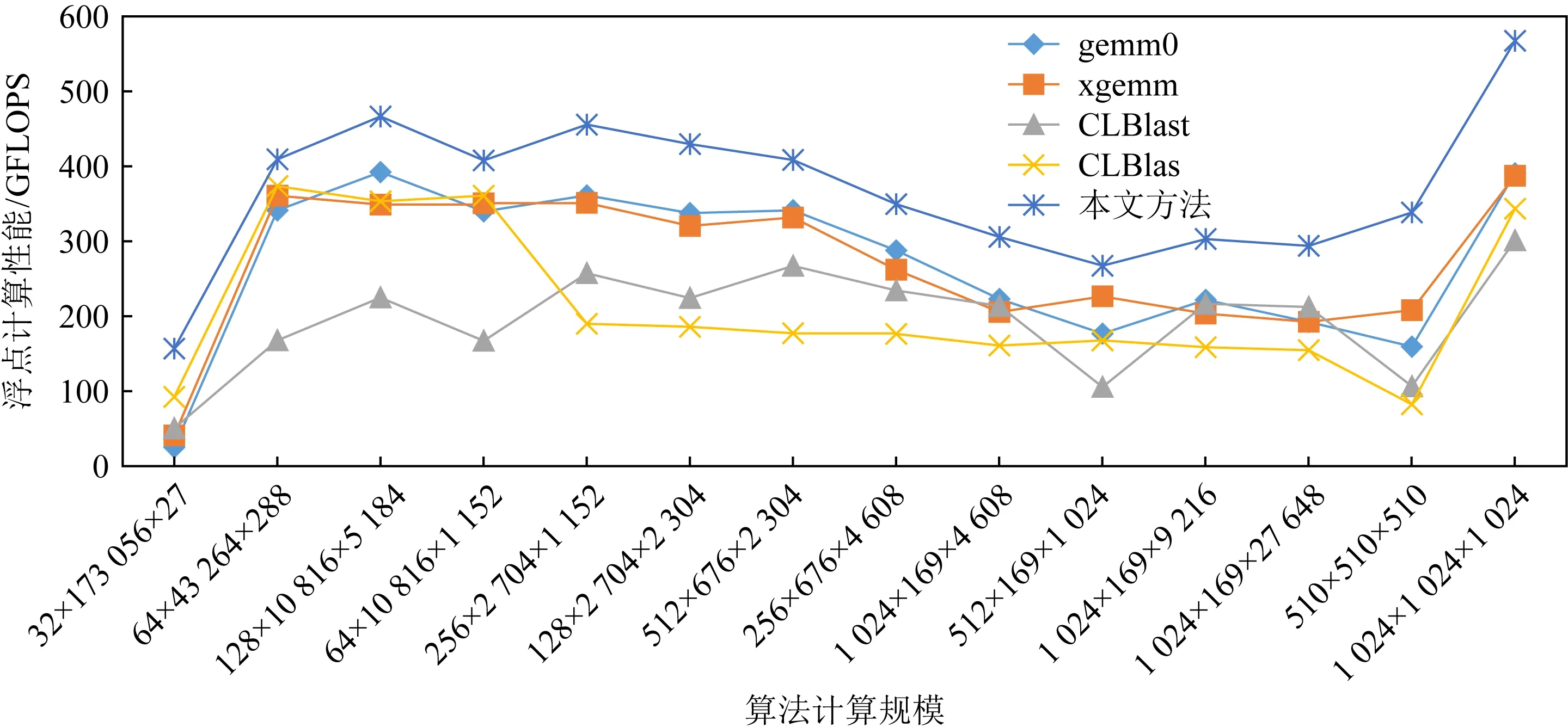
Fig. 6 GEMM algorithm performance test图6 GEMM算法性能测试

从对GEMM算法的对比测试可以看出，深度卷积神经网络中使用的卷积转换成GEMM以后，这些规模的计算效率在当前的各个软件算法库中性能表现都远低于1 024×1 024×1 024这种方形矩阵乘法的计算效率,而我们的方法针对于卷积神经网络中的规模能够有效地提升效率；同时对于1 024×1 024×1 024这种矩阵乘法，也有显著的计算效率提升.

4.2 GEMM和Winograd实现卷积效率对比

Fig. 7 Winograd algorithm performance test图7 Winograd算法性能测试

对Winograd算法进行测试，结果如图7所示.在进行GEMM和Winograd对比时，因为Winograd的变换包含了对卷积核心的变换，因此在测试GEMM和Winograd的性能时，采用卷积的规模进行测试和比较，计时标准为耗时.即在测试时，分别测试使用Im2col+GEMM的性能以及Winograd完成卷积的性能.

测试时使用的数据输入输出都为13×13规模，变化输入和输出通道数进行测试.可以看出：GEMM耗时较长，而Winograd算法耗时较少.

4.3 神经网络推理性能对比

通过对比和测试TX2上运行YOLOv3等网络的效率(使用darknet框架与cuDNN软件)和AMD V1605B上运行YOLOv3等网络的效率(使用本文方法)，来对比对卷积神经网络推理性能的加速情况，以及对比使用CLBlas实现GEMM的效率，和本文实现的FP32和FP16(16 b量化)的效率.对于卷积神经网络中满足Winograd算法使用条件的，本文都采用了Winograd算法进行实现.测试结果如表2所示：

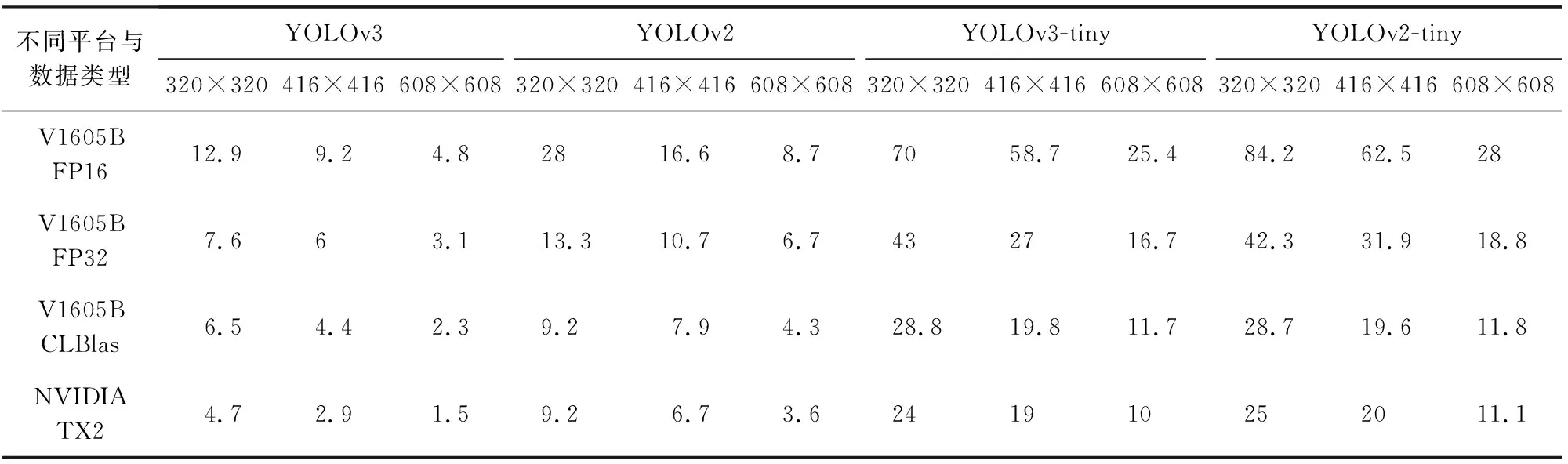
Table 2 Neural Network Inference Performance Test表2 神经网络推理性能测试

5 结束语

本文以现有的GEMM算法在卷积神经网络应用中的不足为出发点，有针对性地分析、加速GEMM算法.并以本文优化后的GEMM算法为基础，实现了Winograd算法，并通过Winograd算法进一步对卷积进行加速.还提出了基于OpenCL的卷积神经网络优化框架，借助优化后生成的GEMM算法自调优、16 b量化等，从框架上对卷积神经网络进行了进一步的加速.最终通过实现和对比，测试了我们的加速方法是有效且高效的.

本文中对于GEMM算法生成了较多的实现，并结合遍历的方法来进行自调优选择了最优的实现方法.但是仍旧存在着一些不足，采用遍历的方法相对较慢，没办法快速地找到效率最高的算法实现，有待进一步研究.

作者贡献声明：李茂文负责方法的设计与实验实现，以及文章整体架构设计、撰写和修改；曲国远负责全文结构设计与指导，以及各章节内容撰写；魏大洲负责数据的整理、校对和分析；贾海鹏负责部分设计的整理以及全文总结.