考虑微凸体相互作用的结合面静摩擦因数模型*

2022-06-08张学良许雍泰赵海路

组合机床与自动化加工技术 2022年5期

张学良，许雍泰，赵海路

(太原科技大学机械工程学院，太原 030024)

0 引言

机械系统中存在大量结合面，结合面的静态与动态特性影响着机械结构的性能，摩擦是结合面接触特性之一，对机械运转有着重要影响。摩擦会产生能量消耗与材料磨损，研究结合面摩擦对各种设备运转及社会生产有重要意义[1-2]。

国内外学者对结合面摩擦进行了深入研究，伴随着结合面研究的发展，人们开展了基于统计模型的结合面摩擦研究与基于分形模型结合面摩擦的研究。CHANG等[3]基于GW模型，通过研究弹性微凸体的切向载荷建立了金属结合面静摩擦因数统计模型。尤晋闽等[4]考虑微凸体弹性、弹塑性和塑性3种机制建立了结合面静摩因数统计模型。盛选禹等[5]基于分形接触理论，建立了结合面静摩擦因数预测模型。田红亮等[6-7]对分形理论进行改进提出了金属材料表面静摩擦因数分形模型并进行实验验证。张学良等[8]提出了与微凸体尺度等级关联的考虑微凸体完全弹性、第一弹塑性、第二弹塑性和完全塑性4种变形机制的结合面静摩擦因数三维分形模型。

上述研究对结合面静摩擦因数建模进行了一步步完善，但均未考虑微凸体相互作用对结合面摩擦产生的影响。结合面微凸体受到载荷作用接触面积发生变化，与相邻的微凸体逐渐产生挤压作用，使得真实接触面积与名义接触面积的比例逐渐增大，从微观上对结合面特性产生影响进一步表现为宏观现象[9]，故考虑微凸体相互作用分析结合面接触静摩擦因数更接近实际。CIAVARELLA等[10]在GW模型的基础之上考虑微凸体的相互作用后重新建立了接触载荷和变形的关系。ZHAO等[11]基于圣维南原理分析了微凸体相互作用对局部变形的影响。张伟等[12]建立了考虑微凸体基体变形和相互作用的结合面法向接触刚度统计模型。王润琼等[13]基于分形理论提出了考虑域扩展因子和微凸体相互作用的结合面接触刚度模型。这些模型揭示了微凸体相互作用对结合面特性的影响。

基于上述分析，本文将进一步考虑结合面微凸体相互作用的影响，研究建立与微凸体尺度等级关联的结合面静摩擦因数分形模型，并进行必要的仿真分析与实例验证。

1 考虑微凸体相互作用的微凸体接触力学模型

1.1 考虑微凸体相互作用的微凸体的法向载荷

本文采用与MB模型相同的假设，将结合面等效为一个理想光滑刚性平面和一个分形粗糙面的接触，尺度等级为n的微凸体变形前的轮廓曲线为[8]：

(1)

单个微凸体峰顶曲率半径为：

(2)

微凸体高度为：

(3)

微凸体相互作用示意图如图1所示[12]。

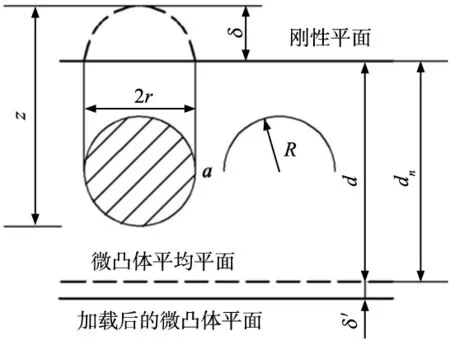
图1 微凸体相互作用示意图

图1中R为曲率半径；z为给定微凸体以平均平面为测量基准的轮廓高度数据；d为未加载时刚性平面与微凸体平均平面间距离；dn为刚性平面与结合面加载后微凸体平均平面的距离；r为微凸体的接触半径；a为接触面积；δ为系统总变形量，从图中可以得出：

δ=z-d

(4)

结合面接触过程中微凸体承受载荷，各微凸体之间产生相互作用，导致微凸体所在基底发生变形，综合表现为各微凸体的平均平面产生的向下位移δ′，由文献[13]可得：

(5)

式中，p为作用在微凸体上的平均载荷。

从图中可以得出微凸体实际变形量为：

ω=δ-δ′

(6)

考虑微凸体相互作用尺度等级为n的单个微凸体弹性阶段承受面积和载荷分别为[13]：

ane=πRnωn

(7)

(8)

将式(2)和式(4)联立可以得到弹性接触载荷与面积的关系：

(9)

由赫兹接触理论可知尺度等级为n的微凸体临界弹性接触变形量为[8]：

(10)

式中，K为硬度系数，与材料的泊松比v有关系，K=0.454+0.41v；E为等效弹性模量；H为较软材料的硬度。

当尺度等级为n的微凸体的变形量wn>wnec时，微凸体发生完全塑性接触变形，此时单个微凸体承受的法向接触载荷和接触面积为：

Fnp=K1σsanp

(11)

anp=2πRnωn

(12)

式中，K1=H/σs为较软材料的硬度与屈服强度之比。

1.2 考虑微凸体相互作用的微凸体的最大静摩擦力

结合面发生塑性变形的微凸体，由于局部的接触载荷已经使其发生塑性流动，将不能继续承受切向载荷，因此在计算静摩擦力时不包括已经发生塑性变形的微凸体，即没有达到弹性极限的微凸体能够承受切向载荷对摩擦力有贡献[5]。当切向载荷逐渐增大时，只有弹性变形的微凸体最终将达到屈服，此时的切向载荷就是最大静摩擦力，文献[5]中给出最大切向载荷即最大静摩擦力为：

(13)

本部分考虑微凸体相互作用计算分析了单个微凸体的法向载荷与最大静摩擦力，建立了考虑微凸体相互作用的微凸体接触力学模型。

2 考虑微凸体相互作用的结合面静摩擦因数模型

2.1 多尺度临界等级指数

结合面接触过程中尺度等级指数可根据微凸体变形量与临界变形量关系进行计算[14]，即ωn<ωnec。结合面弹性接触到塑性接触的临界等级指数如下：

(14)

2.2 微凸体接触面积密度分布函数

结合面接触微观上表现为多个微凸体接触，文献[19-20]给出了结合面中微凸体接触面积密度分布函数[13]：

(15)

式中，φ为域扩展因子，其表达式为：

(16)

为方便后续计算文献[16]假定式(15)为某一尺度等级下的微凸体接触面积密度分布函数，并引入系数Q来表示不同尺度等级微凸体接触面积密度分布函数：

(17)

(18)

式中，anl为尺度等级系数为n时微凸体最大接触面积；an为尺度等级系数为n时微凸体接触面积。

2.3 考虑微凸体相互作用的结合面法向接触载荷

结合面弹性接触法向载荷如下：

(19)

结合面塑性接触法向载荷如下：

(20)

结合面接触载荷：

F=Fre+Frp

(21)

2.4 考虑微凸体相互作用的结合面切向接触载荷

由第1.2节可知，结合面接触所承受的切向载荷即最大静摩擦力为：

(22)

2.5 考虑微凸体相互作用的结合面静摩擦因数模型

根据静摩擦因数的定义可得结合面静摩擦因数为：

(23)

为了计算结果具有通用性，此处进行如下无量纲化处理：

(24)

(25)

(26)

本部分考虑微凸体相互作用计算分析了结合面尺度关联法向载荷、最大静摩擦力和静摩擦因数，建立了考虑微凸体相互作用的结合面静摩擦因数尺度关联三维分形模型。

3 结合面静摩擦因数模型仿真分析

3.1 考虑微凸体相互作用的结合面静摩擦因数分析

本节选取不同分形维数，对结合面静摩擦因数与无量纲法向接触载荷进行考虑微凸体相互作用与不考虑微凸体相互作用对比分析。表1给出接触表面材料等效弹性模量E，GPa；等效硬度H，GPa；较软材料泊松比v，微凸体的尺度等级n取值范围[14]。

表1 等效结合面参数

将参数代入本文计算模型，进行数值仿真，结果如图2所示。模型1考虑了微凸体相互作用，模型2未考虑微凸体相互作用。考虑微凸体相互作用结合面静摩擦因数随着无量纲接触载荷增大而减小与文献[8]中静摩擦因数变化趋势一致。在数值上考虑微凸体相互作用时静摩擦因数相对较大，这是由于结合面同等参数条件下接触，微凸体相互作用导致结合面微凸体变形量或者接触面积减小，致使结合面接触过程处于弹性接触的微凸体所占比例增大，而弹性接触微凸体变形对静摩擦因数有主要贡献[8-12]，因此考虑微凸体之间相互作用时结合面静摩擦因数会增大。

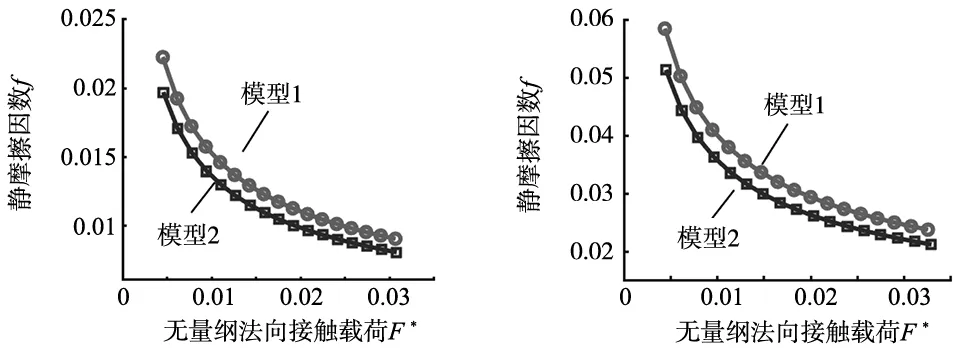
(a) D=2.1 (b) D=2.2

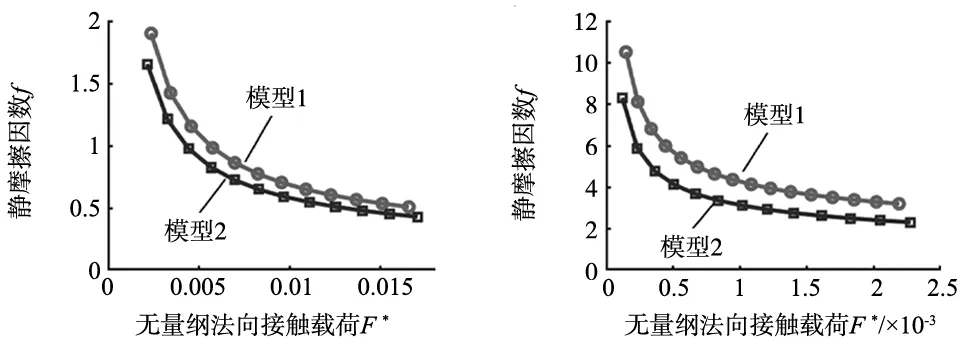
(e) D=2.5 (f) D=2.6

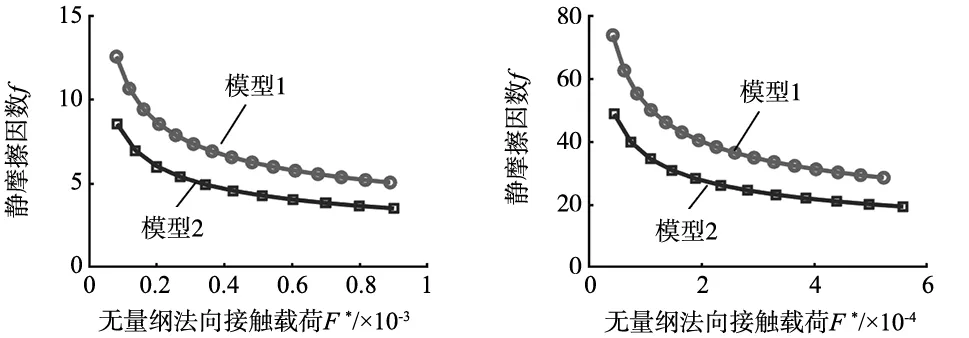
(g) D=2.7 (h) D=2.8

(i) D=2.9图2 静摩擦因数与无量纲法向载荷仿真分析

3.2 基于本文模型分析不同材料结合面静摩擦因数

本节采取文献[17]材料参数如表2所示，将三组结合面材料参数分别代入本文模型，如图对比分析了不同材料结合面静摩擦因数随着无量纲载荷的增大而减小，进一步将本文模型与实际结合。表2给出接触表面材料等效弹性模量E，GPa；等效硬度H，GPa；较软材料泊松比v。

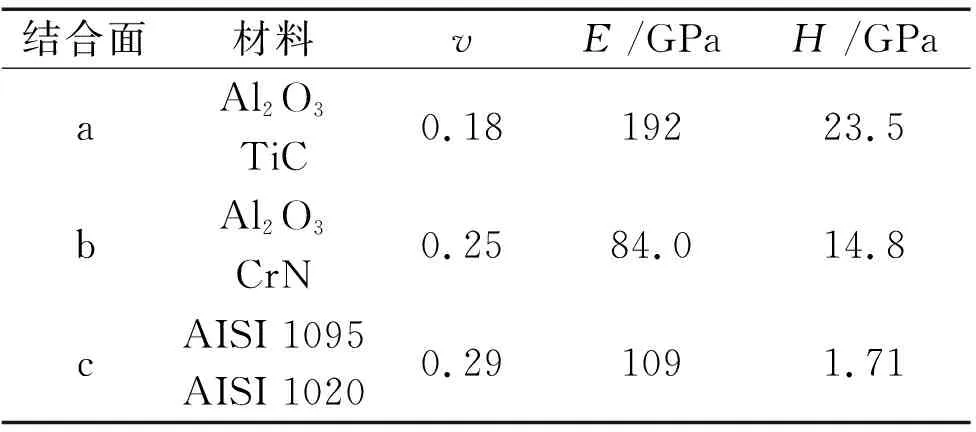
表2 结合面材料参数

图3中模型1考虑了微凸体相互作用，模型2为未考虑微凸体相互作用，仿真分析表明不同材料结合面接触摩擦在考虑微凸体相互作用的时候较大比不考虑时。对比结合面a、b和c仿真图像可以发现不同材料的结合面间微凸体相互作用对摩擦系数的影响不同，这是由于微凸体相互作用导致接触过程中弹性阶段微凸体所占比例的增大幅度不同，因此对静摩擦因数的影响也不同，图4对此采用塑性指数进行具体分析。

(a) 结合面a (b) 结合面b

图4取不同塑性指数φ对静摩擦因数与无量纲载荷关系进行了仿真分析，并在塑性指数相同时分别进行考虑有无微凸体相互作用对静摩擦因数的影响，模型1考虑了微凸体相互作用，模型2未考虑微凸体相互作用，图4中的图像分别对应结合面a、b和c的仿真分析。

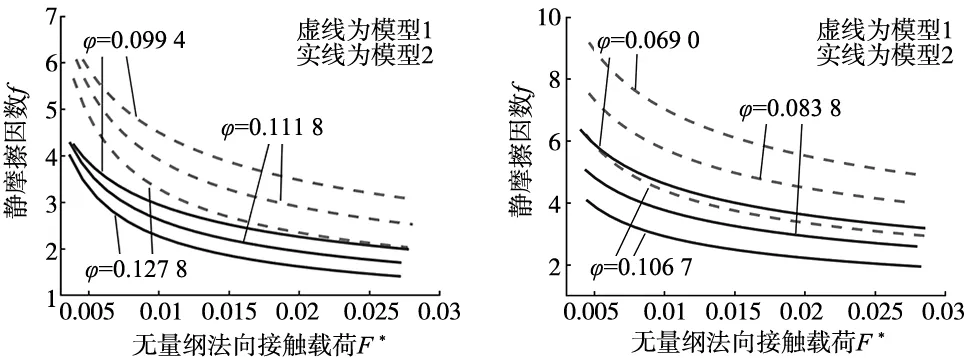
(a) 结合面a (b) 结合面b

图中微凸体相互作用对静摩擦因数的增大幅度随着塑性指数的减小而增大，塑性指数越小微凸体相互作用越明显，致使弹性微凸体所占比例增大，进一步导致静摩擦因数增大。图4中还可以发现随着塑性指数增大静摩擦因数减小，这是因为在同样的法向载荷条件下，塑性指数越大粗糙表面上的微凸体越易发生塑性变形，使得弹性状态的微凸体所占比例减小，进一步对静摩擦因数的贡献减小，这与文献[4]中相应的变化趋势一致[4-12]。

3.3 本文模型与实验数据对比

为进一步验证模型的正确性与合理性，本部分引用文献[8]和文献[18]的结合面参数与实验数据进行对比分析，三维粗糙表面分形维数和粗糙度分别为，D=2.218 5，G=6.891 3×10-5m，取样长度L=8.8 mm，微凸体等级指数为6～39，复合弹性模量E=59.52 GPa，较软材料硬度H=0.785 GPa，名义接触面积Aa=78.54 mm2。

图5为本文模型与实验数据的仿真结果，模型1为考虑微凸体相互作用时仿真图像，模型2为未考虑微凸体相互作用时的仿真图像，图5中对模型1模型2局部图像进行了放大处理。静摩擦因数伴随无量纲接触载荷增加而减小与实验数据变化趋势相同；取相同无量纲法向载荷，考虑微凸体相互作用时结合面的静摩擦因数更接近实验数据；进一步验证了本文方向的正确性。对图5中模型1与模型2曲线进行拟合，再求取静摩擦因数增长百分比如图6所示，纵坐标给出法向载荷相同时微凸体相互作用导致静摩擦因数增长百分比，进一步表明微凸体相互作用的重要性。

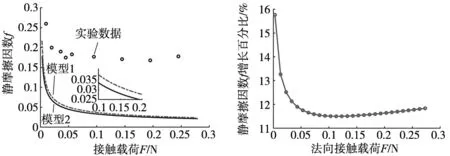
图5 仿真分析与实验对比图6 微凸体相互作用增幅百分比

由于本部分所采用的实验数据来源于考虑磁头磁盘界面摩擦简化实验模型，一般情况下承受较小载荷，所以图5中模型1、模型2图像二者摩擦因数数值相差较小。本文模型未考虑粘着力，由文献[18]知道粘着力会导致静摩擦系数增大，同时本文模型没有考虑弹塑性接触，因此本文模型所得静摩擦因数数值上与实验数据有一定差异。下一步继续研究微凸体相互作用及粘着力影响下弹塑性接触的静摩擦因数。