改进K-means聚类算法的自适应Canny算子工件边缘检测*
2022-06-08张宇廷王宗彦范浩东
张宇廷,王宗彦,王 曦,范浩东
(中北大学 a.机械工程学院;b.山西省起重机数字化工程技术研究中心,太原 030051)
0 引言
随着数字化信息时代的发展,基于图像处理分析的工业化智能检测技术日益成熟,数字化图像基本处理衍生出了大量的算法结合识别处理与自适应图像分析等方法[1]。包括Otsu算法的阈值处理,多形态学图像的开运算与闭运算,多目标优化算法图像处理都成为了当代数字图像处理的热点[2-4]。
其中,图像的首要识别特征为边缘轮廓的标定过程,应用的相关技术为图像分割与阈值处理[5]。传统的边缘检测算子包括LoG检测器,过零点检测器,Prewitt检测器,Sobel检测器与Canny边缘检测器。其中在简单工件识别方面,运用效果最佳的主要为Canny算子与Sobel算子[6]。其中王海龙等[7]通过改进Canny插值的方法自主选择合适阈值,对比了不同阈值下图像鉴别结果。张加朋等[8]在使用Canny算子检测工件时将高斯滤波改成了中值滤波,将高低梯度值与最大方差阈值结合,有效的避免了工件表面污渍带来的影响。黎浩等[9]运用顶帽变换的思路进行Canny-Otsu算法处理,实现了带钢工件的表面缺陷检测。但是在面临复杂相似工件的情况下,传统的Canny边缘检测与自适应Otsu阈值优化处理在面对锯齿与孔洞的时候可能产生锯齿边缘粘连,孔洞特征失效等情况[10]。
本文提出了一种改进K-means算法自适应Canny算子边缘处理技术,通过改进算法分割复杂工件图像得到不同的锯齿与孔洞特征,再进行形态学运算处理得到明显的图像特征,对比不同的聚类K值进行边缘的最优化处理,由于边缘轮廓复杂性在改进Canny算子方面进行梯度方向的增加,使用最小二乘法进行孔洞与锯齿拟合。
1 设计思路
传统的工件边缘识别思路为使用强大的Sobel与Canny算子嵌套模板,人工调整内核与模板,对于简单形状工件而言有较为良好的边缘处理效果,Canny算子与Otsu阈值优化的结合使得工件阈值分析更加合理,但是对于复杂工件而言,它所具有的一般特征为细小孔洞,非标准形状、锯齿、粗糙表面等特征都会为边缘标定造成困难。因此提出了一种改进K-means算法的Canny边缘检测方法,总体设计思路如图1所示。
本算法结合聚类算法与Canny边缘检测,着重考虑到锯齿、奇异边缘、细小孔洞等细节处理,相似工件图像不需要进行多次调整阈值与降噪,对于光源影响下的工件边缘,采用K-means聚类改进算法实现目标为阴影部分与背景重合,与前景目标区分,检测出的图像中细小孔洞面积与原有图像保持一致,锯齿特征不粘连失真,图2为测试工件类型。

图2 测试工件
对应的Canny算子也需要改进,由于边缘特征的复杂性除去原有水平与垂直梯度方向,添加45°与135°方向处理,引入K-means中的数据堆积特征值,最后对于多余边界进行形态学腐蚀操作,对比峰值信噪比(PSNR),结构相似性(SSIM),测试多组数据,选取平均检测结果。
2 K-means图像分割
2.1 K-means聚类算法简介
K-means聚类算法作为数据挖掘与图像信息处理中使用到的聚类为无监督式样本,它的基本思想规定固定数量k种聚类,每一种感兴趣区域(RoI)分配最近均值的聚类,反复迭代细化均值,得到为区域化块状连接图像[11]。不同于超像素的多区域分割思路,采用整体分割使得分割效率大大提高,K-means常用于数据神经网络处理与图像分析,有效的平滑细化图像特征点与边缘[12]。
2.2 自适应K-means算法改进
2.2.1 传统K-means图像分割
传统的K-means算法适用于边界纹理不复杂的图像边缘判定[13],而且在寻找区域平均像素值时可能由于噪声,分辨率,光源等外在因素的影响,众多噪声点和孤立点污染整个图像区域,因此改进K-means算法的主要目的是为了平滑不必要的细节框架,聚集必要的边缘特征。
由于聚类算法本身分割图像具有随机性,因此随机选取K值进行数据簇拥,对原始Canny边缘弱化的像素点进行图像分割。需要确定需要的K值大小。使用MATLAB2018a分析工件图像,取K=2~6的聚类样本作为参考图像。传统K-means图像分割如图3所示。

图3 传统K-means聚类分割
图3a为工件原始图像,图3b~图3e为K值为2~6的聚类分割结果,可以看出图3b丧失了基本边缘特征,图3d和图3e的工件存在明显的色差梯度变换与点噪声,会干扰后续的Canny边缘检测结果。
2.2.2 改进算法原理
针对传统K-means聚类算法的图像失真与固定K值不易输入分析的问题,建立相应的数学模型。基本思想为图像一般分为前景值与背景值,提取需要的轮廓信息。改进原始算法单一K值域的思想,分别取两种不同的K值区域规定K聚类的数量,样本集合分别为Q1、Q2。令Q1={z1,z2,…,zQ1},Q2={z1,z2,…,zQ2},将Q1,Q2分别划分为K个最优不相交簇,聚类簇C={C1,C2,…,Ck}。数据集合不相交公式为:
(1)
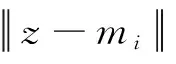
(2)
通过计算公式得到两个不同的K聚类均值mi1、mi2,K=[K1,K2],其中{K∈N2≤K≤6},随机进行数据聚集反复迭代。
mi+1=mi
(3)
直到没有产生新聚类变换为止,自动更新聚类值,拟合出最优背景与前景K值如图4所示。

图4 数据聚值拟合结果
将不同前景与背景的K聚类值进行拟合,但是不能将数据混叠造成图像干扰,随机排布K值矩阵[1,1][1,2]…[6,6],通过15组拟合数据得出最佳区域为随机K值聚类集合的并解,K∈[1.732,3.227],因此K的建议取值为2与3。
对得到的最优前景图像与背景图像进行小波融合分析,对于水平、垂直、对角方向的高频信息进行提取,图5为融合过程。改进后的图像的边缘轮廓与原图像分割明显,提取黑色像素通道即可提取工件基本轮廓。
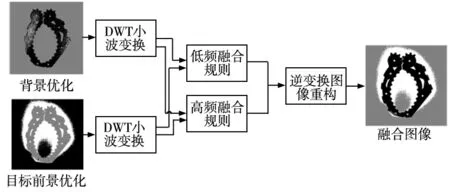
图5 融合示意图
2.2.3 算法验证
聚类相关分析使用MATLAB2018a进行仿真测试,测试样本为原先Cameraman图像对比传统K-means算法。图6所示为验证过程。
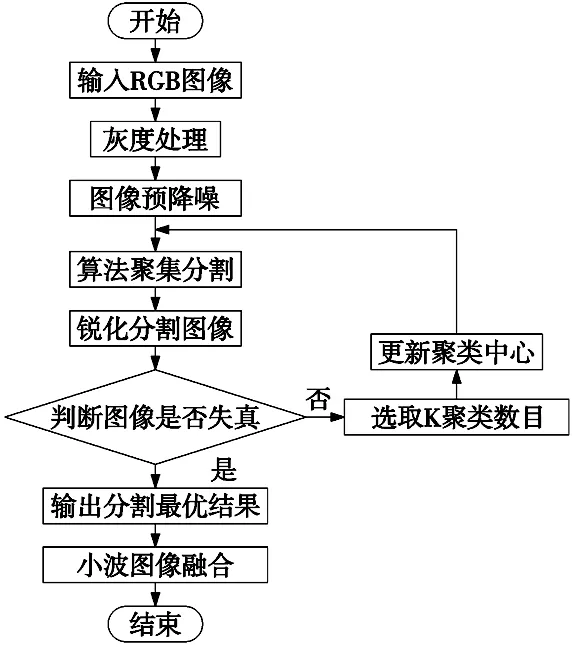
图6 具体验证过程
通过改进算法的实验验证,得到改进后的K=2~6聚类如图7所示。

图7 改进K-means聚类算法图像处理
与原算法对比图基本轮廓清晰可见,边缘未存在失真,图7b与图7c的背景缓和,工件像素梯度平滑,图7d与图7e虽然仍存在梯度变换,但对比原算法有了明显改进。该仿真证明该改进算法聚类K=2~6取值实现的可行性,其中图7a~图7c可用于后续的Canny边缘检测处理。
改进算法后的程序运行时间由于算法步骤的简化以及自动过滤异常值与偏态分布,运行效率大大提高,选取K值,运行20次取平均时间,测得优化前后时间如表1所示,优化时间明显缩短。
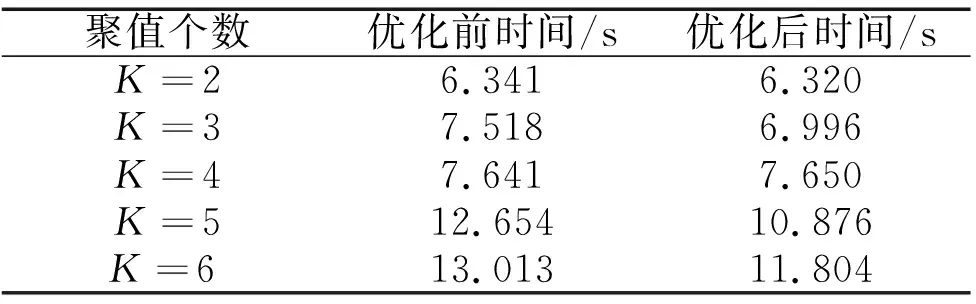
表1 优化前后运行时间对比
3 自适应边缘检测改进
3.1 改进Canny原理
Canny边缘检测器是Edge算法中较为突出的检测算法,检测的三项指标为低错误率,边缘定位点趋于真实,真实边缘点返回单响应点。本文所检测的工件还需要保证锯齿孔洞特征的相似性(SSIM)与高性能的峰值信噪比(PSNR)。
改进Canny检测的基本步骤如下:
(1)原始Canny图像进行Guass滤波,降低孤立点带来的影响,加入双边滤波,得到的图像边缘相似度会大大提高,提升峰值信噪比。Guass滤波与双边滤波相关函数为:
(4)
(5)
式中,σ、σs、σr为标准差,用于改善图像平滑度;i(x,y)为输入图像;i(m,n)为像素强度值,用于保持梯度。
(2)套用Sobel检测器检测图像的x轴与y轴梯度幅值与方向。实现横向与纵向的边缘数值估计。梯度幅值与方向公式为:
(6)
(7)
式中,iGS(x,y)为平滑后的图像,由于需要检测锯齿与孔洞,需要添加45°与135°方向模板。梯度模板为:
(8)
梯度幅值公式演变为:
(9)
式中,G45°、G135°为梯度卷积后的方向梯度幅值。
(3)对于梯度图像在局部极大值包含宽脊进行非极大值抑制操作,规定了相关的梯度向量∝(x,y)。
(4)在进行滞后阈值过程中,使用低阈值TL与高阈值TH检测边缘,通过全局阈值优化,再进行连通性分析连接图像相关真实点。最终得到完整检测结果。
3.2 优化边缘对照
将上述原理输入到MATLAB与OpenCV实现相关边缘功能,将处理好的聚类图像进行二次优化处理,如图8所示。

(a) 阈值分割 (b) 非极大值抑制图8 Canny优化过程
最终融合K-means的数据堆积,如图9所示。
图9 数据堆叠过程
得到最终边缘检测结果,与Sobel检测,传统Canny检测,Prewitt检测,阈值优化Canny检测对比,结果如图10所示。
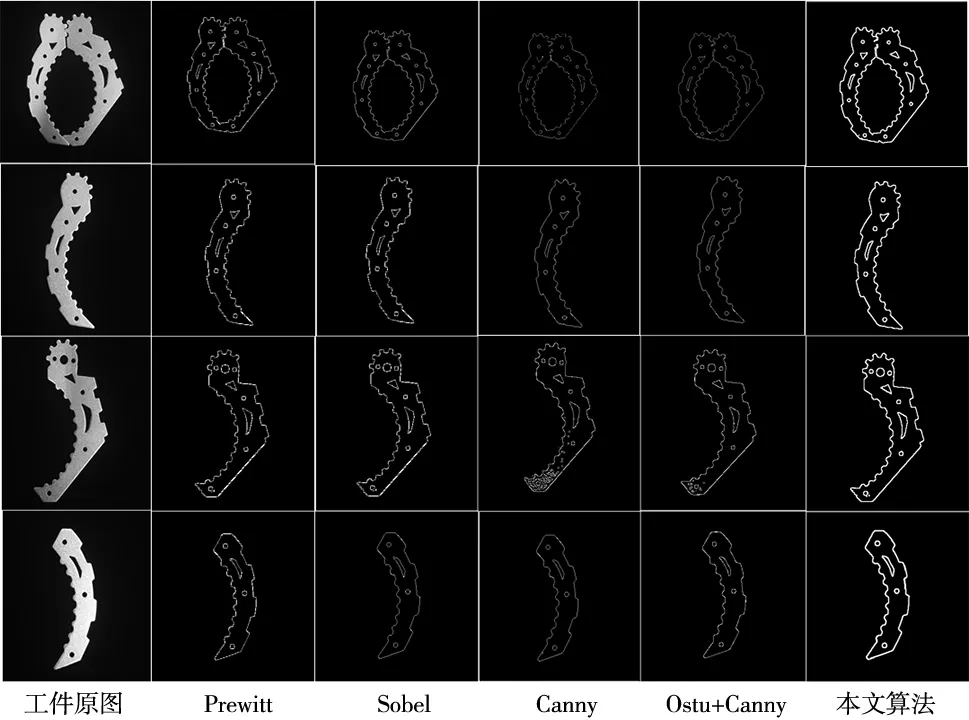
图10 边缘检测结果
每种算子运行20次取最佳边缘验证结果,Prewitt检测算子噪声点很少,但是目标与背景混杂,未能有效检测边缘,传统Canny搜寻边缘特征过多,Sobel算子背景边缘处理不明显,Canny+Otsu在阈值分析过程中大量边界缺失。而本文提出算法则有明显边缘特征,且噪声去除效果明显。
4 实验与结果分析
4.1 实验准备
验证出改进K-means算法的边缘检测可靠性后,进行相关的工件检测实验,由于不同计算机处理算法具有差异性,所用设备搭建处理环境统一为图11所示平台,选取不同带有细小孔洞与锯齿特征的奇异非标准工件作为参考。

图11 实验平台
搭建的硬件框架主要分为光源、摄像头,待测工件以及测控电脑组成。采用LED光源负责工件与黑色背景的对比处理,减少阴影造成的影响。采集图像的摄像头型号为MV-CA013-20GM,固定在水平框架上,其分辨率为1280×1024,开启曝光模式增加背景与目标工件对比度。测控电脑环境为AMD R5-4600H四核16 G内存,进行实时图像处理。
软件准备为测控电脑搭载Visual Studio2019与OpenCV3.4.6进行图像预处理,使用MATLAB进行算法优化与数据拟合,GigE Vision用于电脑与摄像头的协议连接。
4.2 孔洞失真处理
检测带有细小孔洞的工件不仅需要使处理后的工件边缘基本完好问题,还需要保证形状保持一致,在算法处理数据堆积的过程中,由于上述三种工件的基本孔洞特征直径在1.5~2.3 mm之间,可能造成形状的失真细小圆孔变成矩形孔洞,会影响到相似度评价(SSIM)与测量尺寸,因此需要使用最小二乘法拟合工件圆孔,具体原理如下:
首先进行相关数学模型搭建,设圆心为(A,B),半径为R,平面圆形一般方程为:
x2+y2+ax+by+c=0
(10)
式中,a=-2A;b=-2B;c=A2+B2+C2,测试i组不同数据簇(xm,ym),m=1,2,…,i,算出目标函数为:
(11)
对a,b,c同时偏导,令F=0,得到相关矩阵为式(12),通过解得a,b,c计算拟合圆相关参数:

(12)
通过解得a,b,c计算拟合圆相关参数。随后进行微面积筛选与孔洞特征圆形拟合,通过OpenCV得到细化图像轮廓,如图12所示。
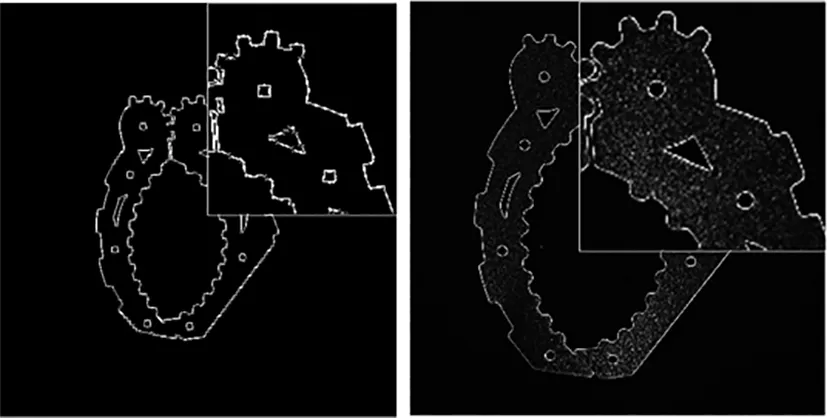
图12 圆形孔洞拟合对比图
4.3 结果与分析
对改进K-means算法进行实际验证,采集到的图像为工件1,2,3,采集30组数据共120张,评价标准为:
(1)对三种工件进行相似度(SSIM),峰值信噪比(PSNR)的一般评估,观察所测工件不同算子条件下的数值对比,将30组图像数据进行平均计算,得到可靠的一般评估与Canny检测和Otsu+Canny检测对比。
(2)由于工件的特殊性,需要对锯齿形状与孔洞进行评判,评判标准为锯齿与圆形孔洞的失真程度。
选取传统Canny算子,基于Otsu的Canny算子作为对照,添加均值为0.2,方差为0.05的高斯噪声,放大特征细节得到边缘轮廓如图13所示。
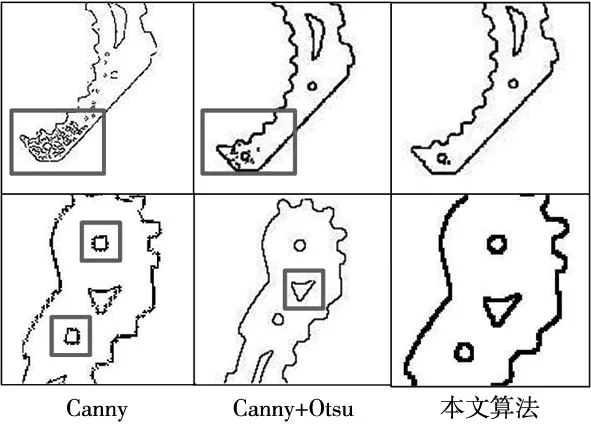
图13 细节对比
由图可知,Canny算子的边缘不连贯,且缺失孔洞与锯齿特征,基于阈值优化的Canny算子虽然可以基本检测边缘轮廓,但孔洞边缘存在不连贯,部分锯齿失真。而本文算法去噪能力强,孔洞与锯齿拟合程度高,具有很强的鲁棒适应性,边缘平滑度更高。
取30组实验数据平均值,对比工件图像的相关相似度与峰值信噪比,如表2所示。细小孔洞与锯齿特征检测结果如表3所示。

表2 图像评价对比表

表3 孔洞锯齿特征统计 (个)
由表2可以看出本文的改进算法的峰值信噪比和结构相似度较传统Canny算法与阈值优化后的Canny算法而言明显提高,验证了改进算法的可靠性。由表3可得基于改进算法的Canny边缘检测的孔洞锯齿识别率有所提高, 特征与边缘细化比原有算子更为平滑。
5 结论
通过改进K-means聚类算法实现自适应的Canny边缘检测过程,首先进行复杂工件图像预处理操作,然后通过改进K-means算法实现区域工件图像的梯度优化,配合Canny检测算子进行细小孔洞与锯齿处理,最终得到优化的边缘检测结果。
处理后的图像不仅可用于机器视觉的标定检测,而且得出的边缘提取效果较传统Canny边缘检测在相似度与峰值信噪比评价上有所提高,在孔洞与锯齿边缘对比上失真程度下降,验证了改进K-means算法在Canny边缘处理上的可行性。
