基于非线性TD滤波的PLC灌装系统研究*

陈 湘，张 泽

(贵州大学机械工程学院，贵阳 550025)

0 引言

目前，液体灌装设备在市面上种类较多，但大部分设备其结构复杂，占地面积大[1]，出于产量和成本考虑，小微企业引进成套的自动灌装设备并不合理。因此，高效可靠的低成本灌装具有较广阔的市场空间。

要实现高效可靠的灌装，其控制系统必须稳定可靠。控制系统可靠性主要体现在其接收和产生信号过程的精确性和信号处理的实时性等方面[2-3]。电压反馈的信号极易受到环境噪声干扰，会极大影响接收信号的准确性，导致控制质量下降。因此，对采集信号的滤波是不可忽视的问题。滤波器的实现方式可以是由硬件线路构成的模拟滤波，比如典型的 RC 电路，或者由特定程序构成的数字滤波，比如频率筛选器[4]。模拟滤波需要额外硬件电路设计，且滤波参数不容易调整。因此，在不增加系统复杂度的情况下，数字滤波器是普遍适用的方法。传统的低通滤波器能够去除高频噪声问题[5]，但在模型不确定时，很难找到合适的滤波因子，没有普遍性，滤波后信号会引入一定的超调量，并且曲线平滑性较差，在灌装系统中会极大影响灌装精度，因此需要引入通用性好、无超调、平滑性好的滤波器。

跟踪微分器(tracking differentiator,TD)采用最速控制函数，能快速跟踪输入信号，时延低，并从污染信号中提取微分信号，不引入外部模型，这使得TD参数易于调节，并且TD可以抑制自身超调，大幅提高控制精度[6-7]。

在灌装系统中，所用控制器多为可编程逻辑控制器(programmable logic controer,PLC)[8]，因此，为提升PLC灌装系统的灌装采样精度，实验将非线性TD算法与PLC相结合，通过TD算法提高PLC在高干扰环境下的采集精度，从而改进设备性能，实现精确控制目标。

1 TD滤波算法

PLC的模拟量采集自带一定的滤波性能，但有一定局限性，无法自由更换算法。因此，本文在选取适合灌装过程抗电信号及液滴波动等干扰的滤波算法的基础上，以PLC基本程序结构为基础，来实现相关滤波过程，提高灌装的可靠性和精度。

1.1 滤波器的选择与参数确定

工厂现场环境比较复杂，采用的称重传感器大多是模拟量输出，测量数据会受到电磁干扰而引入电噪声，进而影响到灌装控制的精度。解决输入噪声可以从改变现场电磁环境和增加滤波两个方面着手。考虑到工厂环境和灌装过程相对固定，有效信号频率范围较低，能比较合理的区分实际信号和噪声干扰，因此本文采用滤波的方式实现准确的数据采集。

由实测数据可知(如实验验证部分图11、图12所示)，本文需要解决高频电噪声带来的干扰问题，可以设计TD滤波器来解决。

非线性TD的一般形式如式(1)所示[9]：

(1)

式中，r为跟踪因子；v0(t)为输入信号。

由于控制系统大多为离散采样，通常我们考察非线性TD的离散形式[10]：

(2)

式中，fhan(x1,x2,r,h)为离散系统的最速控制综合函数，其算法如式(3)所示。

(3)

式中，为了消除速度曲线中的超调现象，抑制微分信号中噪声放大，通常把fhan(x1,x2,r,h)中h的改为与步长h独立的新变量h0，且取h0大于步长h。

1.2 跟踪微分器的优化

PLC是离散采样控制系统，满足上述的非线性TD离散形式。由于离散系统的最速控制综合函数较为复杂，其算法结构在PLC中不易实现，会重复使用较多运算模块，加长PLC的扫描周期，不利于内存中其他程序执行。在此基础上，需要优化上述非线性TD算法[11]。

在灌装场景中，灌装的模拟量值由零到设定值，相对而言，滤波后的x1值不小于零。根据快速最终函数推导过程中，点a±i，i≥2，位于两个半条抛物线上：

(4)

(5)

式(4)为a+i所在曲线，式(5)为a-i所在曲线，根据场景条件x1≥0，故k步内能到达原点的初始点[x1,x2]应在k-等时区的右下部分，在不考虑零点波动的情况下，可近似的认为式(6)成立。

sign(x2)=-sign(y)=-1

(6)

去掉条件语句，利用符号函数可将式(3)改写为式(7)：

(7)

2 PLC程序实现

控制系统使用三菱FX系列的FX-3GE-24M PLC作为控制器，使用GX -Work2进行PLC结构化梯形图(FBD)编程，使用FBD编程可以自定义函数，对算法实现中有着重要作用，结构清晰，利于优化设计。

算法结构中有着大量sign函数计算、比较计算，直接构建语句指令时，会造成内存资源浪费，使其结构冗长，不便于阅读。因此，将sign函数、绝对值函数以及TD滤波函数分块书写，定义成子程序函数，方便调用。sign函数、绝对值函数用PLC方法实现如图1和图2所示。

图1 sign函数PLC实现图 图2 绝对值函数PLC实现图

2.1 滤波程序PLC优化实现

PLC采样是周期循环过程，每次滤波所消耗时间都会通过周期循环叠加到主程序循环上，当采样频率较高时，此滤波所需的时间成本就会过高，会导致主循环中其他程序无法正常执行，因此，在使用PLC搭建TD函数时，需优化其算法结构，减少TD滤波的时间成本。

与式(7)对比，根据环境条件x1≥0，主要对以下的两个表达式进行了优化：

(8)

(9)

PLC的扫描周期主要包含输入采样、程序处理、输出刷新，以及自诊断及与外设通信等时间。因此，扫描周期长短是判定程序是否精简的标准，三菱FX系列中的特殊功能寄存器D8012存放着当前最大扫描周期，根据测试，PLC无执行程序时的扫描周期为0.9 ms。

图3 无执行程序PLC扫描周期测量图

将式(8)、式(9)用PLC方法实现，如图4所示。

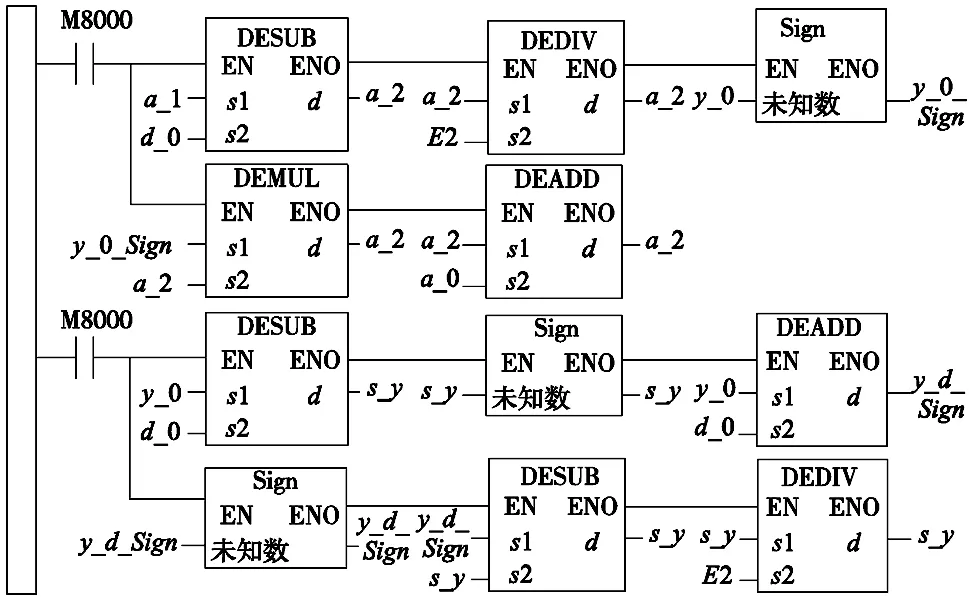
图4 原算法部分梯形图

PLC程序扫描顺序为由左至右、由上至下，图中程序严格按照公式的执行顺序设计，由图4中第一、二行可知，a_1(对应a1)减去d_0(对应d)，所得结果除以2，将计算中间值暂存于寄存器a_2中，y_0(对应y)通过sign函数计算，所得结果与寄存器a_2中值相乘，所得结果加上a_1，最终得到a2的值，三、四行同理，最终得到sy的值。在计算过程中，由于计算结果会下一个扫描周期刷新，因此将计算数值暂存在同一个寄存器a_2(FBD编程寄存器由用户定义)中，这样可使计算逻辑性清晰，并节约寄存器空间。

同时在PLC监测程序中得到每个扫描周期为1.9 ms，故TD滤波程序的时间成本为1 ms。

图5 原算法PLC扫描周期测量图

优化式(8)、式(9)后的表达式为：

(10)

(11)

将式(10)、式(11)用PLC方法实现如图6所示。

图6 优化算法部分梯形图

同时在PLC监测程序中得到每个扫描周期为1.7 ms，故TD滤波程序的时间成本为0.8 ms。扫描周期测量语句如图7所示。

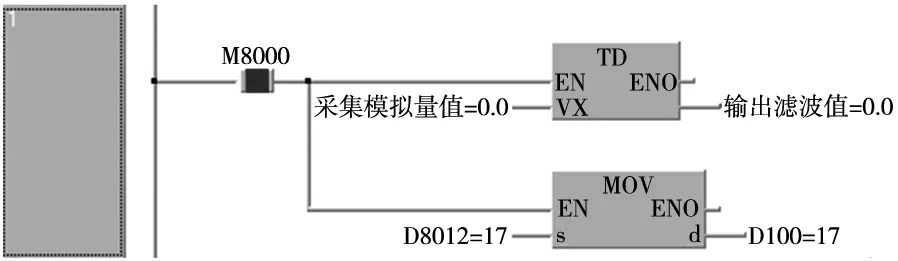
图7 优化算法PLC扫描周期测量

通过对跟踪微分器进行优化，成功将TD滤波的时间成本从1 ms减为0.8 ms，降低了滤波程序对主程序的执行时间占比。

2.2 PLC滤波中断程序

要达到好的滤波效果，采样周期的准确性需要保证，由于主程序根据使用条件、场景不同，其复杂程度也存在较大差异，PLC的扫描周期不定，因此，在采样过程中，需要将滤波程序放入中断中，用内部定时器控制其采样频率，可保证采样频率的稳定性，使滤波达到较好的效果。

为了不引入其他脉冲设备，增加系统复杂性，实验使用PLC内部定时器进行中断设定，设定中断事件为I610，其中的10代表设定中断时间为10 ms，PLC对反馈模拟信号的采样频率为10 ms。

每次进行中断程序，都会对x1、x2进行迭代运算，实现滤波目的，其中x1为滤波后的值，x2为噪声的微分，程序段如图8所示。

图8 中断程序PLC梯形图

图8第一行中，x_2(对应x2)乘以h_1(对应h1)，得到的值加上x_1(对应x1)，得到了新的x_1，完成x1的迭代运算；第二行为TD滤波运算，得到采样信号的近微分信号，INC程序块记录中断次数；第三行中近微分信号乘以h_1，得到的值加上x_2，得到新的x_2，完成x2的迭代运算。

3 实验验证

3.1 灌装实验平台搭建

灌装机系统控制结构如图9所示。PLC负责处理用户指令(开关量)和传感器的反馈(模拟量)，同时给出控制指令(开关量)用于控制过程和调速指令(模拟量)用于调整泵的工作实现精确灌装。控制的基本思路是，灌装设置由按钮开关转换为开关量输入PLC作为控制期望，压力传感器测量当前的灌装质量并由模拟端子采集反馈到PLC中，PLC中运行PID反馈程序，生成模拟电压信号输出到调速驱动器，驱动灌装泵工作，完成定量灌装。

验证基于所设计出的灌装实验平台，如图10所示，主要包括模拟滤波和灌装精度两个验证内容。

图9 控制结果及信号流程图 图10 灌装机实物及测试实验图

3.2 滤波程序实验验证

为了验证所设计滤波器的正确性，在进行灌装实验测试之前，先进行了滤波效果实验验证。手动倒入水进行定量称量，即在压力传感器上按实际速度加入4 kg水模拟灌装，并存储滤波前后两组数据来说明效果。

首先通过MX component建立一个PLC到PC的数据通道，同时使用MX sheet在EXCEL中创建Cell Area，PLC采集到的模拟量进行TD滤波，通过MX component建立的数据通道将滤波前后数据传输到EXCEL中进行记录[12]，数据的传输间隔为0.01 s。

在PLC中，为了能快速追踪采集信号，设定跟踪因子r为500，采样频率h为10 ms，综合函数中h0为100 ms。

同时为了说明优化TD算法的优势，在PLC中设计低通滤波算法，并进行了滤波实验。

实验结果如图11和图12所示，有如下几点结论：

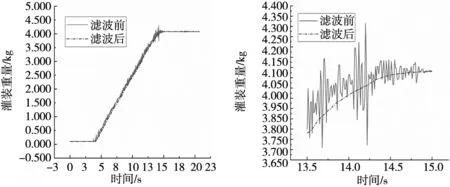
(a) TD滤波前后信号图 (b) 信号转折处细节放大图图11 TD滤波测试实验结果图

(a) RC滤波前后信号图 (b) 信号转折处细节放大图图12 RC滤波测试实验结果图

(1)滤波前信号毛刺较多，RC滤波能削减噪声幅值，但信号的平滑性较差；

(2)TD滤波后的信号平滑性好，曲线非常光滑，滤波前后信号峰峰值由0.15 kg降到0.002 kg以内，有效的提高了精度；

(3)RC滤波后信号有明显信号超调，影响灌装精度；

(4)TD滤波后响应基本和原有效信号一致，滤波没有造成明显的信号延时和超调。

以上结论表明TD滤波在灌装滤波中有较大优势，滤波效果好，有效提高了采集精度，为精确灌装提供了基础。

3.3 灌装精度测试

本文在压力传感反馈调速控制模式(实验一)的基础上，增加了采用TD滤波的反馈调速控制模式(实验二)，采用两种方式进行多次4 kg水的定量灌装，以最终误差为考量指标，来验证基于称重模拟量反馈的控制精度。

图13 灌装实验流程图

测试结果如表1所示，两个实验组的平均相对误差为分别为0.166%和0.871%，实验二的灌装精度明显优于实验一。结果表明，所设计的TD滤波器有效的提高了灌装精度。

表1 灌装实验结果

4 结束语

尽管目前PLC采集滤波技术也很成熟，但低端PLC自身并不具备实现的硬件基础，并且大多没有自带滤波模块，缺乏合适的滤波方法。对此本文针对低成本灌装，采用FX-3GE-24M PLC作为主控制器，设计了非线性TD的滤波算法，并对算法优化设计，使其更兼容低端PLC，有效提高了灌装精度。同时搭建了简易灌装实验平台，对所设计滤波算法进行了实验验证。

通过对比实验说明了算法优势，并验证了所设计滤波器的有效性，实验测试中滤波前后信号峰峰值由0.15 kg降到0.002 kg以内。实验平台4 kg液体灌装测试，平均相对误差为0.166%，满足企业对灌装精度的要求。后期的工作准备从算法的优化方式上切入，解决算法只适用于无负值信号处理的局限性，并简化算法结构使其适用于PLC程序。