多场耦合下三螺杆泵转子振动特性研究

2022-06-08陈小怡洪震

化工设备与管道 2022年1期

陈小怡，洪震

（泸州职业技术学院智能制造与汽车工程学院，四川泸州 646000）

三螺杆泵因其具有良好的吸入性能、流量均匀连续、振动小、噪声低等诸多特点，是应用十分广泛的一种容积泵，主要应用于石油化工产品等方面[1-3]。三螺杆泵由主动、从动螺杆组成，工作过程中由减速器带动主动螺杆，通过与从动螺杆转子啮合实现液体的吸入和排放，主从动螺杆转子结构性能的好坏直接影响到螺杆泵的工作效率和使用寿命[4-6]。

国内外学者对泵类产品作了相关研究，文献 [7]以全金属单螺杆泵为研究对象，通过实验在输送单相介质和气液两相介质工况下，研究分析了其特性曲线及内部压力的分布情况，结果表明，当输送单相介质时，全金属单螺杆泵的容积效率正比于转子转速。文献 [8]对三头单螺杆泵的螺杆转子进行研究，得到了螺杆泵定子的橡胶轮廓变形与材料的泊松比成正比的关系。文献 [9]对单螺杆泵的排液特性进行分析，得到螺杆泵的排液体积随偏心距呈反比，随密封盘半径成正比。文献 [10]基于计算流体力学方法，建立了单螺杆泵三维流场数值模拟计算模型，通过pumplinx 软件对不同气体质量分数、粘度和转速工况下单螺杆泵流场压力及速度分布规律进行了分析，得到了在不同气体质量分数工况下，含气率越高，螺杆泵流体域密封压力分布就会越低，流场内流体速度有所下降，下降幅度较小。文献[11]对单螺杆泵进行动力学研究，结果表明单螺杆泵定子的内表面由于转子的转动容易发生疲劳破坏。文献 [12]根据单螺杆泵型线方程建立采油螺杆泵的三维有限元分析模型，对包含热力耦合和流固耦合的多物理场耦合作用下的单螺杆泵刚柔螺旋曲面进行分析研究，探究了过盈量、转速、损耗因子和摩擦系数对定子生热的影响，但是对其耦合分析时采用的是二维模型数值模拟，因此具有一定的局限性。文献 [13]通过传热理论对单螺杆泵的橡胶衬套进行热力耦合分析，结果表明衬套的最大变形和最大应力与转速成正比。文献[14]通过有限元分析法分析了三螺杆泵螺杆与轴套间隙、螺杆转速以及进出口压差对螺杆泵流场压力和流速的影响，研究表明啮合区的流体较为复杂，齿槽间流体较为平稳。文献[15]基于有限元理论对三螺杆泵进行静力学分析，得到了螺杆转子的变形和应力从进口到出口逐渐增大。文献[16]研究三螺杆泵流场参数对螺杆转子结构变形和应力的影响，但未考虑三螺杆泵温度对转子强度的影响。文献[17]通过对三螺杆泵的使用寿命进行研究，设计出求解公式，研究者根据这一公式大大地缩短了螺杆泵的设计周期。

现阶段在三螺杆泵方面的研究较为欠缺，主从动螺杆转子的性能对螺杆泵的采油效率有很大影响，而三螺杆泵工作过程中的复杂环境，泵内的高温高压载荷引起螺杆转子产生变形和应力，破坏螺杆转子结构，直接影响到螺杆泵的工作效率。因此通过数值模拟方法研究螺杆泵流场对螺杆转子结构的影响有重要意义[18]。

1 计算方法

本文通过有限体积法求解螺杆泵工作过程中产生的压力载荷和温度载荷，基于CFD/CSD（Computational Fluid Dynamics/Computational structural dynamics）技术将压力载荷和温度载荷加载到主从动螺杆转子结构网格上，求解转子的结构方程得到转子的位移场，然后分析转子的振动特性，如图1 所示。

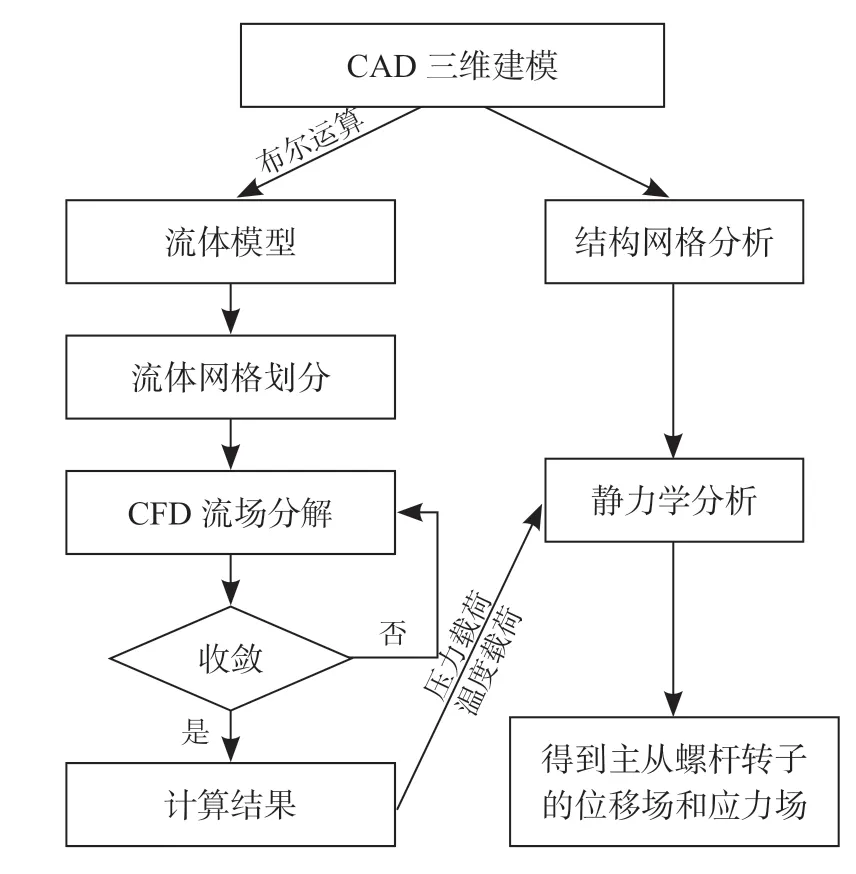
图1 计算流程Fig.1 Calculation process

三螺杆泵工作中一般输送高黏度原油，为准确模拟其内部流场，对计算中的流体进行假设：流体为不可压缩的非牛顿流体且是湍流流动，其基本方程为 [19]：

式中U——速度矢量；

p——流体压力；

μ——流体的动力黏度；

cp——流体的比热容；

ρ——流体密度；

λ——导热系数；

F——作用在流体上的质量力；

q——流体所吸收的热量；

T——流体温度；

φ——能量耗散函数。

螺杆泵流体与固体传递数据时应满足位移、应力、热流量、温度等守恒，即[20]：

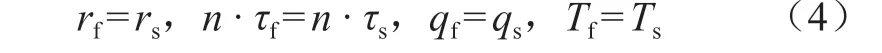
式中f——螺杆泵流场；

s——结构场。

本文将流场得到压力载荷和热分析得到的温度载荷作为转子的外载荷，其结构动力学方程为：

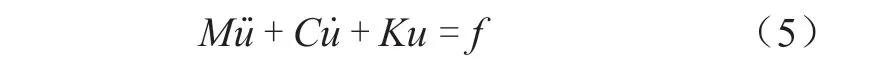
式中M——结构的质量矩阵；

C——结构的阻尼矩阵；

K——结构的刚度矩阵；

u——结构的位移矢量；

f——结构的外部载荷。

忽略结构变形和加速度对系统的影响，结构动力学方程简化为：

求解即可得到结构的位移场以及应力分布。

通过静态分析的应力位移向量u得到预应力效应矩阵S，考虑预应力效应矩阵S的影响，原来的模态分析方程可以简化为：

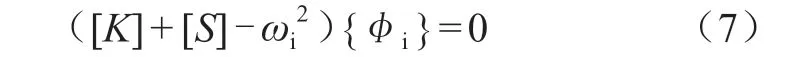
即可得到结构的振动特征方程为：

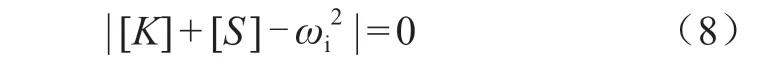
φi——相应的特征向量，即模态振型。

2 计算模型

本文三螺杆转子的几何数据根据文献 [21]建立，对三螺杆泵进行网格划分时，由于转子结构较为复杂，为了提高内流场和主从螺杆转子的网格质量，通过非结构四面体网格进行划分，得到三螺杆泵内流场和主从转子的计算模型如图2 所示，流场网格362 万个节点，245 万个单元，结构网格142 万个节点，98万个单元。

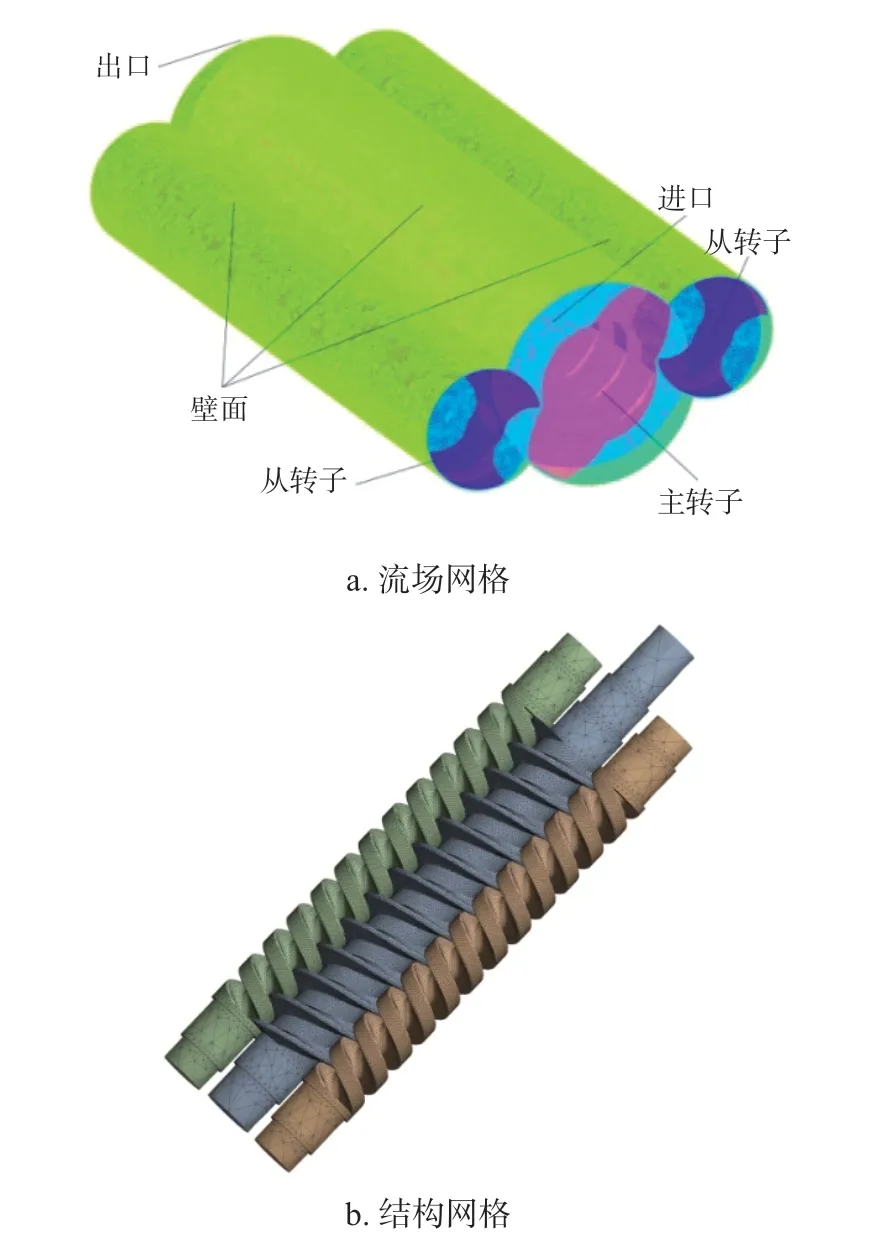
图2 计算模型Fig.2 Calculation model

3 方法验证

根据文献中给出的流场边界条件，螺杆泵的进口设置为压力进口，压力大小是标准大气压，出口设置为压力出口，压力大小设置为2 ～ 6 MPa，螺杆转子的转速为450 r/min，湍流模型为RealizableK-ε模型。通过监测三螺杆泵的输出流量和文献 [19]中的实验数据进行对比，如图3 所示。

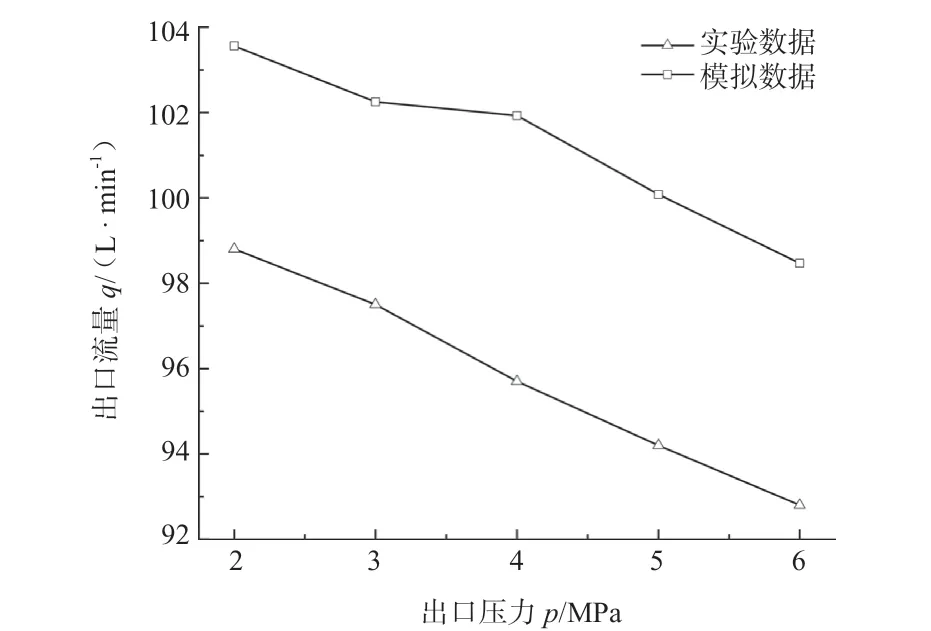
图3 计算数据与实验数据对比Fig.3 Comparison of calculated data and experimental data

从图3 可知，通过本文采用的数值模拟方法得到的计算结果与实验结果的误差在7%以内，且随着出口压力的增大，数值模拟值与实验值变化规律相符，说明该方法可用于求解三螺杆泵的内流场。

3.1 求解设置

在确定流场求解方法正确的基础上，对其进行耦合求解，螺杆泵采用46 号液压油，密度ρ= 890 kg/ m3，热导率0.12 W/ （m·K），比热容为189 J/ （kg·K），动力黏度μ= 0.46 Pa·s，考虑到三螺杆泵的实际工况，将螺杆泵的进口设置为压力进口，出口设置为压力出口，主从螺杆转子的壁面设置为旋转壁面，流体控制方程采用双方程RealizableK-ε模型，通过SIMPLEC 算法进行求解。通过数值插值技术将得到的压力载荷和温度载荷加载到螺杆转子的结构网格上，对转子结构求解时，螺杆转子的材料40Cr，其密度ρ= 7 850 kg/m3，泊松比为0.3，弹性模型E= 210 GPa，对流换热系数取548 W/（m2·℃），环境温度取25 ℃。

4 结果分析

4.1 温度载荷和压力载荷求解与加载

图4a 和4b 是三螺杆泵在出口压力为4 MPa 下产生的温度载荷和压力载荷，从图中可以看出，螺杆泵的温度载荷分布主要是靠近出口温度最高，然后向进口位置进行扩散，螺杆泵的压力载荷分布主要呈阶梯型，转子的出口压力最大，压力逐步向进口递减，形成温度载荷和压力载荷分布的原因主要是因为主从螺杆转子通过啮合挤压导致原油内能增大，温度升高，压力增大。

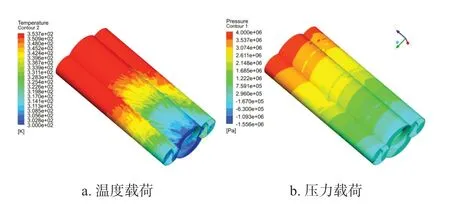
图4 三螺杆泵流场求解结果Fig.4 The solution results of the flow field of the three-screw pump

图5a 和5b 是将三螺杆泵产生的温度载荷和压力载荷加载到螺杆转子的结构网格上，从图中可以看出，螺杆转子上的温度分布以及液体压力分布与温度载荷和压力载荷的分布趋势相同，能够较为真实地反映出转子的受载情况。

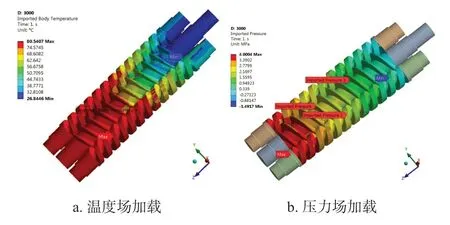
图5 主从动转子受载Fig.5 Load on the main and driven rotor

4.2 流热固耦合求解

图6 是三螺杆泵在出口压力为4 MPa 下的变形云图，图6a 是螺杆转子在扭矩作用下的变形云图，最大变形集中在阳转子与减速器相连接的末端，最大变形量达到0.019 6 mm，图6b 是主从螺杆转子在流固耦合下转子的变形云图，最大变形出现在从动螺杆的两侧，最大变形达到了0.051 mm，是扭矩作用下的2.6 倍。c）图是螺杆泵在热固耦合下转子的变形云图，最大变形在螺杆转子的进口位置产生，主要是因为转子在工作过程中受热膨胀产生较大的变形，另一方面是因为该位置主螺杆与减速器相连，产生较大的变形，最大变形达到0.211 mm，是流固耦合下的4 倍左右。d）图是螺杆泵在流热固耦合下转子的变形云图，综合考虑螺杆泵产生的温度载荷和压力载荷对转子的影响，从图中可以看出，转子的变形分布趋势与转子在热固耦合下的趋势相同，说明转子的变形主要是由螺杆泵产生的温度载荷引起的，最大变形量达到了0.235 mm，相比热固耦合下的最大变形，增大了11%。

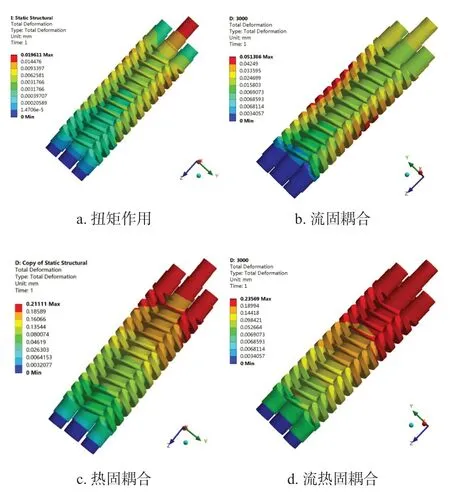
图6 螺杆转子的变形云图Fig.6 Deformation cloud diagram of screw rotor

图7 是螺杆泵在出口压力为4 MPa 下的应力云图，图7a 是主从螺杆转子在扭矩作用下的应力云图，从图中可以看出螺杆转子的应力主要集中在主动转子上，最大应力达到74.032 MPa。图7b 是螺杆转子在流固耦合下的应力云图，可以看出，主从螺杆转子的齿根位置产生交的应力集中，最大应力达到了237.73 MPa，是扭矩作用下的3.2 倍。图7c 是螺杆转子在热固耦合下的应力云图，主从螺杆转子的齿根产生较大的应力集中，螺杆转子位于出口位置的轴端产生较大的应力，由于温度场作用于转子后转子只能沿Z轴的负方向进行膨胀变形，而不能沿Z 轴的正方向膨胀变形，因此导致该位置应力较大，最大应力达到了575.38 MPa，是流固耦合下最大应力的2.4 倍。图7d 是螺杆转子在流热固耦合下的应力云图，其分布趋势与转子在热固耦合下的分布趋势相同，最大应力达到了559.95 MPa，相比热固耦合下的最大应力减少了2.7%。

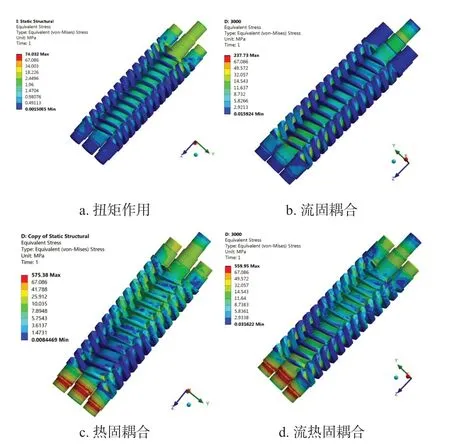
图7 螺杆转子的应力云图Fig.7 Stress cloud diagram of screw rotor

为了研究流热固耦合下三螺杆泵螺杆转子的应力变形规律，分析了5 种不同出口压力下转子变形和应力的变化规律，如图8 所示。由于两个从动螺杆转子的受力情况相同，因此仅对其中的一个从动螺杆进行受力分析，从图8a 中可以看出，从动转子的最大变形始终大于主动螺杆转子的最大变形，随着三螺杆泵出口压力的增大，主从动螺杆转子的最大变形也逐渐增大，可以发现两者之间的差值逐渐增大。从图8b 中可以看出，主动转子的最大应力始终大于从动转子的最大应力，且随着三螺杆泵出口压力的增大，主从动螺杆转子的最大应力也逐渐增大，主从动螺杆转子最大应力之间的差值也逐渐增大。

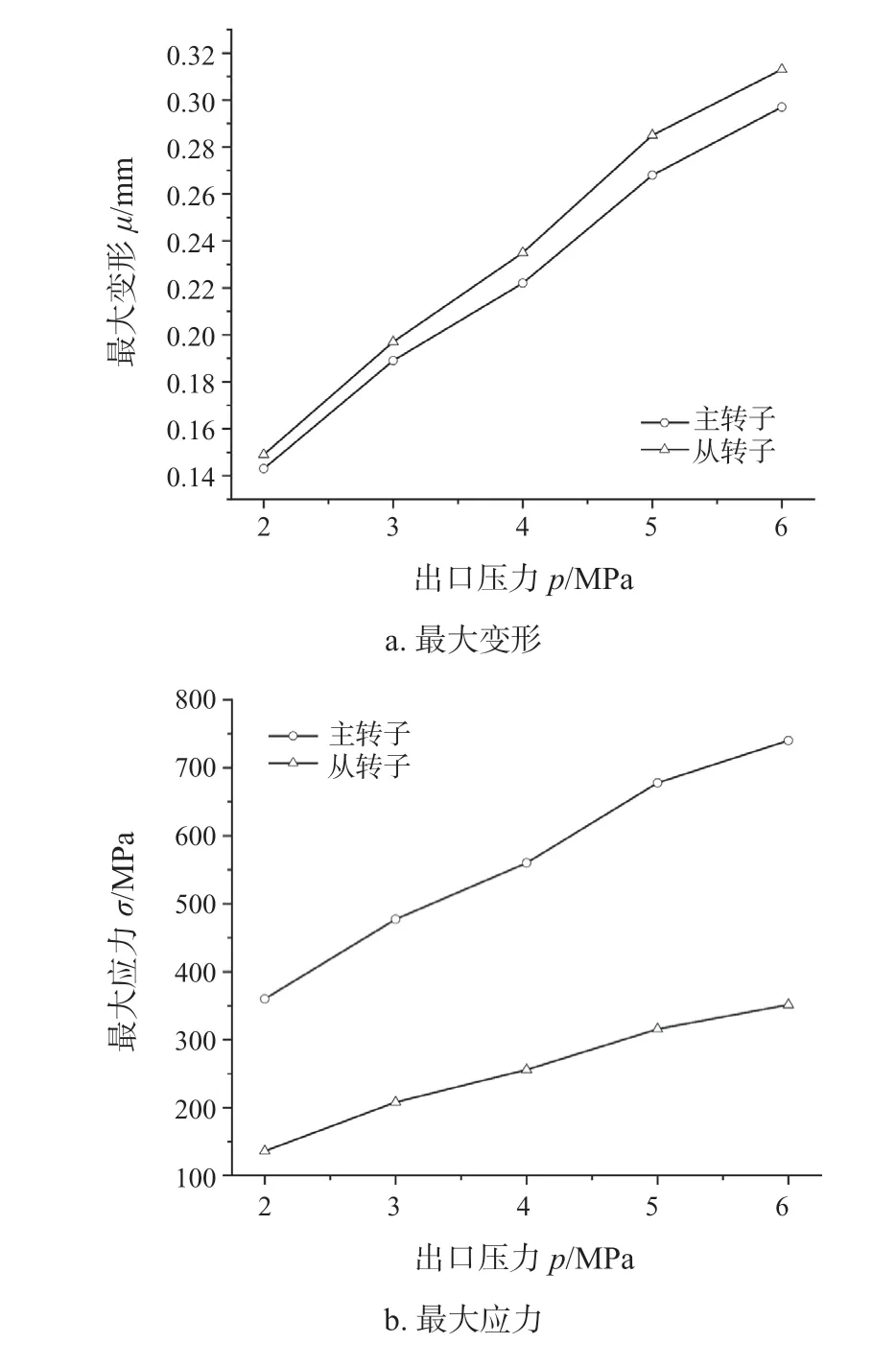
图8 不同出口压力下螺杆转子的应力变形规律Fig.8 The stress and deformation law of the screw rotor under different outlet pressures

图9 是三螺杆泵的主从动螺杆转子随转速的应力变形规律，从图9a 得到，主从动螺杆转子的最大变形随转速的增大都逐渐减小，从动螺杆转子的最大变形量始终大于主动螺杆转子的最大变形。从图9b得到，主动螺杆转子的最大应力始终大于从动转子的最大应力，随着转速的增大，主动螺杆转子的最大应力逐渐上升，但变化值较小，从动螺杆转子的最大应力随转速的增大逐渐减小。

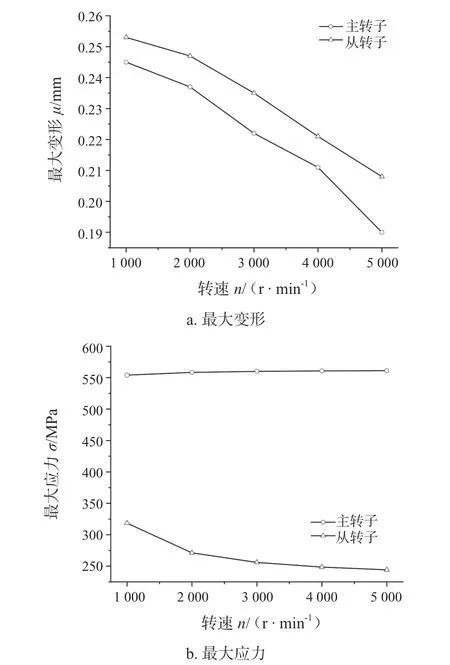
图9 不同转速下螺杆转子的应力变形规律Fig.9 The stress and deformation law of the screw rotor at different speeds

4.3 振动特性分析

为了研究螺杆泵中的压力载荷和温度载荷对转子振动的影响，对比了转子出口压力为4 MPa 下考虑和不考虑压力、温度载荷对转子振动的影响，如图10 所示。

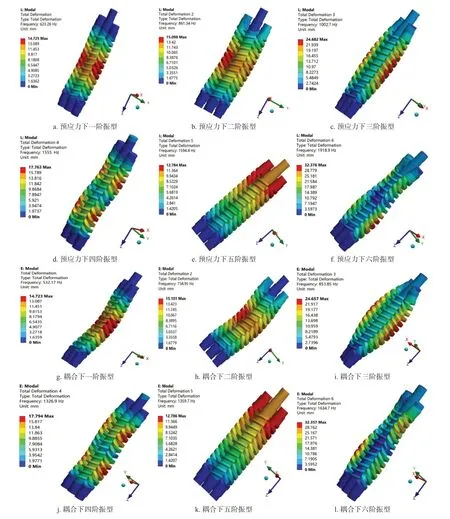
图10 不同耦合下转子模态振型Fig.10 Rotor modal vibration shapes under different couplings

从图中可以看出，主从动螺杆转子在预应力下的前六阶固有模态振型和耦合下的模态振型分布趋势基本相同，一阶模态主要是主从转子在垂直其轴线平面内发生弯曲变形，二阶模态振型主要是在其轴线所在平面发生弯曲变形，三阶模态主要是从动转子不同方向上发生弯曲变形，四阶模态主要是转子在同一方向发生的二次弯曲变形，五阶模态振型主要是转子发生扭转变形，六阶模态振型主要是从转子发生不同方向的二次弯曲变形。

通过表1 对比不同耦合方式下的模态频率，可以看出转子在流热固耦合下的前六阶模态频率均低于转子在预应力下的模态频率，说明螺杆泵产生的压力载荷和温度载荷对转子的振动频率有较大影响。当转速为3 000 r/min 时，通过下式计算，螺杆转子的激励频率为50 Hz，小于螺杆转子的一阶模态频率，因此不会发生共振。