新型小规模装备备件品种确定的犹豫模糊粗糙集决策方法
2022-06-08侯兴明陈小卫秦海峰张琳琳
杨 超,侯兴明,陈小卫,秦海峰,张琳琳
(1. 航天工程大学 航天指挥学院, 北京 101416; 2. 航天工程大学 航天保障系, 北京 101416;3. 陆军装甲兵学院士官学校 指挥管理系, 吉林 长春 130117)
确定备件品种是开展备件配置优化的基础,是明确备件需求的重要前提。备件品种的缺失会直接导致装备因备件短缺而停机,进而影响任务顺利实施;备件品种的冗余则会增加备件保障中人力、物力、财力的过量投入,导致保障效益低下。目前国内外对备件需求量和库存配置的研究较为丰富[1-4],而对备件品种确定方法的研究却很少。实际上,只有科学确定“备什么”,才能精准预测“备多少”,合理解决“备在哪”的问题。因此,开展备件品种确定方法的研究具有重要意义。
信息技术的快速发展、大量新型材料的广泛应用,使得新型装备技术复杂、高度集成、价值昂贵等特点尤为突出,加之新型装备往往呈分散型小规模部署、地域环境影响差异大等特点,使得装备故障数据缺乏、规律难以把握,从而给备件品种确定带来了较大的不确定性。传统的备件品种确定方法主要有逻辑决断法[5-6]、价值工程法[7-8]、可靠性分析法[9]、模糊综合评判法[10-12]和灰色系统理论分析法[13-14]等。但这些方法的决策信息输入值为单一确定值,新型小规模装备的上述特点,一方面使得在决策的过程中决策人员往往难以给出精确、全面的判断,决策信息的“模糊性”特点尤为突出;另一方面,决策成员专业知识、岗位经验及认识的不同,往往使得在决策过程中出现各有依据、各执己见的情况,难以达成一致意见,决策信息“犹豫性”特征非常明显。装备备件品种决策过程中决策信息这种典型的“犹豫性”和“模糊性”特点,使得难以将决策信息有效输入传统的方法当中,但忽略决策信息的任何特性,都很可能导致决策信息不完整,产生信息的遗漏,导致备件品种的缺失或冗余。现有的备件品种确定方法均未充分考虑新型小规模装备决策信息犹豫模糊性突出的典型特点[15-16],不能对其进行科学处理,有效辅助决策。
为解决上述问题,本文尝试将不确定性理论中处理不精确、不一致、不完备信息优势明显的犹豫模糊集理论和在知识划分与规则获取方面特点突出的粗糙集理论进行融合运用,构建新型小规模装备备件品种确定的犹豫模糊粗糙集模型,同时着眼最大适用性目标,给出备件品种确定规则的提取方法。
1 预备知识
1.1 犹豫模糊集
在多属性决策过程中,单个决策人员对属性进行评估时经常会对几个可能的取值犹豫不决,并且决策人员之间难以达成一致意见的情况十分普遍,这类决策信息被称为犹豫模糊信息。为了处理犹豫模糊信息,避免决策信息的丢失,得到合理的结果,Torra 和Narukawa提出了犹豫模糊集的概念,指出犹豫模糊集是模糊集的拓展形式,其每个元素是若干个可能值组成的集合[17-18]。徐泽水和Xia首次给出了犹豫模糊集的数学表达式[19-20]。
定义1设X为非空集合,则称
H={〈x,hA(x)〉|x∈X}
(1)
为犹豫模糊集,其中hA(x)是[0,1]上一些可能隶属值的集合,表示元素x对于集合A的隶属度的集合,h=hA(x)表示一个犹豫模糊元素。为方便,将X上所有犹豫模糊集构成的集合记为HF(X)。
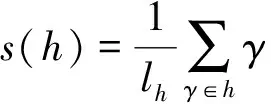
(2)
为h的偏差度,其中lh为h中元素的个数,γ为元素的值。对于两个犹豫模糊元素h1和h2,其比较和排序方法如下:
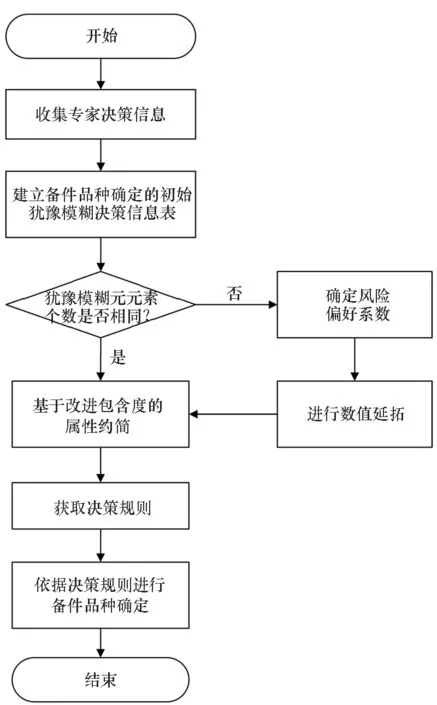
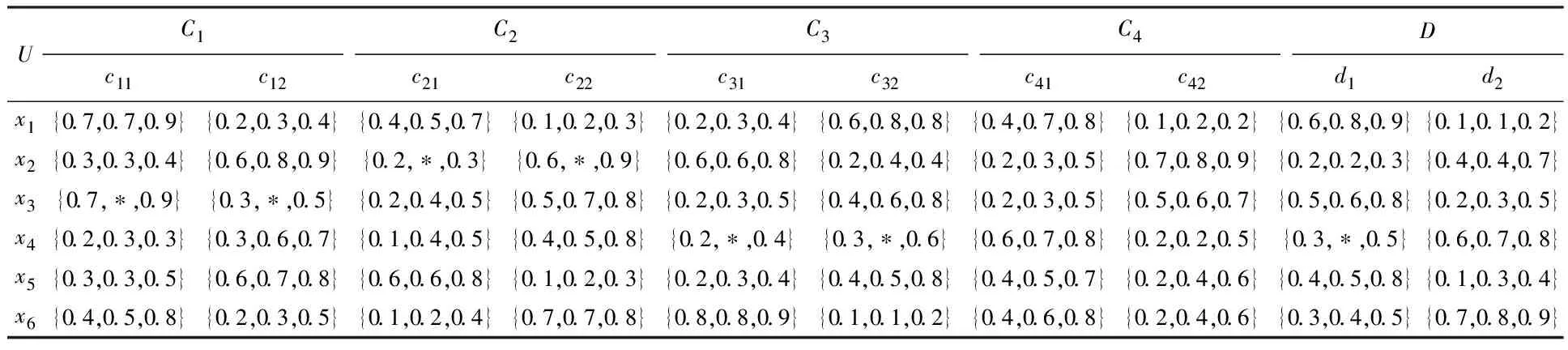
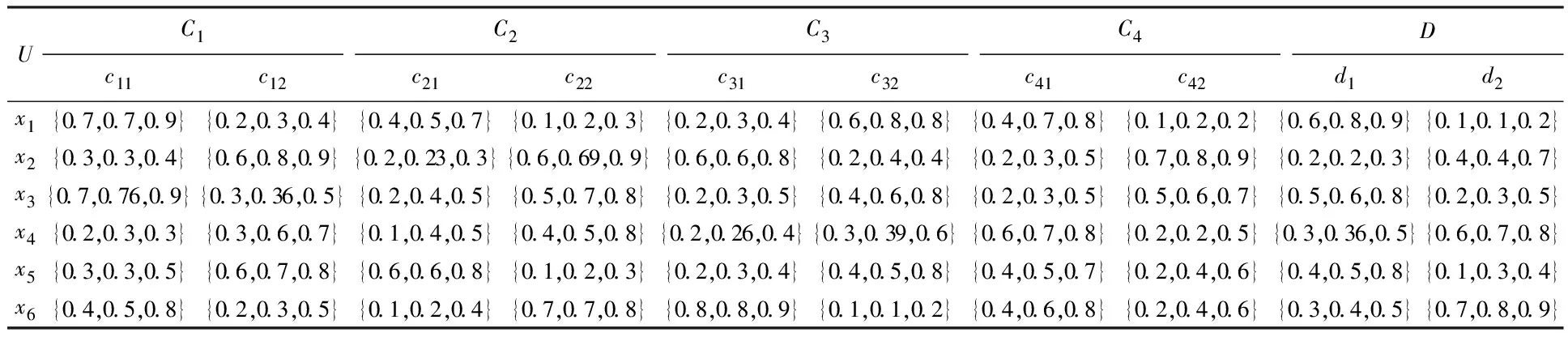
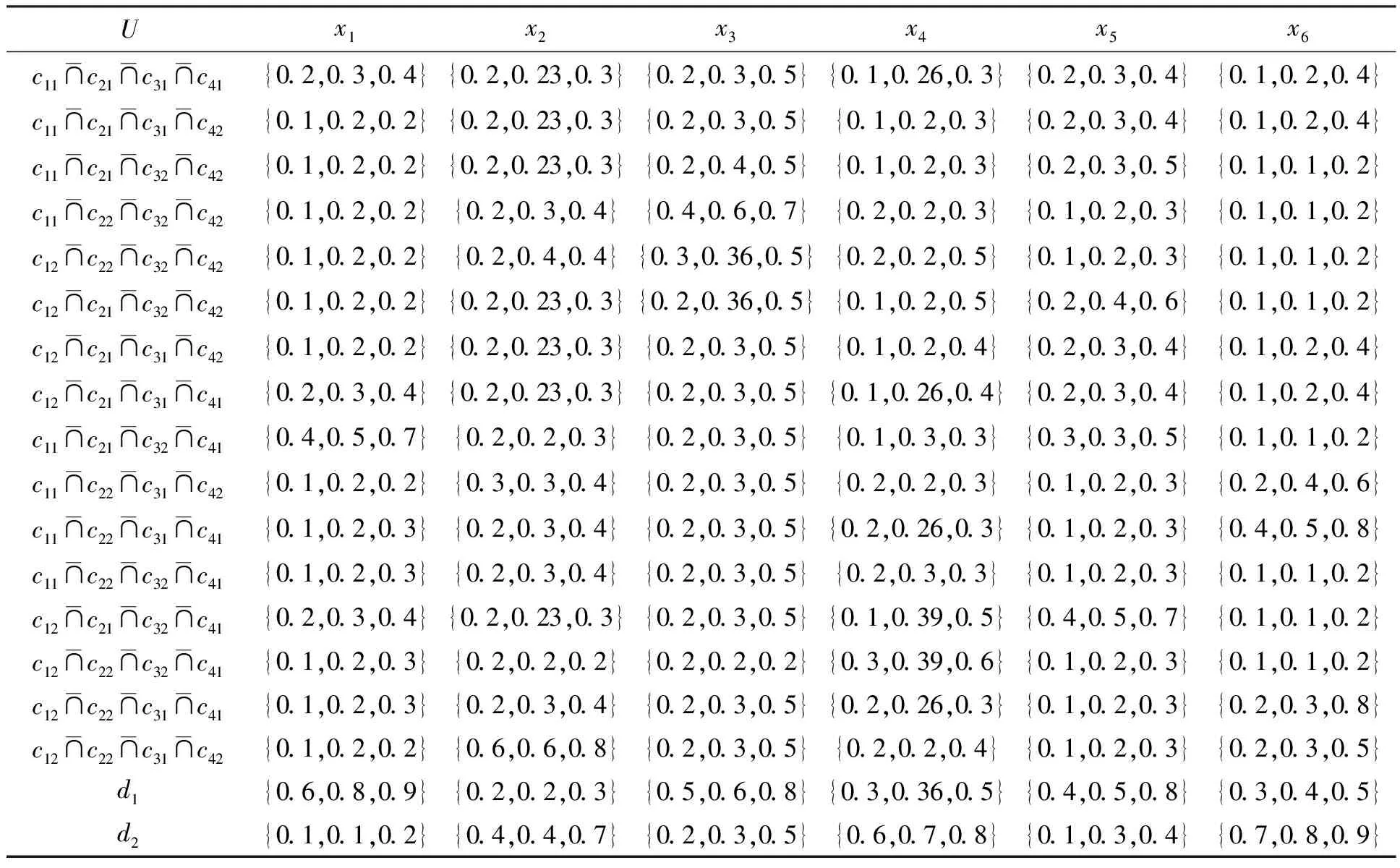
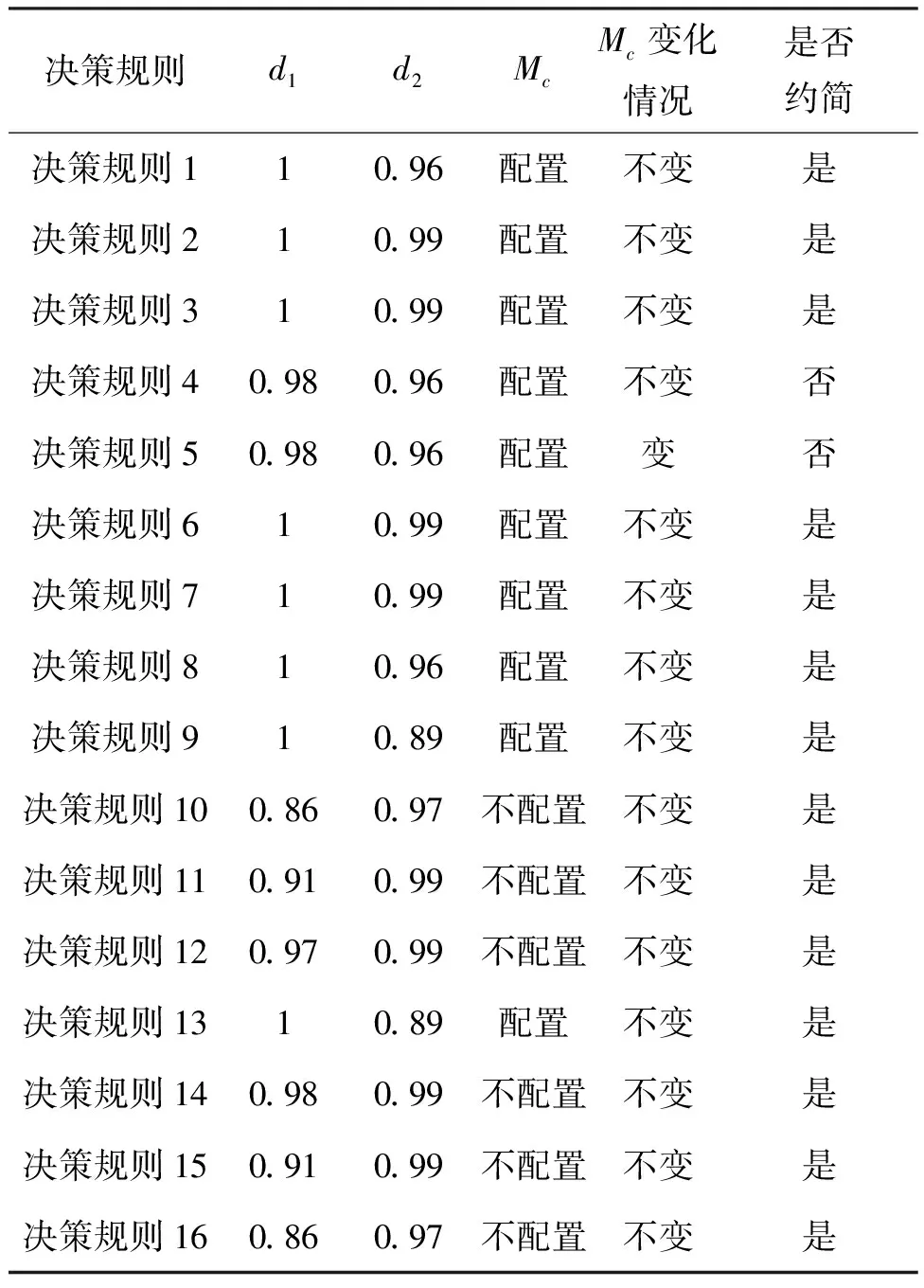
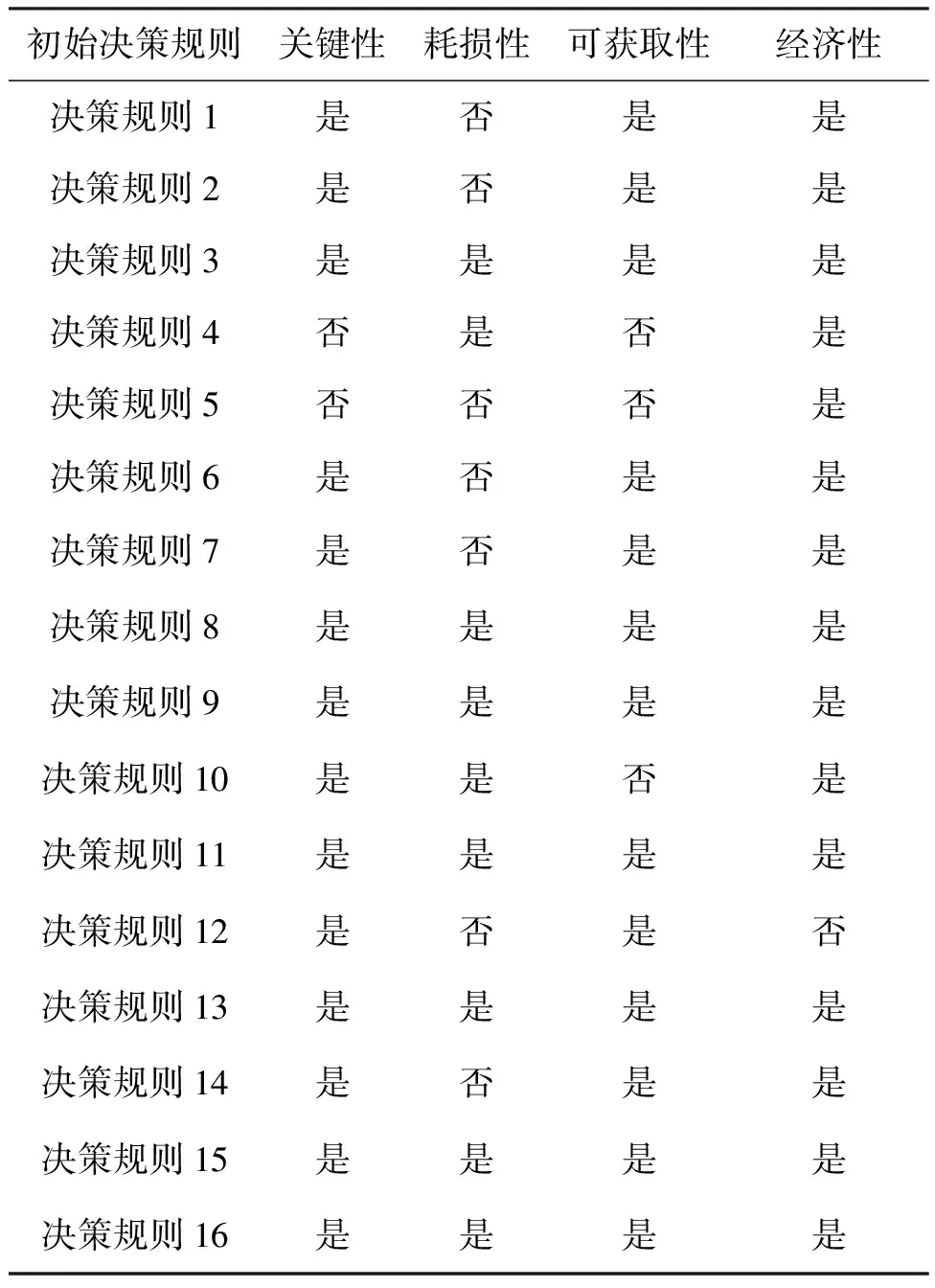
1)若s(h1) 2)若s(h1)=s(h2),则: 定义3设hA(x)和hB(x)为两个元素个数均为lh的犹豫模糊元,则二者的交、并关系运算[21]分别表示为: (3) (4) 由式(3)~(4)可知,两个犹豫模糊元相交后的元素为相交前各对应元素的较小值,两个犹豫模糊元相并后的元素为相并前各对应元素的较大值。 粗糙集理论由波兰数学家Pawlak教授提出,是一种处理含糊和不确定信息的新型数学工具。它以等价关系建立知识库,进而利用知识库中的上、下近似关系来描述“模糊”的概念,为知识获取和决策发现提供了新思路,其基本步骤是:建立决策信息表—利用等价关系求取上、下近似—属性约简—获取简化的决策规则。有关定义如下[22-23]。 当属性集A由条件属性集合C={c1,c2,…,c|C|}和决策属性集合D={d1,d2,…,d|D|}组成时,A=C∪D,V=VC∪VD,其中VC为条件属性值的集合,VD为决策属性值的集合,则称信息系统S为决策信息系统,也称决策信息表。 定义5设信息系统S=(U,A,V,f),B⊆A,则B在U上的等价关系RB为: RB={(x,y)∈U×U:f(x,a)=f(y,a),∀a∈B} (5) 若(x,y)∈RB,则称x和y关于B为等价关系,又称为不可区分关系。显然,这种等价关系满足自反性、对称性和传递性。等价关系RB将论域U划分为一些等价类,记为U/RB或U/B,包含元素x的等价类记为RB(x)或[x]RB。 当S为决策信息系统时,由条件属性集进行的划分称为条件类,由决策属性集进行的划分称为决策类。 R(X)={x∈U|[x]R⊆X} (6) (7) posR(X)=R(X) (8) (9) (10) 下近似是指由现有的知识判断必然属于X的对象组成的集合,也称为正域;上近似是指由现有知识判断可能属于X的对象组成的集合;负域是由现有知识判断肯定不属于X的对象组成的集合;边界域是上近似与下近似之差,即边界域是一个不可判定的区域。如果边界域为空集,则称X关于R是清晰的,反之则是粗糙的。 定义7设信息系统S=(U,A,V,f)中,a∈B⊆A,如果RB=RB-{a},则称属性a在B中是冗余的,否则称属性a在B中是必要的;如果B中的所有属性都是必要的,则称B是独立的;如果任意B′⊆B,都有RB=RB′,且B′是独立的,则称B′是B的一个约简,记为Red(B)=B′。 属性约简是指在不影响信息系统决策能力的前提下,通过消除冗余属性,提高信息系统潜在知识的清晰度,刻画条件属性和决策属性的内在联系,获得对决策更有效、使问题更简单的决策规则,从而依据获取的决策规则进行辅助决策。 很显然,约简集就是保持信息系统分类能力不变的最小属性子集,这些约简集的交集称为B的核心属性集,简称核或核属性,即: core(B)=∩Red(B) (11) 定义8设决策信息系统S=(U,C∪D,V,f),Xi和Yj分别代表U/C和U/D中的等价类,des(Xi)表示Xi对于各个条件属性值的取值,des(Yj)表示Yj对于决策属性值的取值,则决策规则定义为: rij:des(Xi)→des(Yj),Xi∩Yj≠∅ (12) 传统粗糙集决策方法仅适用于离散型确定值数据的决策信息,对犹豫模糊特征突出的新型小规模装备备件品种决策信息缺乏相应的处理能力。因此,本节将犹豫模糊集理论和粗糙集理论进行拓展融合,构建备件品种确定的犹豫模糊粗糙集决策模型。 参照粗糙集信息系统的基本形式,构造形如S=(U,A,V,f)的备件品种犹豫决策信息系统,其中U={x1,x2,…,x|U|}为某装备系统中所有待确定是否列入备件清单的备件品种;A=C∪D,C为备件品种确定的影响因素集,D为是否设置为备件的决策属性集,包括“设置”和“不设置”两个属性;f表示影响因素集与其属性值之间的映射关系,V表示决策人员对影响因素的评价值域,且值域为犹豫模糊集,则S为备件品种确定的犹豫模糊决策信息系统。 在决策过程中,往往会出现由于个别决策人员在某些方面知识经验的欠缺导致无法给出决策信息的情况,这样就会形成犹豫模糊元所包含的元素数量不一致的现象,进而影响决策计算和分析过程。为便于进行后续的计算和分析,需要采用一定的方法对元素较少的集合进行延拓。通常有两种方式[19]:一是用元素个数较少的犹豫模糊元中的最小值元素将犹豫模糊元补齐,称为悲观延拓法;二是用元素个数较少的犹豫模糊元中的最大值元素进行补齐,称为乐观延拓法。 在备件品种确定的决策过程中,往往需要根据备件保障的综合形势进行风险判断,而不能单纯地定位在悲观或乐观两个极端。为解决这一问题,本文提出一种基于风险偏好系数的数值延拓法。 设θ∈[0,1]为风险偏好系数,则犹豫模糊元h(x)中需延拓的元素hσ为: hσ=θh++(1-θ)h- (13) 式中,h+为h(x)中的最大值元素,h-为h(x)中的最小值元素。当θ=1时,hσ=h+,说明进行的是乐观评价,能够承担较大风险;当θ=0时,hσ=h-,说明进行的是悲观估计,不能够承担任务风险。因此,风险偏好系数θ越大,越能够承担风险,对决策结果的估计也就越乐观。延拓后的犹豫模糊元可记为: h(x)={hσ(1)(x),hσ(2)(x),…,hσ(n)(x)} (14) 其中,σ(1),σ(2),…,σ(n)为1,2,…,m的一个重新排列,一般按降序对hσ(i)(x)进行排列,hσ(i)(x)为h(x)中第i大的数值。 2.3.1 包含度的定义与计算 定义9[24]设任意集合A,B,C∈HF(X),若映射D:HF(X)×HF(X)→[0,1]满足下列条件,则称D为HF(X)上的包含度。 1)0≤D(B/A)≤1; 2)A⊆B⟹D(B/A)=1; 3)A⊆B⊆C⟹D(A/C)≤D(A/B),D(A/C)≤D(B/C)。 目前,只有极少量学者对犹豫模糊集的包含度计算进行了研究[21],经分析,现有的包含度计算有的基于得分函数,有的基于原始犹豫模糊元的交、并运算,但在实际运算中都存在一定的局限性。因此,根据包含度的公理化定义,本文首先基于风险偏好系数对犹豫模糊元的数值进行延拓,进而既考虑得分函数,又考虑数值延拓后的上下界元素的综合影响,给出犹豫模糊集包含度计算公式: (15) 证明: 1)显然,0≤D(B/A)≤1。 =1 =D(A/B) 同理,可证D(A/C)≤D(B/C)。 □ 2.3.2 属性约简条件与规则获取 (16) 称为决策条件选择在属性B上的投影。 设D(·/·)为犹豫模糊包含度,则对于B⊆A,记 (17) 定义11若对∀lj≤rj(j≤m),式MA(lj|aj∈A)=MB(lj|aj∈B)成立,则称B为犹豫模糊决策信息系统S的最大决策协调集。若B是S的最大决策协调集,且B的任何子集都不是S的最大决策协调集,则称B为S的最大决策约简集。 基于上述定义,给出犹豫模糊决策信息系统属性约简和决策规则的一般步骤: 输入:犹豫模糊决策信息表S=(U,A,V,f)。 输出:S的最大决策约简集和决策规则。 步骤1:计算所有决策条件选择,得到条件属性重新组合后的犹豫模糊决策信息表。 步骤2:计算组合后犹豫模糊决策信息表中条件属性在决策属性中的包含度。 步骤3:根据定义8,依据包含度获取决策规则。 步骤4:逐项删减条件属性,并计算新的决策规则,若规则不变,说明删减的条件属性冗余,则去掉并重复计算,以此类推;否则,说明条件属性为必要的,则保留,从而得到最大决策约简集。 2.3.3 模型计算流程 综上,可得基于犹豫模糊粗糙集的备件品种确定的基本流程如图1所示。 图1 基于犹豫模糊粗糙集的备件品种确定流程Fig.1 Process of determining the variety of spare parts based on hesitant fuzzy rough set 由于某新型小规模部署装备技术先进、构成复杂、数量较少且服役时间较短等特点突出,在确定其备件品种的决策过程中,决策人员难以给出准确的判断,且难以达成一致的意见,决策信息的犹豫模糊性十分明显。因此,本文采用基于犹豫模糊粗糙集的备件品种确定模型对其备件品种决策进行案例分析。 首先,建立决策专家组,明确备件品种确定的影响因素及属性表示。选取装备维修保障机关主管人员1人、装备维修保障一线技术人员1人、装备研制单位技术人员1人,共计3人组成决策专家组,以文献[15-16]的备件品种确定影响因素为初始参考,结合装备特点及备件决策实际,采用德尔菲法明确该装备备件品种确定过程中必须考虑的影响因素。经过多轮意见征询,整合得该装备信号处理分系统备件品种确定有零部件的关键性、耗损性、可获取性和经济性4个影响因素。 设论域U={x1,x2,x3,x4,x5,x6}为该装备信号处理分系统6种待确定是否列为备件的零部件;条件属性C={C1,C2,C3,C4}为备件品种确定的4个影响因素,各影响因素及其属性值符号如表1所示;决策属性D={d1,d2}={配置,不配置}。 表1 备件品种确定影响因素及属性表示 其次,收集专家决策信息,建立备件品种确定的犹豫模糊决策信息系统。其中,专家对每个属性的评价可以相同,对无法进行判断的属性可以不作出评价,具体决策情况如表2所示。由表中数据可知,由于该装备属于新型装备,加之个别专家知识、经验的欠缺,在决策过程中无法对某些属性作出判断,故以“*”表示其空值的属性。 为了便于计算和分析,需要对以“*”构成的犹豫模糊信息进行数值延拓。考虑该装备任务实际和单台独套的特点,不宜承担较高备件品种短缺的风险,结合经济性要求,将风险偏好系数θ定为0.3,按照本文基于风险偏好系数的数值延拓方法,对表2中的空值进行数值延拓,具体如表3所示。 表2 备件品种确定的犹豫模糊决策信息表 表3 数值延拓后的犹豫模糊决策信息表(θ=0.3) 表4 条件属性重组后的犹豫模糊决策信息表 =(0.6+0.9)+(0.2+0.3)+(0.5+0.8)+ (0.3+0.5)+(0.4+0.8)+(0.3+0.5) =(0.6+0.9)+(0.6+0.8)+(0.5+0.8)+ (0.3+0.5)+(0.4+0.8)+(0.3+0.5) =7 根据包含度计算结果获取决策规则,如表5所示。 由表5可逐条得出如下备件品种确定的初始决策规则。 规则1:若零部件为关重、易耗损、易购且贵重件,则需配置备件。 规则2:若零部件为关重、易耗损、易购且价格一般件,则需配置备件。 规则3:若零部件为关重、易耗损、难购且价格一般件,则需配置备件。 规则4:若零部件为关重、不易耗损、难购且价格一般件,则需配置备件。 规则5:若零部件为关键性一般、不易耗损、难购且价格一般件,则不需配置备件。 规则6:若零部件为关键性一般、易耗损、难购且价格一般件,则需配置备件。 规则7:若零部件为关键性一般、易耗损、易购且价格一般件,则需配置备件。 表5 组合条件属性在配置决策中的包含度与决策规则 规则8:若零部件为关键性一般、易耗损、易购且价格贵重件,则需配置备件。 规则9:若零部件为关重、易耗损、难购且贵重件,则需配置备件。 规则10:若零部件为关重、不易耗损、易购且价格一般件,则不需配置备件。 规则11:若零部件为关重、不易耗损、易购且贵重件,则不需配置备件。 规则12:若零部件为关重、不易耗损、难购且贵重件,则不需配置备件。 规则13:若零部件为关键性一般、易耗损、难购且贵重件,则需配置备件。 规则14:若零部件为关键性一般、不易耗损、难购且贵重件,则不需配置备件。 规则15:若零部件为关键性一般、不易耗损、易购且贵重件,则不需配置备件。 规则16:若零部件为关键性一般、不易耗损、易购且一般件,则不需配置备件。 显然,上述决策规则过于冗余,不便于实际操作,需要对其进行属性约简,获取更加简洁、便于操作的决策规则。因此,根据定义11和属性约简步骤,逐项删减条件属性,并计算剩余组合条件属性在决策中的包含度和决策规则,通过决策规则的变化情况判定是否为可约简属性,从而得到最佳约简集和最简决策规则。 以去除“关键性”属性为例,计算剩余组合条件属性在决策中的包含度和决策规则,结果如表6所示。通过逐条比较决策规则的变化情况来判定该属性在该决策规则中是否可以约简,判定原则为:若决策规则较去除属性前发生变化,则不可约简;若不发生变化,则可约简;若存在二义性,同样判定为不可约简,如表6中的决策规则4和决策规则5,去除“关键性”属性后两者的组合条件属性相同,单纯看决策规则4去除“关键性”属性后决策规则变化情况,关键性属性可约简,而单纯看决策规则5则为不可约简,出现了组合条件属性相同下的判定二义性,为确保决策结果的正确性,此种情况下均判定为不可约简。 表6 去除“关键性”属性后组合条件属性在决策中的包含度及决策规则变化情况Tab.6 Change of inclusion degree and decision rules of combine conditional attributes in configuration decisions except "key"attribute 按照同样的方法,分别去除“耗损性”“可获取性”和“经济性”属性指标,根据判定规则逐条比较决策规则的变化情况,便可得到各属性在决策规则中的可约简情况,如表7所示。 表7 条件属性是否可约简情况一览表 由表7可知,决策规则3、8、9、11、13、15、16的所有条件属性均可约简,说明上述决策规则为冗余规则,可去除;决策规则1、2、6、7、14可约简的条件属性相同,说明可整合;决策规则4、5、10、12都具有唯一性,均需保留。根据可约简情况对16条决策规则进行去除和约简后,便得到最大决策约简集和决策规则,具体如下: 决策规则1、2、6、7、14整合约简后的最大决策约简集为c21,约简后的决策规则为:若零部件为易损耗件,则进行配置。 决策规则10经约简后的最大决策约简集为c31,相应的决策规则为:若零部件为易购件,则不需配置备件。 针对新型小规模装备备件品种确定过程中决策信息“犹豫性”和“模糊性”特点突出、难以作为传统备件决策方法有效输入的情况,提出运用犹豫模糊集和粗糙集理论相结合的方法进行备件品种确定。考虑备件品种确定中风险的承受能力,故引入风险偏好系数对不完备的犹豫模糊决策信息进行数值延拓。综合犹豫模糊决策信息的得分函数和数值延拓后数值变化的影响,给出了改进的包含度计算公式并进行了证明。基于包含度,给出了备件品种确定属性约简条件和决策规则获取步骤。以某型小规模装备备件品种确定任务为例进行了方法验证,形成了备件品种确定的决策规则集,为充分利用备件品种确定中的犹豫模糊决策信息提供了一定的理论支撑和方法参考。为进一步提高方法的精确性,后续应对以下问题开展深入研究:一是科学确定风险偏好系数的最佳取值方法,增强风险控制的精准性;二是研究开发配套计算程序,提高备件品种确定的高效性。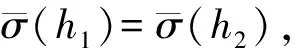

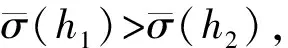
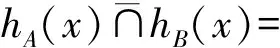
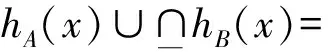
1.2 粗糙集

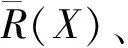
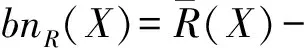
2 基于犹豫模糊粗糙集决策的备件品种确定模型
2.1 构建备件品种确定的犹豫模糊决策信息系统
2.2 基于风险偏好系数的数值延拓
2.3 基于改进包含度计算的属性约简和规则获取
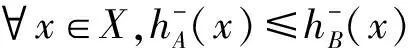
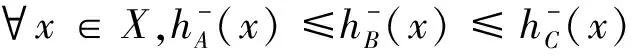
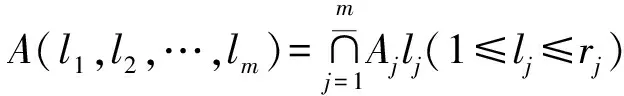
3 案例分析

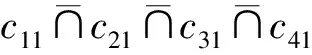
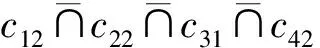

4 结论
