面向时空交通栅格流量预测的3D通道注意力网络
2022-06-08童凯南林友芳郭晟楠万怀宇
童凯南,林友芳,刘 军,郭晟楠,万怀宇
(1. 北京交通大学 计算机与信息技术学院, 北京 100044; 2. 中国民航信息网络股份有限公司, 北京 101318)
在现代智能交通系统[1](intelligent transportation systems, ITS)和高级旅行者信息系统(advanced traveler information systems, ATIS)中,交通流量预测任务能够为政府、出租车公司和游客提供准确可靠的信息,起到至关重要的作用[2-3]。例如,政府的交通管理部门可以通过预测交通流量高峰出现的时间和地点来提前采取相应的交通管理措施[4]。出租车公司可以通过预测未来的交通流量来优化车辆调度任务。此外,游客也可以根据预测的交通状况制订合理的出行计划[5]。因此,准确预测交通流量对保障社会安全,促进经济发展和提升游客出行体验有重大意义。
现有交通数据预测模型大致可以分为两类:传统方法和深度学习方法。传统的统计或机器学习方法如XGBoost[6]等缺乏处理高维的空间数据能力,无法学习交通数据中复杂的非线性信息。不过随着深度学习的发展,使得这些问题可以逐渐被解决[7]。
递归神经网络[8](recurrent neural network, RNN)能够建模数据中的时间信息。其变体长短期记忆神经网络[9](long short-term memory, LSTM)和门控循环单元[10](gated recurrent unit, GRU)进一步增强了这种能力。最近,文献[2,11]使用基于LSTM的网络来预测短期交通速度和交通流量,基于长短期记忆网络的关联时间序列预测[12](correlated time series oriented neural network based on LSTM, CTS-LSTM )模型考虑了多个序列之间的相关性。此外,空间相关性对交通数据预测至关重要,却很少有基于LSTM的方法能对其进行建模。
幸运的是,研究人员找到了使用卷积神经网络(convolutional neural networks, CNN)来捕获空间信息的解决方案,例如卷积长短期记忆网络[13](convolutional LSTM, ConvLSTM)模型和深度时空残差网络[14](spatio-temporal residual networks, ST-ResNet)模型。它们不仅能捕获空间相关性,还能捕获时间相关性。此外,基于注意力机制的时空图卷积[15](attention based spatial-temporal graph convolutional networks, ASTGCN )模型和时空同步图卷积[16](spatial-temporal synchronous graph convolutional networks, STSGCN )模型等基于图卷积(graph convolutional networks, GCN )的模型性能也很强大,不过并不适用于本研究聚焦的栅格数据预测问题。

图1 CNN在城市交通流量预测分析中的应用Fig.1 Applications of CNNs for citywide traffic flow analytics
近年来,ST-3DNet[17]和DeepSTNPlus[18]模型都在交通栅格流量预测问题上取得了进展。然而,与其他基于CNN的模型一样受到卷积核大小的限制,它们都无法有效地捕获远程空间相关性。如图1所示,在办公区上班的人们可能住在远近不同的住宅区A和B,这些区域之间就会因为通勤而存在很强的相关性,这就需要模型能够捕获大范围甚至全局的时空联系。一些研究试图通过堆叠多层CNN来解决此问题,但这样会使得模型训练变得非常困难。在文献[19-23]中,自注意力机制可以用来捕获全局范围的空间相关性,但并不能对不同通道捕获不同的相关性,于是本文提出3D通道内注意力单元(three-dimensional inner channel attention, 3D-InnerCA)来学习每个通道内的全局时空相关性。
此外,受SENet[24]计算CNN特征通道之间相互关系的启发,ST-3DNet设计了一个重新校准模块,以探索每个区域上各个通道的贡献,不过这些贡献是静态学习得到的,并不能很好地适应数据的动态性。假设有一个特征通道关注的是某些复杂的交通情景,比如立交桥。那么在有立交桥的区域,这个特征就比其他特征有更大贡献。相应的,这个特征在有立交桥的区域也比在其他区域更具重要性。需要强调的是,上述关系也是动态变化的。例如,人们可能在周末外出郊游,那么某些关注通勤状况的特征在周末就会变得不那么重要。而现有交通栅格流量预测模型无法应对上述情况。因此本文在此基础上设计InterCA,从而动态计算各个特征通道在每个区域上的贡献。
1 问题定义
在本节中给出本文中使用的一些定义。
定义1交通栅格流量。通过将城市划分为I×J的栅格图,每个栅格就代表城市的一个区域,Cin个通道代表Cin种类型的交通数据,例如流入流量、流出流量。此时的交通栅格流量的形式就像一张图片,可以得到第t时间段内的数据Xt∈RCin×I×J。
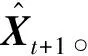
2 模型结构
2.1 总体架构
为更有效地捕获时空相关性,提出一种基于深度学习的端到端模型3D-CANet。模型总体架构如图2所示。首先使用一层卷积核大小为1×3×3的3D卷积来捕获数据的局部特征。之后堆叠3个3D-InnerCA单元以捕获全局时空动态相关性。接下来,使用一层有C个大小为3×3×3卷积核的3D卷积层,用于聚合时间维度上的信息。此时,时间信息已被充分捕获,为进一步探索全局空间动态相关性[17],堆叠2个2D空间通道内注意力单元(2D spatial inner channel attention,2D-s-InnerCA)。最后,使用InterCA单元来动态地计算每个区域上各特征通道的贡献。
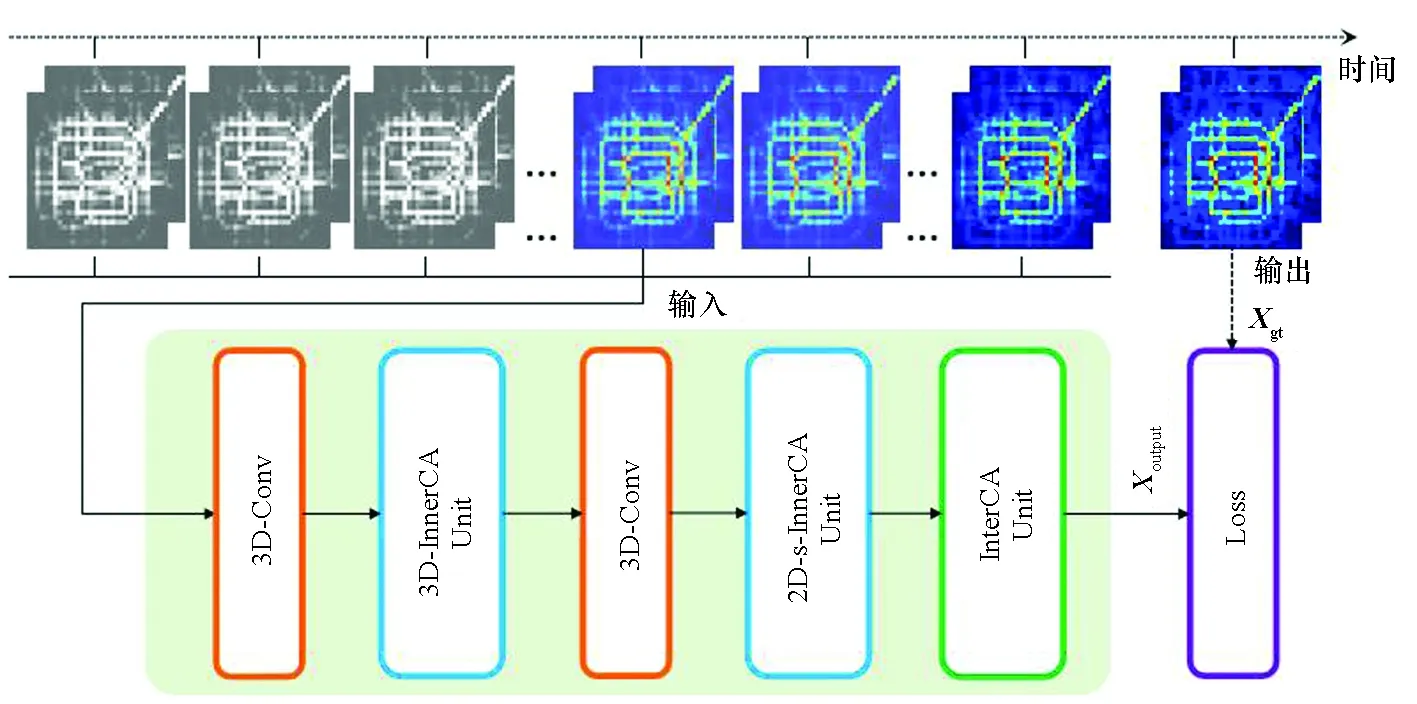
注:3D-Conv为3D卷积;3D-InnerCA Unit为3D通道内注意力单元;2D-s-InnerCA Unit为2D空间通道内注意力单元;InterCA Unit为通道间注意力单元。图2 3D-CANet模型的整体架构Fig.2 Overall architecture of 3D-CANet
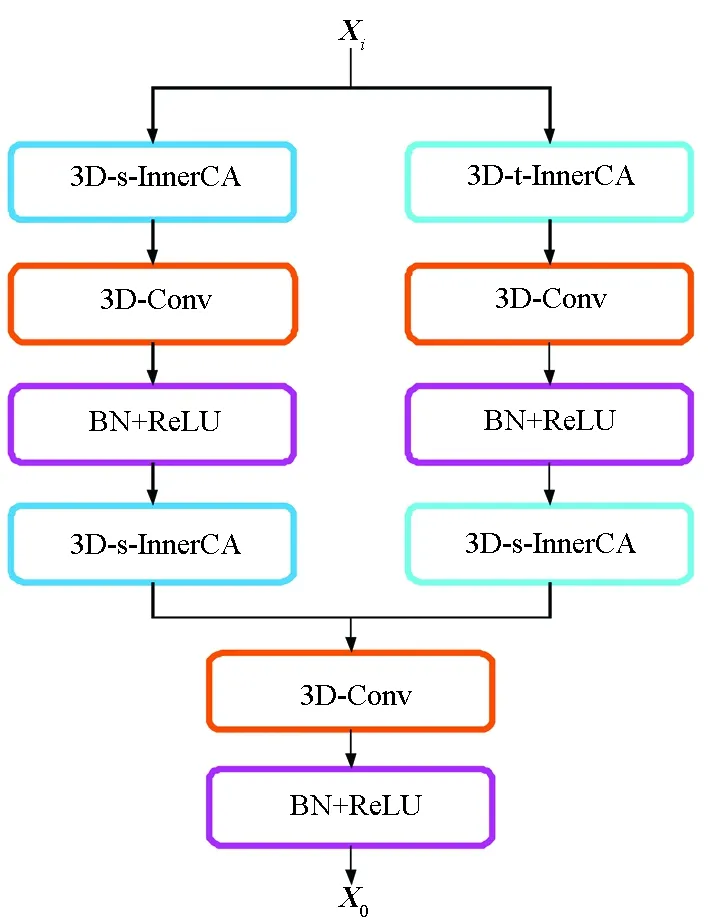
图3 3D通道内注意力单元Fig.3 3D-InnerCA unit
2.2 3D-InnerCA
由于交通栅格流量具有动态的全局时空相关性,基于CNN的模型受卷积核大小的限制,并不能捕获大范围的信息。并且由于参数固定,模型不具有自适应输入数据的动态能力,因此它们不能充分学到数据中蕴含的信息。如图3所示,提出一个能动态探索各个特征通道内的全局时空相关性的模块,称为3D-InnerCA,其中BN+ReLU表示批归一化和激活函数ReLU。文献[19-23]提出的模型大多使用自注意力机制来捕获栅格流量中的空间信息,可以动态计算每个区域和其他所有区域之间的相关性,但这种相关性对于所有通道是共享的。考虑到不同的特征通道中时空相关性可能有所区别,因此在3D-InnerCA单元中对通道进行分组,以学习分组后各个通道内的动态全局相关性。具体来说,3D-InnerCA单元由3D-s-InnerCA和3D时间通道内注意力单元(3D temporal inner channel attention,3D-t-InnerCA)组成,分别用来动态捕获全局空间相关性和时间相关性。将两个部分的结果拼接成2C个通道,并使用大小为3×3×3的C个卷积核进行3D卷积,从而把2C个通道聚合为C个通道。为保证训练效率,结构中使用残差学习[25]。
2.2.1 3D-s-InnerCA
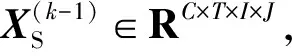
(1)
(2)
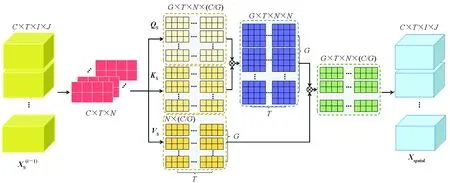
图4 3D空间通道内注意力Fig.4 3D-s-InnerCA
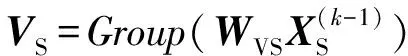
(3)
(4)
其中,WQS、WKS和WVS是全连接层的参数。这里不像传统的注意力那样使用激活函数Softmax,因为它会限制模型的表达能力并增加训练成本[26]。需要注意的是,2D-s-InnerCA的结构与3D-s-InnerCA类似,只是没有时间维度上的操作。
2.2.2 3D-t-InnerCA
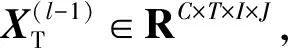
(5)
(6)
(7)
(8)
其中,WQT、WKT和WVT是全连接层的参数。
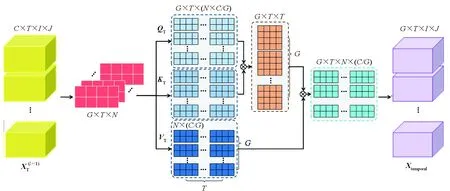
图5 3D时间通道内注意力Fig.5 3D-t-InnerCA
2.3 InterCA
由于交通流量中复杂的相关性,不同特征通道对同一个区域的贡献不同,而同一个特征对不同区域的重要性也不同。不仅如此,特征通道的贡献还会随着时间而动态变化。因此,提出通道间注意力单元,并使用2D卷积神经网络来动态学习每个区域上特征通道之间的关系。
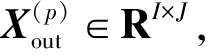
(9)
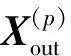
(10)
其中,“∘”是逐元素乘法。将全部Cout个通道拼在一起,则3D-CANet最终输出预测结果Xout∈RCout×I×J。
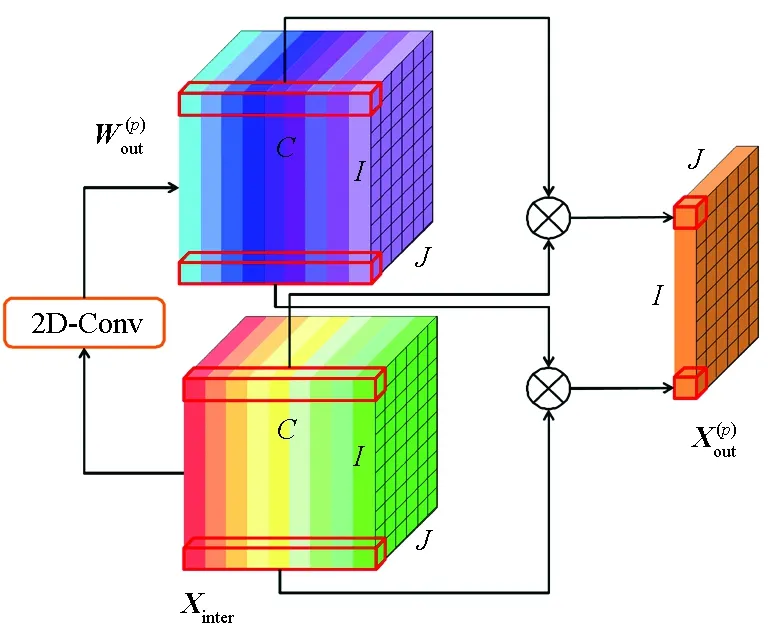
图6 通道间注意力单元Fig.6 Inter-channel attention unit
2.4 损失函数
模型通过最小化损失函数来进行训练,损失函数为预测值与真实值之间的均方误差,即
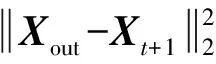
(11)
3 实验
在3个不同的交通流量数据集上进行实验,与基准模型相比,实验结果证明了3D-CANet模型的有效性。
3.1 数据集
本研究使用TaxiBJ、BikeNYC和TaxiNYC 3个交通流量数据集,它们的统计信息如表1所示。
1)TaxiBJ:TaxiBJ数据集由轨迹数据和外部因素数据组成。其中轨迹数据是在四段时间内的北京出租车GPS数据,包括:2013年7月1日—2013年10月30日,2014年3月1日—2014年6月30日,2015年3月1日—2015年6月30日和2015年11月1日—2016年4月10日。每个时间段的长度设定为30 min。将轨迹数据转化为栅格数据,并选取后4周数据为测试集,其余数据为训练集。
2)BikeNYC:像TaxiBJ一样,BikeNYC数据集由轨迹数据和外部因素数据组成。其轨迹数据来源于纽约自行车系统,时间跨度为2014年4月1日—2014年9月30日。每个时间段的长度设定为1 h。将轨迹数据转化为栅格数据,并选取最后10 d的数据为测试集,其余数据为训练集。
3)TaxiNYC:TaxiNYC数据集由22 349 490条纽约出租车行驶数据组成,时间跨度为2015年1月1日—2015年3月1日。每个时间段的长度设定为30 min。将轨迹数据转化为栅格数据,并选取最后20 d为测试集,其余数据为训练集。
3.2 基准模型
将3D-CANet与以下8个基准模型进行比较:
1) HA:如同文献[14,17,27]的做法,将每个区域历史数据中对应时间段的均值作为该区域流入和流出流量的预测值。
2) XGBoost[6]:一种提升树的可扩展机器学习系统,属于机器学习方法,能够根据各个区域的历史数据进行预测。
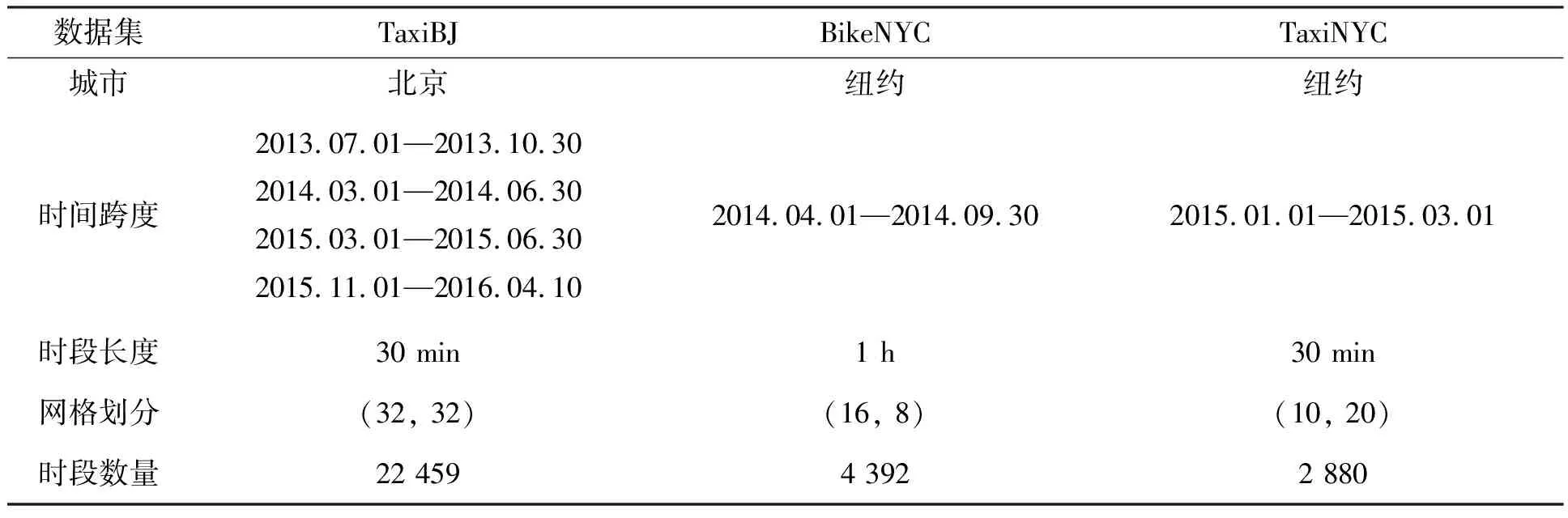
表1 交通流量数据集的统计信息
3) LSTM[9]:长期短期记忆网络是一种RNN网络,用于时间序列预测,能够根据各个区域的历史数据进行预测。
4) GRU[10]:门控循环网络也是一种RNN网络,用于时间序列预测,能够根据各个区域的历史数据进行预测。
5) ConvLSTM[13]:ConvLSTM结合CNN和LSTM,可以像CNN一样捕获空间信息,也能像LSTM一样挖掘时间信息,且能同时对全部区域的历史数据进行时空信息提取并预测。
6) ST-ResNet[14]:它是一种基于深度神经网络的时空数据预测模型。使用3个残差网络分别建模近邻性、周期性和趋势性的空间相关性,然后融合3个部分的结果最终输出。
7) ST-3DNet[17]:基于深度神经网络的时空数据预测模型。它首先利用3D卷积在时间和空间维度上捕获信息。与ST-ResNet不同,它仅考虑近邻性和趋势性,然后进行融合输出。
8)DeepSTNPlus[18]:基于深度神经网络的时空数据预测模型。它在整个模型最开始就进行近邻性、周期性和趋势性的融合,然后在模型末尾使用多尺度融合网络来融合多级别特征,展现出城市流量预测任务的最佳性能。
3.3 参数设置
本文基于PyTorch[27]实现3D-CANet模型。在本研究中,预测两种交通数据:流入和流出流量。因此,Cin设定为2。设置输入数据的长度为6,也就是模型根据最近6个时间段内的数据以进行预测。使用最大值最小值归一化方法将输入数据缩放到[-1,1]范围内。在TaxiBJ、BikeNYC和TaxiNYC上,分别选择最近4周、10 d和20 d的数据作为测试集,其他数据作为训练集。在3个数据集上训练的批大小分别为4、8、4,学习率为0.01。计算预测值和真实值的均方根误差(root mean square error, RMSE)和绝对平均误差(mean absolute error, MAE)作为评价指标:
(12)
(13)
其中,N为所有预测值的数量。
在TaxiBJ、BikeNYC和TaxiNYC上,3D-CANet的第一层3D卷积分别使用16、64和64个卷积核。在探索不同数量并考虑训练开销的情况下,设定在模型中堆叠3个3D-InnerCA单元和2个2D-s-InnerCA单元,每个单元分别有2层注意力。其他的3D卷积都应用C=64个大小为3×3×3的卷积核,2D卷积都使用C=64个大小为3×3的卷积核。
3.4 实验结果比较分析
首先给出3D-CANet在3个数据集上与其他8个基准模型的比较,结果如表2所示。模型根据最近6个时间段来预测下一个时间段的数据,其中ST-ResNet和DeepSTNPlus分别另有3个周期性和趋势性数据,ST-3DNet有3个趋势性数据。运行每个模型5次,并计算出评价指标的平均值和标准差。结果表明,本文提出的模型性能比其他基准模型更优。对于ST-ResNet、ST-3DNet和DeepSTNPlus模型,它们除了要有近邻性数据还需要获取周期性和趋势性信息;而3D-CANet模型仅需要近邻性数据就能获得更好的性能。这表明3D-CANet模型比基准模型能更有效地捕获时空特征。实际上每个基准模型都有自身的特点。HA、XGBoost、LSTM和GRU只能预测单个区域的序列数据,并且都不能建模空间相关性。ConvLSTM、ST-ResNet、ST-3DNet和DeepSTNPlus等模型确实可以捕获空间和时间信息。然而受卷积核大小的限制,它们并不能很好地捕获全局信息。因此在城市范围更大、栅格数量更多的TaxiBJ数据集上,它们的性能与3D-CANet差距更大。相对的,3D-CANet使用3D-InnerCA单元,能够利用注意力机制动态捕获各个特征通道内的全局时空信息。此外,模型的Inter-CA可以动态学习每个区域上各特征通道的贡献,更增强了其表征能力。
3.5 模型分析
3.5.1 多步预测比较
图7显示了3D-CANet模型与基准模型在三个数据集上的多步预测结果。模型要预测未来1至6个时间段的数据,每个时间段为1 h。可以看出,预测时间越长,两种评价指标就越大。结果表明,本文提出的模型在所有模型中表现最好,这证明了3D-InnerCA单元捕获全局信息的能力。此外,InterCA可以动态计算每个区域上不同特征通道的贡献,这使得本文提出的3D-CANet模型更加强大。
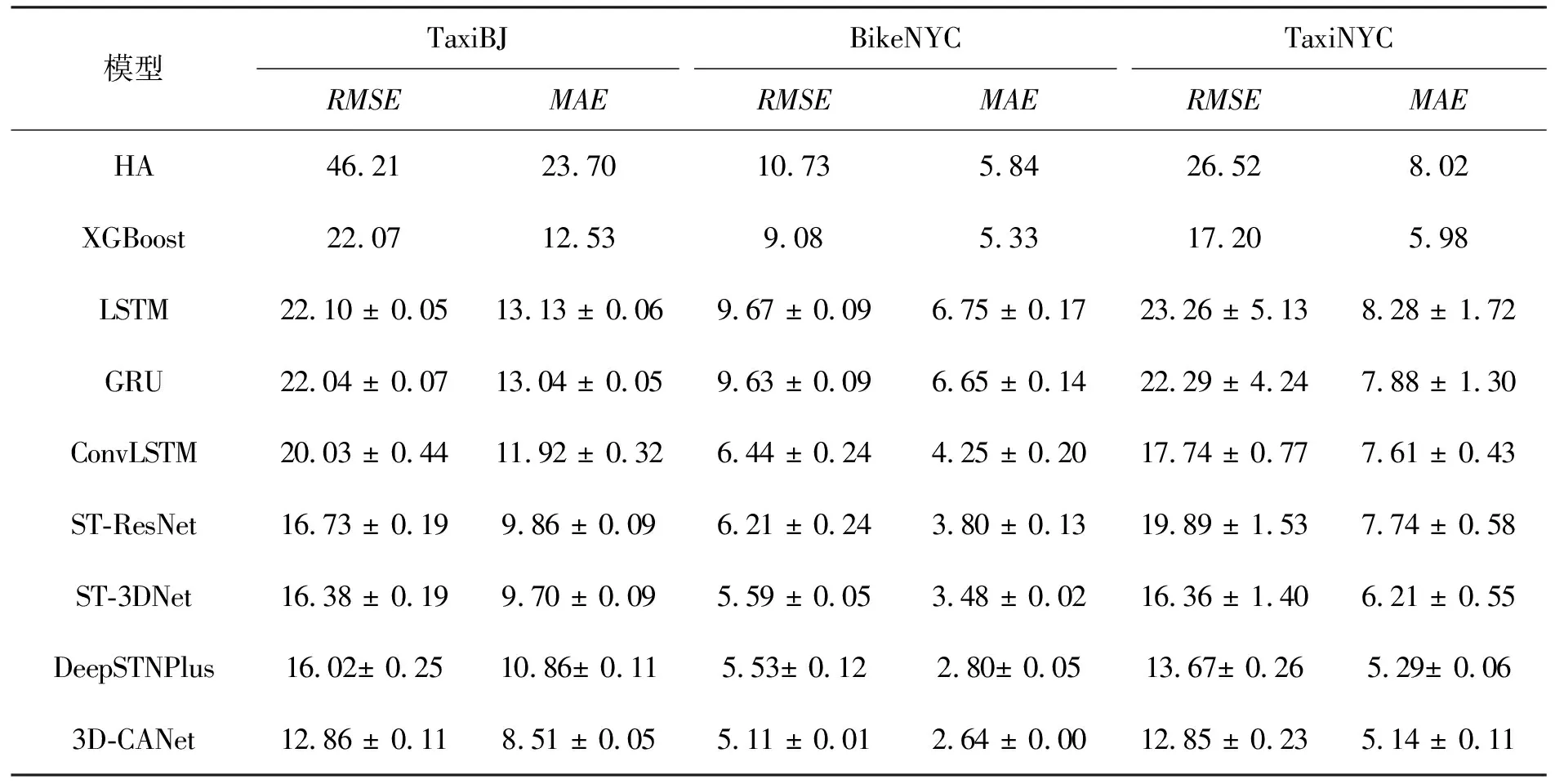
表2 三个数据集上的预测结果
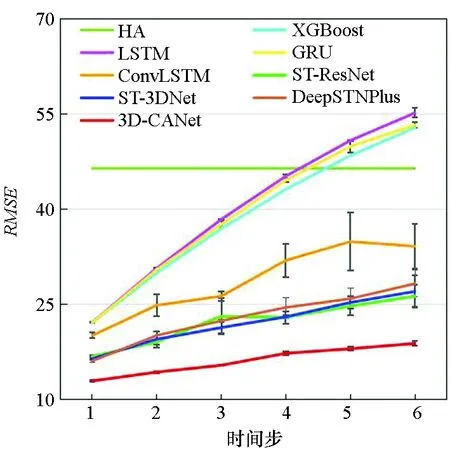
(a) TaxiBJ的RMSE(a) RMSE on TaxiBJ
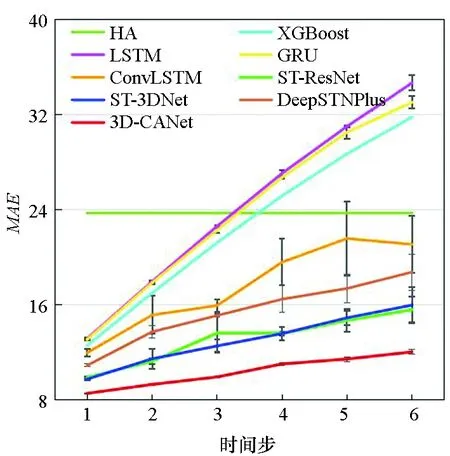
(b) TaxiBJ的MAE(b) MAE on TaxiBJ
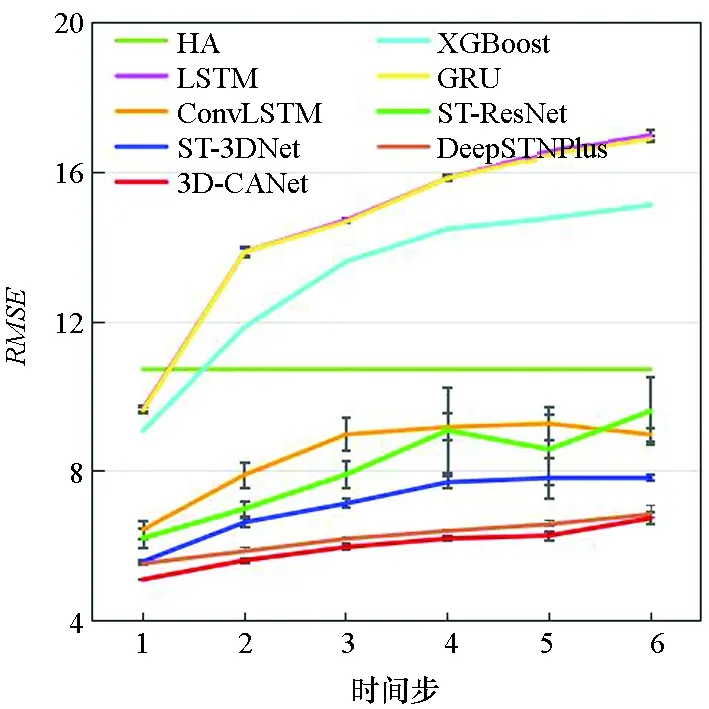
(c) BikeNYC的RMSE(c) RMSE on BikeNYC
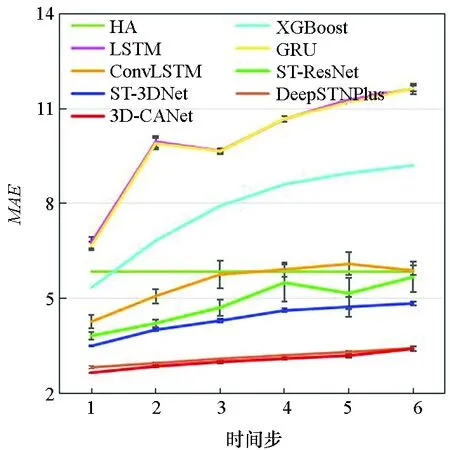
(d) BikeNYC的MAE(d) MAE on BikeNYC
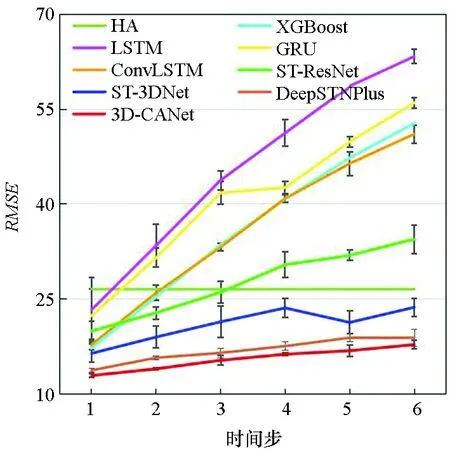
(e) TaxiNYC的RMSE(e) RMSE on TaxiNYC
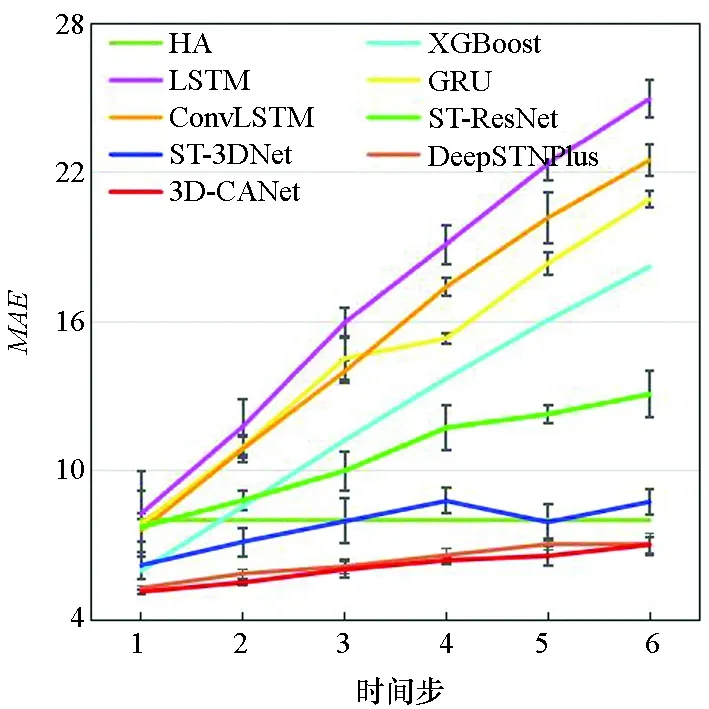
(f) TaxiNYC的MAE(f) MAE on TaxiNYC图7 多步预测结果Fig.7 Multi-step prediction result
3.5.2 通道分组的数量
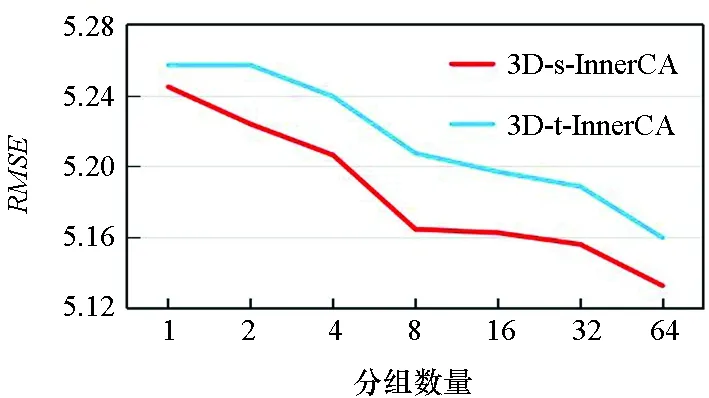
在3D-InnerCA单元中对通道进行分组,从而捕获每组通道内的全局相关性。如图8所示,实验结果表明,组数越多,模型预测的效果越好。因此,将组数设置为最大值,即通道数。这正如同本文的观点,每个通道内的全局相关性都是不同的。
3.6 消融实验
(a) RMSE
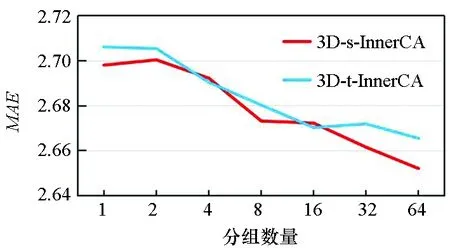
(b) MAE图8 在BikeNYC数据集上不同通道分组数量对3D-s-InnerCA和3D-t-InnerCA的效果Fig.8 Effect of different numbers of groups in 3D-s-InnerCA and 3D-t-InnerCA on BikeNYC
这里通过消融实验来验证模型各组件的效果。在表3中显示3D-CANet模型的每个组件以及它们组合后的效果。3D-Conv模型将3D-CANet模型中3D-InnerCA单元的注意力结构替换为3D卷积,并且用有Cout=2个大小为3×3的卷积核的2D卷积来替代InterCA单元。3D-Conv_InterCA模型在此基础上添加了InterCA单元。通过比较这两个模型,可以发现InterCA单元使模型性能更好。此外,3D-CANet_s和3D-CANet_t模型分别为在3D-InneCA单元中保留时间和空间分支的3D-CANet模型,结果表明仅用3D-s-InnerCA或3D-t-InnerCA都能使预测结果更为准确。当然,同时使用它们时,3D-InnerCA单元的性能达到最佳。总结来说,每个组件都有助于提升3D-CANet模型的预测能力。
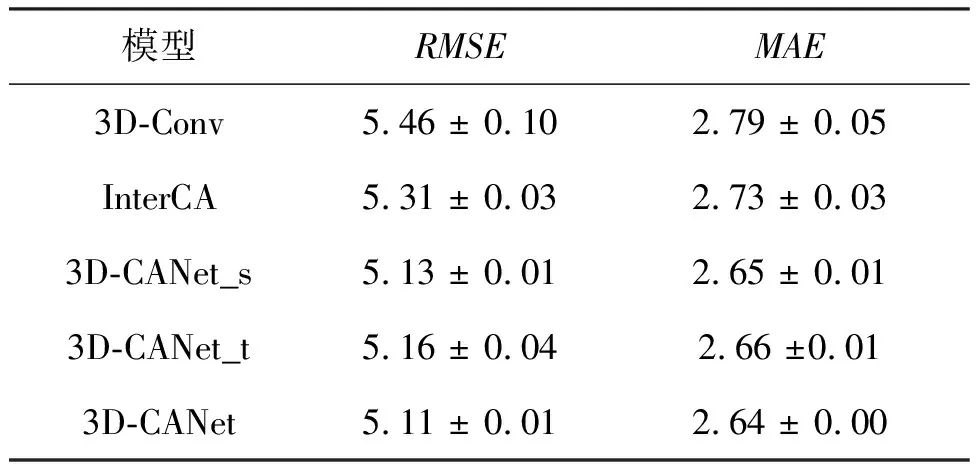
表3 在BikeNYC上的消融实验
4 结论
本文设计用于预测交通栅格流量的时空模型3D-CANet。通过对特征通道进行分组,提出的3D通道内注意力单元从时间和空间两个方面进行注意力计算,动态学习不同特征通道中的全局时空相关性,有效提升了模型的时空建模能力。此外,3D通道间注意力单元能够针对不同特征通道在各个区域上的重要性进行动态学习,提升了模型的表征能力。经过3个交通流量数据集的实验评估,结果表明本文提出的3D-CANet模型性能优于其他8个基准模型。
