强时频无碰撞区跳频序列理论界

许成谦，邢方园，王晓红

(燕山大学 信息科学与工程学院，河北 秦皇岛 066004)

文章编号：1007-791X(2022)03-0257-07

0 引言

扩频通信技术是基于香农公式以扩大带宽的方式来增加信道的容量，其实现方式主要有三种，分别是直接序列扩频、跳频扩频和跳时扩频[1-2]。其中，跳频技术通过一组伪随机码控制频率跳变实现扩频通信，具有低截获概率、较强的抗干扰能力、多址组网能力、抗衰落能力、易于与传统窄带通信系统兼容的优点，因此广泛应用于各种通信系统[3-4]。

跳频通信系统的性能由跳频序列决定，跳频序列的性能用Hamming相关特性来衡量，跳频序列集 ( Frequency Hopping Sequence Set,FHSS)的Hamming相关值受到频隙大小、序列个数、序列长度等参数的限制，这种限制关系称为FHSS的理论界[5]。目前为止，跳频序列在一维无碰撞区(No Hit Zone,NHZ)、低碰撞区周期Hamming相关理论界的研究和序列集的构造已取得了很多成就[6-12]，二维无/低碰撞区周期Hamming相关理论界的研究和构造满足该理论界的序列集也取得了不小的进展[13-15]。

跳频序列的研究主要集中在无/低碰撞区内Hamming相关性分析和构造满足该理论界的FHSS。在信息传输过程中，时延和频移有可能超出无/低碰撞区，故无/低碰撞区外跳频序列集Hamming相关性优化也是至关重要的。Zeng等人在文献[16]中研究了强一维无碰撞区FHSS的构造和性能分析。本文导出了包含频隙个数、序列长度、序列数目、时频二维NHZ之外FHSS最大异相Hamming自相关函数值和最大互相关函数值的理论界。提出了强时频二维无碰撞区FHSS的概念。对一类强时频二维无碰撞区FHSS的Hamming相关性进行了分析。

1 符号和基本概念

(1)

0≤τ≤L-1,0≤υ≤q-1，

其中，i+τ≡(i+τ) modL,i=0,1,…,L-1。当xi=yi+τ+υ时，h(xi,yi+τ+υ)=1；当xi≠yi+τ+υ或yi+τ+υ∉F时，h(xi,yi+τ+υ)=0。

Hxx(τ,υ)称为x的频域非周期移位的时频二维周期Hamming自相关函数。当x≠y时，Hxy(τ,υ)称为x和y的频域非周期移位的时频二维周期Hamming互相关函数。

定义2设频率F={f0,f1,…,fq-1}是大小为q的频率集合，S是F上含有M个周期长度为L的FHSS，TA、VA为非负整数，定义

Zat=max{TA|Hxx(τ,υ)=0，∀x∈S，0≤τ≤TA，0≤υ≤VA，(τ,υ)≠(0,0)}，

Zaf=max{VA|Hxx(τ,υ)=0，∀x∈S，0≤τ≤TA，0≤υ≤VA，(τ,υ)≠(0,0)}，

Zct=max{TA|Hxy(τ,υ)=0，∀x≠y∈S，0≤τ≤TA，0≤υ≤VA}，

Zcf=max{VA|Hxy(τ,υ)=0，∀x≠y∈S，0≤τ≤TA，0≤υ≤VA}，

Znt=min{Zat,Zct}，Znf=min{Zaf,Zcf}，

则[0,Znt]×[0,Znf]称为S的频域非周期移位的时频二维NHZ，[0,Zat]×[0,Zaf]称为S的频域非周期移位的周期Hamming自相关时频二维NHZ，[0,Zct]×[0,Zcf]称为S的频域非周期移位的周期Hamming互相关时频二维NHZ，若S在区域[Znt+1,L-1]×[0,Znf]上进行了Hamming相关性优化，则称S为强时频二维无碰撞区FHSS。

2 强时频二维无碰撞区跳频序列集的理论界

设频率F={f0,f1,…,fq-1}是大小为q的频率集合，S是F上含有M个周期长度为L的跳频序列的序列集，[0,Znt]×[0,Znf]为序列集的NHZ。文中采用以下表示：

Ha(S)=max{Hxx(τ,υ)|(τ,υ)∈[Znt+1,L-1]×[0,Znf]且(τ,υ)≠(0,0),x∈S}，

Hc(S)=max{Hxy(τ,υ)|(τ,υ)∈[Znt+1,L-1]×[0,Znf],x，y∈S,x≠y},

Hm(S)=max{Ha(S)，Hc(S)},

简记Ha=Ha(S)，Hc=Hc(S)，Hm=Hm(S)。

Ha和Hc分别是序列集S在时频二维无碰撞区[0,Znt]×[0,Znf]之外的最大异相周期Hamming自相关和最大周期Hamming互相关。下面导出有关Ha和Hc的理论界。

引理1设频率F={f0,f1,…,fq-1}是大小为q的频率集合，S是F上含有M个周期长度为L的FHSS，任意x,y∈S，对于任意的正整数0≤Znt≤L-1,0≤Znf≤q-1，令函数

(2)

则

(3)

证明对于任意x,y∈S，任意正整数0≤Znt≤L-1,0≤Znf≤q-1，有

Hxy(τ,υ)=

以下将对Znt=0和Znt≠0两种情况分别作出讨论。

情况一：当Znt=0时，即时域上不存在NHZ。

情况二：当Znt≠0时，即时域上存在NHZ。

M(L-Znt)(Znf+1)Ha+
M(M-1)(L-Znt)(Znf+1)Hc。

证毕。

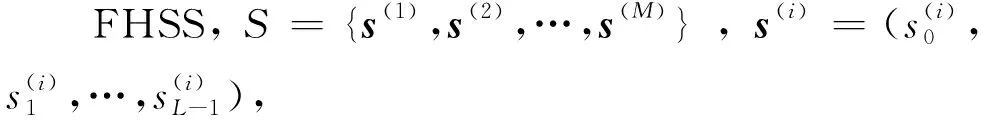
引理2[10]对于任意正整数τ，τ=0,1,…,L-1有

(4)

引理3对于任意正整数Znt和Znf，0≤Znt≤L-1,0≤Znf≤q-1，有

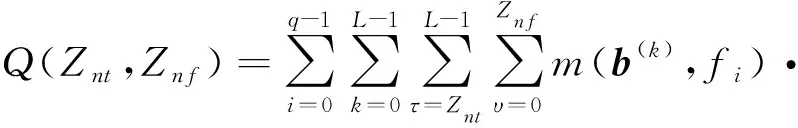
(5)

证明对于任意正整数i=1,2,…,M,τ=1,2,…,L-1,υ=0,1,…,q-1，因为

所以

由于

因此

m(b(k+τ)+υ,fi)，

证毕。

令函数

m(b(k+τ)+υ,fi)，

(6)

引理4对于任意正整数i,0≤i≤q-1，令

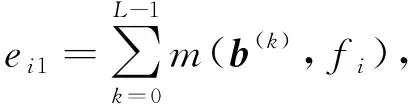
其中k=0,1,…,L-1,则

(7)

证明由等式(6)得

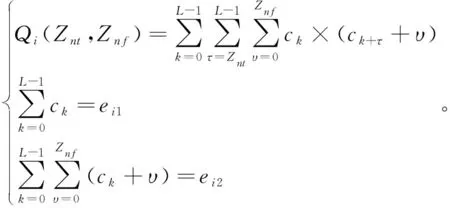
(8)

引理5[11]设g1,g2,…,gq为满足下列等式的正整数

则

(9)

引理6设频率F={f0,f1,…,fq-1}是大小为q的频率集合，S是F上含有M个周期长度为L的FHSS，任意x,y∈S，对于任意的正整数0≤Znt≤L-1,0≤Znf≤q-1，则

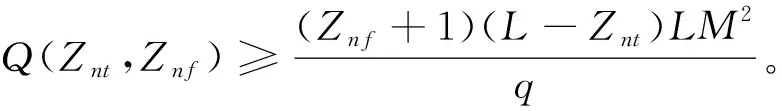
(10)

证明由引理4可知

由引理2可知

根据引理5得

证毕。

定理1设频率F={f0,f1,…,fq-1}是大小为q的频率集合，S是F上含有M个周期长度为L的FHSS，[0,Znt]×[0,Znf]是S的频域非周期移位的时频二维NHZ，时频二维NHZ之外的最大异相周期Hamming自相关为Ha、最大周期Hamming互相关为Hc，对于任意的正整数0≤Znt≤L-1,0≤Znf≤q-1，有：

当Znt=0，即时域上不存在NHZ时，

q(L-1)(Znf+1)Ha+
q(M-1)(Znf+1)LHc≥

(Znf+1)L2M-qL。

当Znt≠0，即时域上存在NHZ时，

q(L-Znt)(Znf+1)Ha+
q(M-1)(L-Znt)·

(Znf+1)Hc≥(Znf+1)(L-Znt)LM。

证明由引理1和引理4得：

当Znt=0，即时域上不存在NHZ时，

ML+M(L-1)(Znf+1)Ha+M(M-1)·

q(L-1)(Znf+1)Ha+q(M-1)·

(Znf+1)LHc≥(Znf+1)L2M-qL。

当Znt≠0，即时域上存在NHZ时，

M(L-Znt)(Znf+1)Ha+M(M-1)(L-Znt)·

q(L-Znt)(Znf+1)Ha+q(M-1)·

(L-Znt)(Znf+1)Hc≥

(Znf+1)(L-Znt)LM。

证毕。

推论1设频率F={f0,f1,…,fq-1}是大小为q的频率集合，S是F上序列数目为M，长度为L的FHSS，[0,Znt]×[0,Znf]是S的频域非周期移位的时频二维NHZ，时频二维NHZ之外的最大异相周期Hamming自相关为Ha、最大周期Hamming互相关为Hc，对于任意的正整数0≤Znt≤L-1,0≤Znf≤q-1，Hm=max{Ha,Hc}，则

当Znt=0，即时域上不存在NHZ时：

当Znt≠0，即时域上存在NHZ时：

证明由定理1得：

当Znt=0，即时域上不存在NHZ时，

q(L-1)(Znf+1)Ha+q(M-1)·

(Znf+1)LHc≥(Znf+1)L2M-qL，

q(L-1)(Znf+1)Hm+q(M-1)·

(Znf+1)LHm≥(Znf+1)L2M-qL，

当Znt≠0，即时域上存在NHZ时，

q(L-Znt)(Znf+1)Ha+q(M-1)(L-Znt)·

(Znf+1)Hc≥(Znf+1)(L-Znt)LM，

q(L-Znt)(Znf+1)Hm+q(M-1)(L-Znt)·

(Znf+1)Hm≥(Znf+1)(L-Znt)LM，

证毕。

令推论1情况一中Znf=0，那么得到FHSS周期Hamming相关理论界。

推论2设频率F={f0,f1,…,fq-1}是频隙大小为q的频率集合，S是F上序列数目为M，长度为L的FHSS，则S的周期Hamming自相关最大旁瓣Ha、周期Hamming互相关峰值Hc和最大周期Hamming相关Hm满足

q(L-1)Ha+q(M-1)LHc≥L2M-qL，

上述结论是Peng、Fan在2004年第一次推导得到的。

3 一类跳频序列强相关性分析

(11)

其中，k=0,1,…,q-1,i=0,1,…,Z。

2) 对于k=0,1,…,q-1，m=0,1,…,L(Z+1)-1取

(12)

其中m=0,1,…,L(Z+1)-1，〈x〉n=xmodn。

定理2上述得到的跳频序列集S具有如下性质：

1) 时频二维NHZ为[0,Z]×[0,N]。

2) 序列长度为(Z+1)L，序列个数为q，时域NHZ边界为Z，频域NHZ边界为N。

3) 时频二维NHZ最大异相自相关值为(Z+1)Ha，最大互相关值为(Z+1)Hc。

证明跳频序列集C={C(i)|i=0,1,…,Z}是不同频率集{F(i)|i=0,1,…,Z}上的FHSS，基于等式(12)可得到序列集S的序列长度为L(Z+1)，序列个数为q。接下来进一步证明序列集S的时频二维NHZ为[0,Z]×[0,N]，基于等式(11)与函数h[x,y]得

(13)

跳频序列集C={C(i)|i=0,1,…,Z}，任意C(i)是满足Peng-Fan界的FHSS，故C(i)最大周期Hamming相关Hm满足Peng-Fan理论界，即

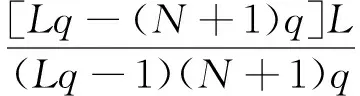
对于(τ,υ)∈[Znt+1,L-1]×[0,Znf]上，接下来分别讨论序列集S的最大异相自相关值和最大互相关值。

1) 最大异相自相关值

考虑Hamming相关函数Hs(k)s(k)(τ,υ)，基于提出的构造方法可得到：

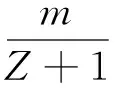
因为跳频序列集C最大异相Hamming自相关为Ha， 对于i=0,1,…,Z有

由此可得序列集S的最大异相自相关为(Z+1)Ha。

2) 最大互相关值

因为跳频序列集C最大Hamming互相关为Hc，对于i=0,1,…,Z有

由此可得序列集S的最大异相自相关为(Z+1)Hc。

跳频序列集C最大Hamming相关Hm=max{Ha,Hc}，通过上述讨论可得出序列集S的最大Hamming相关为(Z+1)Hm，即

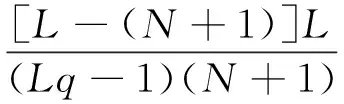
实例：

令Z=2，N=2，F={0，1,2，…，44}，从F中选取F(0)={0，3,6,9,12}共5个频隙，其中任意两个频隙间隔大于等于3，同理得到频率集F(1)={15，18,21,24,27}，F(2)={30，33,36,39,42}。跳频序列集C={C(0),C(1),C(2)}分别从F(0)，F(1)，F(2)上得到的，序列集C具体如下所示：

C(0)={(3,3,6,12,6)；(6,6,9,0,9)；(9,9,12,3,12);

(12,12,0,6,0);(0,0,3,9,3)}，

C(1)={(18,18,21,27,21);(21,21,24,15,24);

(24,24,27,18,27);(27,27,15,21,15)；

(15,15,18,24,18)}，

C(2)={(33,33,36,42,36);(36,36,39,30,39);

(39,39,42,33,42);(42,42,30，36,30)；

(30,30,33,39,33)}，

由等式(12)，得到跳频序列如下所示:

s(0)=(3,18,33,3,18,33,6,21,

36,12,27,42,6,21,36),

s(1)=(6,21,36,6,21,36,9,24,39,

0,15,30,9,24,39)，

s(2)=(9,24,39,9,24,39,12,27,

42,3,18,33,12,27,42)，

s(3)=(12,27,42,12,27,42,0,15，

30,6,21,36,0,15,30)，

s(4)=(0,15,30,0,15,30，3,18,

33,9,24,39,3,18,33)，

令S={s(0),s(1),s(2),s(3),s(4)}，时频二维NHZ为[0,2]×[0,2]，时频二维NHZ外最大周期Hamming自相关Ha(S)=3、互相关Hc(S)=3，最大周期Hamming相关Hm(S)=3。

将涉及的参数代入推导的强时频二维无碰撞区FHSS的频域非周期的时频二维周期Hamming相关理论界中，可知满足该理论界，但不能使等号成立，即不能达到最优，但仍具有很好的相关性能。

4 结论

文中建立了包含频隙个数、序列长度、序列数目、时频二维NHZ之外FHSS最大异相Hamming自相关函值和最大互相关函数值的理论界，给FHSS在时频二维NHZ之外Hamming相关性优化提供标准。提出了强时频二维无碰撞区FHSS的概念。对一类强时频二维无碰撞区FHSS的Hamming相关性进行了分析，该类强时频二维无碰撞区FHSS不是最优的。构造具有最优强时频二维无碰撞区FHSS是进一步需要做的工作。