轨底坡对重载铁路钢轨疲劳裂纹萌生寿命的影响
2022-06-08刘云涛段志东
刘云涛,段志东
(兰州交通大学 土木工程学院,甘肃 兰州730070)
随着我国经济的飞速发展,既有重载铁路使用频次显著提高,钢轨的疲劳裂纹萌生及磨耗问题日益加重,威胁行车安全的同时也带来了巨大的经济损失[1-3]。而轨底坡的设置会影响轮轨间接触状态,不合理的轨底坡参数会提高钢轨萌生裂纹的概率,严重时甚至会威胁行车安全[4-6]。因此对于重载铁路而言,选择更合理的轨底坡参数显得尤为重要。周宇等[7]通过CONTACT程序计算了轮对与内外轨的接触行为,基于临界平面法预测了不同轨底坡数值下曲线线路的疲劳裂纹萌生寿命,对钢轨疲劳寿命进行分析。赵越等[8]通过使用多体动力学软件建立了重载铁路机车和货车车辆的车辆−轨道耦合动力学模型,分析了JM和LM 2种类型的车轮踏面匹配不同轨底坡时,钢轨所受的垂向力。丁军君等[9]基于多体动力学软件建立了钢轨和C80货车模型,分析了不同曲线半径以及不同轨距对车轮磨耗的影响。KIM等[10]以首尔地铁3号线为例,分析了不同的轨底坡参数对列车运行安全的影响。HUR等[11]对比分析了轨底坡分别设置为1:40与1:20时,轮对的等效锥度及钢轨表面的接触状态。高雅等[12]通过多体动力学软件,假设钢轨与列车均为刚体,分析了不同轨底坡数值对地铁运营的影响。钱瑶等[13]对比分析了不同的轨底坡数值对高速铁路轮轨接触状态的影响,找出了LMa,S1002G,XP55与CHN60型钢轨最为匹配的轨底坡数值。LI等[14]利用Archard材料磨耗理论,分析了直线及曲线线路中,设置不同轨底坡参数时钢轨的磨耗情况。以上研究均表明,轨底坡参数以及轮对偏移会对轮轨间接触状态产生影响,与车轮踏面不匹配的轨底坡会导致钢轨表面法向应力过大,影响钢轨的服役期限。因此通过分析轨底坡参数对重载铁路疲劳裂纹萌生寿命的影响,找出更适合重载线路的轨底坡参数,对实际工程应用具有切实意义。本文基于弹塑性接触理论[15],采用双线性随动强化这一本构关系,计算CHN60和CHN75 2种类型钢轨设置不同的轨底坡(1:10,1:20,1:30,1:40,1:50和1:60)时,接触状态以及疲劳裂纹萌生寿命的变化,通过对比得出与钢轨更加匹配的轨底坡类型。同时模拟曲线线路,对轮对设置不同的偏移量,并尝试在曲线线路中设置非对称轨底坡,分析多种非对称轨底坡对轮轨间接触状态以及疲劳裂纹萌生寿命的影响。本研究可为重载铁路轨底坡的设计提供参考。
1 三维有限元模型的构建及验证
1.1 三维轮轨弹塑性模型的构建
基于有限元软件ANSYS建立弹塑性三维轮轨模型,模型由轮对、车轴、钢轨和轨枕组成。通过此模型来模拟分析轮对经过不同轨底坡下的直线线路及曲线线路时,轮轨间的接触状态的变化,并计算其疲劳裂纹萌生寿命。
三维轮轨弹塑性模型如图1所示。整个有限元模型均采用六面体单元,采用CONTA174接触单元和TARGE170目标单元组成的接触对模拟轮轨间的相互作用,钢轨类型为CHN60和CHN75型,钢轨长度为1 500 mm,车轮为LM型踏面车轮,轮对轴重为25 t,车轮半径为430 mm,轨距采用标准轨距1 435 mm,轮对内侧距1 353 mm,轨枕间距为0.6 m,摩擦因数为0.3,通过对轮对施加角速度的方式模拟车轮的滚动,角速度ω为45 rad/s。模型各部分材料参数如表1所示。为了在保证精度的情况下节约计算量,对轮对运动路径上的钢轨以及车轮表面处网格进行加密,模型最小网格尺寸1.5 mm。整个模型总单元数为74.2万个,节点数为271.6万个。

图1 三维弹塑性轮轨有限元模型Fig.1 Three dimensional elastoplastic finite element model of wheel and rail

表1 模型材料参数Table 1 Model material parameters
1.2 模型准确性验证
对不同轴重的轮对经过直线线路过程进行模拟,得出钢轨表面最大接触应力值与文献所得出的结论进行对比[16],对比结果如图2所示。
由图2可知,在同一工况下,仿真结果偏差在5%以内,表明所建立的三维弹塑性轮轨模型准确,可通过此模型来进行下一步分析。

图2 计算结果与前人文献对比Fig.2 Calculated results are compared with the previous literatures
2 疲劳裂纹萌生寿命预测理论
目前普遍采用的疲劳寿命预测模型分为2种方式。一种是MORROW[17]提出的通过物体的疲劳应力曲线对疲劳寿命进行预测,认为金属结构的疲劳寿命可通过S-N曲线进行估算,S-N的曲线表达式为:

式中:S表示金属结构的弯曲应力;N为表金属结构的循环次数;a和b均为实验所得的材料系数。
另一种是JIANG等[18]提出的疲劳裂纹萌生寿命的数学模型,该模型基于应变能与临界平面法提出了一种全新物理量——FP损伤参量,为:

式中:〈σmax〉为疲劳裂纹萌生平面位置的最大法向应力;Δε为疲劳裂纹萌生平面位置处的拉伸应变;Δτ为裂纹萌生平面处的剪应力幅值;Δγ为裂纹萌生平面处剪应变幅值;而j为扭转实验测得,本文取0.2[19-20]。
先通过有限元计算得到钢轨模型各个单元结点的应力分量σij以及应变分量εij,然后通过应力矩阵σ及应变矩阵ε将坐标系转换,可得出任意截面位置的应力应变分量σ′ij和ε′ij。


根据上述公式求得各个节点的损伤参量FP,并找到损伤参量的最大值FPmax,根据公式(7)计算钢轨的疲劳裂纹萌生寿命[21]。

式中:τf为剪切强度系数;G为剪切模量;γ′f为剪切延性系数。参考JIANG等[22-23]的研究,τ取1 015,γ′f取0.509 4,b和c取−0.104 8和−0.550 1。由于较为精准的钢轨屈服应力−循环次数的曲线需要大量实验获得,难度较高,因此本文通过采用JIANG等的损伤参量理论,对不同工况的钢轨疲劳裂纹萌生寿命进行估算,从而分析轨底坡数值对钢轨服役期限的影响。
3 轨底坡对钢轨疲劳裂纹萌生寿命影响分析
3.1 直线线路
对于CHN75轨而言,直线线路不同轨底坡参数下轮轨间接触应力和接触斑如图3所示,最大接触应力和接触斑面积随轨底坡的变化关系见图4。

图3 不同轨底坡CHN75钢轨接触应力分布Fig.3 Contact stress distribution of CHN75 rails on different rail cants

图4 CHN75轨最大接触应力及接触面积随轨底坡的变化Fig.4 Variation of maximum contact stress and contact area of CHN75 rail with rail cants
轨底坡设置为1:10时,轮轨间接触发生在钢轨外侧,接触位置集中在轨距角附近,接触斑形状呈细长椭圆形,接触斑面积为79.5 mm2,接触应力的最大值为1 523.8 MPa。轨底坡为1:20时,接触位置转移至轨顶处附近,轮轨间发生共形接触,接触斑呈带状分布,接触斑面积为139.1 mm2,最大接触应力为899.1 MPa。轨底坡设置为1:30时,接触位置在钢轨内侧,接触斑形状类似于扇形,接触斑面积为121.9 mm2,钢轨表面最大接触应力为1 025.2 MPa。轨底坡设置为1:40时,接触位置在钢轨内侧,接触斑的形状为半圆形,接触斑面积达到109.7 mm2,钢轨表面的最大接触应力为1 219.6 MPa。轨底坡设置为1:50时,接触位置亦在钢轨内侧,接触斑形状类似于菱形,接触斑面积为99.1 mm2,钢轨表面的最大接触应力为1261.3 MPa。轨底坡设置为1:60时,接触位置进一步向钢轨内侧偏移,接触面积进一步缩小,最大接触应力为1 349.0 MPa。
综上所述,CHN75轨设置1:20的轨底坡时车轮与钢轨匹配程度最好,接触位置位于轨顶面正中,接触斑面积最大,接触应力最小。
对于CHN60轨而言,直线线路不同轨底坡参数下轮轨间接触应力和接触斑如图5所示,最大接触压力和接触斑面积随轨底坡的变化关系见图6。

图5 不同轨底坡CHN60轨接触应力分布Fig.5 Contact stress distribution of CHN60 rails on different rail cants

图6 CHN60轨最大接触应力及接触面积随轨底坡的变化Fig.6 Variation of the maximum contact stress and contact area of CHN60 rail with rail cants
轨底坡设置为1:10,轮轨间接触发生在钢轨外侧,接触斑形状呈细长椭圆形,接触斑面积为90.5 mm2,接触应力峰值达到1 317.1 MPa。选用1:20轨底坡时,接触位置在钢轨内侧,接触斑形状为椭圆形,接触斑面积为114.1 mm2,最大接触应力为1 071.0 MPa。轨底坡为1:30时,接触位置在轨顶处,接触斑的形状为椭圆形,接触斑面积为116.6 mm2,最大接触应力为1 230 MPa。当轨底坡设置为1:40时,接触位置同样在轨顶附近,接触斑呈椭圆形,接触斑面积达到121.1 mm2,最大接触应力为1 031.9 MPa。轨底坡的数值设计为1:50时,轮轨间接触发生在钢轨内侧,接触斑面积为106.5 mm2,接触斑呈扇形,接触应力为1 173.9 MPa。轨底坡设置为1:60时,接触位置在钢轨内侧,接触斑形状与轨底坡设置为1:50时类似,接触斑面积为113.1 mm2,最大接触应力为1 105.7 MPa。
综上所述,CHN60钢轨设置1:40轨底坡时,车轮踏面与钢轨的匹配程度最好,接触位置在轨顶附近,接触斑面积最大,接触应力最小。
通过临界平面法计算钢轨的损伤参量,并对不同工况下的钢轨疲劳裂纹寿命进行预测,结果如图7和图8所示。CHN75型钢轨采用1:20这一轨底坡参数时损伤参量最小,为0.485,钢轨可通过轮对的极限次数为3.244 9×106次。CHN60型钢轨设置1:40轨底坡时损伤参量最小,为0.520,钢轨可通过轮对的极限次数2.685 9×106次。因此CHN75轨采用1:20轨底坡、CHN60轨采用1:40轨底坡可延缓钢轨裂纹的萌生,增加钢轨的服役期限。

图7 不同轨底坡时钢轨的损伤参量Fig.7 Damage parameters of rails with different rail cants

图8 不同轨底坡时钢轨可通过轮对的极限通过次数Fig.8 Limit number of rail passes at different rail cants
在2种钢轨均采用合理的轨底坡时,CHN75轨可通过轮对的极限通过次数明显高于CHN60轨,因此设计重载铁路时应尽量选择CHN75型钢轨。
3.2 曲线线路
本文以半径为600 m的曲线线路为例,列车设计时速为55 km/h,外轨超高设计为60 mm,钢轨类型选择更适合重载铁路的CHN75型钢轨,考虑到轮对经过曲线线路时,接触状态区别于直线线路,分析是否存在适当的非对称的轨底坡形式可降低曲线线路的钢轨磨耗。为保证计算精度,在偏移量达到9 mm时对轨距角附近网格进行细化处理,最小网格尺寸为0.4 mm。
钢轨最大接触应力及最大切向应力值随轨底坡参数及偏移量的变化如图9和图10所示,偏移量由0 mm增大至6 mm过程中,内外轨各个轨底坡下的轮轨间接触状态变化很小,钢轨表面最大接触应力同样变化不大。而当偏移量达到9 mm时,外轨表面的接触应力值激增,内轨与车轮的接触状态仍然几乎没有变化。外轨与车轮的接触主要发生在轨距角处,接触面积变小,而内轨与车轮的接触位置仍在轨顶处,接触应力几乎没有变化。最大切向应力值的变化趋势与接触应力值的变化趋势类似,偏移量为0~6 mm时,内外轨均选用1:20的轨底坡参数时,钢轨表面最大接触应力和最大切向应力值最小。在偏移量达到9 mm时,采用外轨设置1:30且内轨设置1:20的非对称轨底坡参数,外轨表面的最大接触应力值和最大切向应力值明显小于其他的组合形式,外轨与内轨表面的最大接触应力分别为1 361.6 MPa和89.8 MPa,最大切向应力分别为338.53 MPa和233.92 MPa。
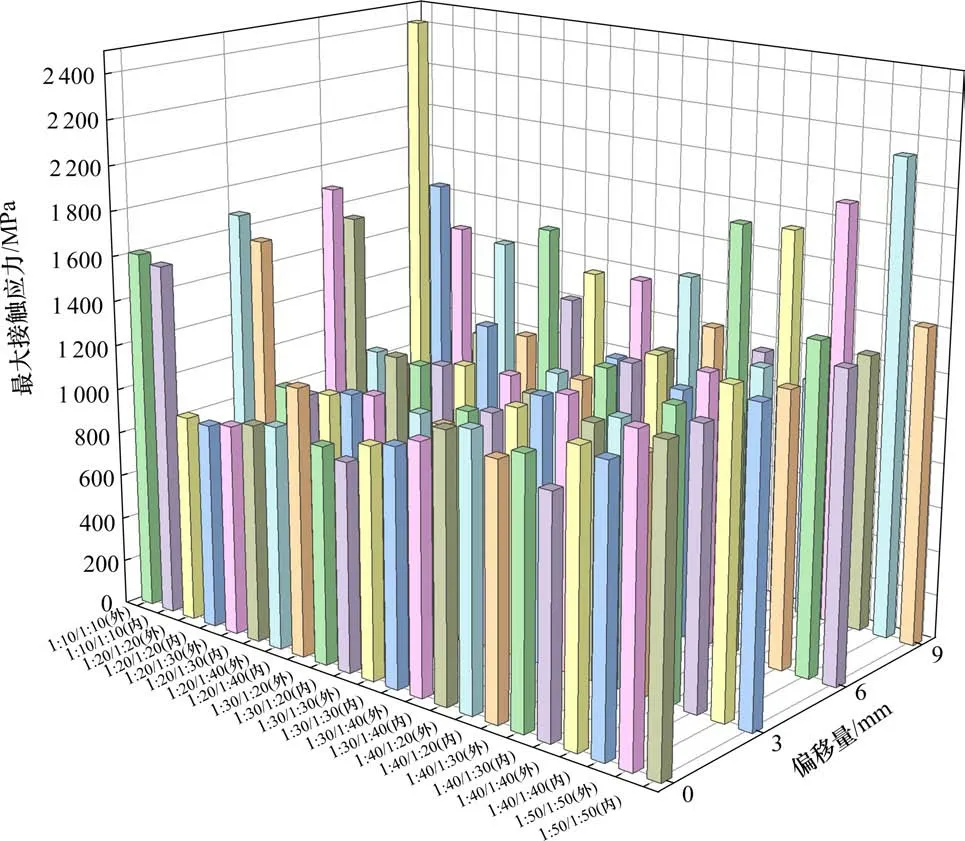
图9 曲线线路钢轨的最大接触应力Fig.9 Maximum contact stress of curved line rail

图10 曲线线路钢轨的最大切向应力Fig.10 Maximum tangential stress of curved line rail
通过临界平面法计算钢轨的损伤参量及疲劳裂纹萌生寿命,结果如图10和图11所示。当偏移量为0~6 mm时,若内外轨均选用1:20的轨底坡参数,钢轨的损伤参量最小,钢轨的疲劳裂纹萌生寿命最长。当偏移量为9 mm时,外轨设置1:30且内轨设置1:20这一轨底坡参数时钢轨的损伤参量最小,分别为0.683(外轨)和0.561(内轨),在使用此种轨底坡组合时,内外轨的可通过轮对次数分别为8.305×105次和3.031×106次。相比于传统的对称设计的轨底坡参数,可有效提高外轨的服役期限。
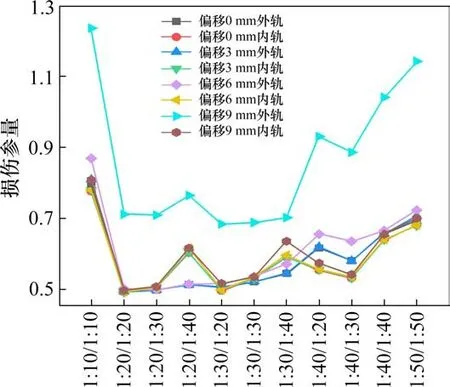
图11 曲线线路钢轨的损伤参量Fig.11 Damage parameters of curved line rail
在轮对偏移量较大的路段,若采用1:30(外轨)和1:20(内轨)这一轨底坡参数,可有效减轻外轨的侧面磨耗,降低疲劳裂纹萌生概率,提高曲线线路运行安全系数的同时也降低了换轨带的经济损失。

图12 曲线线路钢轨可通过轮对的极限次数Fig.12 Limit number of rail passes for curved lines
4 结论
1)在直线线路中,CHN75钢轨采用1:20的轨底坡时,接触斑面积最大,钢轨表面的接触应力值最小,车轮踏面与CHN75钢轨的匹配程度更好,可有效提高钢轨的疲劳裂纹萌生寿命。而CHN60钢轨采用1:40的轨底坡时,钢轨与车轮踏面的匹配程度最好,可有效降低钢轨萌生裂纹的概率,提高钢轨的服役期限。
2)CHN75和CHN60 2种钢轨均采用适当的轨底坡时,CHN75钢轨的疲劳裂纹萌生寿命明显大于CHN60钢轨,因此,重载铁路设计时应尽量选择CHN75钢轨。
3)在曲线线路中,轮对偏移量为0~6 mm时,车轮与外轨间的接触状态几乎没有变化,而当偏移量达到9 mm时外轨表面接触应力激增;车轮与内轨的接触状态在偏移量为0~9 mm区间内始终变化不大。
4)曲线线路中,偏移量在不大于6 mm时,内外轨均选用1:20的轨底坡参数,钢轨萌生疲劳裂纹的概率最低;而当偏移量达到9 mm时,采用1:30(外轨)与1:20(内轨)这一轨底坡参数时,可以降低钢轨萌生疲劳裂纹的概率,有效提高曲线线路钢轨的使用寿命。
