运营状态下新建桥对邻近高铁桥梁沉降的分析

2022-06-08方淑君徐新桐王涛张利勇刘神斌

铁道科学与工程学报 2022年5期

方淑君，徐新桐，王涛，张利勇，刘神斌

(1.中南大学土木工程学院，湖南长沙410075；2.中国联合工程有限公司，浙江杭州310051)

传统的观点认为，造成桥梁基础损坏的主要自然因素是地质水文条件的侵蚀改变；人为因素大多为对靠近桥梁基础的河床开挖及工业污染对土体的影响等[1]。随着城市建设的发展，新建、扩建公路与既有公路铁路桥及埋地管道等交叉或平行的现象已经不可避免[2]，故桥与桥之间的影响也变得不可忽视。就公路桥梁而言，当今超载问题持续性特征明显，而且短期内很难发现桥梁会因此受到影响，一旦后续运维工作不及时，便极易引发诸多安全问题，首当其冲的便是基础的问题[3]。基础的沉降主要是由竖向荷载作用下土层的压缩变形而引起的[4]。研究表明，对于既定的连续刚构桥梁，其基础沉降会导致结构内部产生较大的应力且发生单侧沉降时，最大应力值与沉降值成正比关系。由此可见软土地基上，新建桥梁对既有桥极有可能产生很大的附加沉降从而影响到既有桥的安全和正常使用。一项基于ABAQUES6.14有限元的研究表明，如果桩基础的位移不能满足要求，则可以适当增加土体的硬度和桩的刚度[5]，然而这种做法对于增强既有结构的基础而言很难实现，所以为了确保既有结构的安全，不仅需要控制工程本身的安全风险，还需控制与运营线相互影响引起的安全风险[6]。如果对既有桥梁影响过大，严重的会导致其倾斜、开裂，甚至导致破坏[7]。故邻近既有结构的施工安全评估是一项必不可少的工作[8]。目前研究钻孔灌注桩施工、基坑开挖以及隧道开挖对周边土体变形影响研究较多，而对邻近既有房屋建筑物和线路桥梁结构等影响的研究较少[9]。本文旨在研究讨论新建桥梁在运营状态下对既有桥梁的影响，以既有桥竖向不均匀沉降作为控制标准，寻求与之临近、并行的新建桥运营后对周边土体及建筑的影响范围，从而划定合理的新桥选址区域。既有线路位于珠江三角洲平原地貌区，属西江水系区。根据钻探结果，结合区域地质资料对比分析，各岩层按其成因和时代主要有：人工填土，第四系全新统海陆交相互沉积层，冲积层，残积层，细砂岩以及沙砾岩。其中中间层的第四系全新统海陆交相互沉积层中含有压缩性高、承载力低的软土层。既有线主桥是跨径为55 m+100 m+55 m的刚构桥。新建桥梁由于受到空间及线路限制，与既有桥梁桥墩中心距根据要求需控制在25 m内；且两桥线路夹角小于5°，可认为新旧线路互相平行。新建桥梁为既有线路的扩建线路，桥型布置与基础设计与既存桥梁基本相同。本文就15～35 m的不同间距对旧桥附加沉降量的影响进行建模分析。其中新旧桥群桩基础的几何尺寸及相对位置如图1所示。

图1 新旧桥梁基础位置关系示意图Fig.1 Schematic diagram of relationship between new and old bridge foundations

1 附加沉降对既有桥的影响

1.1 沉降限值

《高速铁路设计规范》(TB 10621—2014)中对墩台在不同沉降类型的沉降限值如表1所示。

1.2 墩台沉降差的影响

按照既有桥的设计图纸，采用有限元分析软件Midas Civil对既有线的三跨预应力混凝土刚构桥进行数值模拟，三维模型如图2所示。

图2 既有线三跨预应力混凝土刚构桥模型Fig.2 Model of existing three span prestressed concrete rigid frame bridge

以仅在一墩上施加10 mm的位移来模拟该桥出现相邻两墩存在不均匀沉降的情况。分析结果显示，同一截面处沉降在底板处产生的应力远大于顶板处；最大弯矩发生在产生沉降的墩梁位置处，且该处的杆端弯矩随边跨的影响最明显[10]。此处给出墩B产生10 mm不均匀沉降时，在全桥各个截面底板处产生的次应力如图3所示。

图3 10 mm桥墩不均匀沉降产生的次应力图Fig.3 Secondary stress caused by uneven settlement of 10 mm pier

既有桥主梁采用C50混凝土，其受拉强度设计值ft=1.80 MPa。由计算可见，相邻桥墩仅10 mm的不均匀沉降产生的附加应力最大值(0.576 MPa)即可占到设计值的32%。由此可见，相邻桥墩之间微量的不均匀沉降即可对运营中的桥梁在结构受力方面产生很大的影响，严重的情况会导致桥梁上部结构造成损伤，如引发桥面的裂缝、承载结构出现问题等[11]。本文在此结合工程实例，就新建桥梁对与之临近的既有桥梁在不均匀沉降方面的影响进行建模讨论。

2 计算建模

2.1 总体模型

有限元计算模型应该要满足空间尺度要求，单桩荷载的轴对称传递分析中，可在水平上的宽度取桩的半径的20～30倍[12]。本文模型以此为参考，取群桩基础外侧的宽度为25倍桩的半径即25 m。有限元模型的范围在竖向取2倍的长桩桩长，本文模型竖向厚度取值为100 m。

在工程实践中需要使用有限元(FEM)或有限差分(FD)分析时，摩尔−库伦强度准则模型现在越来越多地被采用作为经验方法来估算土体的强度及安全问题[13]。而本文模型中的土体与桩基础模型的可靠性，均被使用三维实体单元的实验和工程实践证实。摩尔−库伦(Mohr-Coulomb)强度准则可以较好地描述岩土材料的强度特性和变形破坏行为[14]，同时由于摩尔库伦模型主要适用于单调荷载下如同土壤的以颗粒结构为特征的材料；除此之外的研究结果表明，摩尔−库伦强度准则还可以用来描述透水混凝土的受压性能[15]，可以借此模拟桩基本身的受力情况。而本文中为了区分土体和桩的受力破坏等性质的不同，暂不予采用。因此本文土体采用摩尔库伦模型作为本构模型，桩基础则采用线弹性本构模型。对于土体—桩基础相互作用问题，采用ABAQUS提供的法向和切向的接触关系模拟，法向接触作用(Normal Behavior)采用硬接触(Hard Contact)模拟[16]。

实体单元是几乎能够建造出任意形状、承受任意荷载的模型。本文采用实体单元中可以较为精确计算位移变化的C3D8R(三维8节点减缩积分实体单元)单元。为优化模型的网格划分，本模型选取多个参考面，对结构预先进行划分切割，达到了结构化的划分模型网格的目的。模型网格的划分如图4所示。

图4 网格划分示意图Fig.4 Schematic diagram of grid division

2.2 计算参数

模型中桩基础采用C25，其密度为2 500 kg/m3；弹性模量为30 GPa；泊松比为0.2；既有基础的桩长为40 m，本文模型中新建桥梁的桩长也取40 m进行模拟分析。由于工程实例存在客观的地层变化，需要对性质相近的土体进行合并，本文根据地质报告将土层简化为5层具有代表性的土层，其中第3层弹性模量较小的是对软土层的模拟，各个土层的物理力学计算参数如表2所示。在土体的顶面不设约束为自由边界，在土体侧面设置法向约束，在土体底面设置固定约束。在桩土接触面设置0.35的切向摩擦因数以及法向的硬接触来模拟桩土之间的接触关系。

表2 土层物理力学参数Table 2 Physical and mechanical parameters of soil layer

2.3 计算工况

为切实模拟实际情况中旧桥在运营一段时间后受到新建桥梁的影响，本文模型主要分为5个关键工况，以此为不同的阶段对既有基础的沉降变化进行分析，模拟计算工况步骤如表3所示。

表3 土层物理力学参数Table 3 Physical and mechanical parameters of soil layer

图5 桩基础及地基总体模型图Fig.5 General model drawing of pile foundation and foundation

地应力是地层中未受扰动的天然应力，是地壳应力的统称，天然岩体在特定时空条件下的地应力状态是客观存在的，不能直接推测，只能通过原地测量或者数值模拟确定[17]。为了使数值模拟获得一个存在初始应力，而无初始应变的状态，本文模型采用导入ODB的方法，将模型计算出的应力作为初始应力场导入模型，达到存在应力而无应变的目的，从而更加真实地模拟实际情况中的土层。

3 计算结果及分析

以该工程实例作为研究背景，在不考虑周围既有建筑的情况下，本文单独对新建桥运营状态下对周围环境的影响进行建模分析。由分析结果发现，在距离群桩中心27 m的范围处，地表沉降量依旧可以达到5 mm，可见新建桥会产生范围较远且数值较大的影响。在进行道桥施工过程中，软土地基的不均匀沉降控制尤为重要[18]。由此，本文通过分析该工程实例中土层存在较厚软土层的情况，对近距离内新建桥的建设运营对既有桥产生的不均匀沉降影响做了深入分析探讨。

3.1 新旧基础中心距为20 m时既有桥基础受到的影响

如图6所示，新旧基础中心距x′取20 m时，当新桥进入运营状态后，既有基础桩的沉降受到了新建桥梁的影响产生了附加沉降。具体沉降大小可见沉降剖面云图(图7)。为了探讨新建桥运营后对既有桥的附加沉降影响值，在x′=20时提取1～3号桩的桩顶中心所在直线上的各点处的沉降数据并建立坐标系，1～3号桩处x坐标为20，25，30；新建桩处x坐标为40，45，50(单位：m)。云图表明当新桥进入运营状态后，既有桥的所在位置受到了右侧新建桥梁的影响，即20 m的距离不足以消散掉新建桥梁对周边建筑及土体的影响。

图6 新旧基础中心距为20 m模型剖面图Fig.6 Model section with center distance of 20 m between the new and old foundations

图7 新建桥梁进入运营状态后沉降剖面云图Fig.7 Cloud chart of settlement profile of newly built bridge after entering into operation

3.1.1 既有基础桩所在直线各点的附加沉降分析

桩顶/底-Step3(中部曲线)、桩顶/底-Step5(下部曲线)曲线表示桩顶/底中心连线各点，分别表示当x′=20 m时仅旧桥存在和新桥已经运营这2种情况下的竖向位移。中部曲线与下部曲线的差值即为增加新桥荷载后对各点产生的附加沉降绝对值(上部曲线)，取桩顶/底沉降绝对值z1和z2(单位：mm)，如图8和9所示。

图8 桩顶中心所在直线各点在U3方向上的位移值Fig.8 Displacement values of each point on the straight line of pile top center in U3 direction

当x≤40 m时，z1和z2随x减小而减小，且曲线趋于平缓。在x=40，45，50 m处沉降发生突变为增加新桥荷载后的固结沉降；x=20，25，30 m处未发生突变，说明该处的沉降来自于新建桩的间接影响而非直接荷载的作用。当仅调整x′的值时，图中对应桩土各点的附加沉降量随中心距x′的增大而减小，最后趋于平稳。因此可认为在超过一定范围后，可以忽略新建桩对既有桩基沉降的影响。

3.1.2 既有基础桩顶及桩底附加沉降的比较

为比较研究桩顶与桩底相同平面位置下各点附加沉降量之间的关系，提取桩底中心所在直线上的各点处的沉降数据，作出相同工况下桩底各点位移以及附加沉降量的曲线图如图10所示。

图9 桩底中心所在直线各点在U3方向上的位移值Fig.9 Displacement value of each point on the straight line of pile bottom center is located in U3 direction

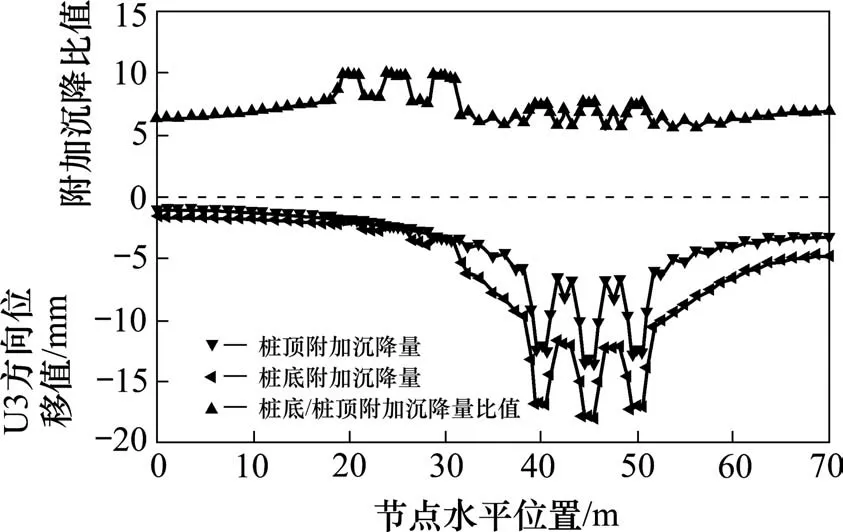
图10 桩顶中心所在平面深40 m和地表处各点附加沉降量比值Fig.10 Ratio of the plane depth of the pile top center 40 m to the additional settlement of each point on the ground surface

桩土各点的附加沉降量与距离新建群桩中心的远近呈现出息息相关的联系，新旧桥基础中心距和既有桥的附加沉降量有着直接关系。

在新旧基础中心距为20 m的模型中，取桩中心所在平面上的一些特征点给出数据如表4所示。

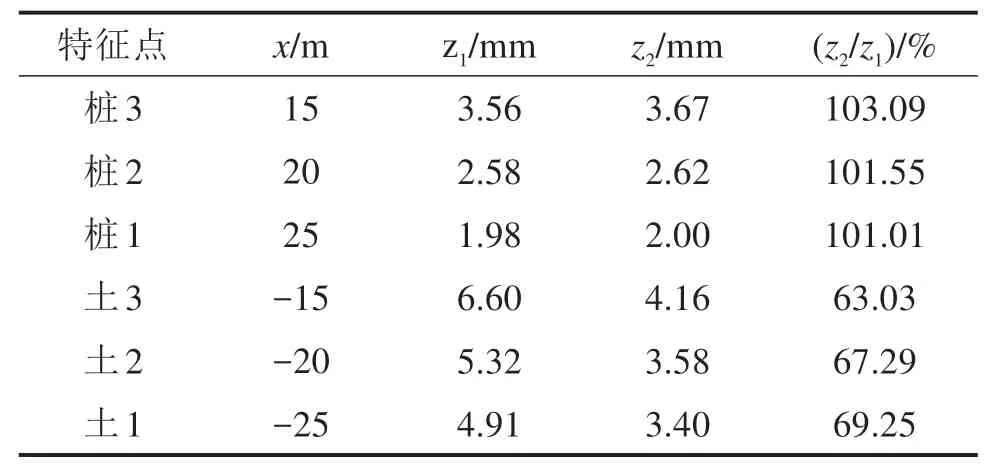
表4 主要特征点处的附加沉降量Table 4 Additional settlement at main characteristic points

3.2 新旧基础中心距大小和既有桥基础受到影响大小的关系

既有桥基础影响受到新建桥荷载的影响和新旧基础的距离影响，在新桩基础同样为40 m时，新旧基础中心间距取15～35 m，每2.5 m间隔为一个模型，共9个模型来探讨距离对旧基础附加沉降量的影响，如图11所示。

图11 不同基础间距下各既有桩桩顶附加沉降量Fig.11 Additional settlement of each existing pile top under different foundation spacing

分别对1，2和3号桩基础的桩顶附加沉降量与新旧基础距离之间的对应数据拟合关系曲线进行分析，可以看出，指数函数与数据点拟合得较好，并且发现将1号桩所在的曲线函数向左平移5 m即为2号桩所在的曲线，向左平移10 m即为3号桩所在的曲线。由此可见既有基础桩顶附加沉降与新建基础在其周边所处的位置有很大关系，并且随着距离的减少呈指数上升的趋势，如表5所示。

由于1，2和3号3根桩基础距离新桥基础距离不同，所以在相同基础中心距x′时，3号桩的桩顶附加沉降量是最大的，3根桩具有沉降差，因此可能导致承台内产生次内力甚至倾覆。

分别对1，2和3号桩基础的桩顶附加沉降量与各桩中心距离之间的对应数据采用最小二乘法拟合。在使用MATLAB对数据进行函数拟合，对比多项式函数与指数函数后，指数函数拟合程度更高，遂使用指数函数进行拟合。各桩的桩顶附加沉降量与该桩至新建群桩中心有关，与既有桩的桩号无关，拟合结果如式(1)所示。

式中：z1为桩顶附加沉降量，m；x0为既有桩与新建群桩中心距离，m，10 m≤x0≤40 m。

非直接作用在既有基础之上的新加荷载在土体中的荷载的影响呈现出指数衰减的趋势。本文工程实例中新桥运营后对既有桥的附加沉降的影响控制在2.0 mm以内，在图中曲线上的新旧基础中心距大于22.5 m后，受到影响最大的1号桩基的桩顶附加沉降量为1.6 mm，且随着距离的增加附加沉降趋于平稳在1.5 mm，故而本工程的新桥基础选位可以由对既有基础的影响作为最大的控制量而基本确定。