电磁轴承冷却优化研究

2022-06-08刘平时振刚刘兴男

轴承 2022年3期

刘平，时振刚，刘兴男

(1.清华大学核能与新能源技术研究院，北京 100084；2.先进核能协同创新中心，北京 100084；3.先进反应堆工程与安全教育部重点实验室，北京 100084)

1 电磁轴承能量损耗

电磁轴承是典型的机电一体化设备，其主要包括控制器、传感器、功率放大器、电磁执行器等部件[1]，通过各个部件之间的协调运行，产生电磁力，支承转子实现悬浮转动。电磁轴承无接触运行，比滚动轴承具有更小的磨损以及更长的寿命，并且能够通过调节控制器参数实现对电磁轴承的主动控制，因此在透平机械、磁悬浮列车等领域得到了广泛应用；但电磁轴承存在潜在的耗能机构：电子元器件的功率损耗、线圈的铜损、电磁轴承的铁损(磁滞损耗和涡流损耗)等[1]，能量耗损产生的热量会加热定转子，进而影响电磁轴承系统的性能。如图1所示，电磁轴承能量主要通过3种形式散失：风损，主要由转子高速旋转产生，尤其是线速度极高的推力轴承圆盘；铁损，主要与电磁感应现象有密切关系，在铁心中磁通密度感应产生涡流，而涡流形成产生损耗的铁心内阻，从而产生损耗[1]；铜损，由于控制电流流经绕组，使线圈电阻发热产生损耗，通常在电磁轴承发热中占据主要地位。

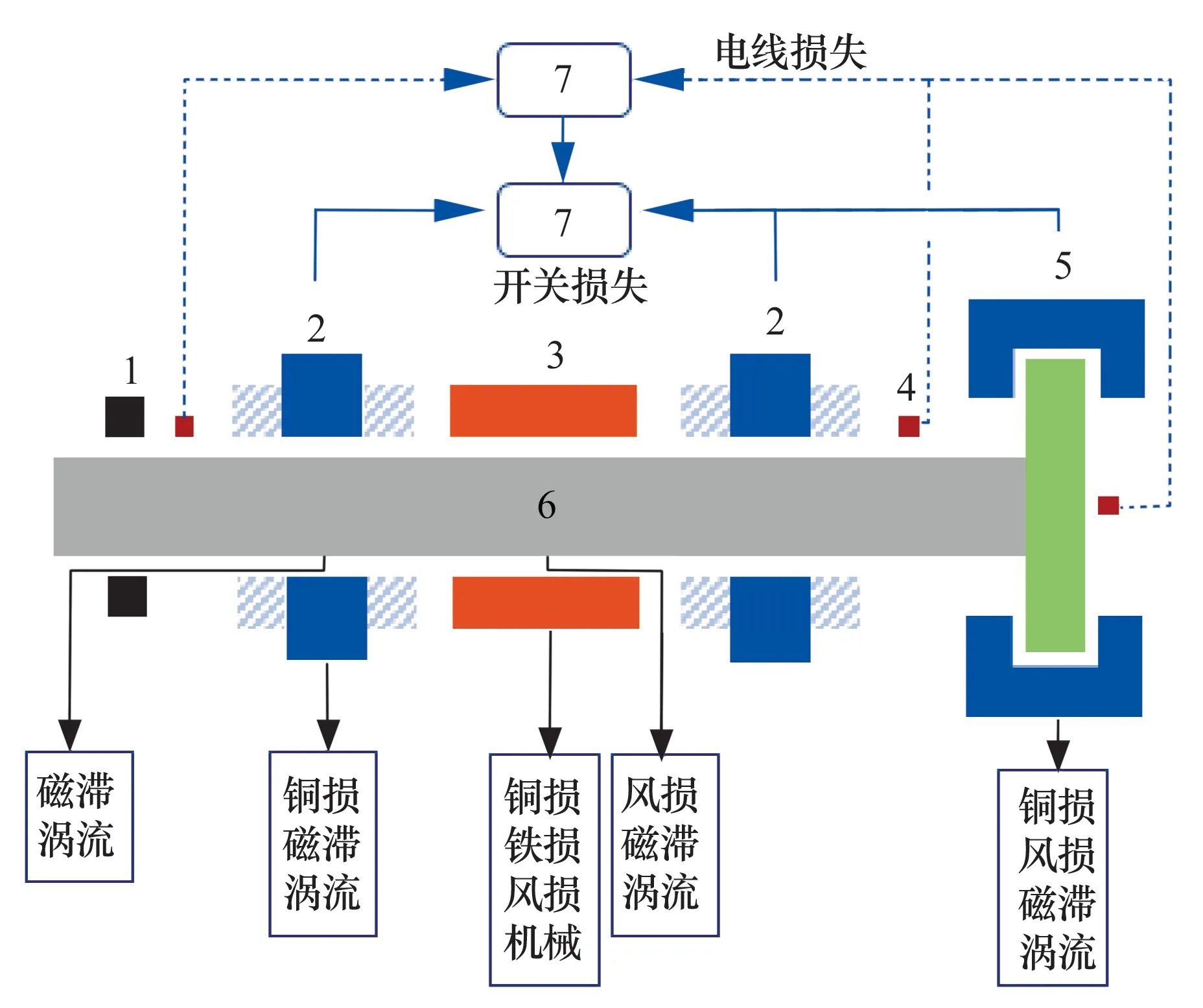
1—保护轴承；2—径向电磁轴承；3—电动机；4—传感器；5—轴向电磁轴承；6—转子；7—控制器；8—功率放大器。

电磁轴承的能量损耗导致了发热，国内外学者针对电磁轴承能量损耗进行了大量的研究：文献[1]研究总结了适用于一维交变磁场磁滞损耗的计算公式；文献[2]对电磁轴承的风损进行了研究，其结论表明风损耗与转速成三次方的关系，尤其是在高转速状态下，风摩擦产生的损耗对电磁轴承发热的影响不可忽略；文献[3]建立了包含涡流、漏磁和边缘效应的磁路模型，完善了电磁轴承能量损耗的模型；文献[4]建立了计算叠片转子涡流损耗的解析方法，通过将电阻功率损耗节分到叠片体积上的方法计算损耗；文献[5]基于涡流制动器的概念，提出了一种新的电磁轴承系统涡流损耗模型，考虑了磁极尺寸、磁极间距等影响，提出了涡流损耗的解析表达式；文献[6]根据磁场强度与磁感应强度之间存在磁滞效应引起的相位差，利用线性系统的条件，得到了单位体积内由于磁滞效应产生的平均损耗；文献[7]建立了高温气冷堆氦气透平直接循环的电磁轴承温度场的物理模型，研究了电磁轴承3种损耗发热模型的计算方法，发现轴向轴承涡流损耗和外边界条件是影响绕组温度的重要因素；文献[8]将电磁轴承涡流损耗视为平均损耗，建立了电磁轴承的温度场；文献[9]通过理论分析电磁轴承温度场的边界条件，建立了轴向电磁轴承的二维温度场模型；文献[10]使用有限元计算的方式，得出了电磁轴承温度分布的数学模型，其在研究中发现二维有限元模型受制于定转子叠片厚度的影响，不能够准确建立磁轴承内部温度场，需要采用三维模型计算；文献[11]对由电磁轴承支承的高速永磁电动机进行了能损分析与热分析，借助外加冷却的方式开展相关研究，但是其研究集中在电动机部分，针对电磁轴承冷却的详细研究并未展开；文献[12]对高温气冷堆电磁轴承冷却系统进行了分析，利用氦冷却代替了蒸汽冷却，由于氦气具有较高的导热系数和热容且密度小，可以建立有效的冷却系统；文献[13]提出研究电磁轴承的发热要考虑电动机发热的影响，开展了对由电磁轴承支承的电动机系统冷却的相关研究，对定子外壳通过外加水套的方式进行散热冷却，但是其研究关注点在电动机散热方面。

目前针对电磁轴承能量损耗的研究大多集中在铁损、铜损、风损这3种形式能量损耗的产生来源以及温度场计算等方面，对于如何进行电磁轴承散热冷却，控制电磁轴承温度的研究较少。因此，本研究围绕轴向电磁轴承开展散热冷却研究，通过外加冷却空气的方式，导出电磁轴承损耗产生的热量。利用不同方案开展冷却试验，并基于有限体积法对冷却优化的电磁轴承进行仿真分析，旨在研究不同冷却方案的冷却能力。

2 冷却试验方案

轴向电磁轴承作为电磁轴承系统中一个关键的部件，其大盘式的结构，加之定转子之间间隙的限制，散热更加困难。其根据运行环境的不同，可以分为开放式和封闭式两种：当处于开放式运行环境时，可以借助周围空气流动吹扫线圈等达到降温的目的；当处于封闭式运行环境时，由于内部结构紧凑、流道复杂，加之定转子间隙太小等因素的制约，使得轴向电磁轴承的有效冷却较为困难,因此本文针对封闭式轴向电磁轴承开展相关冷却优化设计。

冷却试验装置示意图如图2所示，整个试验装置模拟了电磁轴承在仅悬浮状态(不旋转)时的发热情况：采用滚动轴承支承转子模拟电磁轴承悬浮，虽然没有电磁力，但通过机械装配的方式使定转子之间保留悬浮时的间隙；利用定子中的线圈、转子中埋填的发热元件模拟轴向电磁轴承运行时的发热；通过热电偶测量定子温度；单端进气方案均是通过近电动机端端盖的通风口进气，因此用红外探头测量近电动机端推力盘表面温度；端盖上设置有内外两圈通风口，用于冷却介质的进出，靠近轴线的称为内圈通风口，远离轴线的称为外圈通风口；端盖、线圈及定子按照距离电动机的远近进行区分，比如：定子线圈E侧称为近电动机端、F侧称为远电动机端。

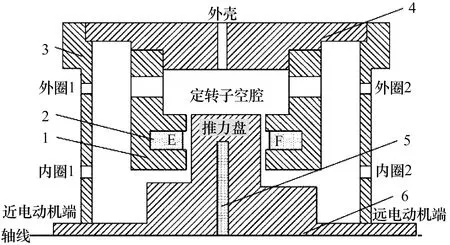
1—定子；2—线圈；3—端盖；4—定子外壳；5—发热元件；6—转子。

试验装置端盖上内外圈各设置了4个进出风口，如图3所示。由于进行的是对比试验，加上冷却空气供给管路的限制，试验时不同通风方案中有一个通风口一直处于封堵状态，即试验时采用的内圈通风口为端盖上内圈1,2中的内Ⅰ、内Ⅱ、内Ⅲ，采用的外圈通风口为端盖上外圈1,2中的外Ⅰ、外Ⅱ、外Ⅲ。

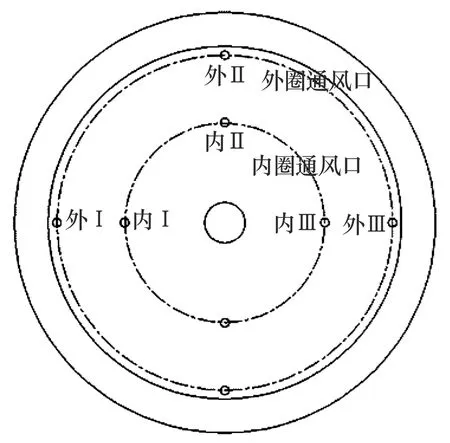
图3 端盖通风口示意图Fig.3 Diagram of ventilator position in cap

根据试验装置中流道的不同，采用的4种冷却方案见表1，即对端盖、定子外壳上的通风口进行不同封堵。

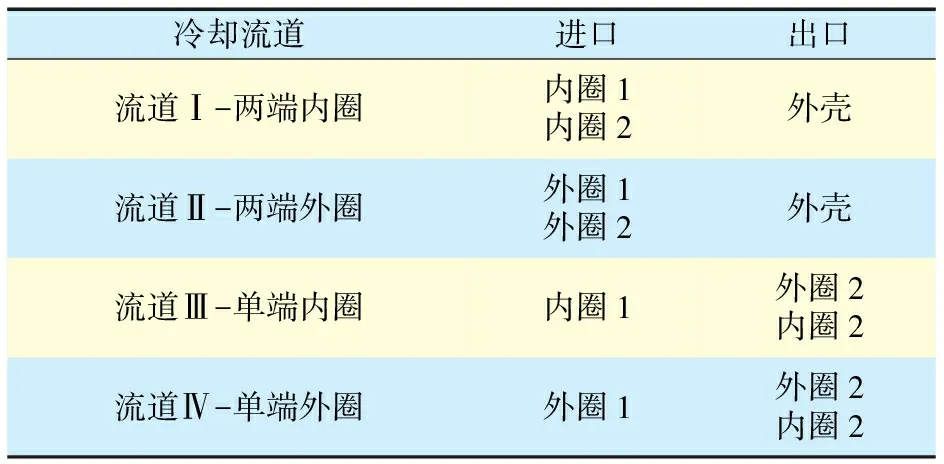
表1 试验方案Tab.1 Experimental scheme

3 仿真计算与分析

3.1 温度场仿真计算原理[14-15]

利用计算流体力学的方法，借助仿真软件ANSYS中的流体仿真工具Fluent，采用控制体积法对冷却试验方案进行仿真分析。

试验中，轴向电磁轴承可以视为圆柱体，故采用圆柱坐标系建立其导热微分方程，进而求解其稳态温度场。图4表示流过微元体表面的热量，为通过圆柱坐标系3个方向的热流量。

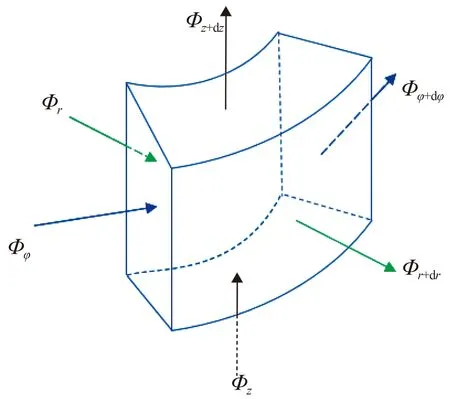
图4 柱面坐标系下微元体导热情况Fig.4 Thermal conduction of microelement incylindrical coordinate system

由能量守恒定律可知流入微元体的热流量为

(1)

式中：λ为物体的导热系数；t为温度。

同时，流出微元体的热量为

(2)

微元体内热力学能Q的变化量ΔQ和微元体的发热量Ψ为

(3)

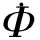
根据电磁轴承的实际工作特性，取固体材料物性为常量，由能量守恒定律，流入微元体内的总热量与微元体内热源的发热量之和等于流出微元体的热量与微元体热力学能的变化量，可得

(4)

冷却方案中涉及冷却介质的流动，因此需要根据输运公式得出描述控制体物理量随时间变化率与净通量之间的关系，即除了能量守恒方程外，本研究还涉及质量守恒方程、动量守恒方程的求解。

实验室条件下的冷却空气均为可压缩流体，因此可得质量守恒方程的变形形式为

(5)

式中：ui为沿着i方向的空气流速。

动量守恒方程表现为有限控制体内流体动量随时间的变化率，等于外界作用在该微元体上的各种力之和，具体表达形式为

(6)

式中：p为静压；τij为应力张量；Fi为外部体积力。

有限体积法得出的离散方程适用于整个计算域的要求条件为：因变量的积分守恒满足任意一组控制体积的要求。因此，可以采用(4)—(6)式对整个试验工况进行有限元分析。

3.2 仿真计算

计算时，采用压力边界条件，即入口压力为 0.1 MPa，采用稳态计算的方法求解温度场与流场。将电磁轴承的涡流、磁滞损耗视为由推力盘发热产生，静态试验忽略风损，将铁损、铜损视为内热源。

试验时，定子线圈由恒流电源提供稳定电流，转子中埋填的发热元件由调压器维持稳定的功率输出。由于定子线圈和转子中发热元件的电阻受到温度升高的影响，试验过程中需微调恒流源与调压器，以维持稳定的功率输出，而微调恒流源与调压器时，设备的输出功率会发生轻微变化。为简化仿真计算中的输入条件，采用积分平均功率计算的方法，即分别计算线圈与转子中发热元件的积分平均功率值，将其作为仿真计算的热源。试验装置发热情况如图5所示，具体模拟的铜损和铁损见表2。

表2 各部分发热功率Tab.2 Heating power of each part

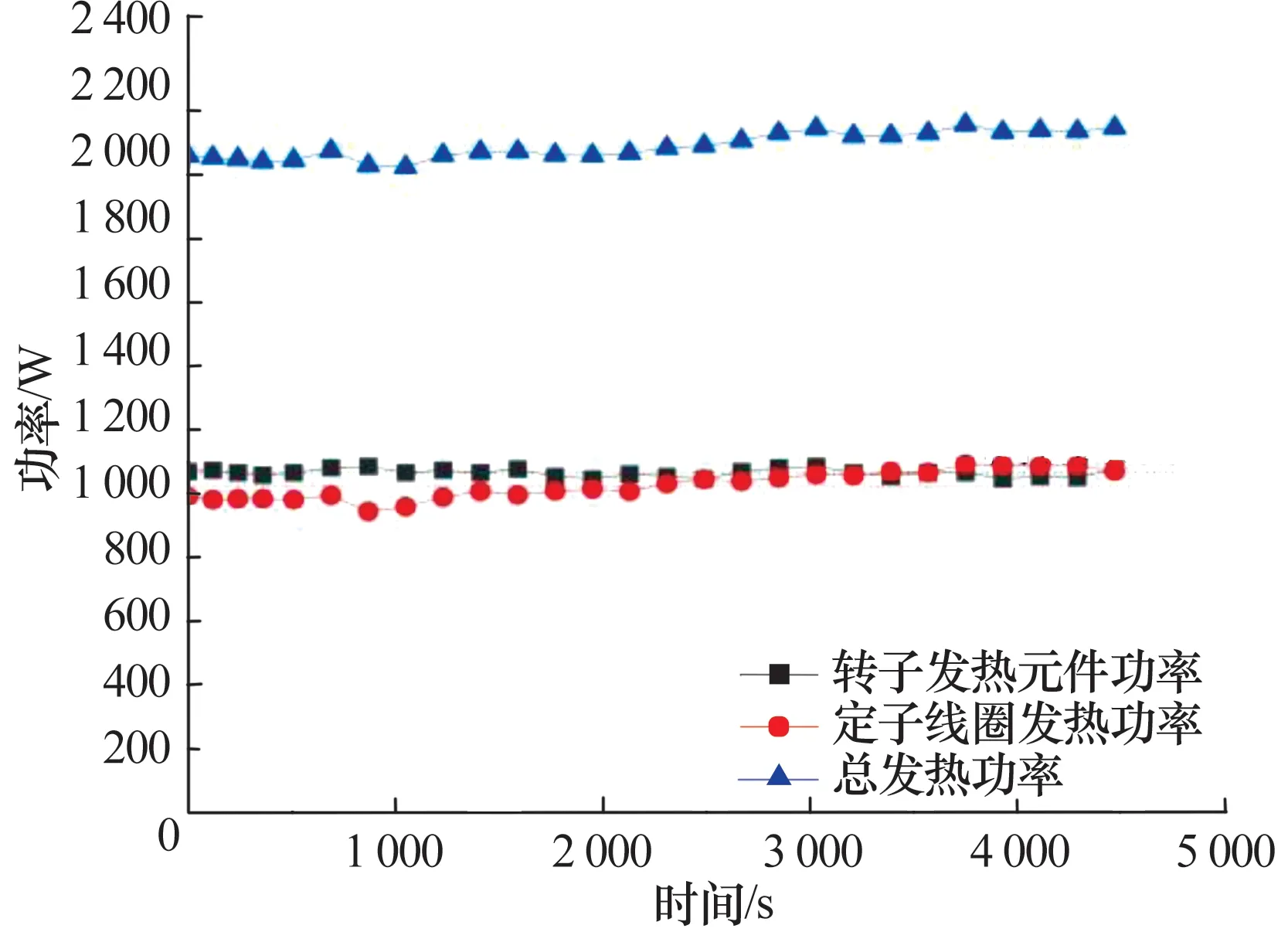
图5 试验装置发热情况Fig.5 Heating condition of experimental device

图6和图7是单端内圈冷却方案的仿真结果，其仿真温度为4个试验方案中最低。从温度场中可以清晰看出，在现有冷却能力之下，线圈和推力盘都能得到有效冷却，达到稳定状态。

图6 单端内圈冷却方案的线圈温度场Fig.6 Coil temperature field of single end innerring cooling scheme

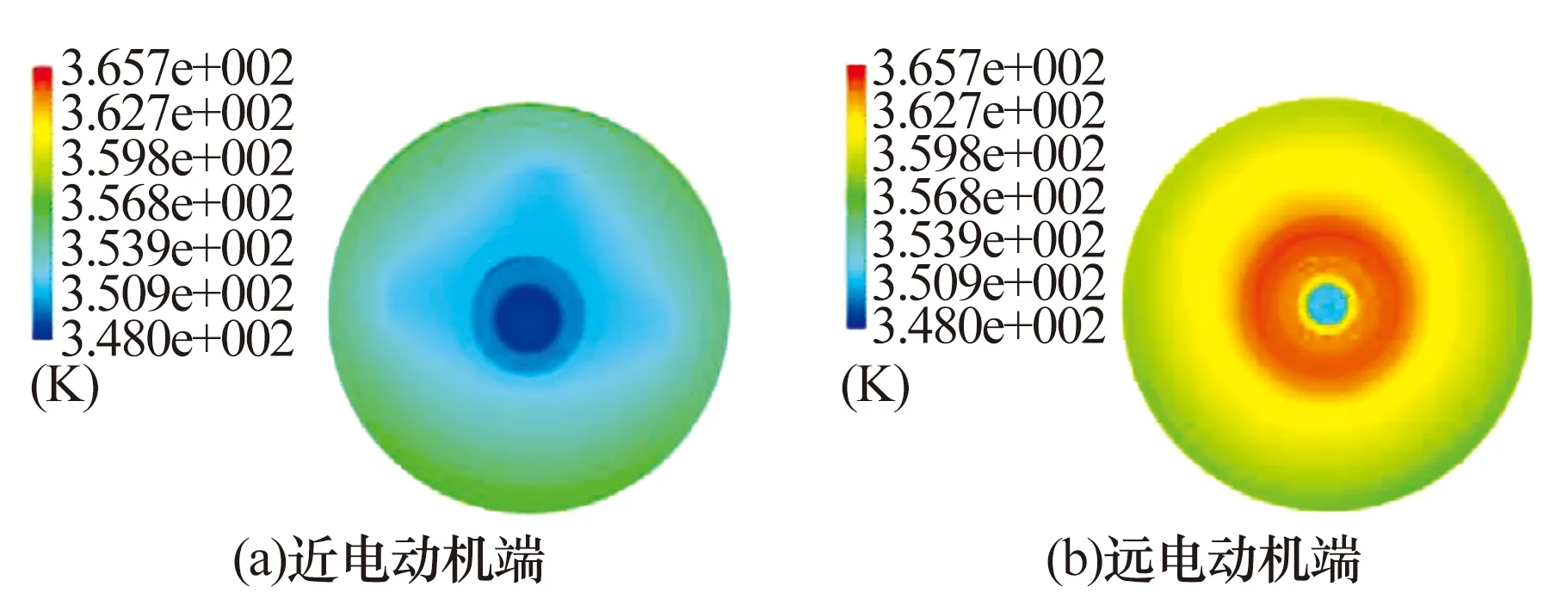
图7 单端内圈冷却方案的推力盘表面温度场Fig.7 Surface temperature field of thrust disc withsingle end inner ring cooling scheme

4 试验分析

试验时，铜损和铁损用定转子的发热功率来模拟，考虑具体某部分的热量，简化试验与分析，关注内部流场以及定转子温度情况，定转子间隙始终为0.7 mm。由于推力盘周向不同测点的温度有差别，需始终保持推力盘停留在同一位置，以减小试验误差。数据分析时均以开启冷却时为时间零点。

4.1 温度分析

图8、图9、图10分别为采用不同流道方案时，近电动机端线圈E、远电动机端线圈F以及推力盘的温度变化曲线。

图8 近电动机端定子线圈E温升曲线Fig.8 Temperature rise curve of stator coil E close to motor

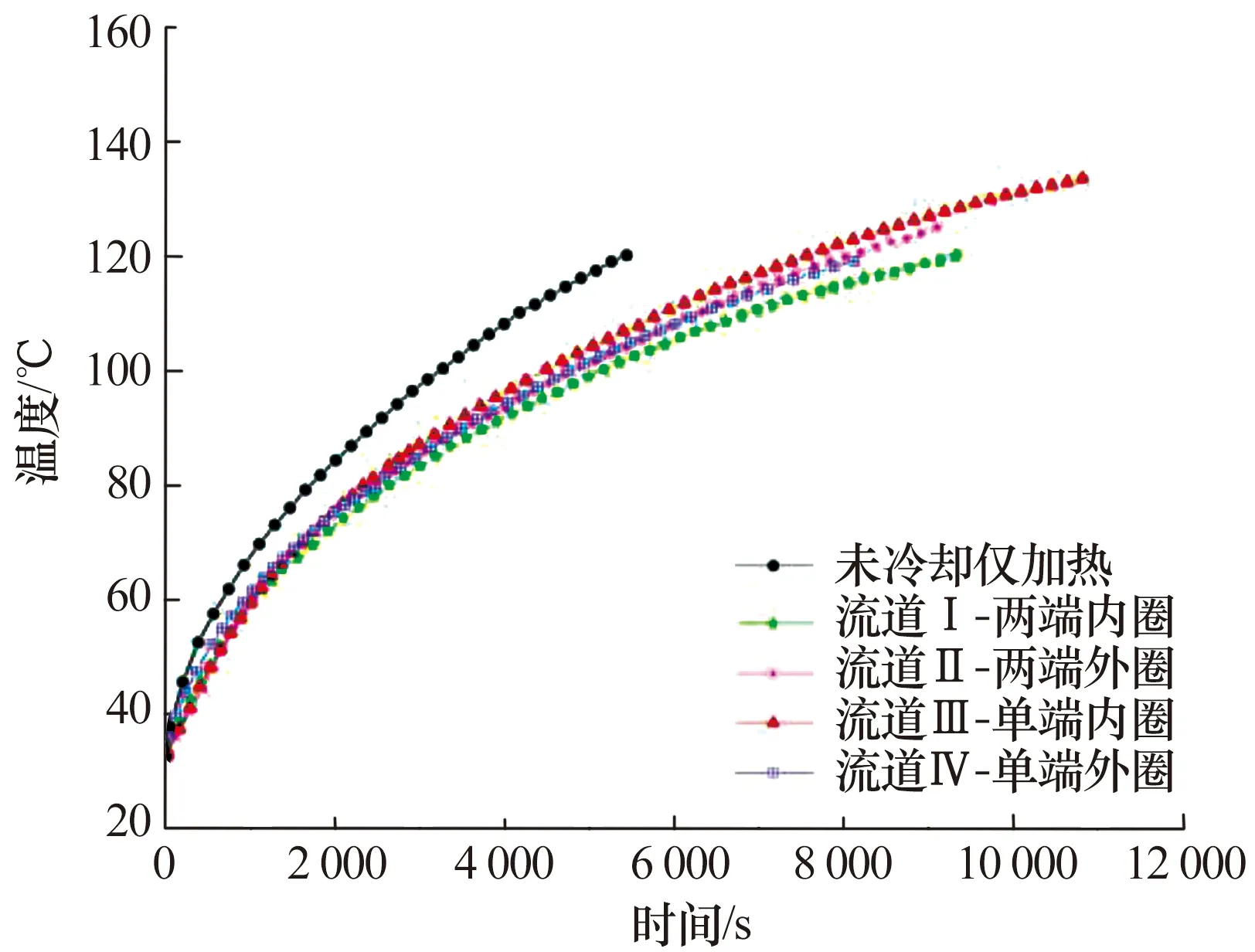
图9 远电动机端定子线圈F温升曲线Fig.9 Temperature rise curve of stator coil Faway from motor

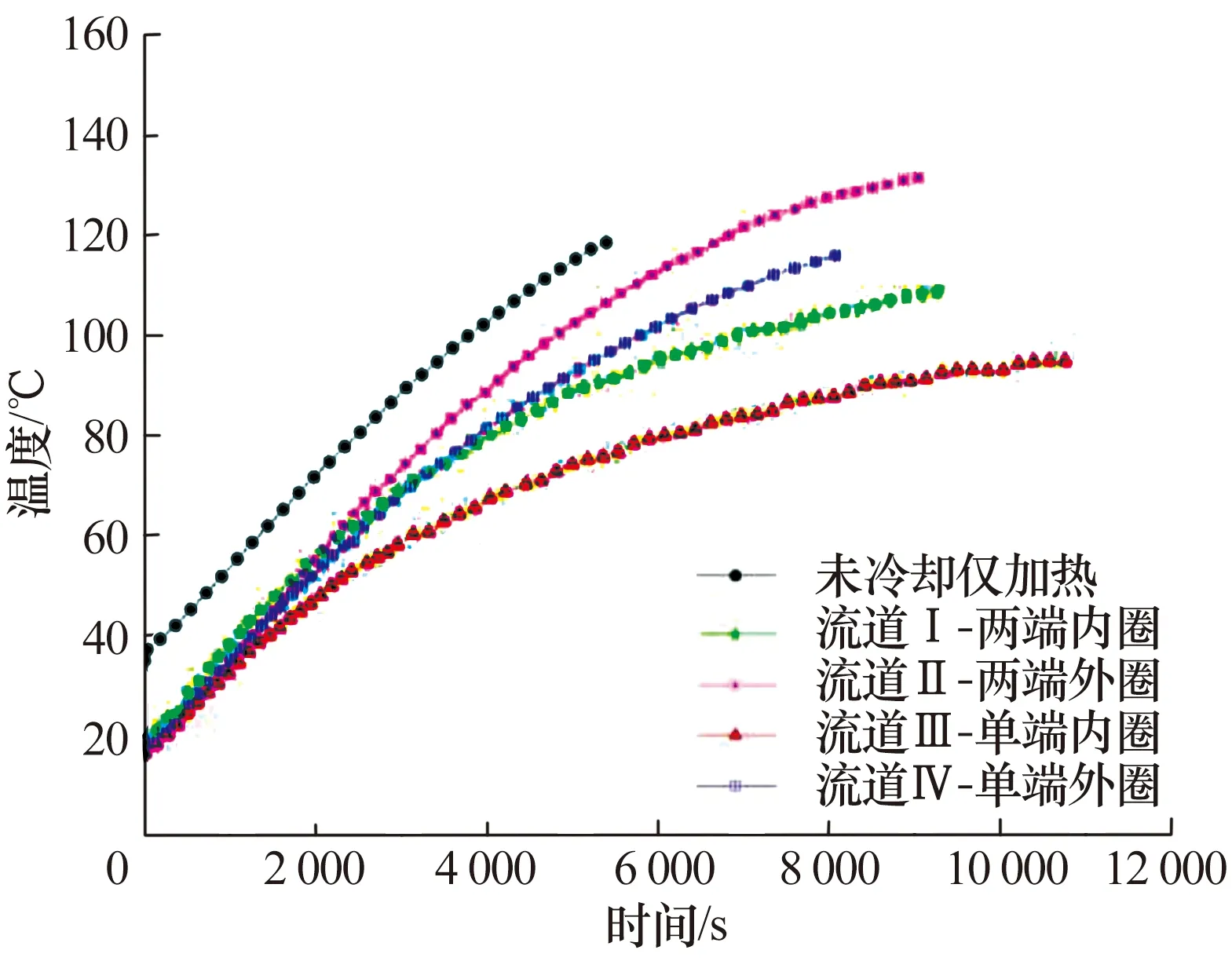
图10 推力盘温升曲线Fig.10 Temperature rise curve of trust disc

由图8可知，试验条件相同时，采用单端内圈(流道Ⅲ)的冷却方案，可以使得近电动机端定子及线圈温升得到有效抑制，而其他3种冷却方案控制温升的效果差异不大。

由图9可知，4种不同冷却方案对于远电动机端定子温升的控制效果差异不大，在试验温升范围之内，4种方案的温度变化趋于一致。

由图10可知，对于推力盘而言，采用单端内圈(流道Ⅲ)的冷却方案，可以有效抑制推力盘温度的升高，而其他3种冷却方案也有抑制作用，但抑制温升的速度较慢。

4.2 流速分析

为分析造成远、近电动机端定子线圈温度变化不一致的原因，通过ANSYS Fluent计算了试验装置内部冷却空气流场，得到如图11所示转子表面流速仿真图。

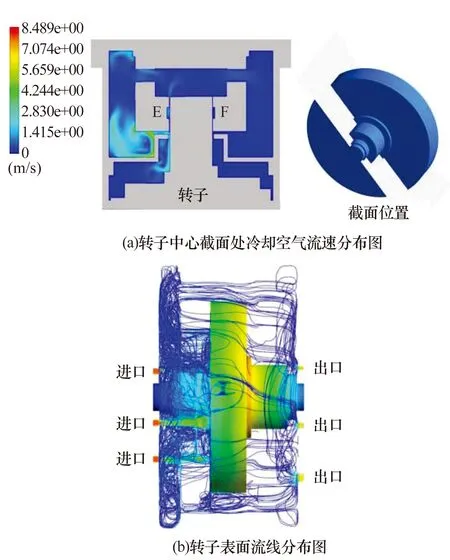
图11 转子表面冷却空气流速仿真图

由图11可知，线圈F侧气隙中的空气流速小于线圈E侧气隙中的流速。在转子悬浮状态下，由于定转子间隙较小，冷却空气在定转子间隙中的沿程阻力损失和局部阻力损失较大(冷却空气进入定转子间隙时，局部压损过大)，导致进入近电动机端(定子线圈E侧)定转子间隙的空气流速小于进口处。同理，当冷却空气经近电动机端定转子气隙、绕过推力盘，流至远电动机端气隙时流速更小，使远电动机端定转子冷却效果不如近电动机端，导致远电动机端的定转子温度较高。