一类集值微分方程解的存在性和稳定性
2022-06-08洪世煌卢靖琦
江 俊,洪世煌,卢靖琦
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
通常通过构造Lyapunov函数来研究微分方程的稳定性,但这种方法并不适用所有问题。当泛函微分方程带有时滞时,Lyapunov函数的构造难度较大,Burton[1-2]的研究成果表明,不动点理论方法在证明稳定性问题中应用更为方便。近年来,不动点方法的应用得到许多学者的关注,获得很多有意义的结果,如Liu等[3-4]用Banach压缩原理证明了一类非线性中立型微分方程全局渐近稳定性;洪世煌等[5]运用不动点方法解决了一类脉冲集值微分方程解的存在性问题。如今,在时标集值微分方程的研究中,也开始运用不动点方法研究方程解的存在性和稳定性[6-11]。受文献[3]和文献[5]的启发,本文研究一类时滞集值微分方程解的存在性和稳定性。
1 预备知识
Kc(Rn)表示Rn中所有非空的紧凸子集构成的集合。定义Kc(Rn)中加法和数乘运算如下:
A+B={a+b|a∈A,b∈B},λA={λa|a∈A}
其中,A,B∈Kc(Rn),λ∈R。在Kc(Rn)上定义Hausdorff距离
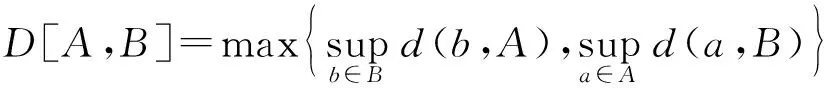
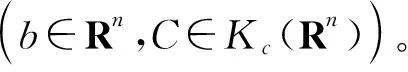

Hausdorff距离满足距离公理,即对任意的A,B,C∈Kc(Rn)及λ∈R,有:
(1)D[A,B]≥0,D[A,B]=0⟺A=B;
(2)D[A,B]=D[B,A];
(3)D[λA,λB]=λD[A,B];
(4)D[A,B]=D[A,C]+D[C,B]。
定义1设A,B∈Kc(Rn),如果存在C∈Kc(Rn)使得A=B+C成立,则称A和B的Hukuhara差(简称H-差)存在,记为C=A-B。
定义2设集值函数F∶I=[t0,T]→Kc(Rn),对于t0∈I,若H-差F(t0+h)-F(t0)和F(t0)-F(t0-h)存在,极限
在Kc(Rn)中的拓扑意义下存在,则称F在t0∈I可导,A为t0处的导数值,A∈Kc(Rn),记为A=DHF(t0)。
定义3给定集值函数F∶I→Kc(Rn),则
(1)若函数f∶I→Kc(Rn)满足对任意t∈I,有f(t)∈F(t),则称f为F的一个选择。SF表示F的所有Bochner可积选择的集合;
(2)假设SF非空,则
称为F的Hukuhara积分。若F的Hukuhara积分存在,则称F可积。
关于集值微分方程的更多概念见文献[6]。
引理1[6]设X∶[a,b]→Kc(Rn)可导,且DHX在[a,b]连续,则

(1)
引理2[6]如果X,Y∶[a,b]→Kc(Rn)可积,则
(2)
本文采用以下记号:

本文将用下述Leray-Schauder不动点定理证明解的存在性。

{u∈X∶∃η∈(0,1),u=ηφ(u)}
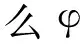
2 主要结果
为了获得非线性时滞微分方程解的稳定性结果,首先给出下列方程解的存在性的充分条件。
(3)
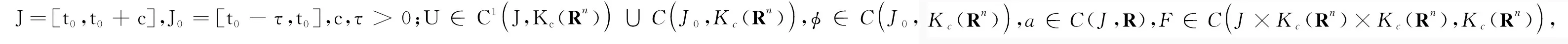
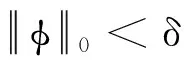
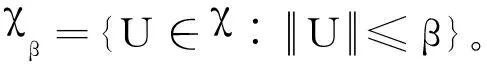
(H2)存在α∈(0,1),使得a(t)≤α。
(H3)对所有X1,Y1,X2,Y2∈χβ,有
(4)
其中,λ1,λ2∈C(J,R+)为单调递增的有界函数。

(5)
显然算子T的不动点即为式(3)的解。为了证明算子T有不动点,需要验证T满足引理3的条件。
首先,证明T在χ1连续。任取U∈χ1,并设序列{Un}⊂χ1收敛到U(n→∞),从而,

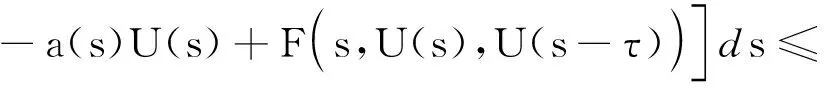

由条件(H1)可知,
所以,
D[T(Un)(t),T(U)(t)]→0(Un→U)
故T在U上连续。

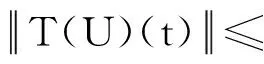
由条件(H3)知λ1,λ2是连续的,所以T(χ2)是有界的。
接下来,证明T是等度连续的。令w1,w2∈[t0,t0+c]且w1 由条件(H3)知λ1,λ2是有界的,设存在N1,N2>0,λ1(t)≤N1,λ2(t)≤N2,t∈[t0,t0+c], 由t的任意性可得: (6) 再由Gronwall不等式可得: 即 (7) 令 (8) rn≤βm (9) 对所有n=1,2,…,成立。另一方面,当n>max{N,βm},由rn的假设,有rn>n≥βm,这与式(9)矛盾,所以集合χ3是有界的。同理,可以证明T(U)(t)=φ(t),当t∈[t0-τ,t0],依然满足定理1的条件。所以,由引理3知,T在χ1存在不动点U1,U1即为式(3)的解。证毕。 接下来证明式(3)的稳定性。 定理2在定理1成立的条件下,若0<αc+υ<1,则可证式(3)的平凡解是局部稳定的。 (10) 所以,有 本文给出了非线性时滞集值微分方程解的存在性的充分条件,并证明解的存在性和稳定性。下一步,计划重点研究非线性中立型时滞集值微分方程解的存在性和集值微分方程的Hyers-Ulam-Rassias稳定性。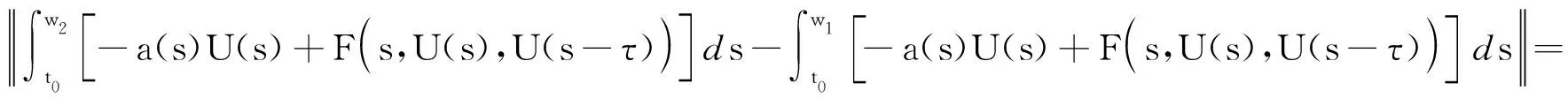


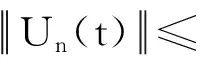
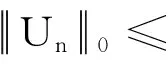
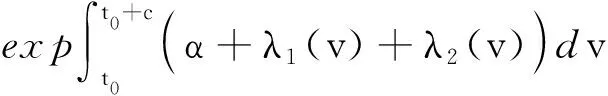

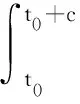
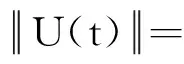

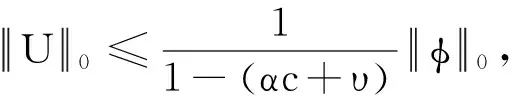
3 结束语
