立管涡激振动流固耦合数值模拟

陈天赐，王瑞金，朱泽飞

(杭州电子科技大学机械工程学院，浙江 杭州 310018)

0 引 言

涡激振动(Vortex Induced Vibration，VIV)是海洋立管结构损伤的主要原因[1]。为了提高海洋资源利用率，衍生出一系列研究VIV的成果[2-8]。研究圆柱结构VIV的主要方法分为实验方法和数值模拟方法，其中数值模拟方法又分为经验模型和计算流体力学(Computational Fluid Dynamics，CFD)。大长径比柔性圆柱结构的VIV响应不同于刚性圆柱体。为了解决CFD全尺度计算耗时及收敛较为困难的问题，部分学者使用二维切片法研究立管的振动响应。王哲等[9]采用OPENFOAM软件把柔性圆柱简化成若干的二维切片代替三维流场，计算时变顶端张力的涡激振动响应，数值模拟结果与实验结果基本吻合。Deng等[10]使用厚切片代替二维薄切片，改进了薄二维切片的局限性，使用RANS湍流模型计算了均匀流和阶梯流下圆柱的振动响应，发现切片厚度为1/50时能满足三维计算的精度要求。大长径比圆柱的涡激振动响应的三维效应明显，切片法无法满足其计算精度的要求。及春宁等[11]运用浸入边界法对处于剪切来流条件下的柔性圆柱进行数值模拟，结果表明剪切率的增大使得流动方向呈现多模态共存现象，其中横向振动模态向一阶模态过渡。Li等[12]使用矢量形式内在有限元法(Vector Form Intrinsic Finite Element，VFIFE)耦合了流向与横向的运动，运用经典范德波方程模拟结构上的脉动流体力，数值模拟结果与实验结果吻合较好，证明了VFIFE法的有效性。Wang等[13]采用任意拉格朗日-欧拉坐标体系处理耦合面动网格，计算均匀来流和剪切来流下垂直立管的VIV响应。Han等[14]使用双向流固耦合分析了立管的振动响应，并成功捕捉到相邻阶振型的转换现象。但是，目前针对脉动流下的涡激振动响应研究甚少，本文采用ANSYS Workbench软件，使用双向流固耦合方法分析柔性立管的涡激振动响应，研究脉动流条件下脉动流频率对立管涡激振动响应的影响。

1 理论分析

1.1 流场求解

先采用有限体积法离散化计算区域，再线性化N-S方程，从而求解获得流场信息。N-S方程是由三大守恒定律推导而来，分别是质量、动量以及能量守恒。因为不涉及能量求解，故本文没有列出能量守恒方程，其余2项守恒控制方程矢量表达如下：

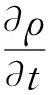
(1)

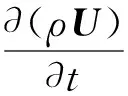
(2)

式中，ρ为流体的密度，U为速度矢量，μ为动力黏度，p为压强，f为单位质量流体体积力的矢量表达形式。

1.2 结构求解

立管单元离散化后，其结构响应控制方程如下：

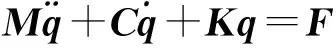
(3)

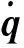
1.3 流固耦合求解

根据求解方式，流固耦合求解的计算可以分为直接求解法和迭代求解法。直接求解法将流场和固体结构的数据信息放在同一个矩阵下进行求解，耗时长且占据计算资源。迭代求解法是分别在流场和结构求解器中进行求解，通过数据交换界面进行插值运算。本文使用分析软件ANSYS Workbench进行计算，其中，Fluent模块用于流场求解，Transient Structural模块用于结构求解，并使用System Coupling模块进行数据交换，最终完成耦合计算，计算原理如图1所示。

图1 流固耦合原理图

2 求解参数设置

2.1 物理模型计算

参考文献[15]的实验参数，本文模拟了两端铰接并受顶端张力作用的PVC材料立管的VIV响应，其材料的物性参数如表1所示。

表1 实验材料物性参数[15]

进行有预应力作用下的模态分析，取前四阶模态分析的频率，并与文献[15]中实验测得的第1阶频率进行对比，结果如表2所示。

表2 模态分析结果 单位：Hz

从表2可以看出，本文第1阶有限元分析结果与文献[15]的误差不大，在接受范围内，说明立管模型的建立较为合理，可用于后续计算。

2.2 求解设置

图2 二维网格平面图

图3 流场整体网格

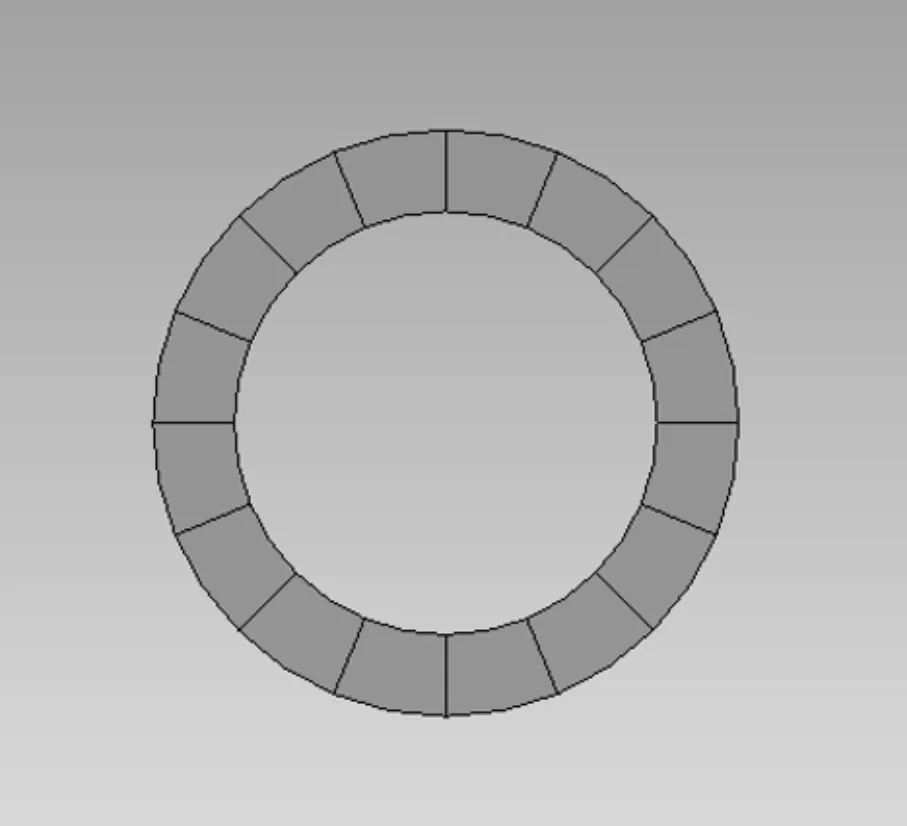
图4 立管结构平面网格

2.3 数值模拟方法验证

选取实验中的一组实验数据进行数值模拟方法验证。顶端张力为60 N，速度为0.15 m/s，实验与数值模拟的振幅数据均为立管中点的振幅数据，纵坐标的y为立管的横向位移，得到的模拟结果与实验结果如图5所示。

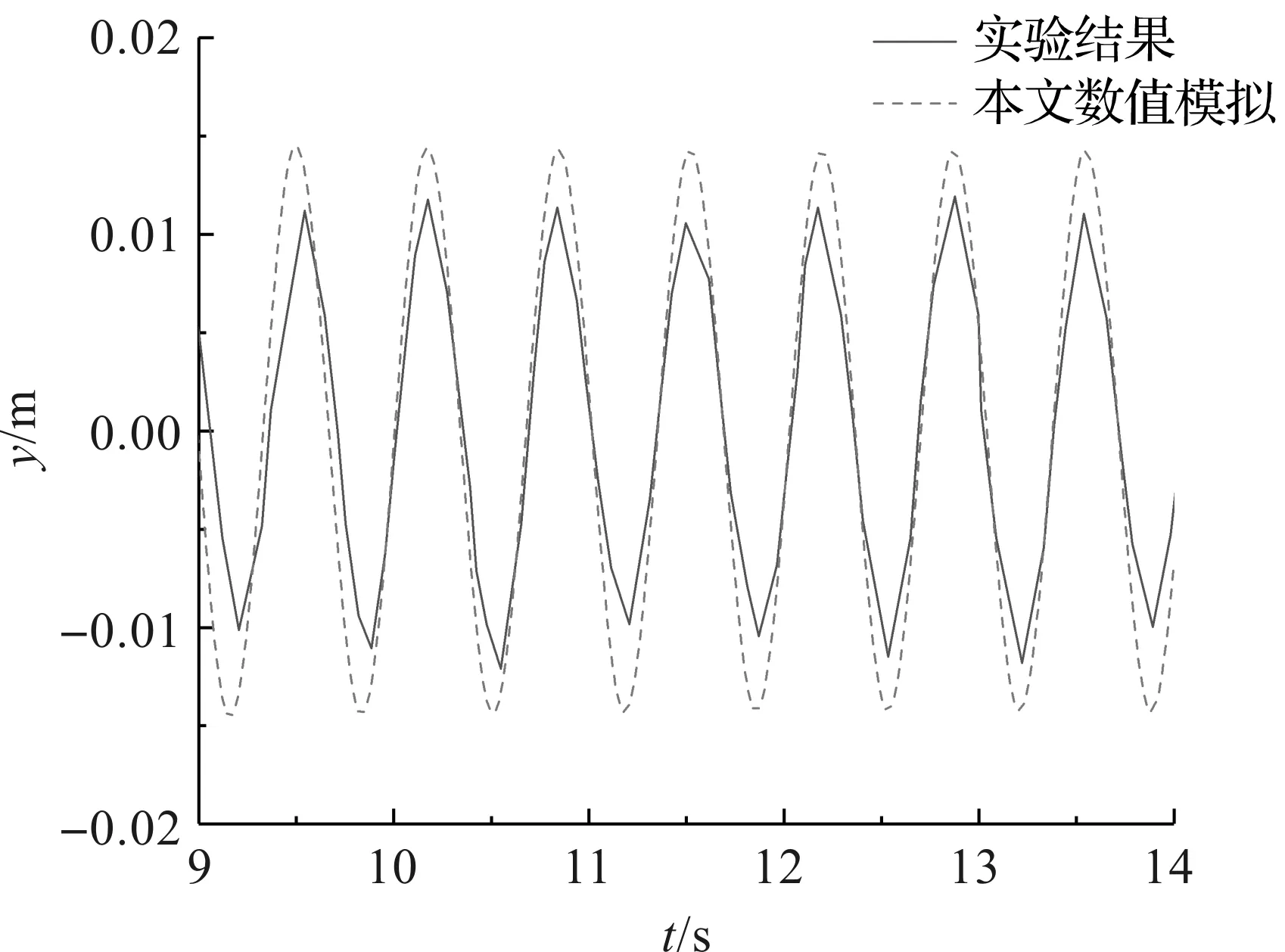
图5 数值模拟和实验结果对比

从图5中可以看出，数值模拟得到的振幅与实验结果的整体趋势十分接近，但最大振幅稍有出入，误差在10%以下，说明仿真结果与实验结果吻合良好，数值模拟方法正确可行。

2.4 脉动来流速度入口设置

目前，立管涡激振动响应的相关研究多是在均匀来流下进行的，脉动来流下的涡激振动响应研究比较少。由于海浪的影响，流动具有强烈的不稳定性，所以不能只考虑定常流动。为此，本文将这种不稳定来流简化为正弦脉动变化形式，研究脉动频率对涡激振动的影响。脉动来流的具体数学表达式[16]为：

(4)

式中，umax为流速最大值，Am为脉动振幅，f为脉动频率，t为时间。

本文的数值模拟实验主要研究脉动频率对涡激振动的影响，故不考虑其余参数。参数设置如下：umax=0.25 m/s，Am=0.2，f分别取0.5fn，fn，2fn，3fn，其中fn为一阶固有频率，根据本文有限元分析结果，其值为3.18 Hz，顶端张力为260 N。

3 数值模拟结果与分析

3.1 立管振动响应分析

3.1.1 水动力系数分析

阻力系数CD和升力系数CL是描述结构受周期性力的2个无量纲参数，分别代表物体流向与横向的受力情况。

(5)

(6)

式中，Fx，Fy分别为流向力和横向力，A为特征长度，本文是指立管的最大迎风横截面积。

不同脉动频率下的阻力系数和升力系数的时间历程曲线如图6所示。

从图6(a)可以看出，脉动频率为固有频率的2倍时，平均阻力系数最大且波动最为明显。当脉动频率低于此值时，脉动频率越低，平均阻力系数越低。脉动频率为固有频率的3倍时，平均阻力系数开始下降，并出现负值，这是由于过高的脉动频率导致立管在回流作用下产生明显的回弹效应。不管脉动频率怎么变化，其阻力系数的波动频率与脉动频率的变化趋势是对应的。从图6(b)可以看出，升力系数的幅值随脉动频率的增大而增大，当脉动频率增大到固有频率的2倍及其以上时，升力系数幅值基本不变，唯一区别是，不同脉动频率达到稳定所需时间的不同。综上分析可以推断，存在一种临界脉动频率，在此之前，阻力系数与升力系数不断提高，一旦过了此临界脉动频率，阻力系数开始下降，但升力系数幅值却开始保持稳定。

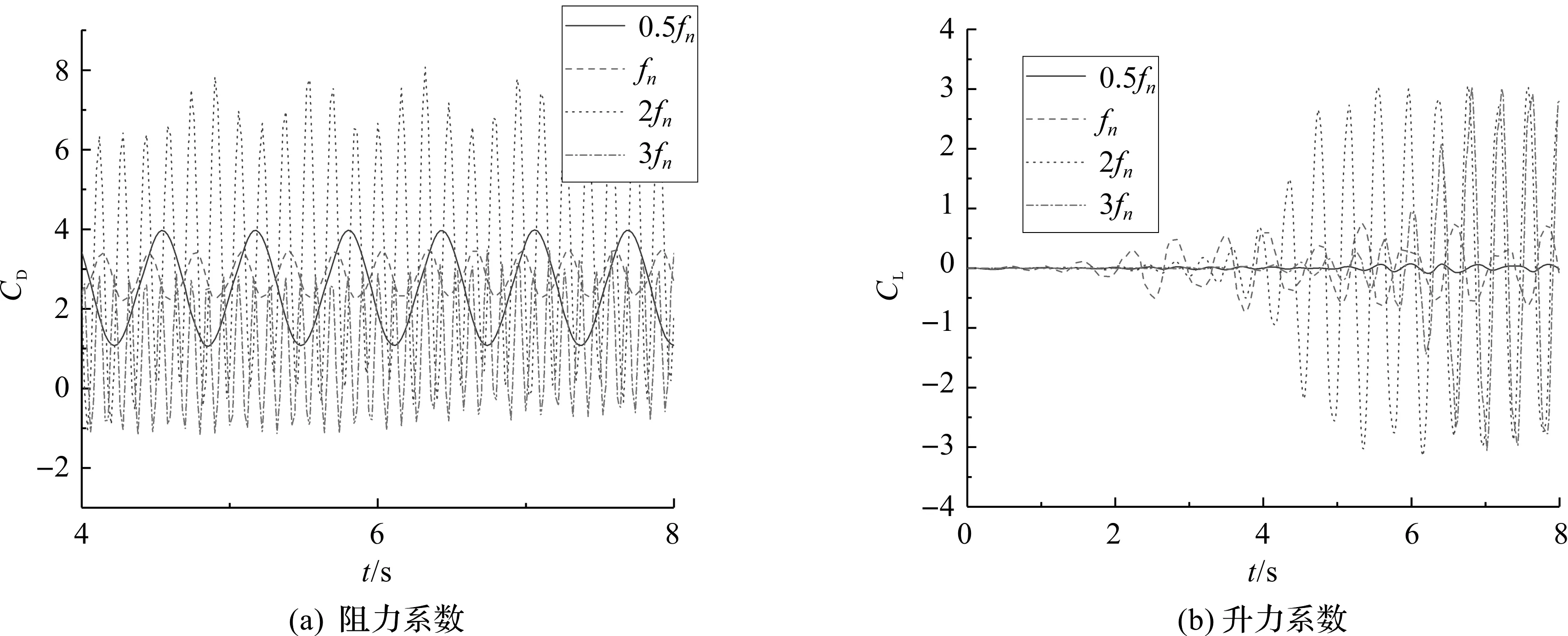
图6 不同脉动频率下的水动力系数

3.1.2 振幅响应分析

振幅均方根(Root Mean Square，RMS)反映立管振动的偏离程度。在立管的轴向Z上，脉动频率分别为3fn，2fn,fn，0.5fn时，不同位置的横向振幅RMS值如图7所示。

图7 不同脉动频率下横向振幅RMS值

从图7可以看出，在立管的轴向长度Z上，振幅均方根最大值出现在中间位置，越靠近两端，其结果越小。如果流动不是均匀来流而是正弦脉动波动，则会降低振幅响应幅值。在4种脉动频率中，脉动频率f为2fn时的振幅结果最大，其次是3fn，fn，0.5fn。在立管轴向长度0.6 m，1.2 m，1.8 m，2.4 m以及3.0 m处分别设置测点1，2，3，4以及5，监测横向振动，横向无量纲振幅用y/D表示，其中D为立管直径。4种脉动频率下，振幅变化曲线如图8所示。由于测点2和测点4，测点1和测点5呈现对称趋势，图8只给出立管在测点1、测点2以及测点3横向振幅的时间历程曲线。

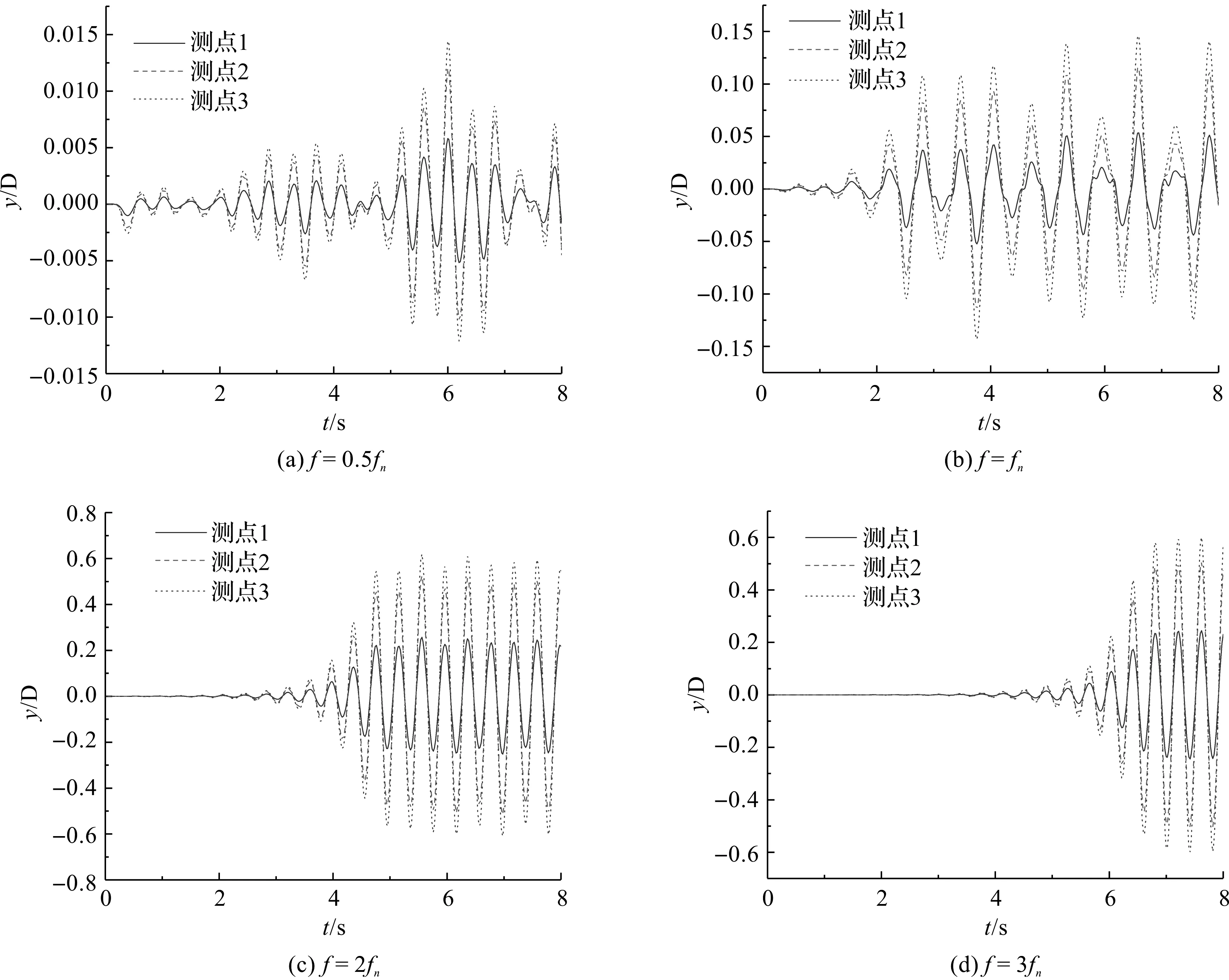
图8 不同脉动频率下立管横向振幅曲线

从图8可以看出，图8(a)和图8(b)中的振幅曲线极其不规则，并且横向振幅也较低，其最大振幅比是脉动频率为0.5fn时的10倍；脉动频率为2fn或3fn时，振幅可以达到立管直径的0.6倍。

对不同的振幅曲线进行快速傅里叶变换(Fast Fourier Transform，FFT)分析振动频率。不同脉动频率下，横向与流向振动频率功率谱密度(Power Spectral Density，PSD)分析结果如图9所示，左侧是横向振动频率分析，右侧是流向振动频率分析。

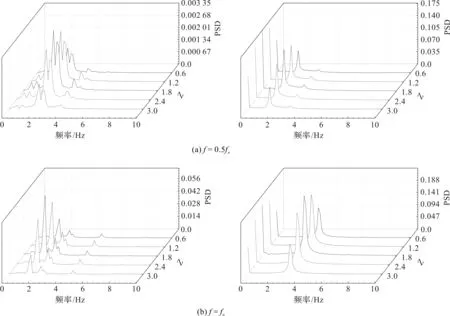
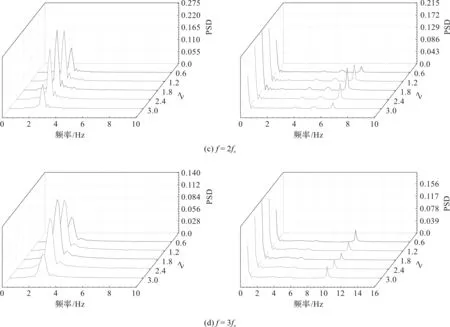
图9 不同脉动频率下振幅FFT变换

从图9(a)可以看出，横向功率谱密度图出现多峰现象，脉动频率与一阶固有频率共存，但脉动频率占绝大部分；对比流向频率可以发现，流向振动主频率并不是横向振动频率的2倍，这和均匀流的结果有差异，也说明分析脉动流条件的必要性。从图9(b)可以看出，横向振动频率也出现多峰值现象，说明此时振动比较复杂且并未稳定。对比图9(c)和图9(d)发现，两者的横向振动频率都接近一阶固有频率，但图9(d)的流向振动频率要大于图9(c)。综上分析可以得出结论，当脉动频率低于fn时，脉动频率对横向振动频率的影响更为强烈；当脉动频率大于等于2fn时，脉动频率对横向振动频率的影响开始减弱，流向振动频率与横向振动频率之比并不完全接近2，脉动频率的增加导致流向的振动频率一直在增加。

3.2 流场分析

文献[5]指出，漩涡脱落在不同的振幅响应分支内具有不同的脱落模式，分别是2S，P+S，2P模式等。2S模式下，每过半个周期，从圆柱的两侧释放1个漩涡；P+S模式下，每过半个周期，圆柱从一侧释放1个漩涡，另一侧则释放1对漩涡；2P模式下，每过半个周期，从圆柱两侧释放1对漩涡，并且2个漩涡强度大小不一。图10给出了不同脉动频率下中间平面在耦合计算第8 s的涡量云图。

图10 不同脉动频率下的涡量云图

图10(a)中，由于脉动频率较小，两侧各存在1个漩涡，且并没有交替脱落，为较弱的2S模式。图10(b)为交替脱落的2S模式。从图10(c)和图10(d)可以看出，当脉动频率大于或等于2fn时，圆柱的偏移距初始位置较大，在两侧分别有脱落的1对漩涡，为2P模式。结合3.1.2节对振幅的分析可知，脉动来流下尾涡脱落模式受到振幅的影响较大。

4 结束语

本文通过模拟脉动来流下的三维立管涡激振动响应，探究了脉动频率对振动振幅及水动力系数的影响，为立管设计与安全寿命研究提供一定的参考。研究结果发现，脉动频率可以降低涡激振动响应；流向振动频率随脉动频率的增大而增大，说明不能忽略脉动流情况下的流向振动。由于计算资源有限，本文只是将海洋波动近似为正弦脉动，与实际的海洋流动有一定出入，后续将研究更为复杂来流形式下立管的涡激振动响应。