基于变分贝叶斯推断的因子分析法
2022-06-08巴丽伟童常青
巴丽伟,童常青
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
因子分析(Factor Analysis,FA)是对高维数据建模分析的重要方法,通过对高维观测数据降维,用少数几个不相关的综合指标来表示多个实测变量,通常用于行为科学、社会科学、市场营销、产品管理等领域,在机器学习领域应用广泛[1]。岳博等[2]使用期望最大化算法(Expectation Maximization,EM)进行因子分析,运用最大似然估计得到模型参数计量,但未考虑模型的复杂性,容易陷入局部最大值。为了克服这些问题,Mayekaw[3]引入贝叶斯理论进行因子分析,使用EM算法找到参数的点估计并作为后验分布的边际分布,但无法证明所使用的EM算法是收敛的。实际模型中很难通过贝叶斯理论估计模型的参数,无法得到精确解,一般采用近似解去近似精确解。Blei等[4]将近似解的求解方式分为随机近似方法和确定性近似方法,一般情况下,确定性近似方法比随机近似方法更容易收敛。变分贝叶斯推断算法是一种确定性近似方法,类似于EM算法,在求解概率模型中有着广泛的应用。
Ghahramani等[5]给出了混合因子分析的变分贝叶斯推断算法,从贝叶斯角度估计模型参数,解决了聚类问题和局部维数减少问题。Wei等[1]从贝叶斯角度进行混合公因子分析,提出公因子分析的贝叶斯混合模型,并结合变分贝叶斯推断算法,对高维合成数据聚类,最后使用贝叶斯信息准则(Bayes Information Criterion,BIC)进行模型选择。变分贝叶斯信息准则(Variational Bayes Information Criterion,VBIC)[6]是BIC的变分贝叶斯近似,即使没有明确定义数据集维度和个数,仍然可以用VBIC进行模型的选择。但是,上述文献中,直接为先验分布的参数设置一个超先验分布,并没有说明设置超先验分布时模型的参数估计效果。为了解决这个问题,本文为数据样本建立FA模型,并提出一种新的变分贝叶斯推断算法,用于FA模型的参数估计,重点讨论因子分析模型中超先验分布对变分贝叶斯估计结果的影响。
1 因子分析模型
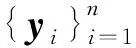
yi=Axi+ξi,i=1,…,n
(1)
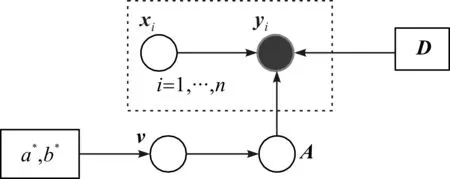
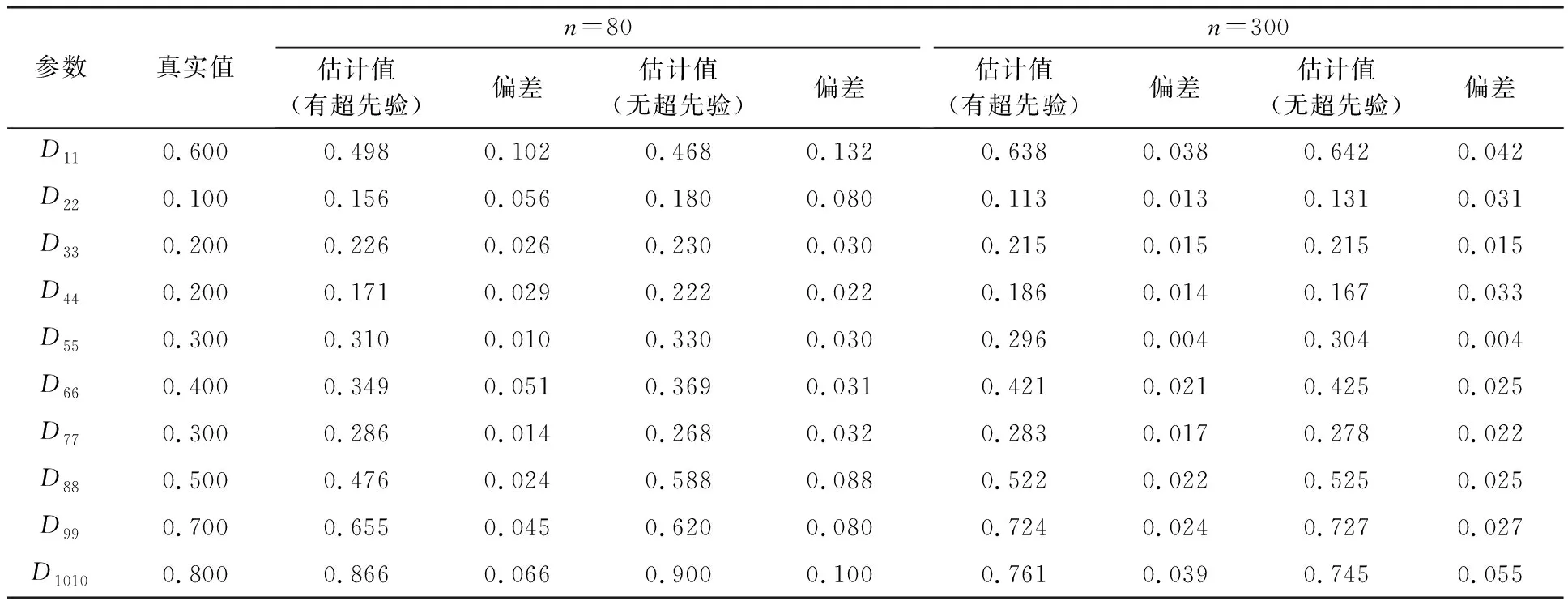
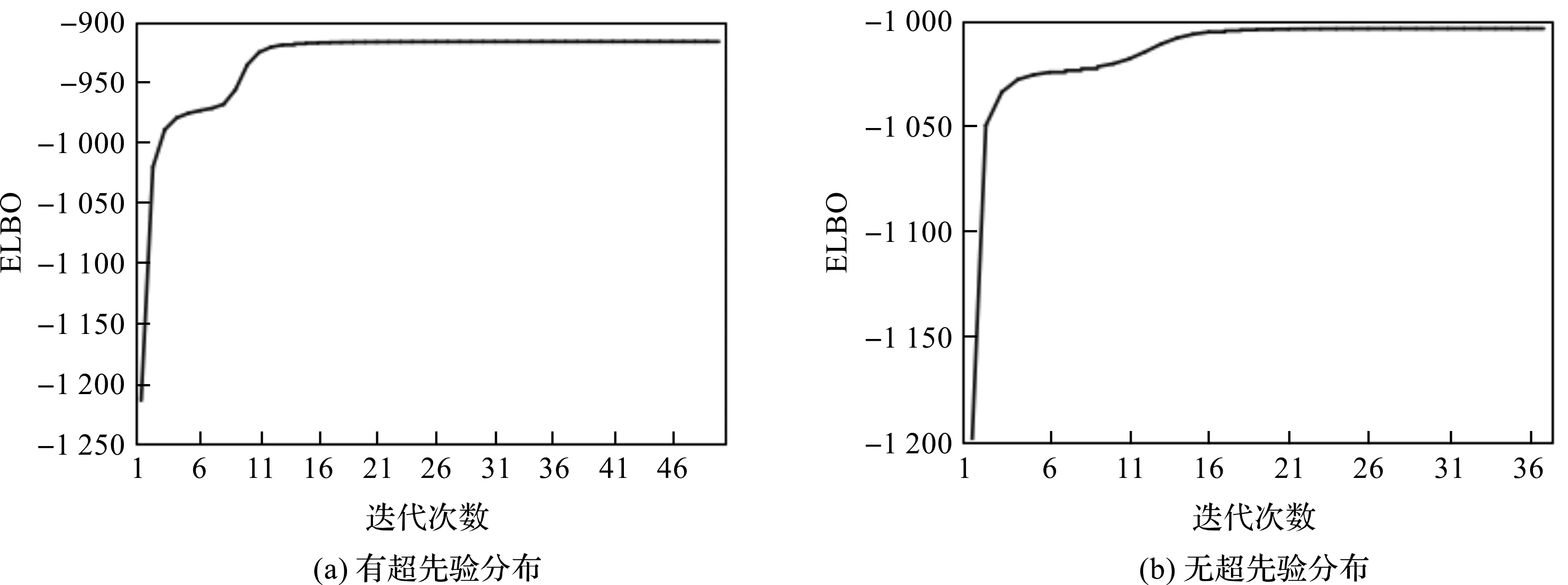
式中,xi为k(k 假设观测值yi∈Rp是连续的,就像线性回归一样,设均值是(隐变量)输入的线性函数,从而似然函数为: p(yi|A,D,xi)=N(yi|Axi,D) (2) 在贝叶斯框架中,模型的参数被视为随机变量,因此需要设置参数的先验分布。在共轭指数域内,为了保证先验分布和后验分布具有一致性,在变分贝叶斯推断算法中将参数的先验分布设置为共轭先验分布,否则,很难求出变分后验分布的具体形式。详细的选择过程如下。 参考文献[1]中对于因子载荷矩阵A的先验分布设置,假设A的每一列服从相同均值和不同精度的高斯分布, (3) 式中,A.j表示矩阵A的第j列;v={v1,…,vk}是一个随机变量,考虑到对A分布的影响,选择在精度v的每一个元素上放置一个超先验分布: (4) 式中,a*和b*分别为形状参数和逆尺度参数。A的分布从行向量的角度进行描述: (5) 式中,Aq.表示矩阵A的第q行;diag(v)为对角线上元素为{v1,…,vk}的对角矩阵。 因为D的自由度数不随组件的维数增加而增加,所以,进行参数的先验分布假设时,没有假设D的先验分布,而是把D当成超参数直接进行优化。用概率图形来表示FA的模型结构,如图1所示。 图1 FA概率图形模型 (6) 对于采样后的数据集,根据贝叶斯定理,参数和隐变量的后验分布表示为: (7) 事实上,可以采用最大似然估计或最大后验估计等点估计的方式来求解式(7)的后验分布,但在此模型中,联合概率分布函数比较复杂,采用上述方法很难求解,因此本文提出一种变分贝叶斯推断算法,用一种简单的分布q(θ)来近似后验分布,假定Z是不可观测变量的概率密度分布族,q(θ)∈Z。为了描述q(θ)与p(θ|y)的逼近程度,引入相对熵(Kullback-Leibler,KL),即: (8) 依据泛函理论[8],证据下界L(q)关于q(θ)的泛函求导,得到各参数的通解表达式: lnq(θj)=Ei≠jlnp(y,θ)+c (9) 式中,Ei≠j[lnp(y,θ)]为联合概率密度函数的期望不涉及第j个变分因素,c表示不依赖于参数θj的常数。 假设因子载荷矩阵A的共轭先验分布中的参数v有超先验分布,此时对应的模型称为有超先验分布的FA模型。根据式(9)计算出有超先验分布的FA模型中各组参数的变分后验分布。 2.1.1 因子载荷矩阵A的第j列的精度vj的变分后验分布 由图1可以看出,精度vj的更新可以利用因子载荷矩阵和参数的先验信息推导得出,由共轭性知,vj,∀j∈[1,k]的变分后验是Gamma分布,即 lnGa(vj|a,bj) 具有形状参数a和逆尺度参数bj,后验参数可利用下式更新: (10) 其中Aqj表示因子载荷矩阵的第q行第j列,〈·〉表示对相关后验分布的期望。 2.1.2 q(A)的变分后验分布 A的更新可以利用参数的先验信息和可观测数据的联合估计信息推导得出, 其中tr(·)为迹函数,q(A)可以写成行向量的后验分布的乘积,即: 参数的更新公式为: (11) 2.1.3 隐变量xi的变分后验分布 隐变量xi的后验推断利用(2)式似然函数的信息和xi的先验信息进行推导, lnq(xi)=EAlnp(yi|A,xi,D)+lnp(xi)+c= (12) 根据式(10)—式(12),计算得到参数更新公式中的期望值为: 2.1.4 模型的证据下界 根据参数的先验分布和变分后验分布信息,计算式(8)的证据下界L(q), (13) 另外,相对于参数D,通过L(q)对D的求导来更新D,此对角矩阵的第q个元素Dqq为: (14) 将式(10)—式(12)、式(14)的更新关系代入式(13),不断迭代更新模型的参数直到证据下界收敛,当L(qt)-L(qt-1)<ε时,说明L(q)达到收敛状态,迭代停止,否则,再进行下一次迭代。其中L(qt)表示第t次迭代证据下界的值,ε表示阈值。L(q)的具体表达式在此不再展开。 综上所述,整个算法流程如下。 输入:数据集y1︰n以及因子的个数k输出:变分密度q(θ),变分下界L(q)初始化:隐变量xi的均值和方差,以及D,超参数a*,b*(1)通过式(10)—式(12)、式(14)更新超参数;(2)通过计算得到证据下界L(q);(3)当L(qt)-L(qt-1)<ε,L(q)达到收敛状态,迭代停止,否则,重复步骤1至步骤3;(4)输出变分密度q(θ),变分下界L(q)。 参数的更新公式为: (15) 变分下界变为: (16) 参数D只与似然函数有关,因此D的更新形式没有发生改变,如式(14)。 为了比较有超先验分布的FA模型和无超先验分布的FA模型中,变分贝叶斯推断算法对参数估计的效果,可以采用一种标准进行衡量。在早期的研究中,主要利用赤池信息准则(Akaike Information Criterion,AIC)、贝叶斯信息准则BIC、偏差信息准则(Deviance Information Criterion,DIC)等比较模型的好坏[9]。本文中,主要采用变分贝叶斯信息准则VBIC对模型进行选择,在不知道数据集维度和个数情况下,VBIC仍可以进行模型的选择。VBIC是BIC的变分贝叶斯近似,表达式定义为[6]: VBIC=-2L(q)+2Eq[lnp(θ)] 根据式(13)、式(16)和参数的先验信息,得到有超先验分布的FA模型和无超先验分布的FA模型的VBIC分别为: (17) 本文中,运用VBIC比较有超先验分布的FA模型和无超先验分布的FA模型的优劣,VBIC的值越小,说明模型的参数估计效果越佳。 运用式(1)生成一个高维数据集,且样本容量是可变的,为了方便起见,选择特征个数p=10,公共因子的个数k=2,模型参数的真实值为: D=diag(0.6,0.1,0.2,0.2,0.3,0.4,0.3,0.5,0.7,0.8) 为了避免在更新迭代过程中出现跟踪停滞问题,通常为共轭先验分布中的超参数设置一个初始值[10]。变分贝叶斯推断算法对初始值不敏感,本文设定的初始值与真实值较近,目的是让迭代步骤更少。将模型的参数初始化设置为:a*=10,b*=1,xi的均值设定为[-0.040,0.011],xi的方差设置为I,噪声方差的对角线元素均设置为0.01,当参数无超先验分布时,v设置为[50,100]。采用本文提出的变分贝叶斯推断算法进行FA模型参数的估计,并运用VBIC进行模型的选择。 本文在样本容量n=80和n=300下,分别对有超先验分布的FA模型和无超先验分布的FA模型的参数进行变分贝叶斯估计,由于参数个数较多,估算结果只给出参数D的估计及真实值和估计值之间的偏差绝对值,如表1所示。 表1 参数D的估计值和真实值的偏差 从表1可以看出,即使是在小样本的情形下,运用有超先验分布的变分贝叶斯推断算法和无超先验分布的变分贝叶斯推断算法对不同FA模型的参数进行估计,参数的估计值和真实值的偏差绝对值都很小,例如,超过50%的偏差绝对值小于0.050,大约有90%的偏差绝对值是小于0.100,这证明了变分贝叶斯推断算法在FA模型的参数估计上的有效性。在小样本和参数无超先验分布的情况下,参数估计量的精度不够高,不同模型和样本容量下,参数估计均存在一定误差,这是因为变分贝叶斯算法是近似推断而非精确推断。而当样本容量较大以及参数有超先验分布时,参数的估计值和真实值更逼近,说明本文提出的变分贝叶斯推断算法更适合较大的样本容量和有超先验分布的FA模型,可以通过扩大样本的容量和设置参数的超先验分布来减少参数估计的误差,提高参数估计精度。 变分下界的迭代收敛过程如图2所示,迭代设置的阈值ε=10-3,迭代的最大次数设置为1 000。有超先验分布的变分贝叶斯推断算法和无超先验分布的变分贝叶斯推断算法的目标函数的变化趋势如图2所示。从图2可以看出,随着迭代次数的增加,变分下界不断增加,直到收敛。 图2 变分下界的迭代收敛过程 在不同数据集下,对有超先验分布的FA模型和无超先验分布的FA模型的迭代次数、ELBO,VBIC进行比较,结果如表2所示。 表2 不同数据集下,不同FA模型的衡量指标比较 ELBO是边际似然的下界,当ELBO的值越高,说明模型对数据拟合程度越好,模型产生数据的概率也越高。由表2可以看出,在不同样本容量下,有超先验分布的FA模型的ELBO值更大一些,并且有超先验分布的FA模型的VBIC小于无超先验分布的FA模型。综合来说,有超先验分布的FA模型对数据的拟合程度更好,因此,有超先验分布的FA模型是最好的选择。 本文提出一种有关FA模型的变分贝叶斯推断算法,重点讨论FA模型中超先验分布对变分贝叶斯估计结果的影响,并采用变分贝叶斯信息准则进行模型的选择。实验研究发现,当参数设置超先验分布时,FA模型的参数估计效果更佳。后续计划将本文算法应用于结构方程模型(Structural Equation Modeling,SEM)的参数估计和模型选择中。
2 变分贝叶斯推断
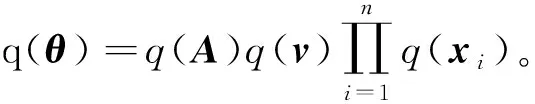
2.1 有超先验分布的变分贝叶斯推断

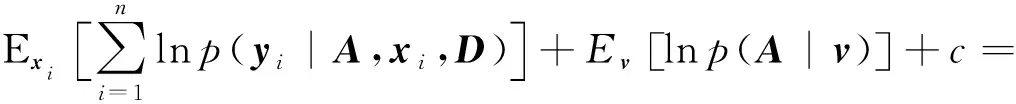

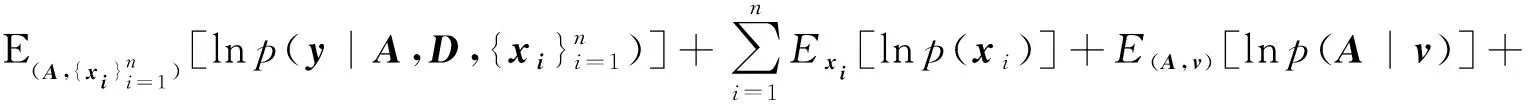


2.2 无超先验分布的变分贝叶斯推断
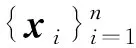
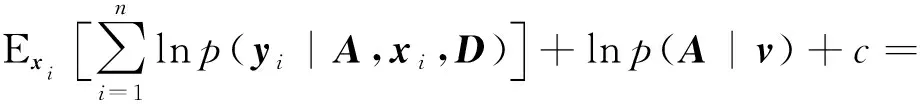
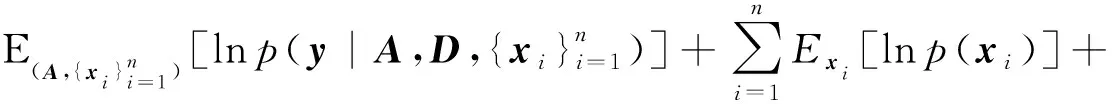
3 变分贝叶斯信息准则
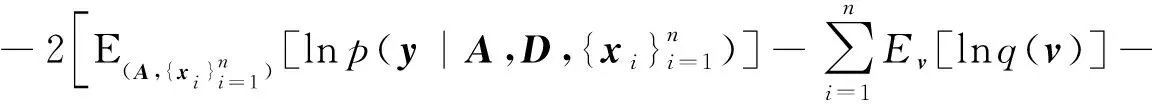
4 实验结果与分析


5 结束语
