基于不完备信息系统的三支冲突分析
2022-06-07杨文听易黄建李小南
杨文听,易黄建,陈 跃,李小南
(1 西安电子科技大学 数学与统计学院,陕西 西安 710126;2 西北大学 信息科学与技术学院,陕西 西安 710127)
Pawlak提出的粗糙集理论是一种处理不确定性问题的有效工具,此外,概率粗糙集[1-2]和决策粗糙集[3-5]作为经典粗糙集模型的重要推广,也是处理不确定问题的一种有效方法。Yao等在粗糙集和决策粗糙集的基础上提出三支决策理论[6-7],作为粗糙集的一个有效改进模型,三支决策同样是处理不确定性和复杂问题的有效工具且得到广泛应用。Hu等在三支决策空间中提出了2种新型的三支决策,并讨论了参数变化及三支决策的性质等问题[8];Sun等研究了在论域上基于多粒度模糊决策理论粗糙集的三支群决策[9];Li等将包含关系推广至一般评价函数,研究了双论域上的三支决策,提出了一种计算阈值的方法[10];Li等将三支决策模型从0-1表推广到一般的信息表,研究了现有相关模型间的联系,提出加权信息熵这一测度来确定阈值和最优的三划分[11]。
冲突是反映支持与反对的一种对立状态,为更好地解释冲突问题,Pawlak提出了基于粗糙集理论的冲突分析,而冲突分析与三支决策之间存在着某些天然的联系[12-13]。因此,部分学者开始将三支决策的思想用于冲突分析的研究中[14-16]。如Lang等在决策粗糙集和三支决策理论的基础上,通过推广Pawlak冲突分析模型,引入了冲突分析的概率模型,使用一对阈值而不是Pawlak模型中的阈值0.5来定义联盟、冲突和中立关系[17];Sun等提出了一种基于粗糙集逼近算子的冲突分析方法[18];Fan等以基于评价的三支决策模型为基础,并运用形式概念分析中的求导算子研究了冲突分析的定量模型[19];Yao等将Pawlak的冲突分析模型进行推广重构,通过一个距离函数定义代理间的三支冲突模型[20]。
在分析冲突原因和寻求冲突解决办法时,通常需要统计各个代理对问题的态度值,并整理成信息表。理想情况下,我们假设每个代理对问题都给出支持、中立或反对态度,即每个代理的态度值都是可获取的,不存在缺失的情况。这样理想状态下获得的态度值表,称之为完备信息表。目前,大多数学者对冲突分析所做的研究也正是基于完备信息表,如Lang等提出基于毕达哥拉斯模糊集理论的三支群冲突分析[21];Sun等提出基于概率粗糙集的冲突分析[22],Yao等提出基于Pawlak模型拓展的三支冲突分析[20];Li等提出将一般的信息系统推广到三角模糊信息系统中,用相对面积来定义代理对问题的态度,再对问题赋予模糊权重,最后根据决策理论粗糙集计算阈值得到代理的三划分,从而建立了三角模糊信息系统的冲突分析模型[23];Bashir等提出了用博弈论和粗糙集来解决冲突[24]。但是,人类社会的冲突往往是动态复杂的,代理对问题的态度受各种因素的影响,代理可以给出明确的态度,也可以保持沉默,这就很有可能造成部分代理态度值暂时或永久的缺失,从而得到的是不完备信息系统[25]。Liu等提出了在不完备信息系统中一种新的三支决策模型[26];Luo等提出了基于相似性和满意度的不完备信息三支决策[27]。因此,将冲突分析从完备的信息系统推广到不完备的信息系统是十分有意义的。本文将在不完备信息系统背景下,重新建立一个新的三支冲突分析模型进行问题研究。首先,介绍了完备信息系统下的冲突分析,在此基础上将其推广至不完备的信息系统中。其次,通过处理信息表中的缺失值定义了代理之间的冲突相似距离,进一步定义了代理之间的冲突关系,从而建立了不完备信息系统上的三支冲突分析模型。最后,基于决策理论粗糙集,并运用贝叶斯最小风险决策原理得到了该模型中代理三划分所需的阈值,从而得到最为合理的决策结果。
1 相关知识
1.1 完备信息系统下的冲突分析
定义1[12](三值信息系统)三值信息系统是一个四元组S=(U,A,Va,f),其中U={x1,x2,…,xn}是一个非空有限代理集,A={a1,a2,…,am}是一个非空有限问题集,a(∈A)的值集Va={-1,0,+1},f:U×A→Va是一个二元映射。
注1在以上三值信息系统中,用二元映射f表示代理对问题所持的态度,即∀xi∈U,aj∈A,若f(xi,aj)=-1,表示代理xi对问题aj持反对态度;f(xi,aj)=0,表示代理xi对问题aj持中立态度;f(xi,aj)=+1,表示代理xi对问题aj持肯定态度。
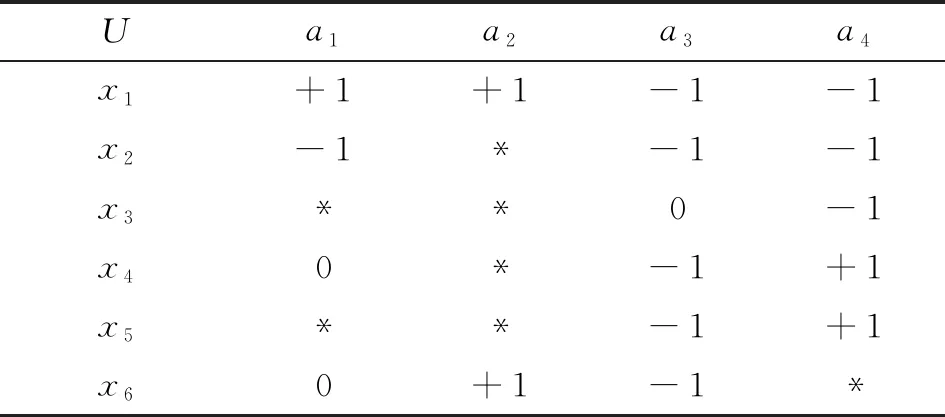
表1是一个三值信息系统,其中每个代理对问题都给出了清晰明确的态度,不存在态度值缺失或暂时不明晰的情况,因此这是一个完备信息系统。下面介绍一个辅助函数来描述一对代理间的关系。
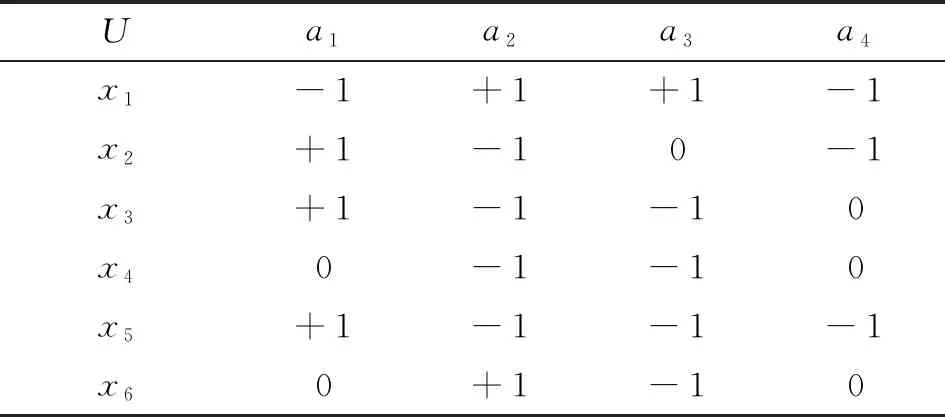
表1 完备三值信息系统
定义2[12]对每个a∈A,代理间的一个二元关系φa:U2→{-1,0,1}定义为
若φa(x,y)=1,则代理x和y对问题a持相同的态度,即代理x和y在问题a上是联盟的;若φa(x,y)=0,则x和y至少有一个对问题a持中立态度,即代理x和y在问题a上是中立的;若φa(x,y)=-1,则x和y对问题a持有相反的意见,即代理x和y在问题a上是冲突的。
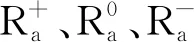


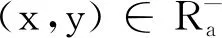
以表1为例,对于问题a1,可得
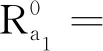
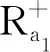
定义3[12]设S=(U,A,Va,f)是一个三值信息系统,问题集∅≠B⊆A,代理x与y的距离函数
其中
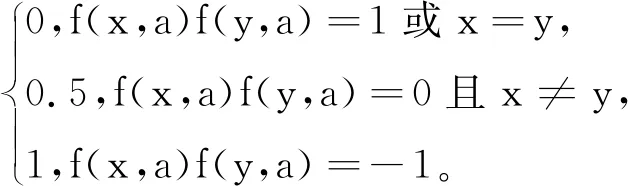
定义4[17]设S=(U,A,Va,f)是一个三值信息系统,问题集∅≠B⊆A,α、β是一对给定阈值且满足0≤β<α≤1,则代理对(x,y)∈U2在问题集B上的关系如下:

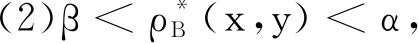

定义5[17]设S=(U,A,Va,f)是一个三值信息系统,问题集∅≠B⊆A,α、β是一对给定阈值且满足0≤β<α≤1,定义代理x的联盟、中立和冲突集如下:
1.2 概率粗糙集近似
定义6[2]设S=(U,A,Va,f)是一个信息系统,α、β是一对给定阈值且满足0≤β<α≤1,则X(⊆U)的上下近似定义为
r(α,β)(X)={x∈U|P(X|[x])≤β}。
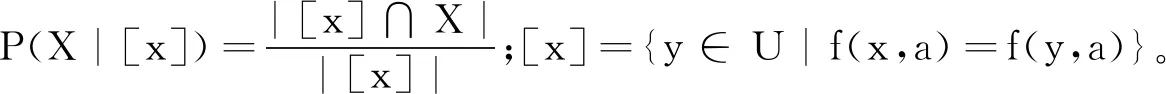
定义7[2]设S=(U,A,Va,f)是一个信息系统,α、β是一对给定阈值且满足0≤β<α≤1,X(⊆U)的概率正、负以及边界域P(α,β)(X)、N(α,β)(X)、B(α,β)(X)为
P(α,β)(X)={x|U|P(X|[x])≥α};
N(α,β)(X)={x∈U|P(X|[x])≤β};
B(α,β)(X)={x∈U|β 注2由上述定义可知,正域、边界域以及负域的三划分与阈值的大小密切相关。因此,可以将其运用在不完备信息系统的冲突分析中,从而可以得到在不完备信息系统中阈值的大小以确定代理的三划分。 定义8[25]不完备信息系统是一个四元组S=(U,A,Va∪{*},f),其中U={x1,x2,…,xn}是一个非空有限代理集,A={a1,a2,…,am}是一个非空有限问题集,a(∈A)的值集Va={-1,0,+1,*},f:U×A→Va是一个二元映射。 注3在不完备信息系统中,-1、0、+1表示的含义与完备信息表相同,*表示信息缺失。 对于缺失值*,它表示代理对于问题的态度,且对决策起着十分重要的作用。缺失值*可能为Va的子集,即Bai⊆Va,|Bai|>0。从而将不完备的信息表转换为完备的信息表,即表2、表3。 表2 不完备信息表 表3 混合信息表 定义9设S=(U,A,Va∪{*},f)是一个不完备信息系统,问题集∅≠B⊆A,则代理x和y的相似距离函数为 S(ai)(x,y)= S(ai)(x,y)=1表示代理x和y对问题ai的态度一致且不缺失的情况下,二者间的相似程度; S(ai)(x,y)=0表示代理x和y对问题ai的态度不一致,且其中一个代理对问题持中立态度,另外一个代理对问题的态度缺失情况下,二者间的相似程度; S(ai)(x,y)=-1表示代理x和y对问题ai的态度不一致,一个代理对问题持支持,另外一个代理对问题持反对态度的情况下,二者间的相似程度; 定义10设S=(U,A,Va∪{*},f)是一个不完备信息系统,问题集∅≠B⊆A,则代理x和y的冲突相似距离为 式中:|B|表示问题集B的基数;SB(x,y)表示代理x和y面对多个问题时,二者间的平均相似程度。 注4该定义的冲突相似距离表示的是两个代理之间相似程度的大小。若两个代理的冲突相似距离越大,则联盟机率越大;反之,若冲突相似距离越小,则具有冲突的机率越大。 由以上的冲突相似距离,可得以下性质。 性质1(1)0≤S(x,y)≤1; (2)S(x,y)=S(y,x); (3)S(x,y)=1,当且仅当x=y。 例1在不完备信息系统中(如表2),对缺失值进行处理可重新得到一个完整的混合信息系统,如表3。代理间对单个问题的态度相似程度可以通过定义9的冲突相似距离计算得到: Sa3(x1,x2)=1,Sa4(x1,x2)=1。 表4 代理对多个问题的冲突相似距离 采用政治选举问题表示这个不完备信息表,U={x1,x2,x3,x4,x5,x6}代表6个选民,即代理集,A={a1,a2,a3,a4}代表4个党派,即问题集。在不完备信息系统的背景下,研究选民对党派的支持与否,从而得到选民间的联盟、中立以及冲突关系,并且它是根据以上得到的冲突相似距离而确定的。冲突相似距离越大,说明选民对党派所表明的态度一致,因此可以判断为联盟机率较大;冲突相似距离越小,说明选民对党派所表明的态度不一致,因此二者之间的冲突较大;其余则为中立者。 将Pawlak模型这一完备信息系统推广至不完备信息系统上,从而研究不完备状态下的冲突分析情况。在不完备信息系统中,将冲突相似距离这个相似度作为冲突函数,从而得到代理之间的联盟、中立以及冲突关系。 定义11设S=(U,A,Va∪{*},f)是一个不完备信息系统,问题集∅≠B⊆A,∀x,y∈U,则代理x与y之间的冲突函数为 冲突函数的大小在一定程度上表示了代理x与y的冲突程度。 定义12设S=(U,A,Va∪{*},f)是一个不完备信息系统,∀x,y∈U,α、β是一对给定阈值且满足0≤β<α≤1,x与y的冲突函数为S(x,y),则x与y在问题集B上的关系如下: (1)S(x,y)≥α,表示代理x与y是联盟关系; (2)β (3)S(x,y)≤β,表示代理x与y是冲突关系。 定义13设S=(U,A,Va∪{*},f)是一个不完备信息系统,∀x,y∈U,α、β是一对给定阈值且满足0≤β<α≤1,则可定义代理的冲突、中立以及联盟集: (1)AL(x)={y∈U|S(x,y)≥α}; (2)NE(x)={y∈U|β (3)CO(x)={y∈U|S(x,y)≤β}。 由定义12、13可知,所得到的联盟、中立及冲突集与阈值有关。阈值的大小决定着代理间的关系,但当α=1时,代理间的冲突最小,联盟意愿最强;β=0时,代理间的冲突最大,联盟意愿几乎没有。 定理1设S=(U,A,Va∪{*},f)是一个不完备信息系统,根据定义13可知, (1)y∈AL(x)⟺x∈AL(y); (2)y∈NE(x)⟺x∈NE(y); (3)y∈CO(x)⟺x∈CO(y)。 证明:(1)由y∈AL(x),得S(x,y)≥α,又由性质1得S(x,y)=S(y,x),所以得到S(y,x)≥α,即得到AL(y)={x∈U|S(y,x)≥α},所以x∈AL(y)。 (2)由y∈NE(x),得β (3)由y∈CO(x),得S(x,y)≤β,又由性质1得S(x,y)=S(y,x),所以得到S(x,y)≤β,即得到CO(y)={x∈U|S(y,x)≤β},所以x∈CO(y)。 例2根据表4的冲突相似距离结果,得到以下结果。 在表4中,由于知道每个代理对多个问题的冲突相似距离,根据定义13可得每个代理对多个问题的联盟集、冲突集以及中立集。 若取定阈值α=0.55,β=0.4,每个代理对应的联盟集、冲突集以及中立集如表5。 表5 每个代理在多个问题中的联盟集、冲突集以及中立集 以上例子表明,通过冲突相似距离以及给定的阈值得到了关于每个选民的联盟集、中立集以及冲突集,但由于给定的阈值具有随机性,导致在一定的程度上可能存在着决策的风险。因此,下面通过决策理论粗糙集来确定阈值的大小,从而得到风险较小的决策结果。 决策理论粗糙集是在2个状态和3个行动中运用的,特征状态集Ω={X,┐X),这里X表示属于X的代理对问题持支持态度,而┐X表示不属于┐X的代理对问题持反对或者否定的态度。D={aP,aB,aN}表示行动集,这里P、B、N表示在决策中的3种行动方式,分别决定x∈AL(X),x∈NE(X),x∈CO(X)。关于3种行为在2种状态下的风险或成本的损失函数由一个3×2矩阵(表6)给出。 表6 不同状态下的损失函数矩阵 在这个矩阵中,λPP、λBP、λNP表示代理在支持状态下,在3种行动aP、aB、aN下遭受的损失。同样,λPN、λBN、λNN表示代理在反对或者中立状态下,在3种行动aP、aB、aN下遭受的损失。由于本文研究的是不完备信息系统的三值表,因此在本文中所涉及的损失函数考虑采用单值函数。 由定义9可得在不完备信息系统上的相似性关系。 a∈B}。 这里h表示一个阈值,只有在冲突相似距离大于h时,才会确定代理间的相似关系,从而得到两代理之间较高的相似程度。 定义15设S=(U,A,Va∪{*},f)是一个不完备信息系统,对∅≠B⊆A,则∀x∈B,相似类可定义为 在不完备信息系统中,根据相似关系得到代理的相似类,对某一类问题可以得到代理间意见相对一致的集合,这在根据粗糙集决策理论进行三支冲突分析中更具有理论价值。 定义16设S=(U,A,Va∪{*},f)是一个不完备信息系统,∀X⊆U,可基于相似关系得到条件概率 定义17设S=(U,A,Va∪{*},f)是一个不完备信息系统,∀X⊆U,∅≠B⊆A,且0≤β<α≤1。X⊆U的上下近似可定义为 定义18设S=(U,A,Va∪{*},f)是一个不完备信息系统,α、β是一对给定阈值且满足0≤β<α≤1,则X⊆U的概率正域、负域、中立,即联盟、冲突以及中立为 由定义17可知,若给定的代理集X在代理xi相似类的条件概率大于等于α时,可知代理U的某些代理是联盟的;若给定的代理集X在代理xi相似类的条件概率在α、β之间时,可知代理U的某些代理是中立的;若假设给定的代理集X在代理xi相似类的条件概率小于等于β时,可知代理U的某些代理是冲突的。 在不完备信息系统中,假设λPP、λBP、λNP、λPN、λBN和λNN是损失函数,满足λPP≤λBP≤λNP,λNN≤λBN≤λPN,则∀x∈U,得到在3种行动aP、aB、aN下的期望损失如下: 根据贝叶斯最小风险决策理论可得定理2。 定理2设S=(U,A,Va∪{*},f)是一个不完备信息系统, ∀x∈U,在3种行动aP、aB、aN下的期望损失为R(aP|x)、R(aB|x)和R(aN|x),则 证明根据贝叶斯最小风险决策原理有 (P)R(aP|x)≤R(aB|x)⟺ λPN-λBN≤[(λBP-λBN)+ R(aP|x)≤R(aN|x)⟺ 同理,得到 (B)R(aB|x)≤R(aP|x)⟺ R(aB|x)≤R(aN|x)⟺ (N)R(aN|x)≤R(aP|x)⟺ R(aN|x)≤R(aB|x)⟺ 令 得到β≤γ≤α。即得到 所以,定理成立。 例3根据例1中的政治选举问题来分析代理之间的冲突关系,表7为政治选举的决策损失矩阵,即λPP、λBP、λNP、λPN、λBN和λNN是损失函数,且满足λPP≤λBP≤λNP,λNN≤λBN≤λPN。 表7 政治选举决策损失函数 若取定h=0.3,可得每个代理的相似类,即在阈值确定的情况下得到每个代理的相似类集合 给定X={x1,x4,x5},且X⊆U,由定义14得 根据定理2,由政治选举决策损失函数可得阈值 再由定义18与定理2决策规则可得联盟集、中立集以及冲突集 对于政治选举,由于选民对问题所持态度不同,选民间会引起不必要的矛盾冲突。通过以上模型得到,当α=0.545、β=0.467时,选民间有一个较为合理的划分:联盟集为{x4,x5},这表明选民x4、x5面对整个事件持有积极的态度;中立集{x6},这表明选民x6对整个事件持有中立的态度;冲突集{x1,x2,x3},这表明选民x1、x2、x3面对整个事件持有消极的态度。因此,在此事件中,以得到的选民三划分为基础,应充分考虑积极者面对整个事件所持有的信息数据,以预测选民间冲突演化的结果,从而为决策者提供有效的信息,这有效地避免了在信息缺少情况下出现的问题,也大大减小了所出现的决策风险,具有一定的应用价值。 本文基于Pawlak的冲突分析模型,将Pawlak模型中完备的三值情况推广至不完备的信息系统中,提出了不完备信息系统中的冲突分析模型。在不完备信息表中,通过对缺失值的处理,将不完备的信息系统转换为完备的信息系统,进而研究代理间的联盟冲突关系。本文定义了一个冲突相似距离,根据这个函数来判定代理间的冲突情况。阈值是冲突分析中一个重要的研究对象,本文根据决策理论粗糙集和贝叶斯最小风险决策原理,确定了阈值的大小,进而得到了最为合理的联盟集、中立集和冲突集。本文是在不完备三值信息表中进行的研究,下一步的工作将推广至模糊集中来讨论研究。2 不完备信息系统下的冲突分析
2.1 不完备信息系统下的冲突相似距离

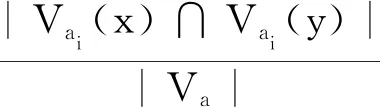
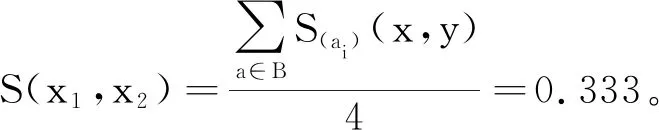
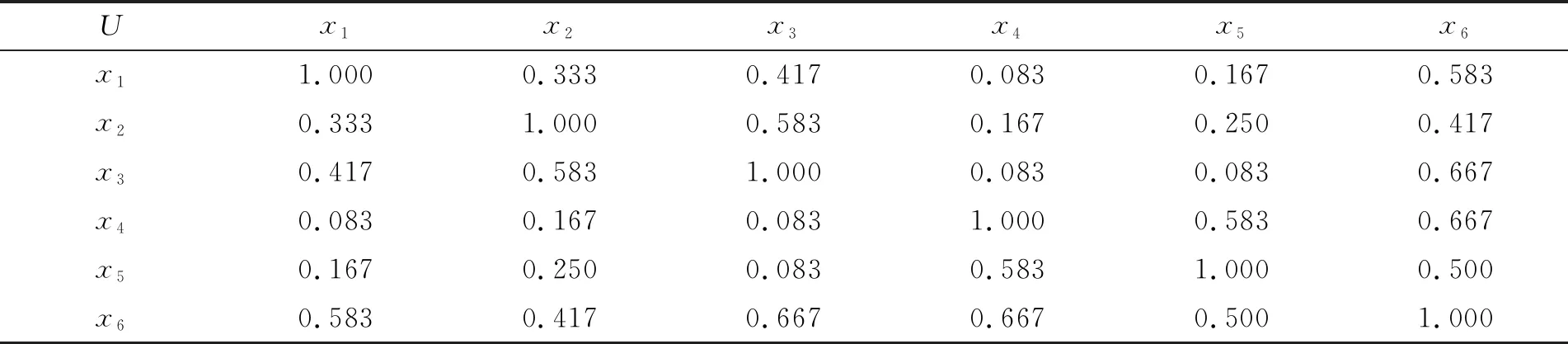
2.2 不完备信息系统下的三支冲突分析

3 基于决策粗糙集理论的冲突分析
3.1 代理的三划分
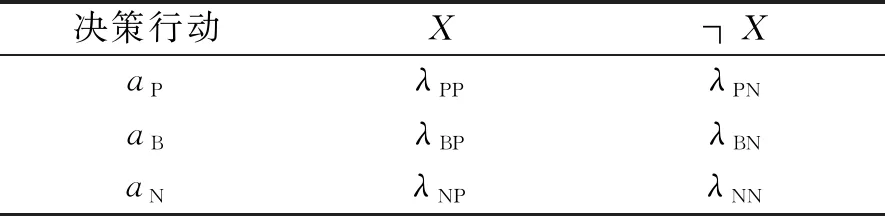

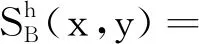

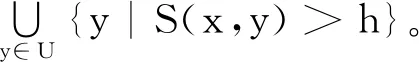




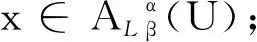


3.2 实例分析

4 结语
