核心素养视角下的阿波罗尼斯圆

赵金丽

核心素养视角下的阿波罗尼斯圆

赵金丽

（杭州市余杭中学，浙江杭州311121）

数学素养是通过数学学习获得的提出、分析与解决问题的能力，本文笔者以阿波罗尼斯圆为授课载体，以培养和提高学生的六大数学核心素养。阿波罗尼斯圆是阿波罗尼斯本人在圆锥曲线内容中留下的美妙一笔。在人教版必修二对于直线和圆的学习章节中，有涉及以阿波罗尼斯圆为背景的习题，可见该内容在学生需要掌握范围内。

数学核心素养；阿波罗尼斯圆；比值；轨迹

本文笔者着重解释了阿波罗尼斯圆的定义、某些重要性质，并给出用阿波罗尼斯圆解决数学问题的范例，并自编两题供练习，以此加强学生的数学建模、直观想象、数学计算以及数学分析等数学核心素养。

一、数学核心素养的概念

数学核心素养包括如下六个方面：1.数学抽象；2.逻辑推理；3.数学建模；4.数学运算；5.直观想象；6.数据分析。史宁中教授指出：数学教学的终极目标，是要让学习者学会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。而数学的眼光就是抽象，数学的思维就是推理，数学的语言就是模型。因此数学教师如何在课堂上渗透数学核心素养成为课堂上的重要责任，而思考问题、研究问题的方法本身高于数学知识的学习，让学生通过数学学习获得的提出、分析与解决问题的能力正是教师们数学教学的重点。

二、阿波罗尼斯圆的背景和定义

在人教版数学选修2-1第二章的《圆锥曲线与方程》章节开头展示了椭圆、双曲线、抛物线可以用对顶的两个圆锥，通过不同的截面得到。

圆

椭圆

抛物线

双曲线

这个方法的创始人是阿波罗尼斯，他的创作可称得上举世无双，为《圆锥曲线》的系统完整奠定了坚实的基础。他对于圆锥曲线的贡献还包括初等数学经常研究的一个特殊圆，后人为了纪念他命名为阿波罗尼斯圆。

这些题的背景都是阿波罗尼斯圆，这类题型内容形式常规，起点低，能保证大部分学生有思路，能够下手。但是数学素养好的学生又会站在阿波罗尼斯圆高层次观点思考问题，可以更快地解决问题，这又有区分度，能够检测出学生的能力，又方便结合数学史上的名题加以设计，因此在命题中常见。

三、阿波罗尼斯圆的方程推导以及性质

（一）方程推导——数学建模

化简整理得：（1－2）2+（1－2）2+2（1+2）+（1－2）2=0 （*）

（1）当=1时，=0，（，）的轨迹是的中垂线；

化成圆的标准形式为：

（二）重要性质——数学运算和数据分析

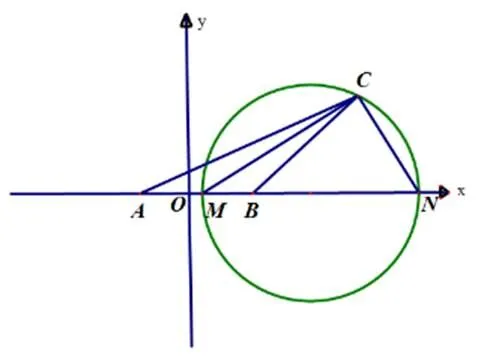
四、例题呈现

解：（阿波罗尼斯圆）

方法一：代数法，利用绝对值不等式

方法二：阿波罗尼斯圆

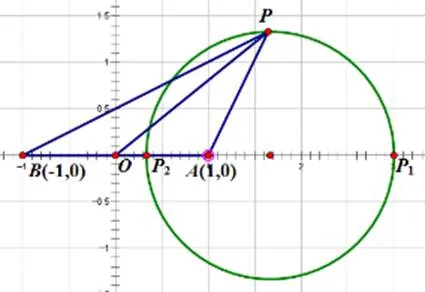
注：当给出的两个定点坐标不是关于原点对称时，可以根据直译法把动点的轨迹方程求出来，而不是直接代公式。

最后，获得了504 896 个学习实例。从GenQA 提供的数据和对齐的数据中分别采样100个样例进行评估，比较两个方法对齐问答对于事实的质量。发现相较于GenQA 中有76% 的匹配事实三元组能够帮助生成自然答案(即是合适的事实)，本文所构造的数据有81% 的匹配三元组是合适的。但是，严格来说只有36% 和44% 的对齐三元组才是正确的能回答问题的三元组。例如，对于问题“谢蓉儿和赵一欢之间的关系是什么?”，匹配的三元组(赵艺奕，职业，艺人)可能有助于生成标准的自然答案“公司艺人”，但它不是回答该问题的正确事实。

注：在讲解例题时利用几何画板辅助教学，培养学生的直观想象和数据分析能力。

A.有且只有一个

B.形成一个圆

D.形成一条直线或一个圆

①当点，不同高的时候，≠1，则点的轨迹是平面α内以为直径的圆，其中,是线段'的内分点和外分点。

②当点,不同高的时候，=1，即=，点的轨迹是平面α内线段'的中垂线，因此本题选D。

注：上面的例3和例4都是用阿波罗尼斯圆的重要性质解决的，当找到比值是定值这个本质之后，就能够抽丝剥茧，回归本质，从而解决题目，培养学生发现问题、归纳概括的能力。

五、自主编题

注：在学习阿波罗尼斯圆后，可适当让学生自主编题，培养学生的数学核心素养，本文提供两个笔者自编题如下：

解：建立如图所示空间直角坐标系，则

六、总结

通过以上三个例题和两个改编题，本文力求探讨数学核心素养的实质，进而在数学教学过程中不断提高教学质量和效率，增强学生的数学素养和能力。

另外可以看到，三角形中有一边是定值，另外两边成比例，只要合理建系，多半可以利用阿波罗尼斯圆解决。这为求解类似问题的最值或者取值范围提供了一条新的路径。用常规方法去解决也有可能有非常漂亮的解法，但是条条大路通罗马，道路多了，可以欣赏各条不同道路的沿途美景。众所周知每条道路上的风景后，当某一天站在高考的战场上，利用我们的慧眼，胸有成竹，信心百倍，可以立马选择一条最快捷的、最成功的“路”。

[1] 朱成万,王红权.至精至简的数学思想方法[M].杭州:浙江大学出版社,2018(4):107-110.

O123.5

A

1002-7661(2022)11-0130-03