基于交通荷载和路面结构特性的动稳定度研究

孙红明，胡小弟，林丽蓉，潘 攀，万九鸣

(1.武汉工程大学 土木工程与建筑学院，湖北 武汉 430074；2.湖北省建筑科学研究设计院股份有限公司，湖北 武汉 430064)

0 引言

动稳定度作为我国工程实践中主要考虑的沥青混合料高温评价指标，单纯地从材料试验的角度来评价沥青混合料高温条件下的抗车辙能力[1-4]。然而，路面的车辙发展不仅仅与路面温度相关，还与作用于路面上的交通量、车辆荷载特性，以及路面结构和结构组成相关[5]。因此，一个合理的沥青混合料动稳定度，应该是基于路面结构和交通荷载的技术指标，而不仅仅只是考虑混合料类型和气候分区。

为了能从荷载设置和结构特性的层面来确定动稳定度指标，首先需要将其应用于路面结构分析之中。考虑到沥青混合料是一种典型的黏弹性材料[6]，本研究的目的在于分析和掌握动稳定度指标同沥青混合料黏弹性参数之间的数量关系，进而将动稳定度转化为可用于有限元分析的材料参数，最终基于此参数进行有限元分析并确定动稳定度、荷载情况、结构属性同车辙深度之间的函数关系，达到从交通荷载和结构特性确定动稳定度指标的目的。

1 原理与方法

早期研究者采用线弹性本构来进行路面结构计算，在如今看来存在许多的不足，而当前已有不少研究者采取黏弹性本构模型来进行沥青路面结构分析[7-8]。经比较，在主流的黏弹性本构模型中Burgers模型具有使用简单、拟合精度高等优点[9]，因此本研究选取Burgers模型进行结构分析。

动稳定度一般由车辙试验得到，本文通过研究车辙试验来确定动稳定度同车辙试验下Burgers模型黏弹性参数之间的关系。整个过程分为2个部分：①基于车辙试验的黏弹性参数的获取与在有限元分析中的应用；②确定动稳定度同车辙试验黏弹性参数的数量关系。

1.1 Burgers模型本构关系

Burgers模型由1个Maxwell单元和1个Kelvin单元串联而成，如图1所示。在一维应力条件下其本构模型为[7]：

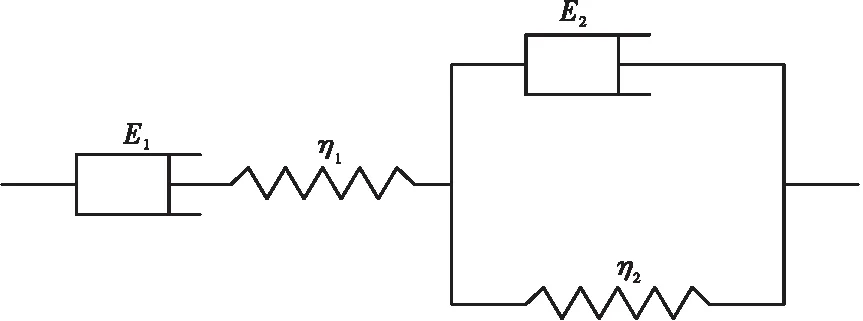
图1 Burgers 模型示意图Figure 1 Burgers model schematic diagram

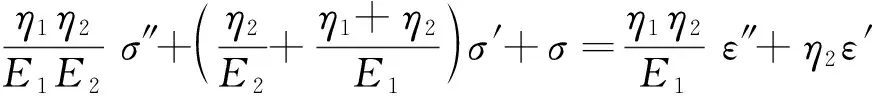
(1)

将阶跃应力函数σ=σ0H(t)代入式(1)后，进行拉普拉斯变化及逆变换，最终得到其蠕变方程：

(2)

1.2 室内车辙试验蠕变方程

参考动态蠕变试验拟合黏弹性参数的方式[10]，本文采取以静代动的方式来处理车辙数据。根据玻尔兹曼叠加原理[11]，试验轮对试件某点的循环碾压可以看作是等效累计时间的静载作用。对标准车辙试验仪，试验轮宽度W=50.0 mm；接触试件长度S=17 mm；1次行走长度L=230 mm；荷载频率H=42次/min；总作用次数N=2 520次。荷载次数与等效作用时间的转化过程如下：

试验轮的速度：V=LH=0.230×42/60=0.161 m/s

试验轮对一点的荷载作用时间(1次轮碾)：t1=S/V=0.017/0.161=0.10 559 s

标准车辙试验60 min内一点的等效荷载作用时间t=N×t1=0.105 59×2 520=266.087 s

不同于单轴动态蠕变、动态模量试验，车辙板在经受车轮反复碾压过程属于有围压的局部加载，此时车辙试验仪所采集的t-ε数据是三维复杂应力状态下的综合应变，因此不能直接用式(2)进行蠕变拟合。已有研究表明[12]，在三维应力状态下，需要采用广义胡克定律，此时沥青混合料(各向同性)的物理方程表示为：

(3)

(4)

(5)

以z为轴向，对于侧向约束而顶面加载的微元，此时侧面由于无法自由变形会产生结构应力σx和σy，二者反过来会影响z向的竖向应变。在微元平衡时，存在：

σx=σy

(6)

以y面为目标面，由于存在约束，式(4)右端为0。将式(6)代入式(4)化简后为：

(7)

解得：

(8)

将式(8)代入式(5)中即可得围压条件下，轴向的物理方程：

(9)

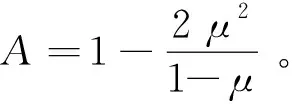
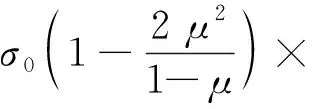
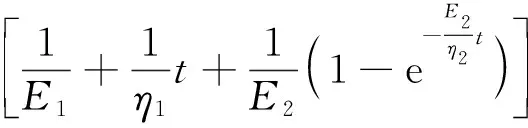
(10)

1.3 动稳定度指标同Burgers模型参数之间的关系

动稳定度与45～60 min内的车辙变形Δd呈反比。由三维应力下的Burgers模型的蠕变方程为式(12)，在固定时间Δt内，永久变形Δd为：

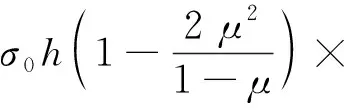
(11)

则动稳定度为：

DS=

(12)

2 试验方案

2.1 混合料的选择

本研究的集料为石灰岩，沥青选用70#基质沥青。采用马歇尔设计方法确定了AC-13和AC-20这2种类型的沥青混合料，最佳油石比分别为4.7%和4.2%。

2.2 室内车辙试验

车辙试验参考《公路工程沥青及沥青混合料试验规程》[13](JTG E20-2011)执行，共选取6种工况进行测试，详情见表1。

表1 1 车辙试验工况Table 1 Rutting test conditions工况混合料类型温度/℃1AC-13452AC-13503AC-13604AC-20455AC-20506AC-2060

2.3 车辙试验的有限元模拟验证

对车辙试验，二维模型截取自垂直与试验轮作用方向的中部截面，模型尺寸300 mm×50 mm。平面单元类型选用Plane183单元，荷载大小为0.7 MPa。选定x为车辙试件宽度方向，y为厚度方向。边界条件为：左右无x方向位移，底面无y方向位移。模型的材料黏弹参数选自Burgers模型的Prony级数，其由Burgers黏弹性参数转化得到。

3 试验数据分析

3.1 基于车辙试验的黏弹性参数拟合

采用式(10)对车辙数据进行非线性拟合，部分工况下结果见图2，R2分别为0.998 9和0.999 3，拟合效果良好。经汇总后，6种工况下的沥青混合料的Burgers模型黏弹性参数见表2，最终可将其转化为Prony级数，此处省略。

3.2 车辙试验有限元验证

考虑6种车辙试验工况，采用ANSYS有限元模拟，动稳定度和60 min车辙深度2个指标计算结果如图3。由图3可知：①对于动稳定度，6种工况下的计算值与实测值之间误差很小。最大误差为工况1时的4.65%；②对于60 min车辙深度，ANSYS计算值与实测数据的差距同样很小。误差最大为工况4时1.66%。以上数据说明基于车辙试验获取的黏弹性参数可用于有限元分析。

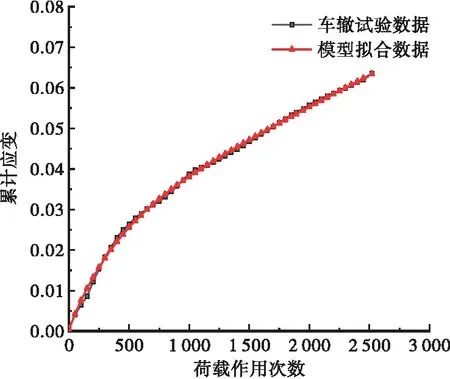
(a) AC-13 60 ℃蠕变拟合曲线

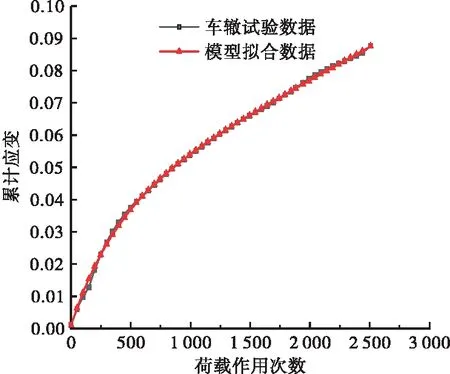
(b) AC-20 60 ℃蠕变拟合曲线

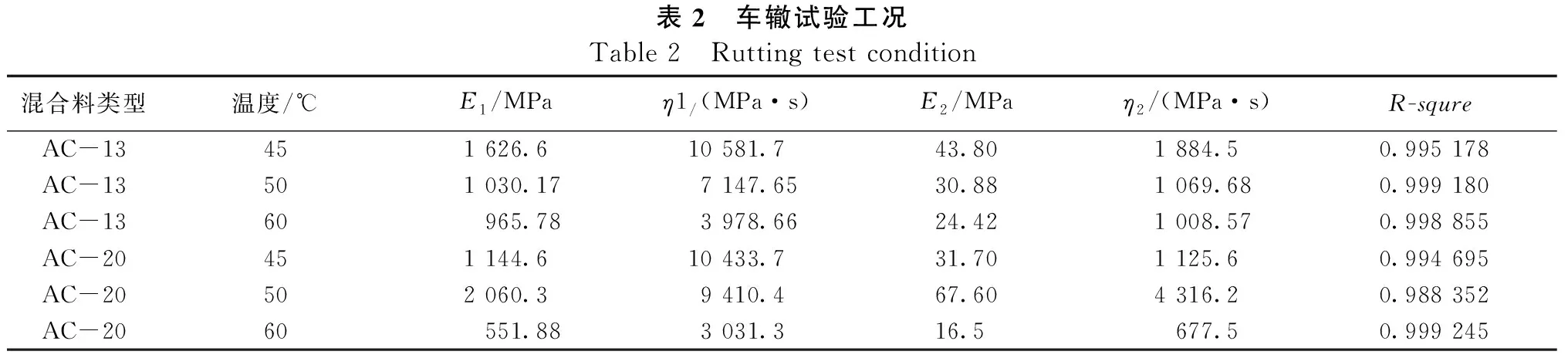
表2 车辙试验工况Table 2 Rutting test condition混合料类型温度/℃E1/MPaη1/(MPa·s)E2/MPaη2/(MPa·s)R-squreAC-13451 626.610 581.743.801 884.50.995 178AC-13501 030.177 147.6530.881 069.680.999 180AC-1360965.783 978.6624.421 008.570.998 855AC-20451 144.610 433.731.701 125.60.994 695AC-20502 060.39 410.467.604 316.20.988 352AC-2060551.883 031.316.5677.50.999 245

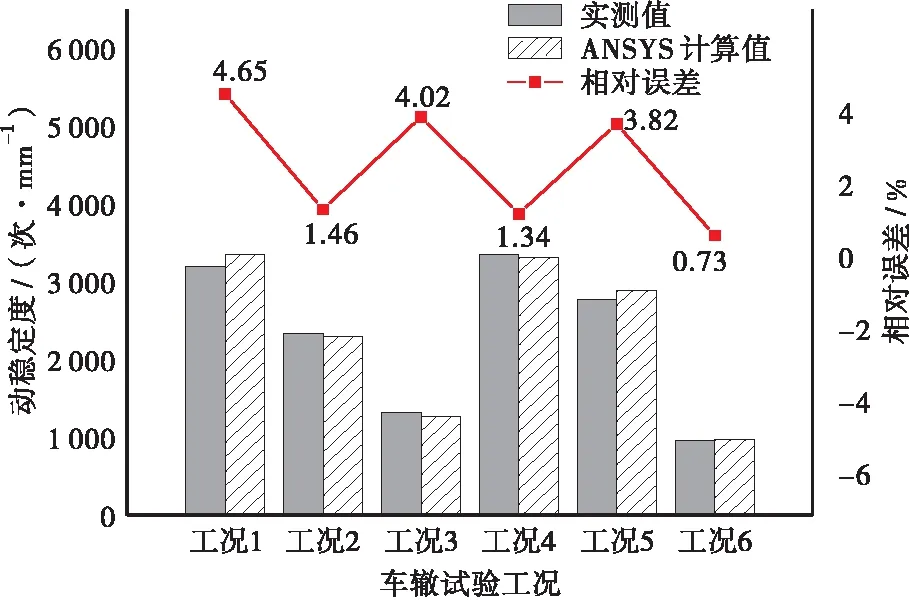
(a) 动稳定度计算结果

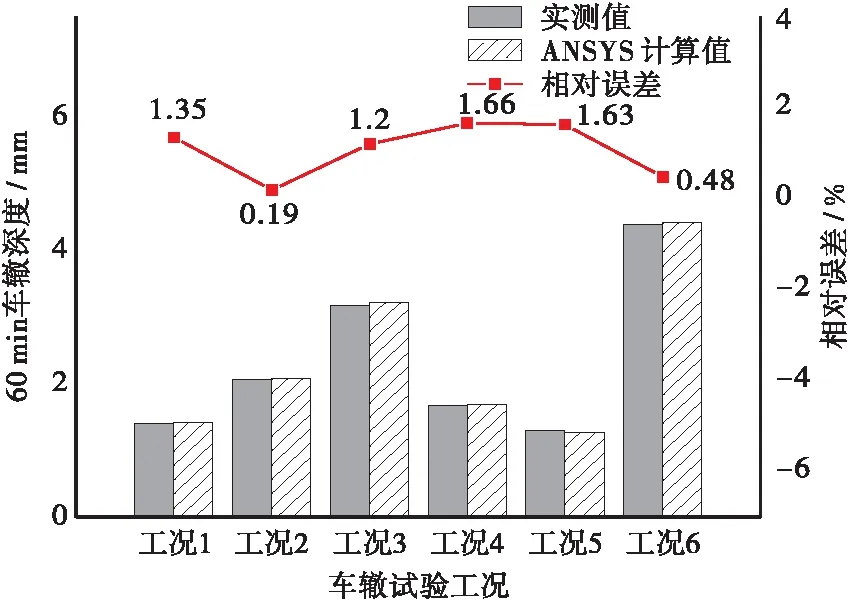
(b) 车辙深度计算结果

3.3 动稳定度同Burgers模型参数之间的关系

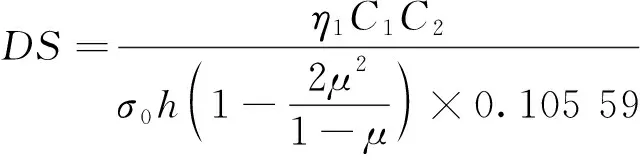
(13)

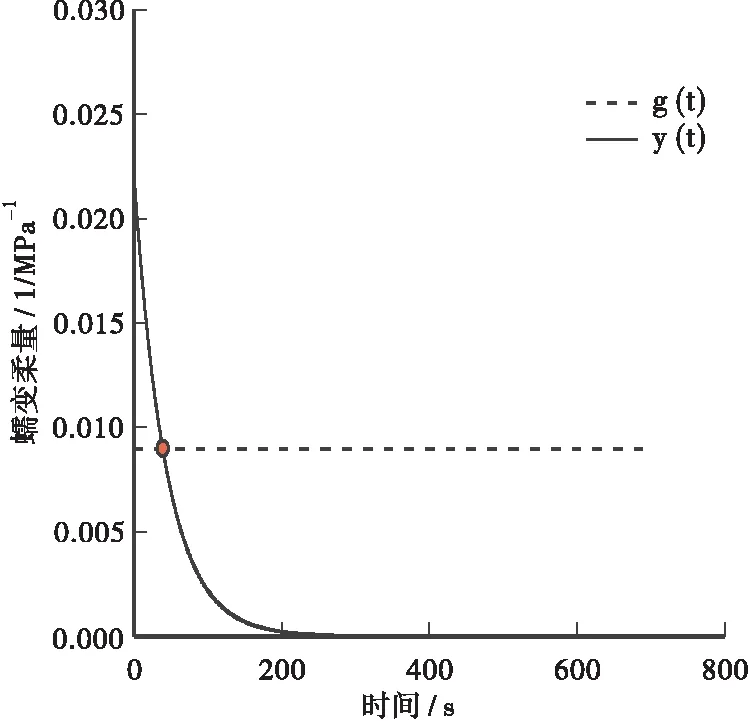
图4 蠕变函数各分项影响曲线Figure 4 Influence curve of each item of creep function

对表2中的黏弹性数据按式(12)进行处理，可得到预估的动稳定度，其与实测结果最小误差为0.39%，最大误差为10.16%。Burgers模型中的其他3个材料参数在数学原理上与DS无直接联系，但是笔者针对大量室内车辙试验的数据从材料层面分析了各参数的分布特性，由于篇幅有限，部分数据见表3。

由表3中的数据分布可以看出，不论在何种温度下：η1/E1取值范围在5～10之间，一般情况可取其平均值6.5；η1/E2的结果一般为140～400之间，数据平均值为258，同时E2一般较小，处于15～40之间，在高温下取较小值；η1/η2数值在4～10之间浮动，平均值为5.8；η2/E2表示延迟时间，决定了车辙曲线的形状变化，其受工况影响较小，取其平均值为45。综上所述，动稳定度综合反映了沥青混合料的抗车辙性能，Burgers模型参数可按照上述方法进行确定。

表3 不同车辙试验工况下Burgers模型参数数量关系Table 3 Quantity relationship of Burgers model parameters under different rutting test conditions混合料类型温度/℃DSE1/MPaη1/(MPa·s)E2/MPaη2/(MPa·s)η1/E1η1/E2η1/η2η2/E21453 1971 626.610 581.743.81 884.56.51 241.59 5.62 43.03 1502 3301 030.177 147.6530.881 069.686.94 231.47 6.68 34.64 1601 317965.783 978.6524.421 008.574.12 162.93 3.94 41.30 2453 3511 144.610 433.731.71 125.69.12 329.14 9.27 35.51 2502 7752 060.39 410.467.64 316.24.57 139.21 2.18 63.85 260959551.883 031.316.5677.55.49 183.72 4.47 41.06 3601 293735.834 106.1220.01921.465.58 205.20 4.46 46.05 4601 7941 030.176 025.7522.741 122.825.85 264.98 5.37 49.38 5601 627772.636 284.3914.66894.318.13 428.68 7.03 61.00 6601 442858.474 631.4918.59886.145.40 249.14 5.23 47.67 7603 6841 144.6311 452.828.241 168.7710.01 405.55 9.80 41.39

4 基于动稳定度的车辙预估模型研究

为了方便计算，本研究以单面层结构进行建模分析，分别考虑动稳定度、温度、荷载压力、轴载次数对路面永久变形的影响。路面结构层次如表4所示。考虑动稳定度和温度对车辙的影响时，黏弹性参数见表5。考虑轴载次数对车辙的影响时，黏弹性参数取DS为1 318次/mm在45 ℃时的参数并假定车速为40 km /h；其他情况下，黏弹性参数取DS为3 000次/mm在60 ℃时的参数。

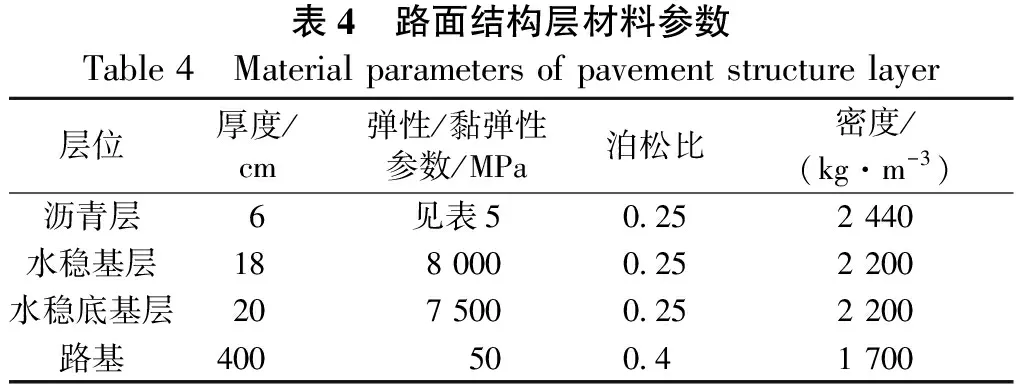
表4 路面结构层材料参数Table 4 Material parameters of pavement structure layer层位厚度/cm弹性/黏弹性参数/MPa泊松比密度/(kg·m-3)沥青层6见表50.252 440水稳基层188 0000.252 200水稳底基层207 5000.252 200路基400500.41 700

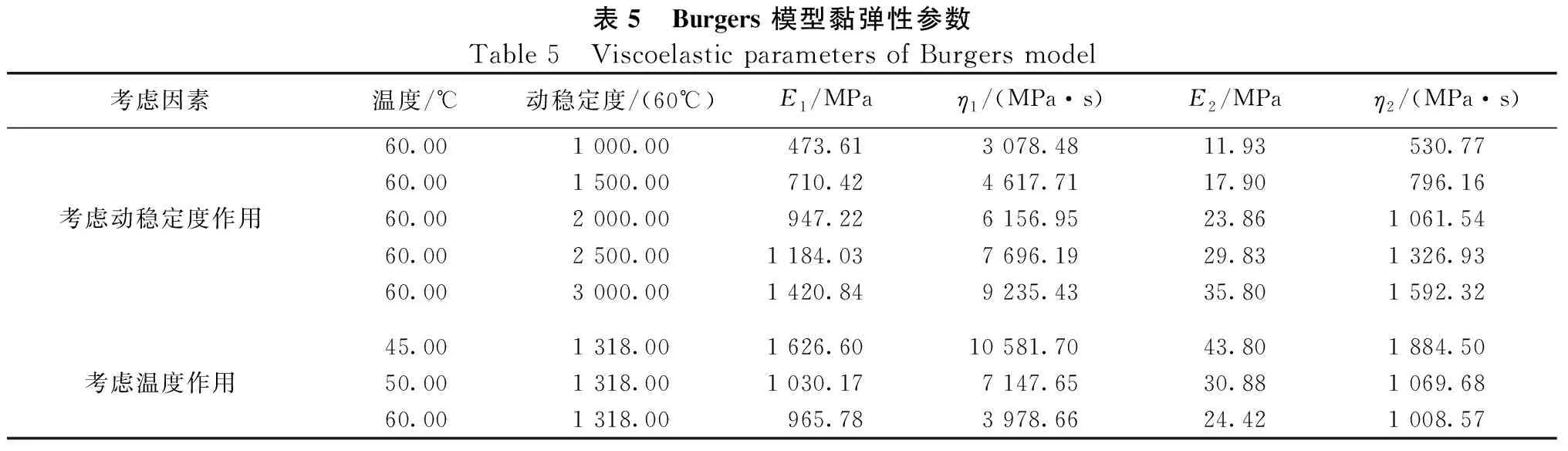
表5 Burgers 模型黏弹性参数Table 5 Viscoelastic parameters of Burgers model考虑因素温度/℃动稳定度/(60℃)E1/MPaη1/(MPa·s)E2/MPaη2/(MPa·s)60.001 000.00473.613 078.4811.93530.7760.001 500.00710.424 617.7117.90796.16考虑动稳定度作用60.002 000.00947.226 156.9523.861 061.5460.002 500.001 184.037 696.1929.831 326.9360.003 000.001 420.849 235.4335.801 592.3245.001 318.001 626.6010 581.7043.801 884.50考虑温度作用50.001 318.001 030.177 147.6530.881 069.6860.001 318.00965.783 978.6624.421 008.57

4.1 动稳定度对车辙深度的影响

仅考虑动稳定度的影响，当环境温度为60 ℃，车速为40 km/h，路面结构承受50万次当量轴载时，计算结果如图5所示。

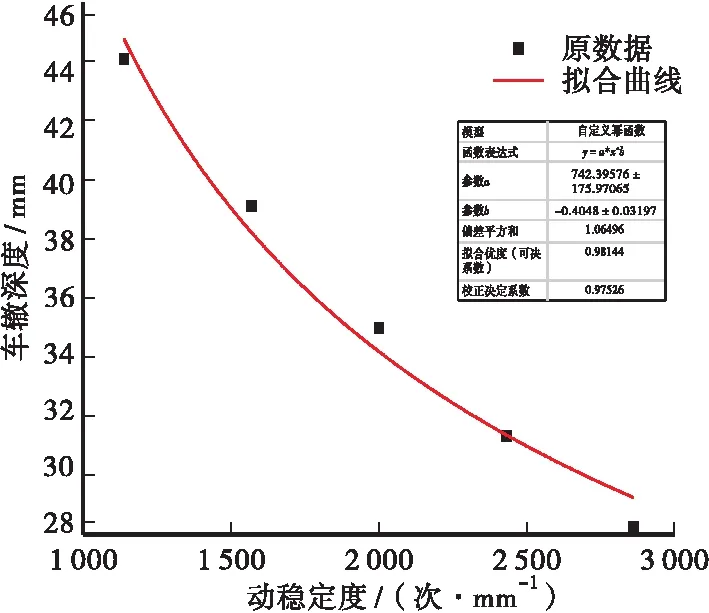
图5 动稳定度对车辙深度的影响Figure 5 Influence of dynamic stability on rut depth

车辙深度随动稳定度的增大而减小，并且曲线斜率也逐步减小，说明在动稳定度在较大水平时，提升动稳定度对抑制车辙发展的收益逐步减小，存在经济性问题，需酌情考虑。本研究采用幂函数进行拟合，R-squre值为0.981 44，说明拟合效果好，此时动稳定度与车辙深度之间的数量关系为：R=742.39×DS-0.404 8。

4.2 温度对车辙深度的影响

同样采用单因子变量原则，仅研究温度对车辙发展的影响。如图6所示，对于同批次沥青混合料，60 ℃的动稳定度相同。在车速为40 km/h，路面结构承受50万次当量轴载时，探寻其在不同温度条件下的车辙发展。此时经计算可知，动稳定度随温度的升高而增大，并且斜率逐步增加。采用幂函数对其进行拟合结果为：R=0.041×T1.696。此时R-squre值为0.985 04，说明拟合效果好。

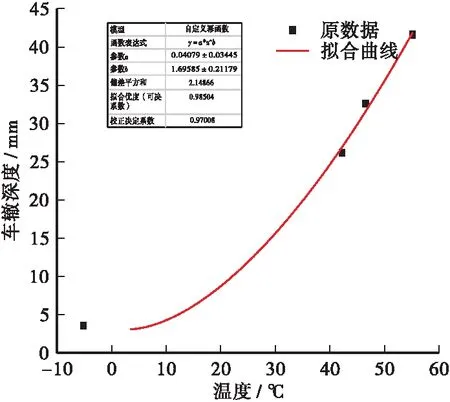
图6 温度对车辙深度的影响Figure 6 Influence of temperature on rut depth

4.3 轴载次数对车辙深度的影响

固定动稳定度、环境温度、荷载压力、车速、面层厚度，探究累计轴载次数对车辙的影响。本研究共设置了8种轴载次数：1 000，5 000，10 000，100 000，250 000，500 000，750 000，1 000 000。计算结果显示，随着轴载次数的增加，车辙持续增长，根据曲线走向采用幂函数对其进行拟合，结果为：R=7.712×10-4×N0.768 89，拟合效果图如图7。

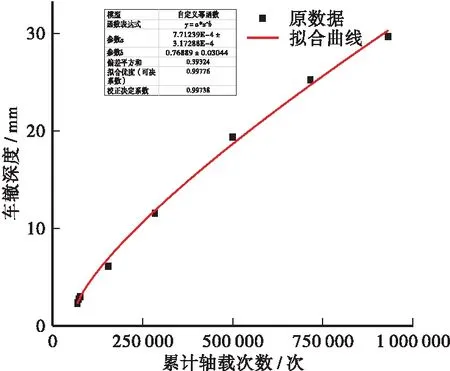
图7 轴载次数对车辙深度的影响Figure 7 Influence of axle load times on rut depth

4.4 荷载压力对车辙深度的影响

将沥青层厚度设为8 cm，车速为60 km/h，研究0.5、0.7、0.9、1.0和1.2 MPa这5种荷载压力作用50万次时车辙发展，计算结果如图8所示。根据数据分布情况，采用线性函数对其进行拟合，表达式为：R=0.409+8.544×P，此时R-squre值为0.999 77，说明拟合效果良好。

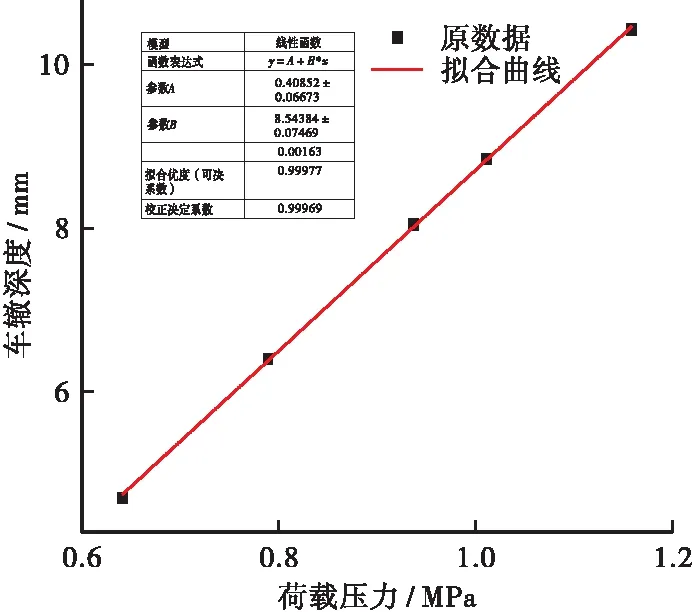
图8 荷载压力对车辙深度的影响Figure 8 Influence of load pressure on rut depth

4.5 面层厚度对车辙深度的影响

在其他影响因素相同的情况下改变沥青层厚度，共设置6种面层厚度：4、6、8、10、12、14 cm。计算结果显示，随着面层厚度的增加，车辙增加，且近似为线性关系，采用一次函数对其进行拟合，结果为：R=0.247+0.751×H，拟合效果图如图9所示。

图9 沥青层厚对车辙深度的影响(单位：mm)Figure 9 Influence of asphalt layer thickness on rut depth(Unit:mm)

4.6 车速对车辙深度的影响

在其他影响因素相同的情况下共设置5种车速：40、50、60、70、80 km/h。计算结果显示，随着车速的增加，车辙减少，采用幂函数对其进行拟合，结果为：R=599.80-0.742×V，拟合效果如图10所示。

图10 车速对车辙深度的影响Figure 10 Influence of vehicle speed on rut depth

由上述各参数对车辙深度的分析可知，荷载压力P、沥青层等效厚度H与车辙深度近似为线性函数关系，而车速V、动稳定度DS、温度T、累计轴次N同车辙深度为幂函数关系。同时由边界条件，即各P和N为0时车辙深度R=0，最终本研究综合考虑各因素作用，构建基于动稳定度的车辙预估模型：R=5.307×10-5×P×H×V-0.8462×DS-0.392 2×N0.881 1×T1.585 5。由此，动稳定度可由荷载工况、面层等效厚度和容许车辙深度反算得到。

5 结论

本研究进行了大量的车辙试验，证明了车辙试验拟合黏弹性参数并用于结构分析的可行性，确定了动稳定指标与黏弹性参数之间的数量关系并用于路面结构分析，最终构建基于动稳定度的多因素车辙预估模型。根据此模型，在一定的荷载条件和路面结构下可根据车辙深度要求确定动稳定度指标。具体结论如下：

a.根据三维应力状态下的Burgers模型蠕变方程拟合车辙试验数据，确定了沥青混合料的黏弹性参数，并将其转化为Prony级数的形式。经有限元计算永久变形和动稳定度后与实测值对比分析，误差分别不超过2%和5%，说明本研究中黏弹性参数获取方法的可行性。

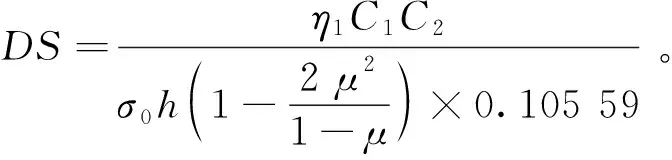
c.本研究基于控制变量的原则分别分析了动稳定度和试验温度、车速、沥青层厚度、荷载压力对车辙深度的影响并最终构建车辙预估模型为：R=5.307×10-5×P×H×V-0.846 2×DS-0.392 2×N0.881 1×T1.585 5，并由此可以在已知设计工况(荷载、结构属性)和容许车辙深度的情况下反算出合适的动稳定度值，达到从荷载和结构特性确定动稳定度的目的。