考虑参数不确定性的红砂岩边坡可靠性分析研究

樊长刚,盛焰正 ,陈双庆

(1.中国市政工程西南设计研究总院有限公司，四川 成都 610081;2.中交第二公路勘察设计研究院有限公司,湖北 武汉 430000；3.中南大学 土木工程学院,湖南 长沙 410018)

1 概述

红砂岩通常指侏罗纪到新近纪的红色、红褐色陆相沉积岩系，约占全国陆地总面积的8.61%[1]，主要呈粒状碎屑结构和泥状胶结结构2种形式，在湖南省俗称“红砂岩”。湖南省湘西地区是红砂岩分布较为集中的地区，由于红砂岩往往分布在亚热带季风气候区 ，热量丰富，春夏降水比较集中，雨量充沛，红砂岩容易在水、氧气、风等因素下风化，极大影响了红砂岩的抗剪强度与其边坡的稳定性[2]。学者们已经开展通过一系列试验研究了红砂岩抗剪强度随环境因素的变化规律，例如陈文杰[3]考虑了红砂岩崩解性，获取了抗剪强度参数随含水率的变化规律。徐志华[4]等开展了干湿循环作用下红砂岩强度劣化特性试验研究，定量分析了干湿循环作用对红砂岩强度力学参数的影响，并提出了基于黏聚力的损伤变量。刘新荣[5]等指出当经历20次干湿循环后，红砂岩的c和φ分别降低58%和34%。上述试验结果为考虑环境影响的边坡稳定性分析和支护设计提供了试验资料，但红砂岩化学成分和结构的复杂性导致红砂岩的性质具有很强的空间差异性，即使在同一地区，其抗剪强度范围区间也分布很广，这对需要明确岩土材料抗剪强度参数的传统边坡稳定性分析带来很大的挑战[6]。实际工程中，勘察设计人员往往在试验数据甚至缺乏试验数据的基础上，根据经验确定某一定值来进行稳定性计算，结果带有较大的主观性。

可靠性理论常用于解决某一系统内的不确定性问题，通过计算边坡的可靠性指标和破坏概率，能够反映边坡的各种不确定影响因素，避免了安全系数使用过程中的绝对化。鉴于此，针对湖南省某公路的风化红砂岩样品进行了抗剪强度参数统计分析，建立了正态分布模型，并开展了利用蒙特卡洛法和罗森布鲁斯法的边坡可靠性分析，研究了支护前后可靠性指标的变化规律，并将可靠性方法分析结果与传统定值方法进行了对比，旨在为今后类似工程的可靠性分析提供参考。

2 边坡可靠性分析理论

2.1 可靠性状态方程与指标

常规的边坡可靠性理论可以参照文献[7]。类似结构可靠性，采用传统的边坡安全系数进行状态判断，即安全系数表示功能函数：

(1)

与上式对应的失效概率为：

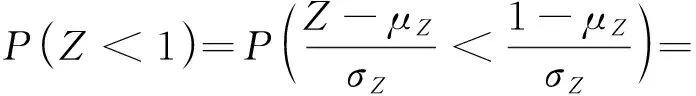
(2)

因此，安全系数功能函数对应的可靠性指标β为：

(3)

式中：μz为功能函数Z的均值；σz表示Z的标准差。边坡可靠性指标与破坏概率的关系如表1所示。

表1 边坡可靠性指标与失效概率的关系Table 1 Relationship between slope reliability index and failure probability性能等级可靠性指标失效概率性能等级可靠性指标失效概率高5.02.871×10-7差2.00.022 75好4.02.169×10-5糟糕1.50.066 81中等以上3.00.001 35危险1.00.158 66中等以下2.50.006 21

2.2 可靠性分析方法

关于边坡可靠性研究已取得了许多成果，可靠性指标的计算方法包括蒙特卡洛法[8]、一次二阶矩法[9]、Rosenblueth法[10]等。

利用蒙特卡洛法(MCS)方法计算边坡失效概率的估计值可表示为[11]：

(4)

式中：xi(i=1，2，…，N)为模拟的随机样本。

蒙特卡洛法[12]又称为统计实验法或随机模拟法，它是一种数值计算方法，其中蒙特卡洛法需要预知各基本变量的分布形式和参数特征，采用蒙特卡洛法计算须随机生成N组随机数，而每组随机数的生成均是以随机变量的分布形式和参数特征为基础的，它只是一种数值计算方法，没有固定的求解公式，只能求得边坡在给定条件和参数下的解，但这恰恰回避了边坡可靠度分析中数学模型的建立困难。

罗森布鲁斯法又称统计矩法，相对蒙特卡洛法，可以大大减少可靠性分析中的计算量，具体理论详见文献[13]和[14]。对于边坡问题，假设模糊参数为c和φ值，则功能函数Z=g(c，φ)。对于每个参数取2个计算点，则有：

Z++=g[(μc+σc)，(μφ+σφ)]

Z+-=g[(μc+σc)，(μφ-σφ)]

Z-+=g[(μc-σc)，(μφ+σφ)]

Z--=g[(μc-σc)，(μφ-σφ)]

(5)

对于普通的可靠性分析，罗森布鲁斯法的一阶矩M1即均值μz，二阶矩M2即方差：

(6)

式中：下标j=1、2、3、4分别代表j=++、+-、-+、--。

P++=P--=0.25(1+ρXY)，P+-=P-+=0.25(1-ρXY)，ρXY为相关系数。

当引入模糊理论时，利用模糊判决中的普通加权平均法，则m个λ水平下考虑模糊随机性的状态函数的一阶原点矩(均值)为：

(7)

二阶矩(方差)为：

(8)

3 实例分析

3.1 工程概况

湖南省湘西某高速公路属低山丘陵地貌，地形起伏较大，山体自然边坡约为10°～40°。边坡大部分呈上下2层的“二元结构”，上部为泥质粉砂岩，岩质软，厚度15～20 m，结构大部分已经破坏，风化裂隙很发育，岩体很破碎，根据《公路工程地质勘察规范》(JTG C20-2011)[15]，属于强风化岩；下部为粉砂岩，结构部分破坏，风化裂隙发育，岩体被切割成岩块，属于中风化岩。二者皆为该高速公路项目的控制性地层，可划于红砂岩的范畴，下文简称“强风化红砂岩”和“中风化红砂岩”,见图1。

图1 代表性岩样

地勘阶段在边坡沿线周边2 km范围内进行了大量钻孔取样，该范围内无大型地质构造，地下水位较深，岩样含水率主要受天然降雨入渗所控制，而受地下水影响可能性不大。参数获取与统计按照《公路土工试验规程》(JTG 3430—2020)[16]、 《公路工程结构可靠性设计统一标准》(JTG 2120—2020)[17]开展。图2为不同位置红砂岩抗剪强度参数的变化情况，可以看出，红砂岩的抗剪强度具有明显的不确定性，这是由矿物成分、含水率等因素的不均匀所造成的，一般而言，石英含量越高，抗剪强度参数越高，而含水率越高，抗剪强度参数则越低。尽管各个样品的抗剪强度参数有较大差异，但整体上均值比较稳定，没有发生漂移，具有正态分布的特征，风化程度越高，不确定性更明显。

对上述结果进行整理，得到抗剪强度参数正态分布曲线如图3所示。从图3可以看出，岩石抗剪强度参数c、φ值均近似服从正态分布，强风化红砂岩参数的不确定性更大。

(a) 黏聚力

(b) 内摩擦角

(a) c的参数分布

(b) φ的参数分布

用于可靠性分析的案例边坡为四级坡，高度约29 m。边坡内汇水面较小，地表水不发育，地下水贫乏，水文地质条件简单，对边坡稳定性影响小。一级、二坡比为1∶0.75，三、四级坡比为1∶1。一至三级坡采用锚杆防护，锚杆长9 m；四级坡采用植草防护。在支护前，坡体发生了2次小规模失稳破坏。图4为该边坡支护前后的照片。

(a) 支护前

(b) 支护后

3.2 蒙特卡洛法计算结果分析

在蒙特卡洛法基础上，利用简化Bishop条分搜索滑面并计算功能函数值(即安全系数)，共进行了800次抽样计算。天然未支护状态和采用锚杆支护状态的计算结果如图5所示。

从图5可以看出，支护前后最危险滑面均从坡顶开始发育，在第一级坡的坡面中上部出露，是否支护对滑面的形态影响不大。图6为2种工况下安全系数的分布概率直方图，可知边坡的安全系数基本上符合正态分布。对图中安全系数小于1的计算次数进行统计，边坡在未支护情况下安全系数小于

(a) 未支护

(b) 已支护

1的次数为180次，即边坡失效破坏概率为22.6%，说明该边坡在不采取任何支护措施的情况下，发生破坏的概率比较大，这与强风化红砂岩抗剪强度较低有关；而边坡采取锚杆支护措施后，安全系数小于1的次数为38次，即边坡的失效破坏概率为4.8% ，说明锚杆加固后边坡稳定性显著提高。

(a) 未支护

(b) 已支护

参照罗文强[18]等的报道，从失效概率角度出发，可以将边坡稳定性分为5个等级，见表2。

表2 基于失效概率的边坡稳定性等级Table 2 Slope stability grade based on failure probability稳定性描述失效概率/%稳定等级不稳定>90 1稳定性差60～902欠稳定20～603基本稳定5～204稳定<5 5

根据之前的分析，支护前边坡失效概率Pf=22. 6%，处于欠稳定状态，这与现场出现失稳的情况相符，进行支护后，边坡失效概率Pf=4.8%，表明支护后边坡处于稳定状态，体现了进行锚杆支护的工程意义。

3.3 罗森布鲁斯法计算结果分析

考虑到计算量，仅采用罗森布鲁斯法计算支护后边坡的可靠性。表3为采用罗森布鲁斯法时的计算参数。下标1代表强风化红砂岩，下标2代表中风化红砂岩，例如c1-代表强风化红砂岩c值在小于统计期望值一侧模糊估计值。

表3 计算参数Table 3 Parameters for Calculation隶属度不确定性参数c1-/kPac1+/kPaφ1-/(°)φ1+/(°)c2-/kPac2+/kPaφ2-/(°)φ2+/(°)0.1011.230.88.2225.58385224.2635.740.2011.930.18.8424.9638.551.524.6735.330.3012.629.49.4624.34395125.0834.920.4013.328.710.0823.7239.550.525.4934.510.50142810.723.1405025.934.10.6014.727.311.3222.4840.549.526.3133.690.7015.426.611.9421.86414926.7233.280.8016.125.912.5621.2441.548.527.1332.870.9016.825.213.1820.62424827.5432.46

不同隶属度下安全系数和可靠性指标的变化规律如图7所示。可以看出，可靠性指标与安全系数同时随着参数隶属度的增加而提高。根据式(3)、式(7)和式(8)，边坡的可靠性指标β=1.70，失效概率为Pf=6.3%。由于罗森布鲁斯法考虑了岩土参数的模糊随机性，因此计算出的失效概率是大于蒙特卡洛法的。

图7 不同隶属度下的安全系数均值与可靠性指标Figure 7 Safety factor mean and reliability index under different memberships

3.4 与传统方法对比

为了进一步对比可靠性分析法与传统定值安全系数法的区别，选择了3名工作经验在5 a以上的公路勘察设计人员，其根据工作经验分别给出了强风化红砂岩和中风化红砂岩抗剪强度参数经验值，并利用简化Bishop法进行经验值参数下的稳定性计算，结果见表4。

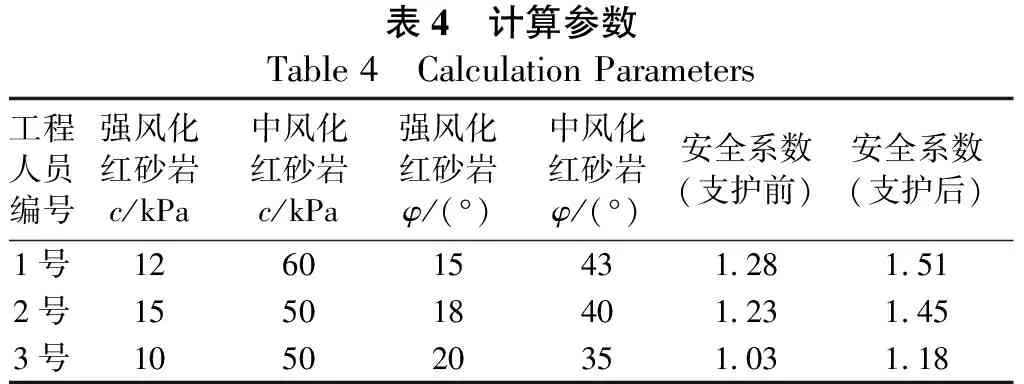
表4 计算参数Table 4 Calculation Parameters 工程人员编号强风化红砂岩c/kPa中风化红砂岩c/kPa强风化红砂岩φ/(°)中风化红砂岩φ/(°)安全系数(支护前)安全系数(支护后)1号126015431.281.512号155018401.231.453号105020351.031.18

根据《公路路基设计规范》JTG D30—2015[19]，对于高速公路正常工况，安全系数为1.20～1.30视为稳定。受到矿物成分、含水率等因素影响，现场红砂岩抗剪强度具有明显的不确定性，采用传统确定性安全系数法时，由于个人主观经验原因，1号和2号工程人员估计的计算参数使得未支护前边坡处于稳定状态，与现场情况有所偏差，导致边坡设计支护手段不足而出现失稳破坏危险。而3号工程人员的计算结果偏保守，即支护之后安全系数仍然未达稳定要求，可能造成支护措施的过度加强而引起新的工程成本开支。 同时可以看出，采用传统安全系数法计算时，支护前边坡的安全系数都大于1，但实际边坡出现了失稳破坏的现象，这从传统安全系数法理论上是难以解释的。而可靠性理论认为任何边坡的失稳破坏都是概率问题，只是支护前失效概率高，支护后失效概率低，从而为参数不确定条件下的边坡稳定性分析提供了更科学的理论支撑。

4 结论

本文以湘西某红砂岩区高速公路边坡建设为例，在考虑岩土参数空间不确定性的前提下，利用蒙特卡洛法、罗森布鲁斯法进行了边坡可靠性分析，得到如下结论：

a.根据勘察统计数据，红砂岩的抗剪强度具有明显的不确定性，这是由矿物成分、含水率等因素的不均匀所造成的，一般而言，石英含量越高，抗剪强度参数越高，而含水率越高，抗剪强度参数则越低。

b.根据蒙特卡洛法计算结果，支护前红砂岩边坡失效概率Pf=22.6%，处于欠稳定状态，这与现场出现失稳破坏情况相符；进行支护后，边坡失效概率Pf=4.6%，表明支护后边坡处于稳定状态，失稳概率很小。

c.根据罗森布鲁斯法计算结果，支护后红砂岩边坡的可靠性指标β=1.70，失效概率为Pf=6.3%，相对蒙特卡洛法，采用罗森布鲁斯法计算得出失效概率更大，偏于保守。

d.可靠性分析理论为参数不确定条件下的边坡稳定性分析提供了更科学的理论支撑，可避免工程人员因为个人经验对岩土参数做出过高或过低的估计，从而导致设计支护强度不足。尤其在大数据时代，可以利用超高次数计算来获取高精度的可靠度计算结果，具有十分广阔的应用前景。