钢-UHPC组合结构的栓钉连接件疲劳性能分析

孙艳华,谭本坤，雷顺成，魏 维

(1.湖南联智科技股份有限公司， 湖南 长沙 410200； 2.长沙理工大学，湖南 长沙 410114;3.湖南省交通科学研究院有限公司， 湖南 长沙 410015)

1 概述

钢-混组合结构因其优越的性能和便于施工的特点，广泛应用于桥梁施工建设之中。近年来，随着超高性能混凝土材料(UHPC)的提出，为解决正交异性钢桥面板铺装层极易损伤和钢构件疲劳开裂的问题提供了新思路[1]，通过在钢桥面上浇筑UHPC材料使2种结构形成整体，大大提高了原始结构的局部刚度，成为一种新型的钢-UHPC轻型组合桥梁结构[2]，逐渐成为一种被认可的有效解决方案。而栓钉连接件作为连接混凝土材料和钢梁的关键构件，其疲劳性能是研究人员关注的重点[3-4]。

与普通混凝土-钢组合构件的结构形式类似，钢-UHPC组合构件通过栓钉连接件将2种材料连接，区别在于后者的UHPC层厚度较小，采用的栓钉通常直径为10～16 mm且高度为24～40 mm的短栓钉[5]。对于栓钉的疲劳性能评估，传统S-N曲线方法主要是通过试验数据拟合栓钉所承受的名义剪切应力幅值与疲劳作用次数之间的关系[6-8];然而实际工程中，栓钉不仅承受剪切应力，尤其对于钢-UHPC组合结构中的短栓钉，还承受一定的拉力，属于多轴复合受力模式。因此,传统方法对不同种类和应用场景下栓钉的疲劳性能评估存在一定局限性，通过试验拟合得到的公式难以适用于不同类型和不同材料中的栓钉，LEE[9]等通过对直径在30 mm以上的大直径栓钉进行疲劳试验，发现其疲劳寿命低于现有规范预测值；XU[10]等通过疲劳试验发现橡胶套筒会降低栓钉的剪切刚度，从而导致疲劳寿命降低；曹君辉[11]对钢-UHPC组合结构中的短栓钉进行推出试验，发现其相较于普通混凝土中的栓钉有稍优越的疲劳性能。随着有限元的发展，断裂力学方法在钢桥的疲劳性能评估得到了较好的应用[12]，王宇航[13]等基于断裂力学对组合梁中的栓钉进行了疲劳性能分析，石广玉[14]等通过Schwartz-Neuman交替法对栓钉进行了三维疲劳扩展计算，研究均较好地预测了短栓钉的疲劳寿命，为栓钉的疲劳性能分析方法提供了新的途径，然而目前研究均未考虑栓钉疲劳裂纹萌生寿命的因素，同时基于断裂力学方法对于UHPC中栓钉的研究仍有待深入。

鉴于以上研究的不足，本文基于通过有限元方法，建立带有栓钉焊趾细节的精细化推出试验有限元模型，对UHPC中栓钉的受力性能进行了分析。在此基础上，通过SWT参数方法，对栓钉的疲劳最不利位置和对应的临界平面进行了计算，结合断裂力学方法累加得到了栓钉的疲劳寿命值，最后基于有限元方法，提出了UHPC中短栓钉疲劳寿命预测公式。

2 推出试验模型

本文所研究的钢-UHPC组合结构的栓钉连接件疲劳性能问题，实际上是钢桥面高强混凝土钢筋网片铺装层抗剪性能问题。目前对于栓钉连接件的静疲劳性能研究主要通过推出试验实现，该方法相较于梁式试验较为经济便捷，各国规范也给出了推出试验中标准试件的设计要求，本文中的推出试验模型参照了文献[11]中的推出试验，该文献研究所依据的标准为Eurocode 4规范[6]。具体采用板厚50 mm的UHPC混凝土，厚度为12 mm的工字型钢，间距为50 mm×55 mm的φ10普通钢筋，工字型钢每侧布置4个直径和高度分别为13 mm和35mm的短栓钉，横竖向间距分别为110 mm和200 mm。其中钢材的弹性模量均为2.06×105，栓钉与工字型钢的屈服强度和极限强度分别为345、430 MPa，钢筋的屈服强度和极限强度分别为335、400 MPa，钢材泊松比为0.3，UHPC材料泊松比为0.2。试验的具体布置和尺寸如图1所示。

图1 试件布置及几何尺寸

3 有限元模型的建立

3.1 模型建立

推出试件有限元模型由UHPC板、短栓钉、工字型钢板、加载板和构造钢筋组成，有限元模型通过大型有限元软件Abaqus进行建模，模型考虑了材料本构的非线性与材料之间的接触关系。考虑计算便利，根据模型所受约束与荷载的对称性，仅取1/4试件进行精细化有限元模型的建立，并在对称平面上施加对称约束，在工字型钢板上方建立加载钢板并通过施加位移荷载模拟推出试验的加载，疲劳性能分析时通过在钢板顶面施加均布压力以模拟疲劳荷载上下幅值。工字型钢板、栓钉与UHPC之间采用表面接触，摩擦系数设置为0.4。在模型底部设置参考点，并与底板绑定以输出加载历程。

有限元模型中UHPC板、工字型钢板和栓钉构件均采用三维实体单元C8DR模拟，普通钢筋单元采用桁架单元T3D2模拟通常栓钉的疲劳破坏是栓钉焊接时存在初始缺陷等原因导致的，同时有研究表明栓钉焊环对其抗剪切承载能力提供了一部分积极作用[11]，因此有限元模型对栓钉焊趾进行了精细化建模，具体尺寸参照相关规范[15]，考虑栓钉焊接细节的钢-UHPC组合推出试验精细化有限元模型如图2所示，图中的整体模型为对称显示，实际仅建立1/4模型。

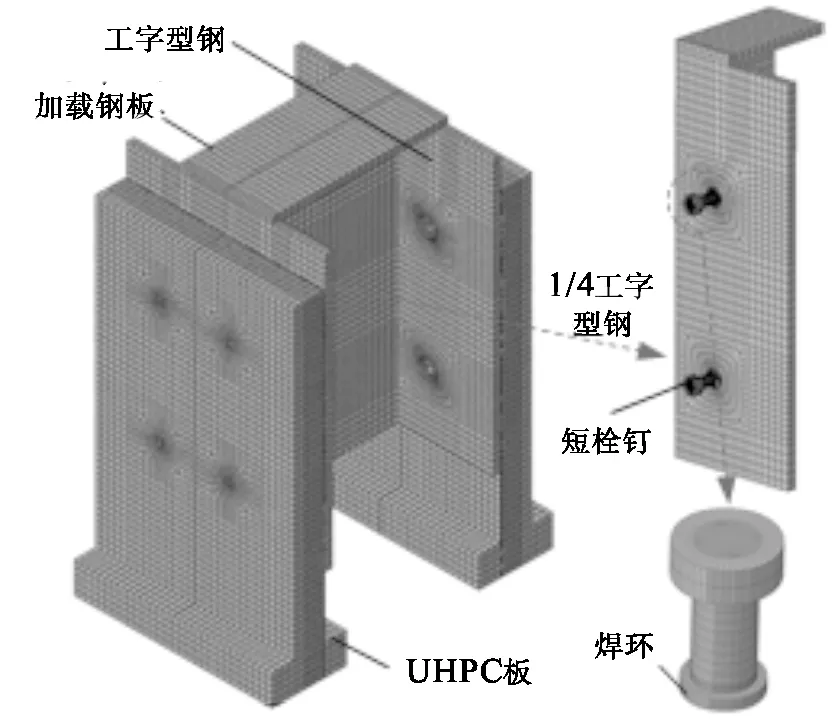
图2 钢-UHPC组合推出试验精细化有限元模型Figure 2 Refined FE model of steel-UHPC composite structure push-out test

由于试验过程中工字型钢板，以及钢筋均处于弹性受力状态，因此假定钢板和钢筋为理想弹性材料，采用双折线模型，而栓钉经过了一个显著的屈服阶段，因此采用三折线弹塑性本构进行建模，即初始为弹性受力，然后硬化，最后发展至塑性，相关参数参照文献[11]中试验所得结果。根据推出试验结果，靠近栓钉根部的UHPC板的混凝土存在明显的破坏，因此此处采用混凝土损伤塑性模型模拟UHPC的开裂和破坏，参照文献[16]-文献[18]中所提出的UHPC受拉和受压应力应变曲线，如图3和图4中所示。具体参数按照文献中试验所得结果进行设置，计算公式如式(1)、式(2)所示， 基于能量等价原理通过式(3)定义UHPC受拉、受压的损伤因子D。

(1)

(2)

(3)

式中：εt0为受拉峰值处应变；ft为应变硬化阶段的平均应力；εtp为受拉极限应变；lc为试件测量的引伸标距；wp是裂缝宽度参数；p是轴拉性能试验拟合所得到的参数；fc为抗压强度；ξ为受压应变值与受压峰值应变比值；ε0为受压峰值应变。

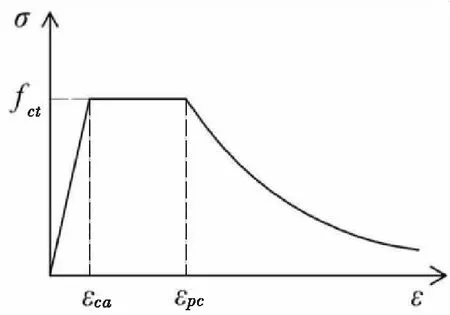
图3 UHPC受拉应力-应变曲线Figure 3 Tensile stress-strain curve of UHPC

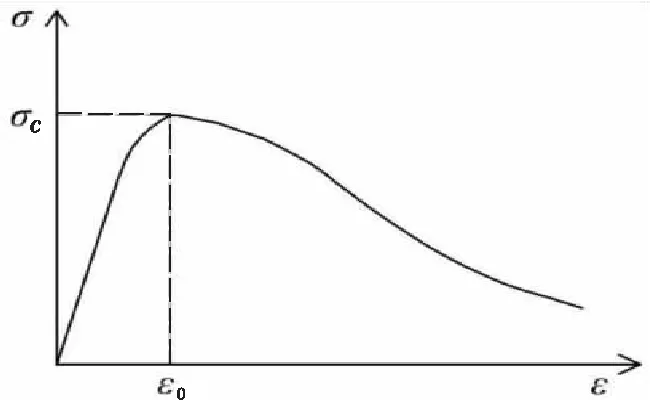
图4 UHPC受压应力-应变曲线Figure 4 Compression stress-strain curve of UHPC

3.2 计算结果验证与分析

文献[11]对相同构造的3个推出试件SAT-1～SAT-3进行了试验，并且记录了栓钉的滑移情况和极限承载能力，本文通过有限元模型计算得到的荷载-滑移曲线与试验结果对比如图5所示，有限元计算所得的各构件应力云图如图6所示，图中结果仅显示1/4有限元模型。根据2图可以看出，通过建立栓钉焊接细节的有限元模型计算得到的结果与实测荷载-滑移曲线基本一致，并且与试件SAT-2的结果最为接近，并且曲线能够反映钢-UHPC组合结构推出试验中栓钉的2个阶段，即加载初期栓钉的荷载-滑移曲线基本呈线性变化，栓钉屈服后界面滑移的速度逐渐加快，最终达到极限强度栓钉发生剪切破坏。

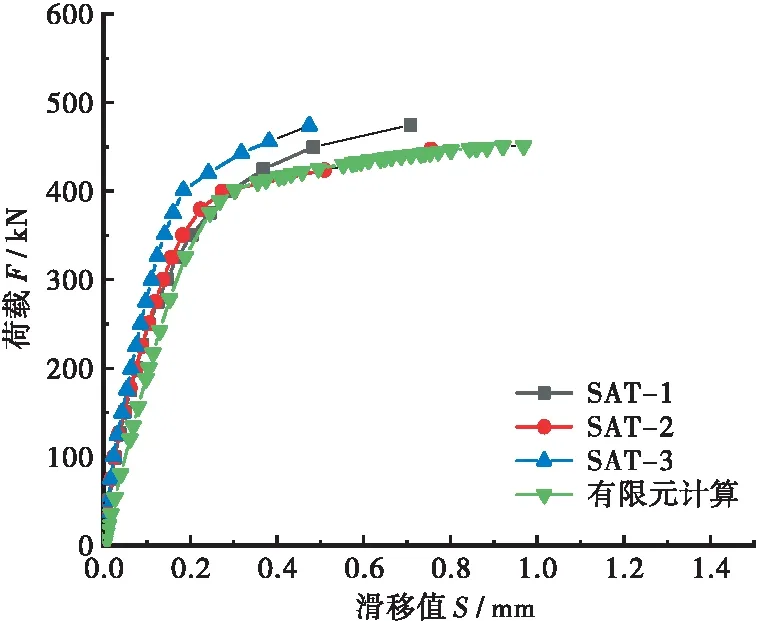
图5 栓钉荷载滑移曲线对比Figure 5 Comparison of load slip curves of studs

(a)UHPC受拉损伤分布

(b)UHPC受压损伤分布

(c)栓钉最大主应力云图

4 疲劳寿命计算

4.1 疲劳损伤参数分析

断裂力学方法将疲劳裂纹的扩展过程分为初始裂纹的萌生阶段和疲劳裂纹稳定扩展阶段，以及最终的裂纹不稳定扩展阶段，其中不稳定扩展阶段发生较快，对于总体的疲劳寿命来说可以不计算在内，因此本文通过计算裂纹萌生寿命Ninit,及稳定扩展寿命Nprop的总和来对栓钉的疲劳寿命N进行计算。首先采用临界平面法计算裂纹萌生寿命Ninit，再基于线弹性断裂力学计算稳定扩展寿命Nprop。

栓钉剪力连接件在UHPC板中承受剪切荷载时，同时受剪力、弯矩和轴向荷载作用，其处于多轴应力-应变状态，因此采用多轴疲劳寿命预测的临界平面方法对栓钉的萌生寿命Ninit和最不利平面方向进行计算，通过定义SWT参数对多轴应力问题进行分析，参数定义如式(4)所示，其中乘积为应变能的一种表征，认为某点的SWT参数值达到最大值的方向即为临界平面方向，疲劳裂纹在该方向进行扩展。

(4)

式中：Δε和σmax分别为每个疲劳荷载周期的法向应变幅值和最大法向应力。在临界平面，该损伤参数达到最大值。

疲劳寿命与SWT参数相关，可通过式(5)对疲劳裂纹萌生寿命进行计算[19]。由于目前缺少栓钉材料疲劳扩展速率试验的相关参数，参照文献[10]中的设定，式中参数σ′f和ε′f分别采用350 MPa和0.071 5，b和c分别取-0.07和-0.4。

(5)

式中：b和c分别是疲劳强度指数和疲劳延性指数；σ′f和ε′f分别是疲劳强度系数和疲劳延性系数。

通过线弹性断裂力学方法对栓钉的稳定扩展疲劳寿命Nprop进行计算，计算基于Paris式(6)，通过应力强度因子K和疲劳扩展速率参数C、m进行计算，C和m的取值参照文献[10]分别为4.47×10-14和3.0，初始裂纹a0一般通过无损检测探伤技术进行确定，此处栓钉的初始裂纹a0取2mm[13]，应力强度因子K的计算如式(7)所示。

(6)

(7)

式中：F为疲劳裂纹几何形态修正系数，本文按1.12进行计算；σ为不带初始裂纹结构所受应力；a0为初始疲劳裂纹深度；af为疲劳失效时的裂纹深度。

栓钉在承受疲劳荷载作用时，其抗剪切能力主要通过栓钉杆身的抗剪切面积决定，在出现疲劳裂纹前，抗剪切面积为栓钉直径d所对应的圆截面面积A，随着疲劳荷载作用裂纹逐渐扩展，栓钉的抗剪切面积不断减少，最终减少至所承受疲劳荷载幅值上限Pmax对应的极限抗剪切面积Af时发生疲劳破坏，因此，疲劳失效时的疲劳裂纹深度af可由式(8)计算：

(8)

(9)

式中：fu为栓钉材料的抗拉极限强度。

如前述，在进行疲劳寿命计算分析时，需要先确定最不利位置，进而计算其最大SWT参数，及其对应的临界平面方向。即首先计算得出钢-UHPC推出试件中短栓钉的应力应变场，初步确定疲劳荷载下的最不利区域，对最不利区域单元进行SWT参数评估，再通过坐标转换矩阵得到图7所示的任意平面的法向应力应变分量，坐标转换的公式如式(10)所示。图7中转换前的坐标系为xyz，坐标转换后可得到新的坐标系x′y′z′[20]，在此基础上即可计算出最易出现疲劳裂纹的最不利位置,及其所对应的临界平面，最后根据公式(5)对栓钉的疲劳萌生寿命进行计算[11]。

图7 任意平面位置示意图Figure 7 Schematic diagram of any plane position

2τyznynz+2τxznxnz

2γyznynz+2γxznxnz

(10)

式(10)中的σ和ε是转换平面后的法向应力应变，nx、ny、nz分别为转换后坐标系与转换前坐标系之间的夹角方向的余弦，计算公式如下：

nx=cosθsinφ

ny=sinθsinφ

nz=cosφ

(11)

式中：θ是x轴与平面法向量在xy平面投影的夹角；φ是平面法向量与z轴的夹角。

根据试验结果，栓钉疲劳试验所观察到的破坏模式主要包括2种：第1种的疲劳裂纹源出现在栓钉与钢板焊接位置处，随着疲劳荷载的作用，裂纹逐渐在钢板上延伸并形成一个较小的凹面；第2种是栓钉杆身与焊趾相交位置出现疲劳裂纹，基本沿横向扩展并逐渐贯穿栓钉横截面，直至达到栓钉的抗剪切极限[11]。由栓钉连接件在剪切荷载下的最大主应力云图可知，栓钉杆身与焊趾相交位置的应力最为不利，初步判定其为疲劳裂纹发生位置，这与试验中所观察到的第2种试验结果是一致的。由此以N1试件为例，对栓钉杆身-焊趾交界位置进行SWT参数计算分析，计算时夹角取值间距按照10°进行取值。得到如图8所示的SWT参数结果，最大时最不利平面所对应的夹角θ与φ分别为90°与20°，后续分析中判定疲劳裂纹由此处

图8 栓钉杆身-焊趾交界位置的SWT参数图Figure 8 SWT parameter diagram of stud shank - weld collar interface

发展，SWT参数值为74 460，临界平面相对于全局平面的法向量为(-0.000 272， 0.342， 0.940)，计算得到法向应变幅值Δε为915με，最大法向应力σmax为166.8 MPa，Δσ法向应力幅值为135.1 MPa。

4.2 疲劳寿命分析

根据计算得到的SWT参数值和法向应力幅值Δσ，即可通过式 (5)和式 (6)对试件N1～ N5中栓钉的萌生裂纹寿命Ninit和稳定扩展寿命Nprop分别进行计算，试件N1 ～ N5的计算结果Nf与文献[11]中的试验结果Ne对比如表1所示，计算logNe/ logNf值的范围为0.98～1.04，可以看出二者有较好的相关性，进一步计算得出本文计算结果与试验结果之间的相关性系数为0.995 5，说明本文通过综合考虑栓钉疲劳萌生寿命和稳定扩展寿命来进行疲劳寿命预测的方法是可行的。

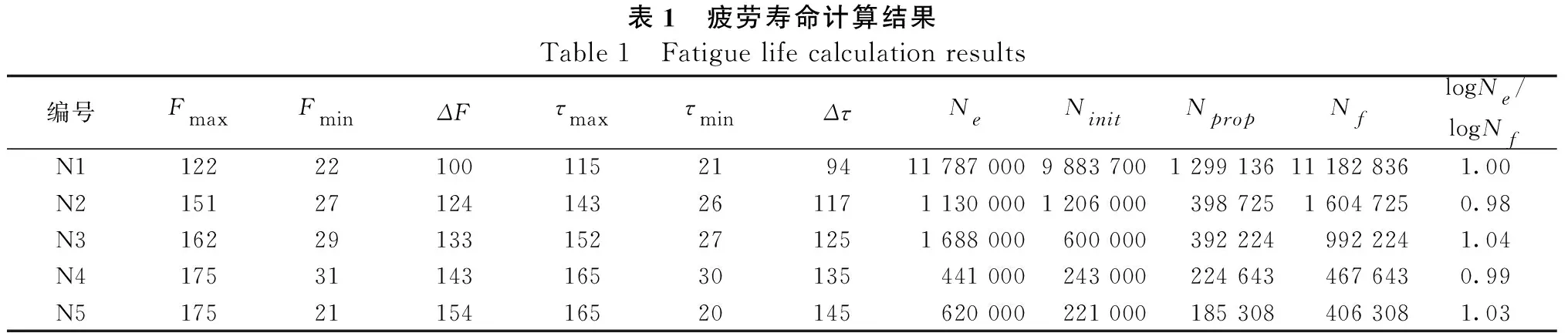
表1 疲劳寿命计算结果Table 1 Fatigue life calculation results编号FmaxFminΔFτmaxτminΔτNeNinitNpropNflogNe/ logNfN112222100115219411 787 0009 883 7001 299 13611 182 8361.00 N215127124143261171 130 0001 206 000398 7251 604 7250.98 N316229133152271251 688 000600 000392 224992 2241.04 N41753114316530135441 000243 000224 643467 6430.99 N51752115416520145620 000221 000185 308406 3081.03

对于不同疲劳荷载幅值下的作用次数关系，可以通过数据拟合的方式进行统计分析，建立出钢-UHPC组合结构中短栓钉的名义应力S-N曲线，现行规范也是通过此方式指导设计的[6-8]。名义应力S-N曲线的计算公式如式(12)，表2给出了公式中的参数值，表2中还给出了文献根据试验数据给出的参数值，为保证预测的安全性，该值是按照95%的存活率给出的。

mlogΔτ+logN=C

(12)

式中：N是疲劳荷载作用次数；Δτ是栓钉所受名义剪切应力幅值；C、m是试验数据拟合得到的参数。

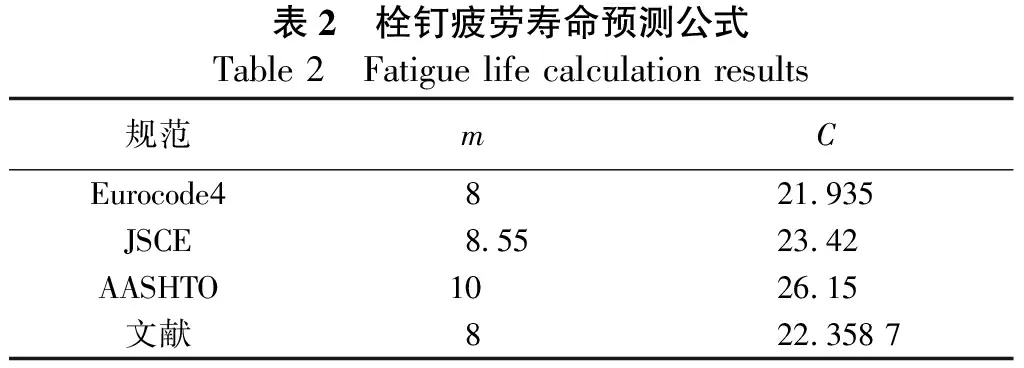
表2 栓钉疲劳寿命预测公式Table 2 Fatigue life calculation results规范mCEurocode4821.935JSCE8.5523.42AASHTO1026.15文献822.358 7

将文献[11]中的试验结果,及其拟合得到的曲线公式绘出，如图9所示，同时在图9也给出了表2中规范的曲线，以及本文计算得到的结果作为比较。可以看到UHPC中短栓钉的疲劳寿命相较于普通混凝土组合构件推出试验所得出的预测曲线计算出的寿命值更大，以试件N1为例，疲劳应力幅值为94 MPa，试验所得疲劳寿命值为1 178.7万次，规范Eurocode 4计算结果为141.2万次，这是UHPC较大的弹性模量，及约束作用所导致的。此处将材料设置为文献[17]中弹性模量为43 000 MPa，抗压强度为170.9 MPa的UHPC，计算得到的栓钉最不利处SWT损伤值结果如图10所示。由图10可以知不同强度的SWT损伤图分布基本一致，最大为71 810，相较于本文试验材料中的栓钉损伤值要小，其对应的疲劳萌生寿命值为1 259.0万次，稳定扩展寿命值为89.2万次，可见不同强度的混凝土中栓钉的疲劳性能存在一定差异。

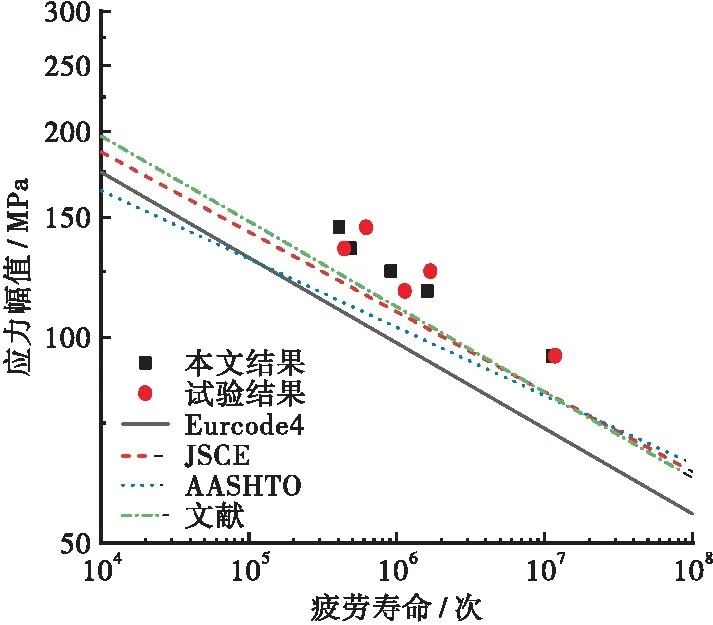
图9 UHPC中短栓钉的名义应力S-N曲线图Figure 9 Nominal stress S-N curve of short stud in UHPC

通过表1中数据可以发现在整个疲劳寿命中初始疲劳裂纹萌生寿命占了相当大部分的比例，最大可达93%，对于受疲劳应力幅值较小的栓钉连接件，疲劳裂纹萌生寿命所占比例更大，这意味着在实际结构中栓钉的服役过程中，相当一部分时间处于初始疲劳裂纹萌生的阶段，而当疲劳裂纹深度达到稳步扩展阶段时，疲劳破坏的发生是相对较快的，因此对于钢-UHPC组合结构，栓钉连接件焊接细节的疲劳裂纹检测尤为重要，同时疲劳应力幅值是决定栓钉连接件疲劳裂纹扩展寿命的关键参数，因此本文参照上述拟合公式，提出基于有限元计算结果的栓钉疲劳寿命预测公式(13)。

8.131 logΔτ+logN=23.089

(13)

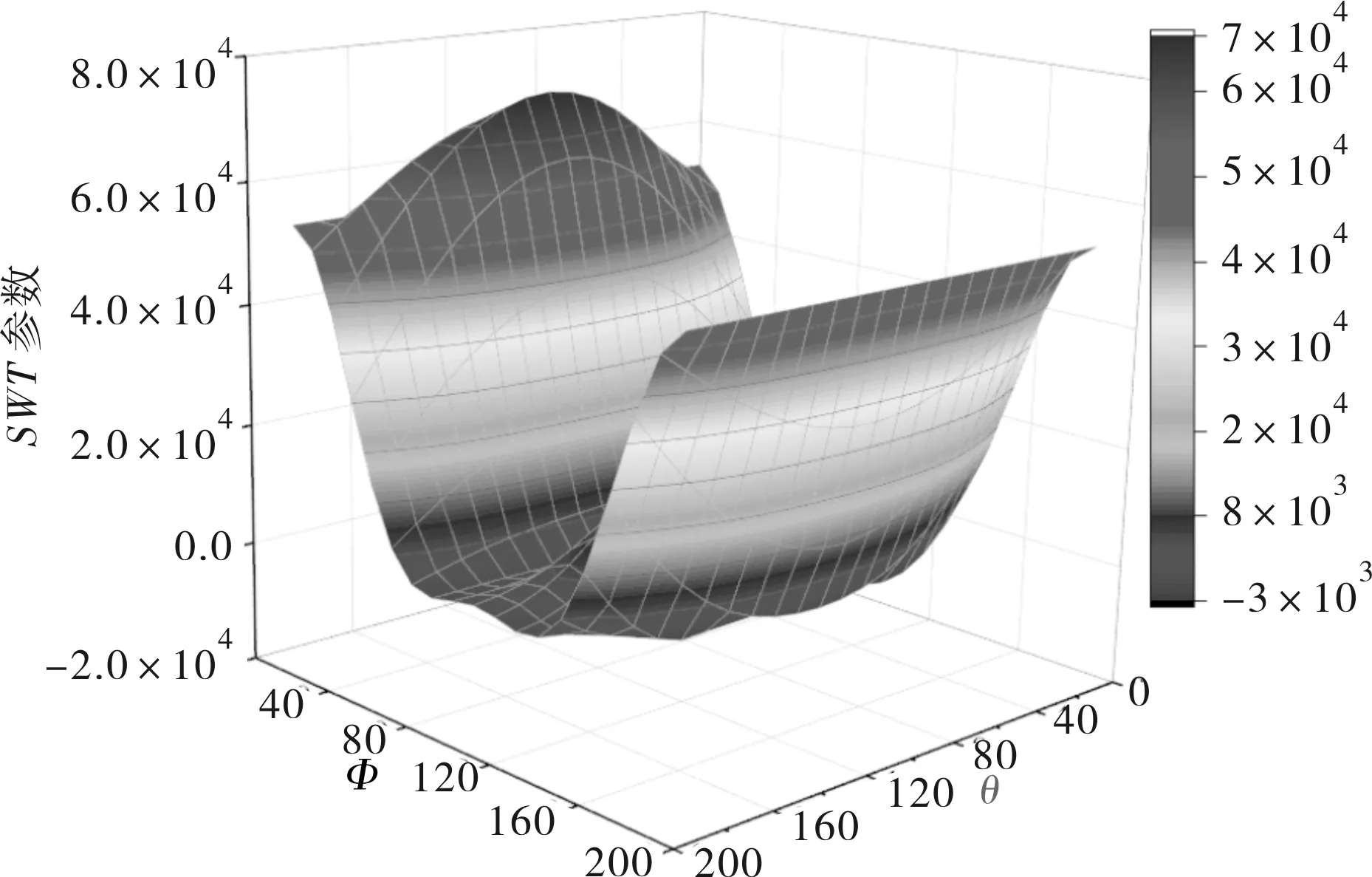
图10 不同强度UHPC中栓钉的SWT参数图Figure 10 SWT parameter diagram of pins in UHPC with different strength

5 结论

本文建立考虑栓钉焊接细节的精细化有限元模型，通过多轴疲劳临界平面法和断裂力学方法分别计算出栓钉的疲劳裂纹萌生寿命和稳定扩展疲劳寿命，对UHPC中的短栓钉疲劳性能进行了分析，研究结论如下：

a.通过定义推出试验构件材料的非线性本构，同时考虑栓钉焊趾细节，能够很好地模拟栓钉的荷载滑移曲线和抗剪强度，同时通过有限元方法能够直观地反映试验所观察到的最不利位置。

b.所预测的疲劳裂纹萌生位置位于栓钉杆身与焊趾细节交界处，疲劳寿命预测结果与试验基本一致，并利用有限元方法，提出了钢-UHPC组合构件中栓钉连接件的疲劳寿命预测公式，本文方法能够较好地用于UHPC中短栓钉的疲劳性能评估。

c.UHPC较高的弹性模量对栓钉有更强的约束作用，使得其变形相较于普通混凝土中的栓钉较小，不同强度中的剪切连接件的疲劳特性存在一定差异。

d.在整个疲劳破坏过程中疲劳裂纹萌生寿命所占比例较大，最大可达90%以上，疲劳应力幅值是决定栓钉连接件疲劳裂纹扩展寿命的关键参数。