基于漂移流动模型的水平井岩屑床高度瞬态计算新方法

孙晓峰 姚 笛 孙士慧 纪国栋 于福锐 孙铭浩 赵元喆 陶 亮

1.“提高油气采收率”教育部重点实验室·东北石油大学 2.东北石油大学三亚海洋油气研究院3.中国石油集团工程技术研究院有限公司

0 引言

目前，水平井已是油气资源开采的常用井型，但钻井过程中岩屑极易在造斜段和水平段沉降形成岩屑床，从而引发钻具高摩阻，高扭矩、钻头托压、卡钻等一系列问题[1-6]。因此，有必要深入研究大斜度与水平井段的运移规律，建立瞬态岩屑运移模型对岩屑成床与运移规律进行描述，从而准确预测井眼环空内岩屑的分布情况。

现有国内外学者所建立的岩屑瞬态运移模型主要以岩屑床高度预测分层模型为主，包括两层岩屑运移模型与三层岩屑运移模型[7-13]。Martins等[14]以两层岩屑稳态运移模型为基础，首次建立了时间相关的两层岩屑瞬态模型。Wang等[15]等提出了基于SETS方法的三层瞬态模型求解方法。Zhang等[16]基于环空固液两相流流型建立了一种动态岩屑床分层预测模型，模型的层数可由流型确定。Guo等[17]将三层稳态模型与两层非稳态模型相结合，建立了三层瞬态运移模型。Fallah等[18]提出了基于漂移模型的两层岩屑瞬态模型。

就目前的研究来看，岩屑分层运移模型虽然可以计算岩屑瞬态沉积高度，但模型求解速度慢，耗费计算资源，且仅在没有扰动时适用。在大斜度与水平井段钻进过程中，钻杆旋转、震动与起下均是流动中的大扰动，钻井液与岩屑的固液两相流存在沙丘流、分层流、分散悬浮等多种流型，此时岩屑分层模型并不适用。因此，本文不对环空中的固液两相流动进行区域划分，将环空中的钻井液与岩屑视为一个整体，仅考虑相间的滑移作用，应用漂移流动模型建立一维环空固液两相流动瞬态计算模型，采用有限体积法对井眼环空空间进行离散，离散后应用投影法进行求解。解得各项流动参数后再通过井斜角、岩屑床孔隙度等判别条件计算大斜度井段岩屑床的高度。以期为水平井的岩屑床清除提供指导，提高水平井井眼清洁效率。

1 环空固液两相流瞬态流动模型

在水平井钻进过程中，岩屑以一恒定的体积浓度进入环空中。流入环空的岩屑与钻井液混合，形成混合流体不断向井口运移[19]，如图1所示。笔者使用漂移流动模型对环空钻井液—岩屑的两相流流动进行模拟，漂移流动模型最早由Zuber等[20]提出，模型将混合流动的两相流体看作一种流体，忽略相间的质量传递与能量传递，考虑相间的滑移速度关系[21-22]。笔者应用Walton[23]所建立的固液两相漂移速度关系，构建井眼环空固液两相流瞬态流动模型。

图1 井筒环空固液两相流动示意图

1.1 基本假设

环空固液两相流瞬态流动模型的基本假设如下：①固液两相在环空中的流动是一维的，各相流动参数保存在井筒网格节点，且在同一时间步时间内流动参数值保持恒定。②模型不考虑环空中的温度变化，且在流动过程中钻井液与岩屑均不可压缩，岩屑颗粒均为均匀球型颗粒，具有相同的粒径。③岩屑颗粒在小斜度井段（井斜角小于等于30°）与直井段中始终保持均匀分散状态，在井斜角大于30°的井段中中会沉积形成岩屑床层。④假设模型计算得到的固相岩屑全部沉积形成岩屑床，则可通过岩屑床孔隙度将岩屑床体积分数转化为无因次岩屑床高度，本文中假设岩屑床孔隙度为52%。

1.2 控制方程

钻井液与岩屑的连续性方程分别为：

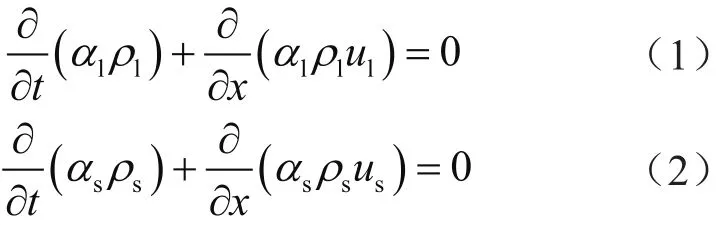
钻井液与岩屑的混合动量方程为：

式中αl、αs分别表示液相、固相体积分数，无量纲；ρl、ρs分别表示液相、固相密度，kg/m3；ul、us分别表示液相、固相速度，m/s；p表示压力，Pa；q表示源项。源项考虑了质量力与钻井液流变性等外界因素对流动的影响，包含重力项与阻力项两部分，其表达式为：

式中Fg、Fw分别表示重力分量、阻力分量，Pa/m；θ表示井斜角，（°）；g表示重力加速度，m/s2；di、do分别表示钻杆外径、井眼内径，m；f表示范宁摩擦系数，无量纲；ρm表示固液相混合密度，kg/m3；um表示固液相混合速度，m/s。

固液相混合密度与混合速度的表达式分别为：

固相体积分数与液相体积分数之间的关系满足：

1.3 漂移速度模型

考虑岩屑与钻井液之间的滑移关系，固相与液相间的漂移速度关系为：

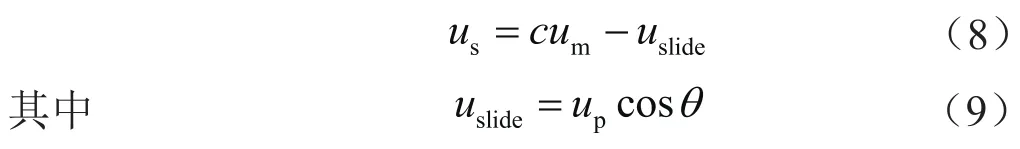
式中uslide表示相间滑移速度，m/s；up表示岩屑沉降速度，m/s；c表示相间分布系数，无量纲。相间分布系数c表示速度与浓度分布的不均匀度，受井斜角、钻杆转速、钻井液密度、流型等多种因素影响，通常由实验获得。

岩屑在幂律流体中的沉降速度up表达式为[24]：

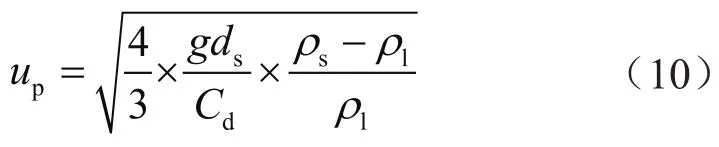
其中阻力系数的表达式为：

颗粒雷诺数与沉降速度的关系为：

式中ds表示岩屑颗粒的当量直径，m；Cd表示岩屑颗粒在钻井液中的阻力系数，无量纲；Res表示岩屑的颗粒雷诺数，无量纲。

2 模型求解方法

2.1 离散格式

由于水平井井筒的轴向尺寸远大于径向尺寸，不考虑管柱偏心问题，可以将三维空间井筒简化为沿井筒轴向方向的一维空间，并对井筒一维空间均匀划分。由于本文所研究的钻井液与岩屑的固液两相流是标准的不可压缩流动，为避免出现奇偶失联型压力场影响计算精度，选用基于交错网格的有限体积法对井筒空间进行离散，将井筒空间分为一系列控制体，对控制体单元进行质量与动量守恒分析，离散后的井筒网格如图2所示，交错网格将标量储存在控制体中心，速度参数储存在控制体边界。边界处的固相体积分数与液相体积分数可通过插值获得。

图2 井筒环空网格离散示意图

连续性方程的时间推进可直接采用显格式进行时间离散，n+1时刻固相连续性方程与液相连续性方程的离散格式分别为：

对于混合动量方程，由于钻井液与岩屑的固液两相流为不可压缩流动，无法通过时间推进进行求解压力项。因此本文采用投影法求解混合动量方程的压力泊松方程，从而得到n+1时刻各相速度与压力的值。

2.2 投影方法

投影法最早由Chorin提出[25]，用于求解不可压缩的纳维斯托克斯方程。该方法通过计算中间时间步得到压力泊松方程，再对压力泊松方程求解即可得到新时刻的压力值。相比Simple类或人工压缩性方法求解不可压缩流动[26-27]，投影法无需反复内迭代进行求解，极大地提高了计算效率。使用投影法对混合动量方程进行求解，首先对式（3）进行时间离散，离散化后的表达式为：

将式（16）分裂为式（17）、（18）两部分，将时间推进分为预算步、压力修正步和最终步三部分进行。预算步与的压力修正步的表达式分别为：

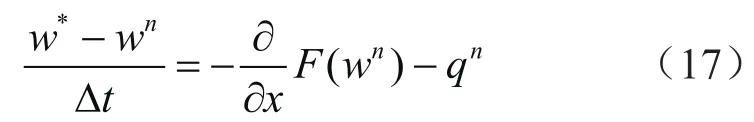
首先计算预算步，对式（17）进行空间离散，可以得到中间时间步的计算表达式：

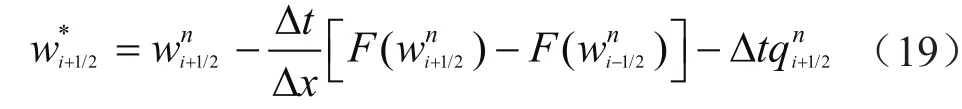
接下来计算压力修正步，由于环空中的固液两相皆为不可压缩流体，流体的密度随流动的变化率较低，可以认为n+1时刻守恒变量的散度为0。对式（18）求散度，可以得到混合动量方程的一维压力泊松方程：

对上式进行空间离散化，得到离散的压力泊松方程：

重复式（19）～（21）可以得到整个井筒空间各节点的压力泊松方程，将其化为矩阵的形式：

使用超松弛法对离散的压力泊松方程进行求解，解出n+1时刻的井筒各节点处的压力值pn+1后，即可进行最终步的计算，对式（18）进行空间离散，并将预算步与压力修正步计算得到w*与pn+1代入离散后的式（18），即可计算得到wn+1。得到wn+1后还需进行守恒变量的还原求解n+1时刻的固相速度与液相速度。

将式（13）与式（14）进行变换，得到n+1时刻的液相体积分数与固相体积分数：

对固液两相的漂移速度方程进行离散，得到n+1时刻的固相速度与液相速度关系式：

将式（23）、（24）、（25）代入式wn+1，进行变量还原，通量与液相速度之间的关系为：

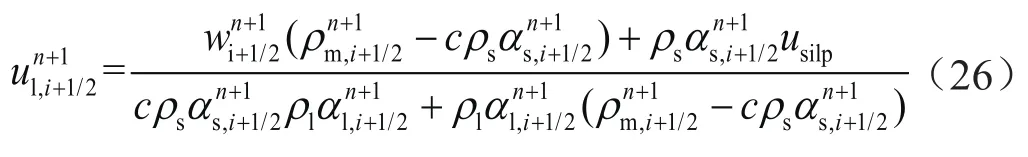
得到n+1时刻井筒的液相速度分布与固相速度分布。至此n+1时刻井筒的压力分布与速度分布全部求解完成，将该时刻的所有参数作为基础，计算下一时刻井筒内各点参数值直至计算完毕。

2.3 模型计算步骤

模型的具体计算步骤如图3所示。

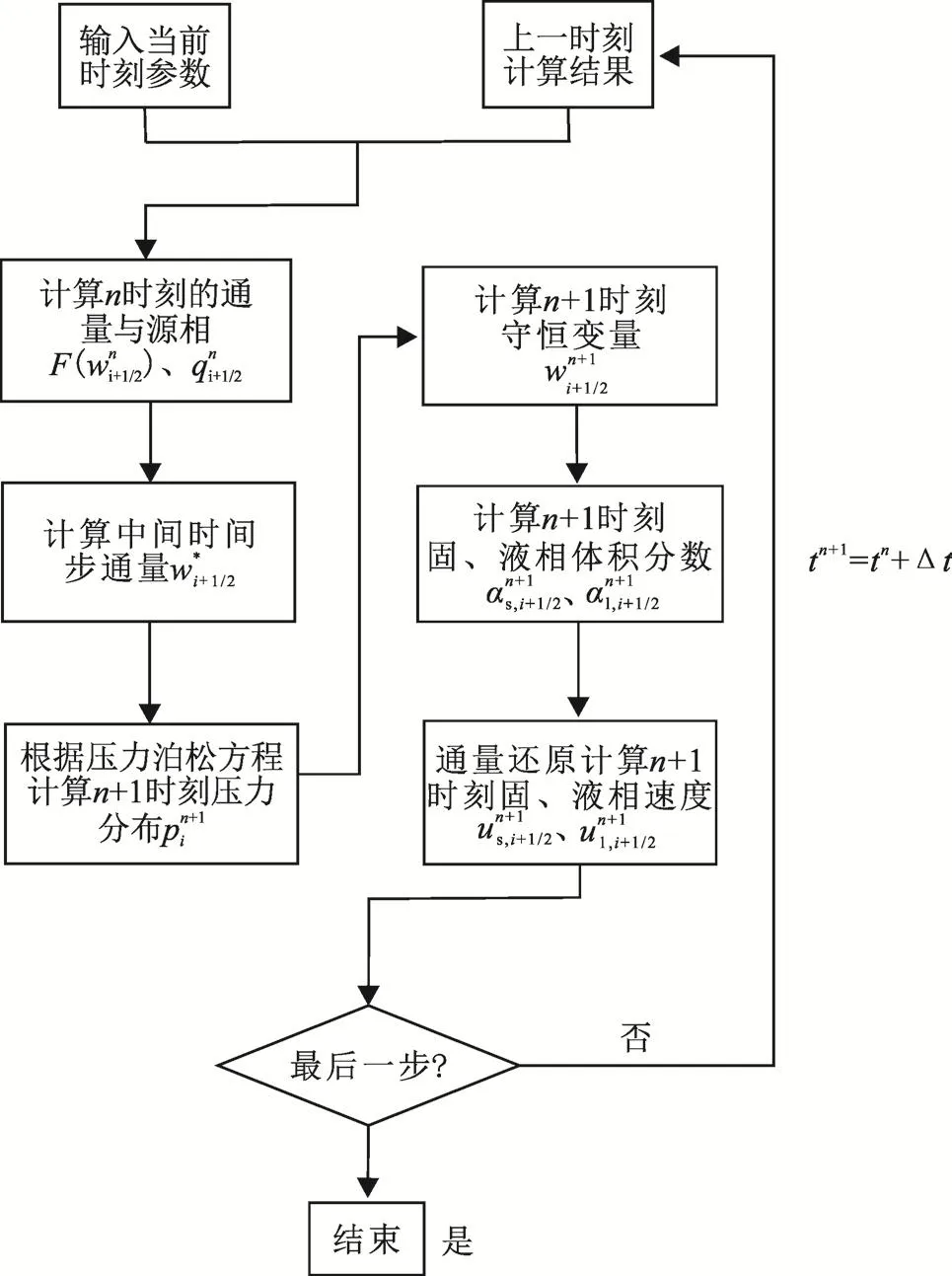
图3 算法计算步骤示意图

①首先输入钻井液排量、钻进速度、井口压力等基本参数，结合已知n时刻井眼环空内各参数的值，计算n+1时刻边界值。②根据n时刻的通量与源项，利用预算步计算中间时刻的守恒变量w*。③对压力修正步求散度，得到混合动量方程的压力泊松方程。对压力泊松方程进行离散，将其化为矩阵形式。使用超松弛法对矩阵进行迭代求解，得到n+1时刻井筒的压力分布pn+1。④根据n时刻的速度与体积分数，计算n+1时刻的固相体积分数与液相体积分数。将各相体积分数与计算得到的结果代入最终步，求解n+1时刻的固相速度与液相速度。

重复步骤①～④，即可计算得到全部时刻井筒内全部节点的固液相体积分数、固液速度与压力值。

3 模型算例分析与验证

为验证算法的准确性与实用性，本节将应用所建立的模型模拟钻井过程中岩屑在井眼环空中的瞬态运移规律，如图4所示，并对数值模拟所计算结果进行分析验证。

图4 不同时刻环空岩屑体积分数及环空压耗分布情况图

3.1 模型算例分析

某小井眼水平井水平段长250 m，井眼内径127 mm，钻杆外径76 mm，井斜角90°，岩屑密度2.60 g/cm3，岩屑粒径34 mm，钻井液密度1.18 g/cm3，钻井液有效黏度50 mPa·s。环空排量选取8 L/s、10 L/s、12 L/s三种工况，机械钻速30 m/h。将井筒划分为100个网格，单位网格长度2.5 m，模拟计算总时长t=6 000 s，时间步长1 s。模拟开始后向入口处不断注入岩屑，直至井筒中岩屑体积分数保持恒定时模拟结束。

在模拟开始0～100 s时岩屑未进入环空，此时水平段环空为纯钻井液，环空中的压力呈线性分布，液相速度保持恒定。自100 s后开始注入岩屑，图4-a为110 s时环空中的岩屑体积分数分布，此时岩屑刚流入环空，少量随钻井液向出口运移，绝大部分沉积于入口，且不同环空排量下的岩屑沉积量差异较大。由于此时三种排量下的钻井参数一致，仅环空排量不同，且岩屑进入量较小，因此环空压力与未进入岩屑时基本一致，环空压耗主要为钻井液流动所产生阻力，如图4-b所示。

模拟时间达到280 s时，此时岩屑已大量进入环空。如图4-c所示，高排量下岩屑随钻井液快速流动，自钻头处沿环空逐渐形成稳定岩屑床，岩屑体积分数保持恒定。低排量下岩屑仍然在不断聚集，岩屑床仍处于发育阶段，尚未完全形成，岩屑体积分数沿环空不断降低，且环空排量越低岩屑聚集速度越慢。此时的环空压耗与井底压力明显升高，环空压耗由岩屑运移与钻井液流动所产生阻力组成，岩屑体积分数较高的井段环空压耗大幅增加，如图4-d所示。

图4-e、f为模拟时间达到1 300 s时环空岩屑分布情况与压耗分布情况，此时高排量下的环空岩屑体积分数已趋于稳定，固液两相的流动状态不再随时间发生变化。低排量下的岩屑也开始在入口处形成稳定岩屑床，并沿环空向出口不断运移。此时低排量下的井底压力已高于高排量下的井底压力，这是因为岩屑运移所产生阻力远高于钻井液流动阻力，环空岩屑体积分数成为影响环空压耗的主要因素。

模拟时间达到4 000 s，此时排量为10 L/s、12 L/s的环空中已形成稳定岩屑床，环空岩屑体积分数保持不变，排量为8 L/s的环空中部分井段的岩屑体积分数仍未稳定，直至模拟达到5 400 s时才形成稳定岩屑床，此时三种工况下的井底压力与环空压耗也趋于稳定。

图5-a、b为排量为8 L/s时环空固、液相速度的分布情况。排量一定的情况下岩屑运移速度主要受岩屑体积分数影响，岩屑体积分数越大则流动产生的阻力越大，运移速度越慢。且岩屑进入环空后不断聚集并沉积形成岩屑床，导致钻井液的流道减小，由于岩屑运移速度较低且密度高于钻井液密度，因此岩屑体积分数越高的井段液相速度越高。

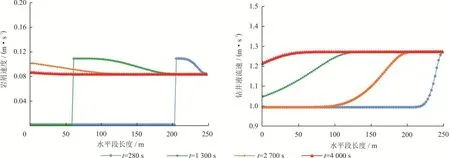
图5 不同时刻环空固、液相速度分布情况图

图6为不同环空排量下形成岩屑床时间，环空排量较低时岩屑运移速度也较小，从钻头处运移至出口的时间更长。且由于低排量时钻井液流动速度缓慢，导致大量岩屑聚集，环空中的岩屑体积分数增高，岩屑产生堆积效应，极大地降低了岩屑运移速度。因此低排量下形成稳定岩屑床所需时间要远远大于高排量下形成稳定岩屑床所需时间，岩屑的堆积效应在长水平段钻进过程中尤为明显，随着水平段长度的增加，岩屑堆积导致井下摩阻呈指数性增长，严重影响了水平段的安全钻进。利用本文所建立模型，可以计算得到形成稳定岩屑床所需时间，从而合理设计停钻循环时间或改变泵排量与钻杆转速，在岩屑床影响正常钻进前及时进行清除，预防高摩阻所产生的卡钻、钻具磨损等问题，提升大位移井钻井过程中的井眼清洁效率[28-30]。

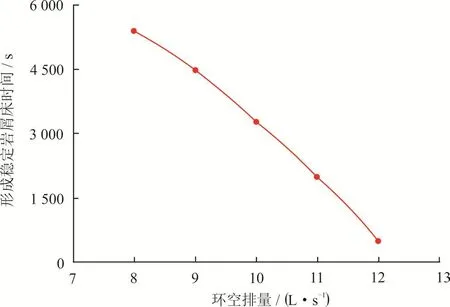
图6 不同环空排量下岩屑床形成时间图

3.2 模型验证

为验证本文所建立模型的准确性，将模型计算结果与稳态岩屑床高度计算模型[31]进行了对比。取本文算例中的钻井参数进行计算，结果如图7所示。

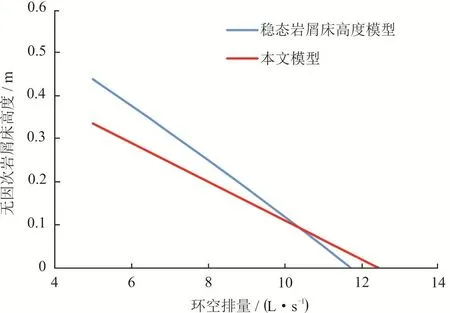
图7 模型对比验证图

由图7可知，在环空排量较大时，本文模型与稳态模型计算结果较为接近，在环空排量较小时本文模型所计算岩屑床高度低于稳态模型，由于稳态模型所预测岩屑床高度略高于室内实验的实测值1%～8%，因此可以认为本文所建立模型可以基本满足实际工况中对岩屑床高度进行预测的需求。

4 结论

1）提出了一种一维瞬态模拟算法，根据钻井携屑实际工程特点将环空固液两相流动简化为一维，采用基于离散网格有限体积法与投影方法，对模型进行离散化求解，得到了岩屑床高度在井筒中的变化规律。通过与稳态岩屑床高度模型进行对照，验证了本文模型与计算公式的准确性。

2）应用投影方法对固液混相动量守恒的纳维斯托克斯方程进行数值求解，首先利用中间时间步求解压力泊松方程得到环空中的压力分布，再将连续性方程与漂移流动关系代入混合动量方程，求解得到固相速度、液相速度、固相体积分数与液相体积分数。算法将压力与速度解耦分别进行求解，且无需反复进行内迭代计算，极大地提升了计算效率。

3）所建立模型可用于研究岩屑床在环空中的形成规律，从而实现水平井环空岩屑床高度的实时监测，且模型求解效率较高，可以满足长水平井段岩屑床计算和监测的需求。模型计算结果可以为水平井的岩屑床高效清除与卡钻事故风险预测提供一定的理论指导。